高速列车轴箱轴承典型故障特征的数值仿真分析

周瑾，方聪聪，张洁，周伟，关煜彬，张港丽

(1.中南大学 交通运输工程学院，轨道交通安全教育部重点实验室，湖南 长沙，410075；2.中南大学 轨道交通安全关键技术国际合作联合实验室，湖南 长沙，410075；3.中南大学 轨道交通列车安全保障技术国家地方联合工程研究中心，湖南 长沙，410075)

高速列车的轴箱轴承肩负着承重、传递各方向的作用力和降低运行阻力的任务，其对高速列车的运行品质、运行安全性、动力学性能起着重要作用。内部元件的动力学特性为高速列车轴箱轴承的服役性能之一，深刻了解缺陷条件下轴箱轴承的动力学响应，对于轴箱轴承的故障诊断与运行维护具有重要的参考价值。STRIBECK[1]基于HERTZ 接触理论，对球轴承静力学进行了分析，推导出球的最大载荷与轴承径向载荷之间的关系。WALTERS[2]提出了滚动轴承的完全动力学模型。随着计算机技术的发展，有限元方法被广泛应用于滚动轴承动力学分析。 TADINA 等[3]将LAGRANGE运动方程与FEM方法相结合研究了滚动球轴承启动期间由于滚道表面的缺陷及外圈局部变形引起的振动。随着计算机技术的发展，计算多体动力学方法也逐渐成为分析复杂机械系统动力学问题的主要工具。SAKAGUCHI等[4]利用商业软件MSC.ADAMS 建立了六自由度的圆锥滚子轴承动力学仿真模型。近年来，国内很多研究者使用商业软件建立了轴承的拟动力学/动力学分析模型[5-10]，郑秋梅等[11]利用ANSYS 建立了高速列车齿轮箱轴承的静力学模型，分析了齿轮箱轴承平均接触应力与温度场分布。目前，人们对现有轨道交通轴承的故障诊断与寿命预测技术研究较多[12]，如ZHANG等[13-14]提出了一种基于小波变换的车轮-轴承系统复合故障检测方法，但关于高速列车轴箱轴承的故障动力学模型研究很少。人们对故障诊断信号的考虑较单一，没有充分考虑高速列车运行工况下轴箱轴承高速重载对滚子动力学特性的影响，对摩擦打滑与保持架效应对故障特征的影响的研究也较少，为此，本文作者对高速列车轴箱轴承典型故障特征进行数值仿真分析。

1 高速列车轴箱轴承完全动力学模型

1.1 轴箱轴承动力学模型建模

国内高速列车的轴箱轴承多使用双列圆锥滚子轴承，本文以CRH5型动车组采用的SKF双列圆锥滚子轴承BT2-8545 AD 为例，采用MSC Adams建立高速列车轴箱轴承完全动力学模型。双列圆锥滚子轴承的具体参数如表1所示。

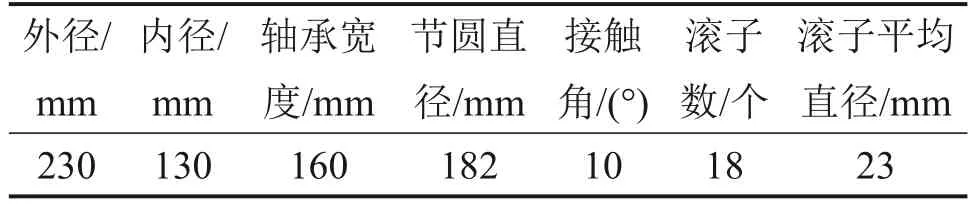
表 1 双列圆锥滚子轴承主要参数Table 1 Main parameters of double row tapered roller bearings

高速列车在运行过程中，轴箱轴承除常规重力载荷外，还受到空气动力学效应气动载荷与轨道激励高频振动冲击载荷，轴承各元件之间的相互作用十分复杂。轴箱轴承外圈与轴箱箱体、内圈与列车车轴均为过盈配合。列车运行时，外圈与轴箱箱体无相对运行，内圈随着列车车轴运行，滚子与保持架在空间内运动。轴箱轴承各元件运行形式复杂，为了减小计算复杂度，基于轴箱轴承各元件动力学特性，进行如下假设：

1)轴箱轴承外圈无自由度(完全固定)，内圈具有5 个运动自由度(给予绕x轴方向的转动驱动)，保持架具有6个运动自由度，滚子具有6个运动自由度(如图1所示)。

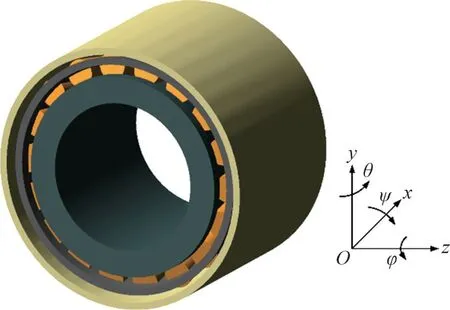
图1 高速列车轴箱轴承动力学仿真模型Fig.1 Dynamic model of high-speed train axle box bearing

2)轴承内圈与隔圈刚性连接，没有相对运动。

3)轴承各元件形状规则，质量分布均匀，质心与几何中心重合。

4)轴承各元件接触刚度较大，不产生柔性变形，轴承元件间的接触变形量极小，不影响轴承元件几何形状。

5)轴承加工和安装无误差。

6)忽略圆锥滚子母线修型，滚子母线为直线。

圆锥滚子轴承中各零件间的相互作用(包括滚子与滚道间的相互作用、滚子与保持架兜孔间的相互作用、保持架挡边与内外圈的相互作用)十分复杂。轴承各元件间的接触力不断变化，这使得轴承元件的运动变得更加复杂。

Adams中对于接触力计算有2种方法，分别为补偿法和冲击函数法，本文采用冲击函数法进行计算。轴箱轴承接触模型如图2所示，2 个元件发生接触的接触力可以用弹簧阻尼系统来表示，2个物体之间的弹性接触力计算式为

式中：K为接触刚度；δ为两物体间接触点法线方向的穿透距离；为δ在穿透方向上的一阶导数，即速度；e为碰撞指数，反映材料非线性程度；C为阻尼系数。轴承接触模型如图2所示，模型接触参数如表2所示[15]。

表 2 接触参数[15]Table 2 Contact parameters[15]

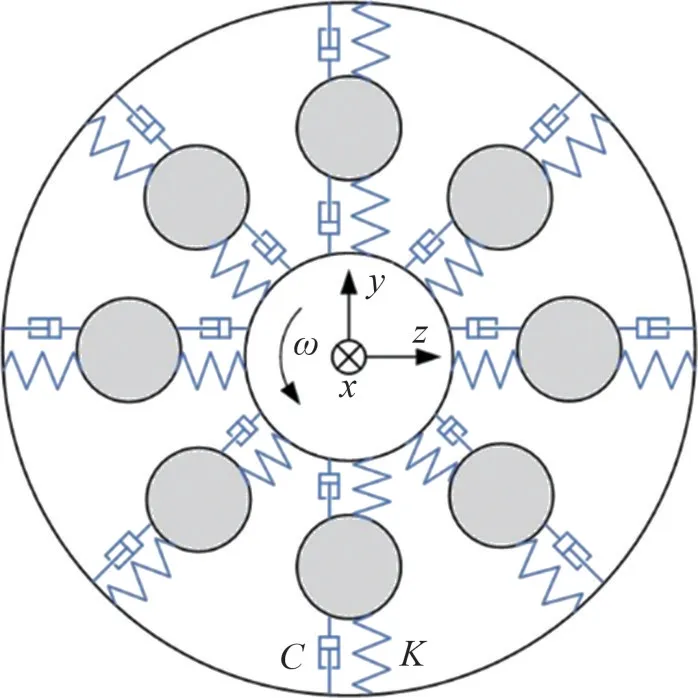
图2 轴箱轴承接触模型Fig.2 Contact model of axle box bearing

1.2 轴箱轴承动力学模型验证

CRH5 型高速列车的车轴最大轴质量为17 t，最高运营速度为250 km/h，新车轮径为890 mm，每轴成对安装双列圆锥滚子轴承，因此，高速列车在运行工况时，轴箱轴承的内圈转速为1 490 r/min，内圈的垂向载荷为85 kN。本文通过对比仿真模型与理论计算的速度与接触力检验该动力学模型是否符合数值理论计算结果。

理论上，不考虑滚子与内外圈滚道之间的打滑，保持架理论角速度为

式中：ωc为保持架理论转速；ωi为内圈转速；ωo为外圈转速；Dw为滚子直径；Dpw为轴承节圆直径；α为轴承接触角。

图3所示为高速列车运行工况下轴承左保持架(x轴坐标为负)与右保持架(x轴坐标为正)的角速度与理论角速度对比。由式(2)可知，保持架理论转速为652.3 r/min，即角速度为68.3 rad/s。由图3可知：左右保持架角速度趋近于保持架理论角速度，左右保持架角速度相对误差均约为1.73%，造成误差的原因可能是滚子与内外滚道打滑所致。图4所示为高速列车运行工况下滚子与轴承内(外)圈滚道的接触力在x轴、y轴和z轴方向上分量之和的变化曲线。滚子与内(外)圈接触力在y方向的分量之和在85 kN(-85 kN)附近波动；滚子与内(外)圈接触力在z轴与x轴方向的分量之和在0 N 附近波动。这均与轴承载荷工况下的结果相符，说明该动力学模型是合理的。

图3 保持架角速度对比Fig.3 Comparison of cage angular velocity

图4 滚子与滚道接触力之和Fig.4 Sum of contact forces between rollers and races

2 高速列车轴箱轴承典型故障动力学分析

接触疲劳及振动冲击引起的表面磨损、擦伤及保持架破损等逐渐为滚动轴承失效的主要形式之一[16]。本文研究轴承外圈剥离、内圈剥离、滚子剥离以及保持架破损等典型故障并分析其故障特征。为了简化故障模型，突出故障特征，将故障缺陷设置较大。将多种轴箱轴承典型故障表示在1张示意图内，见图5(实际模型中为单个缺陷类型)，具体缺陷尺寸如表3所示，其中，保持架某一兜孔贯穿断裂，外圈、内圈、滚子缺陷在轴向方向(x轴)均为单侧贯穿缺陷。

图5 轴箱轴承典型故障Fig.5 Typical defects of axle box bearings

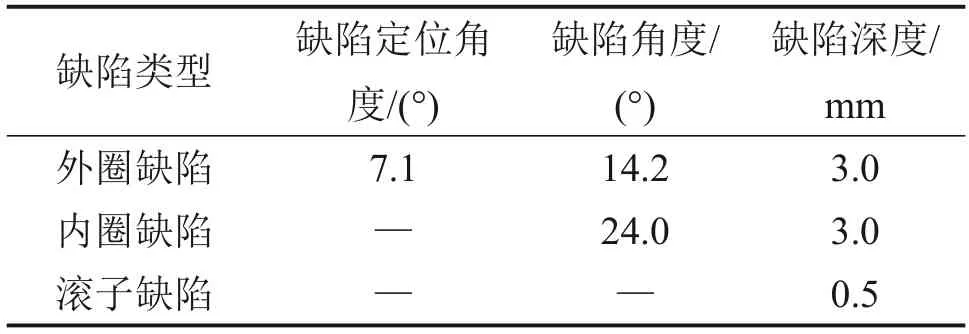
表 3 轴承缺陷尺寸Table 3 Dimensional parameters of bearing defects

2.1 滚子的动力学综合分析

由图5可知：滚子运行轨迹可以分为4个运动区间，以右手定则确定正方向，z轴正方向为0 相位，根据滚子质心绕x轴转动的夹角θr定义为滚子的相位角。根据相位角[0°～90°)，[90°～180°)，[180°～270°)和[270°～360°]可以将滚子运动区间分为B，C，D和A区间，其中，A区间可以平分为A1和A2区间，滚子在4个区间循环运动，A1，B，C，D和A2各区间交接点分别为Pa1b，Pbc，Pcd，Pda2和Pa2a1点。B区间与C区间为承载区间，D区间与A区间为非承载区间。无缺陷轴承在高速列车运行工况下轴承左右两侧某滚子动力学分析结果见图6。从图6 可见：滚子在Pa2a1点进入A1区间角速度逐渐增大，到达Pa1b点后进入B承载区间；当滚子承载从0逐渐增大到最大承载力(在Pbc点)时，角速度稍增大；当滚子从Pbc点进入C区间时，承载逐渐减小，角速度稍减小；当滚子到达Pcd点时，承载为零；当滚子进入D非承载区间时，角速度减小；当滚子进入到A2非承载区间时，角速度进一步减小。从以上分析可知：当滚子接近承载区时，角速度增大，并在承载区与承载力呈正相关关系；当滚子远离承载区时，角速度减小。

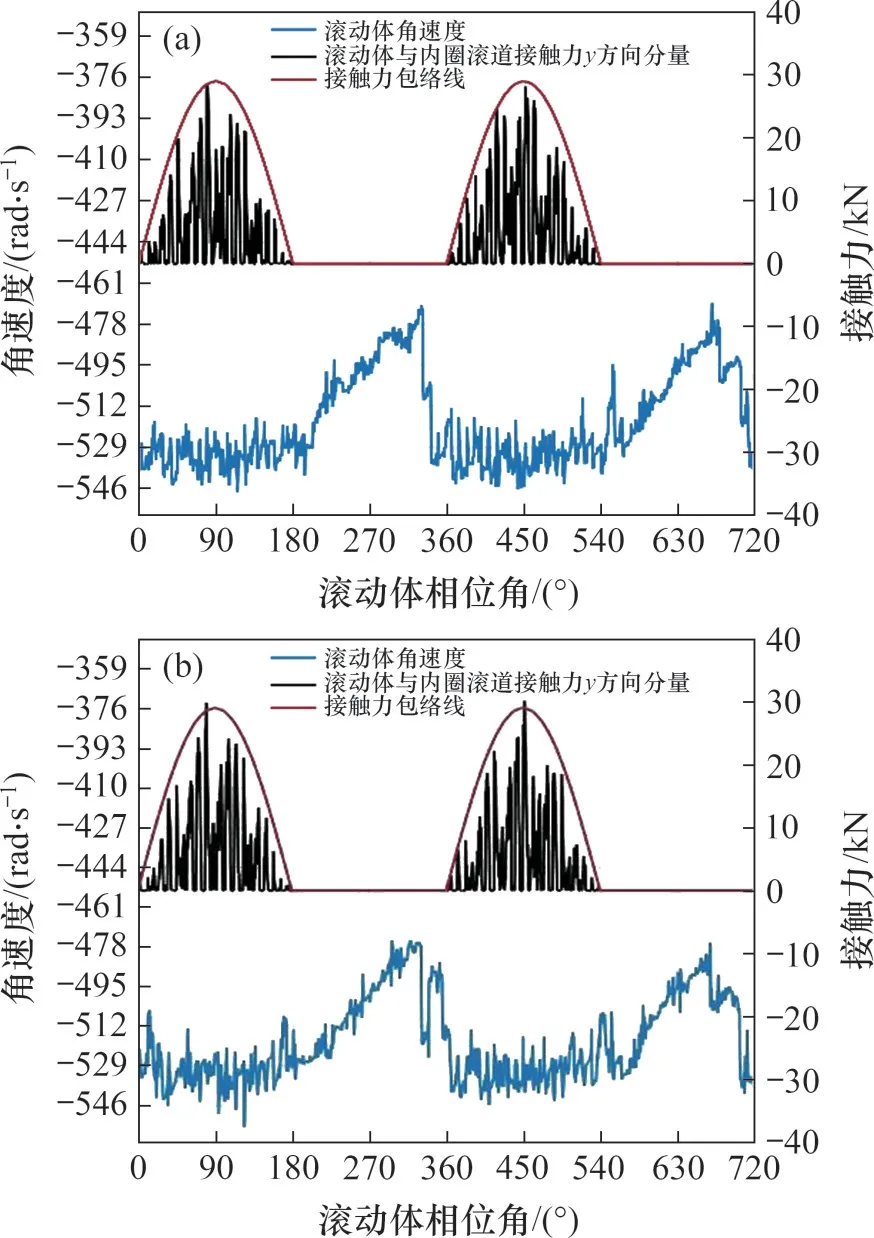
图6 无缺陷轴承两侧滚子动力学分析Fig.6 Dynamic analysis of rollers on both sides of defectfree bearing

外圈缺陷的轴承在高速列车运行工况下轴承左右两侧某滚子动力学分析结果见图7，其中，图7(a)所示为外圈无缺陷侧的某滚子动力学特性，图7(b)所示为外圈缺陷侧的某滚子动力学特性。由图7(a)可知：无缺陷侧的滚子动力学特性与无缺陷轴承左右两侧某滚子动力学特性基本一致。由图7(b)可知：滚子角速度在有缺陷的一侧区间A与区间D比无缺陷的一侧波动更大；当滚子运动到最大承载力处时，角速度出现1个激励波动，滚子与轴承内圈滚道接触力为0 N，这是滚子未与轴承内圈接触所致。

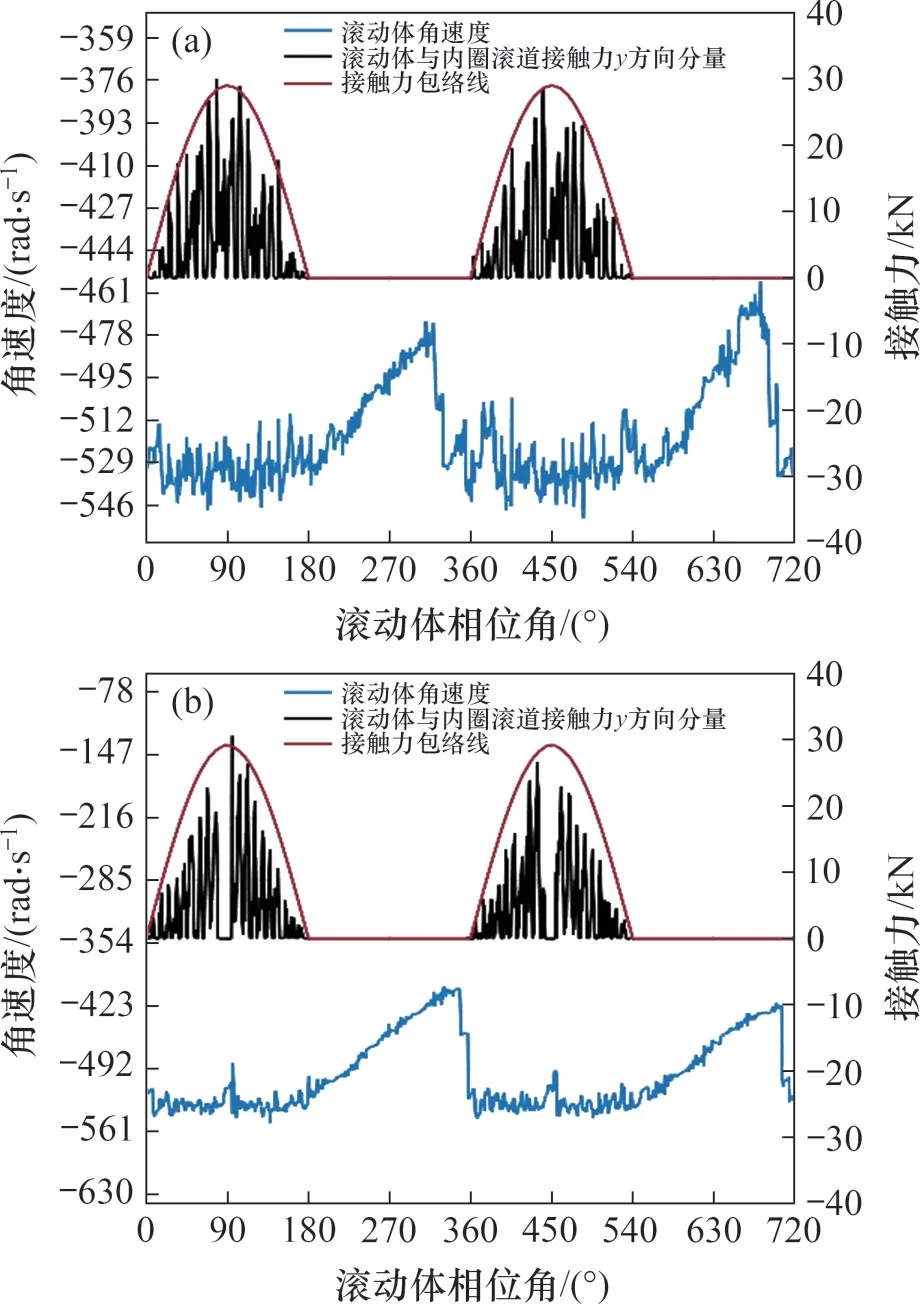
图7 外圈缺陷的轴承两侧滚子动力学分析Fig.7 Dynamic analysis of rollers on both sides of bearing with outer raceway defect

内圈缺陷的轴承在高速列车运行工况下轴承左右两侧某滚子动力学分析结果见图8，其中，图8(a)所示为内圈无缺陷侧的某滚子的动力学特性，图8(b)所示为内圈缺陷侧的某滚子的动力学特性。由图8(a)可知：无缺陷侧的滚子的动力学特性与前面所述无缺陷轴承左右两侧某滚子动力学特性基本一致。由图8(b)可知：有缺陷一侧的滚子角速度波动相对于无缺陷侧更大，在区间A1内角速度变化速度呈锯齿状增大，说明内圈缺陷导致滚子频繁打滑；在区间D，滚子由于脱离承载角速度在某点急剧减小。

图8 内圈缺陷的轴承两侧滚子动力学分析Fig.8 Dynamic analysis of rollers on both sides of bearing with inner raceway defect

滚子缺陷的轴承在高速列车运行工况下轴承左右两侧某滚子动力学分析结果见图9，其中，图9(a)所示为滚子缺陷侧具有缺陷的滚子动力学特性，图9(b)所示为滚子无缺陷侧某滚子的动力学特性。由图9(b)可知：无缺陷侧的滚子的动力学特性与前面所述无缺陷轴承左右两侧某滚子动力学特性基本一致。由图9(a)可知：当缺陷滚子在区间B与区间C时，滚子缺陷部分与滚道接触造成的摩擦力增大，但由于缺陷处摩擦力矩较正常滚子小，难以达到克服滚子几何缺陷需要的力矩，所以，滚子在区间B与区间C运动时角速度呈锯齿状频繁大幅度波动。

图9 滚子缺陷的轴承两侧滚子动力学分析Fig.9 Dynamic analysis of rollers on both sides of bearing with roller defect

保持架缺陷的轴承在高速列车运行工况下轴承左右两侧某滚子动力学分析结果见图10，其中，图10(a)所示为保持架缺陷侧某滚子的动力学特性，图10(b)所示为保持架无缺陷侧某滚子的动力学特性。由图10 可知：无论是否在缺陷侧，滚子的动力学特性与前面所述无缺陷轴承左右两侧某滚子动力学特性基本一致。这可能是因为保持架虽局部破损，但仍有大部分滚子托举保持架，未造成保持架运动过大的变化，在保持架兜孔破损位置的滚子虽然运动空间增大，但仍然具有承载能力，与无缺陷轴承中的滚子承载变化规律基本一致。

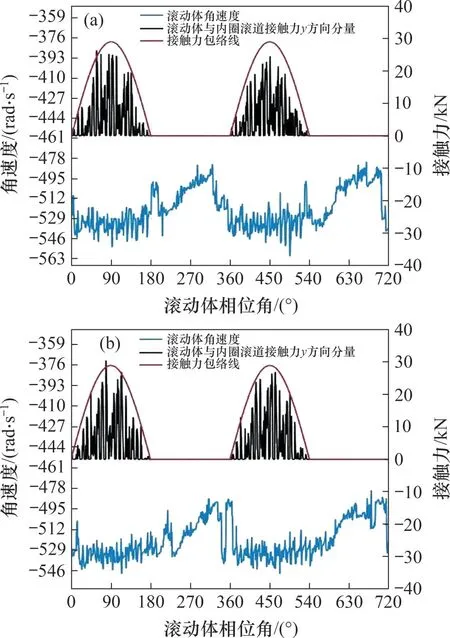
图 10 保持架缺陷的轴承两侧滚子动力学分析Fig.10 Dynamic analysis of rollers on both sides of bearing with cage defect

2.2 滚子打滑率对比分析

滚子与轴承内外圈滚道之间不仅存在相对滚动，而且存在相对滑动，滚子与轴承内外圈滚道之间存在的相对滑动运动可以用滚子的打滑率来描述。打滑率的定义如下：

式中：vt为滚子与滚道接触点处保持架纯滚动时的理论速度；vr为滚子与滚道接触点处滚子表面实际速度。

在高速列车运行工况下，无缺陷轴承及4种典型缺陷轴承的缺陷侧的滚子打滑率变化曲线分别如图11至图16所示。由图11可知：无缺陷轴承滚子打滑率随着滚子位置周期性变动，滚子打滑率从10%(承载区)到25%(非承载区)之间变化。由图12 可知：外圈缺陷轴承的缺陷侧滚子的打滑率从10%(承载区)到35%(非承载区)变化，并且在最大承载区位置，滚子打滑率有1个从10%到20%的波动激励，说明在该位置，滚子脱离了承载。由图13 可知：内圈缺陷轴承的缺陷侧滚子的打滑率从10%(承载区)到60%之间变化。由图14 和图15 可知：具有滚子缺陷的轴承，其缺陷滚子的打滑率在10%(承载区)到65%(非承载区)之间变化，但该缺陷对于同一侧的其他无缺陷的滚子打滑率基本没有影响。由图16 可知：保持架缺陷轴承的缺陷侧滚子的打滑率从10%(承载区)到20%(非承载区)之间变化。可见，无论是否具有缺陷，滚子的打滑率均在非承载区有所增大，外圈缺陷会导致滚子在非承载区的打滑率增大，内圈缺陷对滚子的打滑率影响最大，打滑率最大达到60%。

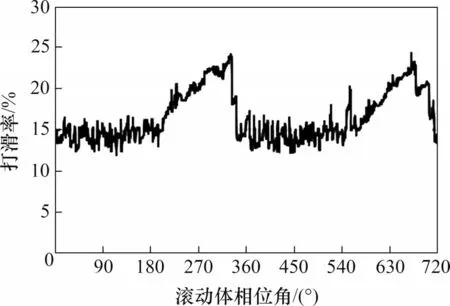
图11 无缺陷轴承滚子打滑率变化曲线Fig.11 Roller slip rate of bearing in defect-free case

图12 外圈缺陷轴承缺陷侧滚子打滑率变化曲线Fig.12 Roller slip rate on defect side of bearing with outer raceway defect

图13 内圈缺陷轴承缺陷侧滚子打滑率变化曲线Fig.13 Roller slip rate on defect side of bearing with inner raceway defect

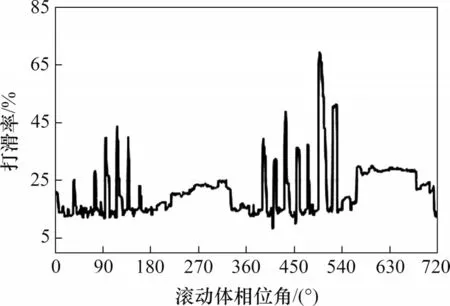
图14 滚子缺陷轴承缺陷滚子打滑率变化曲线Fig.14 Roller slip rate on defect side of bearing with roller defect

图15 滚子缺陷轴承缺陷侧非缺陷滚子打滑率变化曲线Fig.15 Defect-free roller slip rate on defect side of bearing with roller defect

图16 保持架缺陷轴承缺陷侧滚子打滑率变化曲线Fig.16 Roller slip rate on defect side of bearing with cage defect

2.3 保持架角速度对比分析

保持架角速度的稳定性可以评价轴承的动力学性能。在高速列车运行工况下，4种典型缺陷轴承的保持架角速度变化曲线分别如图17～图20所示。轴箱轴承在内圈转速为1 490 r/min工况下，保持架理论角速度为68.3 rad/s。由图17 可知：当保持架运动到稳定转速后，无故障侧保持架角速度比率(保持架实际角速度与理论角速度的比率)在97%～102%之间波动；外圈缺陷侧的保持架角速度比率在90%～102%之间波动，并且呈正弦半波周期性变化规律。由图18 可知：内圈缺陷侧的保持架角速度比率为100%～130%，呈非周期性高频激励波动的变化规律。由图19 可知：滚子缺陷侧保持架角速度比率为95%～105%，呈非周期性高频激励波动变化规律。由图20 可知：缺陷保持架的角速度比率为96%～102%，其角速度比率与无缺陷保持架的角速度比率基本一致。

图17 外圈缺陷轴承保持架角速度比率Fig.17 Cage angular velocity of bearing with outer raceway defect

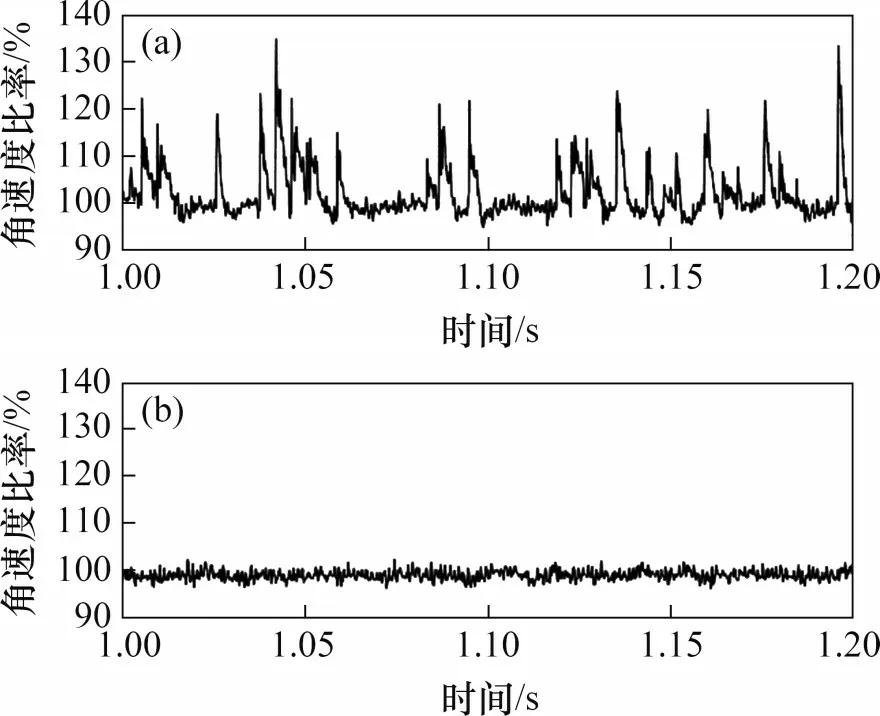
图18 内圈缺陷轴承保持架角速度比率Fig.18 Cage angular velocity of bearing with inner raceway defect

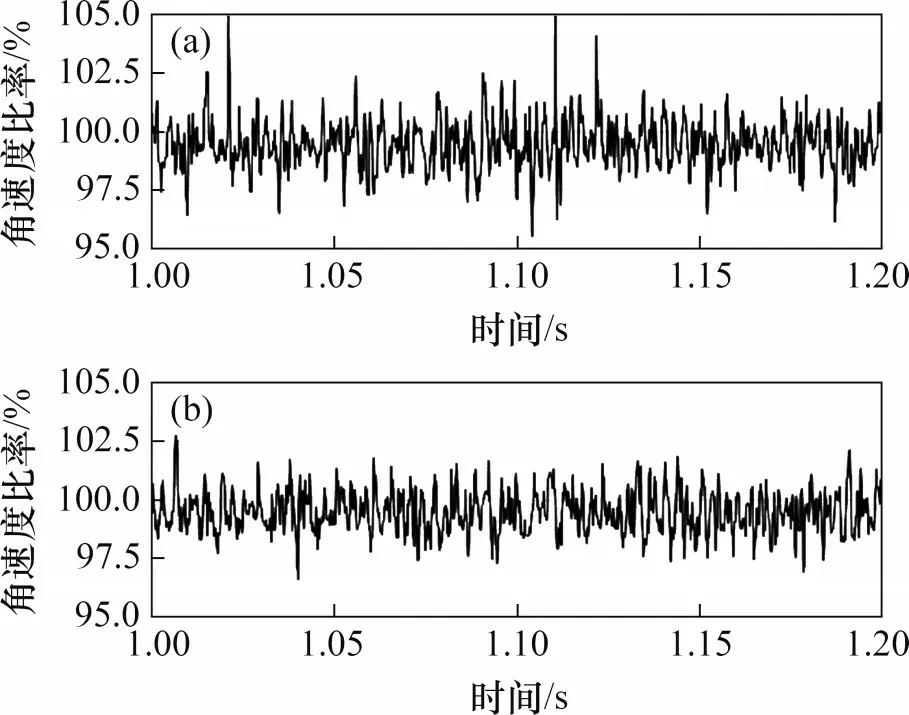
图19 滚子缺陷轴承保持架角速度比率Fig.19 Cage angular velocity of bearing with roller defect

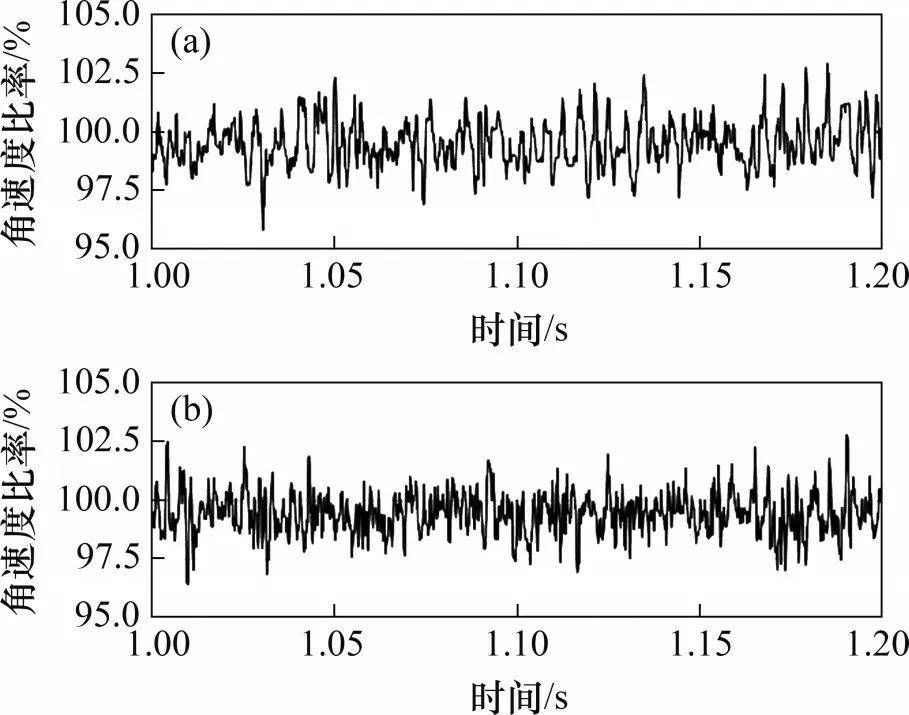
图20 保持架缺陷轴承保持架角速度比率Fig.20 Cage angular velocity of bearing with cage defect

3 高速列车轴箱轴承典型故障特征分析

3.1 4种典型缺陷的理论特征频率

轴承不同元件的频率对于监测轴承工作状态、分析轴承故障类型具有重要意义。保持架旋转频率fc为[17]

式中：ni为内圈转动频率；d为滚子直径；dp为轴承节圆直径；α为接触角。

内圈某一点相对保持架某一点的旋转频率为[17]

滚子通过外圈滚道上某一点的频率为[17]

式中：Z为轴承单侧滚子数量。滚子通过内圈滚道上某一点的频率为[17]

滚子绕自身轴的旋转频率为[17]

当高速列车运行速度为250 km/h 时，轴箱轴承的转速为1 490 r/min，此时，4 种典型缺陷理论特征频率可以通过式(4)～(8)计算，如表4所示。

表 4 1 490 r/min转速下轴箱轴承4种典型缺陷理论特征频率Table 4 Theoretical characteristic frequencies of four typical defects of axle box bearing at 1 490 r/min speed

3.2 4种典型缺陷的特征频率对比分析

Hilbert-Huang 变换(HHT)是经验模态分解(EMD)[18]和Hilbert 时频谱的统称。EMD-包络谱[19]即通过EMD方法获得目标信号不同IMF分量，再将IMF 分量进行Hilbert 解调后求幅值，最后，将幅值低通滤波后进行快速傅里叶变换(FFT)求出Hilbert包络谱，得到调制频率及高次谐波。

图21所示为在高速列车运行工况下轴箱轴承内圈加速度振动信号。在高速列车运行工况下，4种典型缺陷的轴箱轴承的EMD-包络谱图如图22～25所示。由图22 可知：IMF3 分量中明显有10.8 Hz频率信号，为保持架缺陷的1倍特征频率，在IMF1 分量与IMF2 分量图中有保持架缺陷高倍的特征频率，如325.4 Hz(30 倍特征频率)、336.2 Hz(31倍特征频率)、347 Hz(32倍特征频率)、357.8 Hz(33倍特征频率)、390.4 Hz(36倍特征频率)等，其相对误差分别为0.49%，0.56%，0.52%，0.53%与0.51%。保持架由于打滑等因素，其实际角速度与理论角速度有一定差异，将保持架实际角速度换算成转动频率为10.839 Hz，经过换算后，保持架缺陷特征频率分别为10.8 Hz(1 倍特征频率)、325.2 Hz(30倍特征频率)、336.0 Hz(31倍特征频率)、346.9 Hz(32倍特征频率)、357.7 Hz(33倍特征频率)、390.2 Hz(36 倍特征频率)，以上多个单(多)倍实际特征频率与换算后理论特征频率的相对误差分别为0，0.06%，0.06%，0.03%，0.03%和0.05%。由图23 可知：IMF1 分量、IMF2 分量与IMF3 分量包络图中明显有195.4 Hz 频率信号，为外圈缺陷的1 倍特征频率，其相对误差为0.15%。由式(6)可知，外圈缺陷特征频率与保持架转动频率也相关，将换算后的保持架转动频率代入式(6)得到外圈缺陷特征频率为195.1 Hz，实际特征频率与换算后理论特征频率的相对误差为0.15%。由图24 可知：IMF1 分量、IMF2 分量与IMF3 分量包络图中有242.8 Hz信号，其为内圈缺陷的1倍特征频率，相对误差为3.4%。由式(7)可知，内圈缺陷特征频率与保持架转动频率有关，将内圈缺陷工况下的保持架平均角速度转动频率13.47 Hz 代入式(7)，获得内圈缺陷换算后特征频率为242.5 Hz，与图26 中内圈缺陷特征频率242.8 Hz 相近，相对误差为0.12%。由此可知，当不考虑摩擦打滑与保持架效应因素时，理论特征频率公式计算的特征频率误差较大。由图25 可知：IMF1 分量与IMF2分量包络图中有390.4 Hz信号，其为滚子缺陷4倍特征频率，相对误差为0.93%。由于滚子打滑率波动较大，使用平均角速度对理论特征频率进行换算并不理想。实际特征频率与换算后特征频率对比如表5与表6所示。

表 6 4种典型缺陷特征频率相对误差对比Table 6 Comparison in relative errors of characteristic frequencies of four typical types of defects

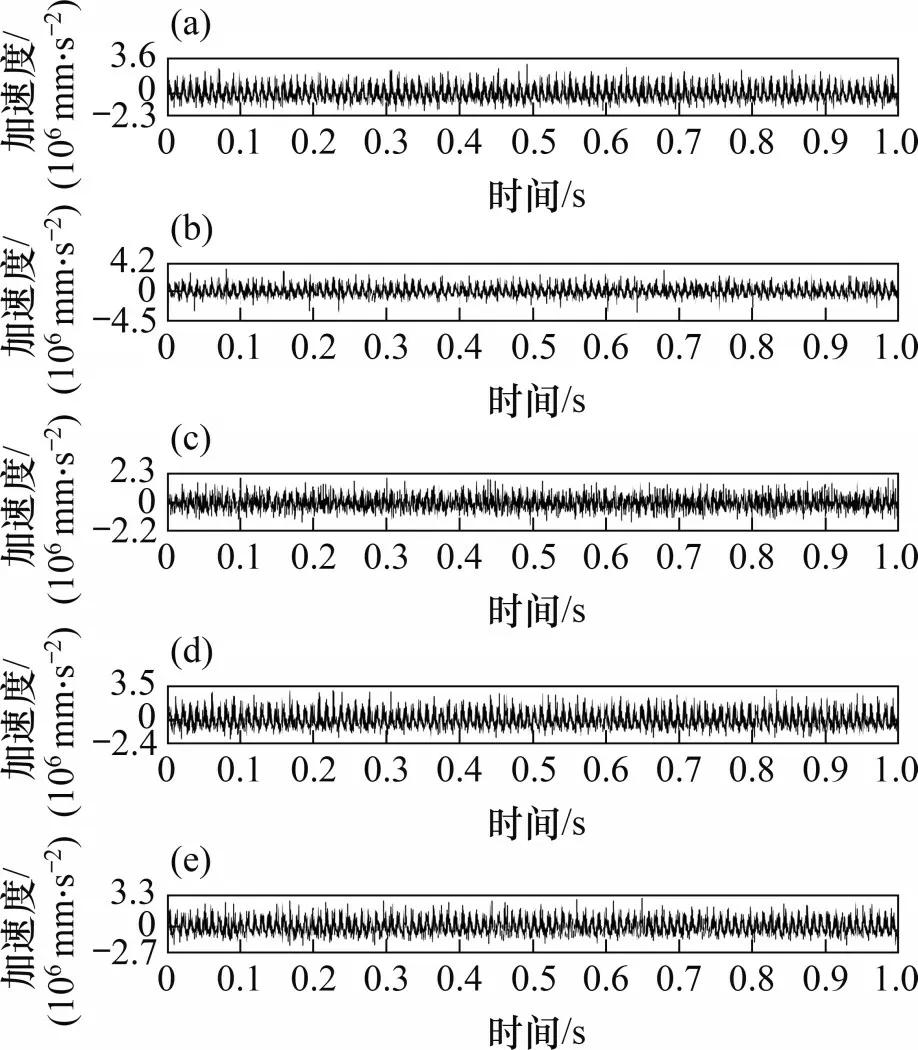
图21 高速列车轴箱轴承加速度振动信号Fig.21 Acceleration vibration signal of axle box bearing of high speed train

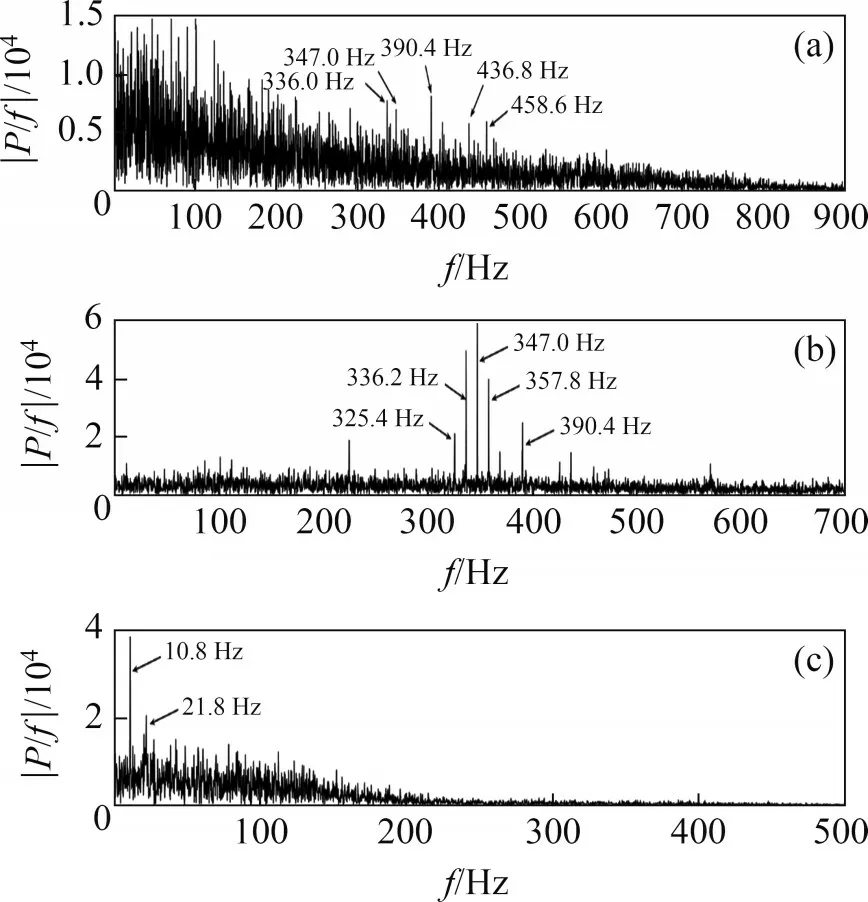
图22 保持架缺陷轴承EMD-包络谱Fig.22 EMD-envelope spectrum of bearings with cage defect

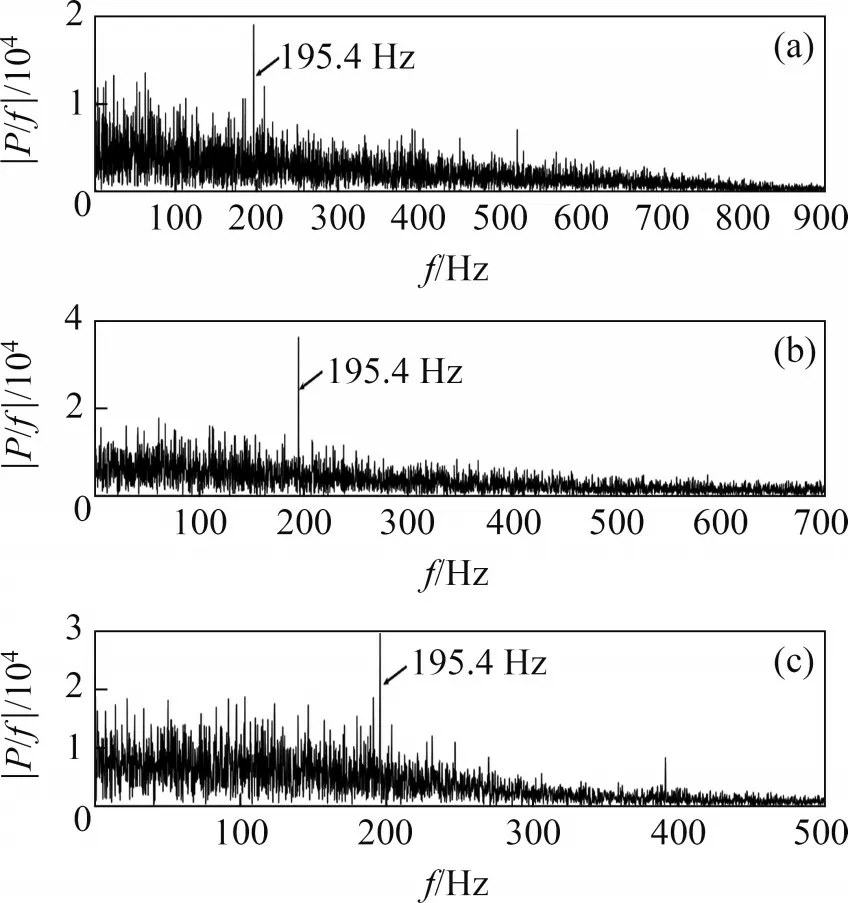
图23 外圈缺陷轴承EMD-包络谱Fig.23 EMD-envelope spectrum of bearings with outer raceway defects

图24 内圈缺陷轴承EMD-包络谱Fig.24 EMD-envelope spectrum of bearings with inner raceway defects

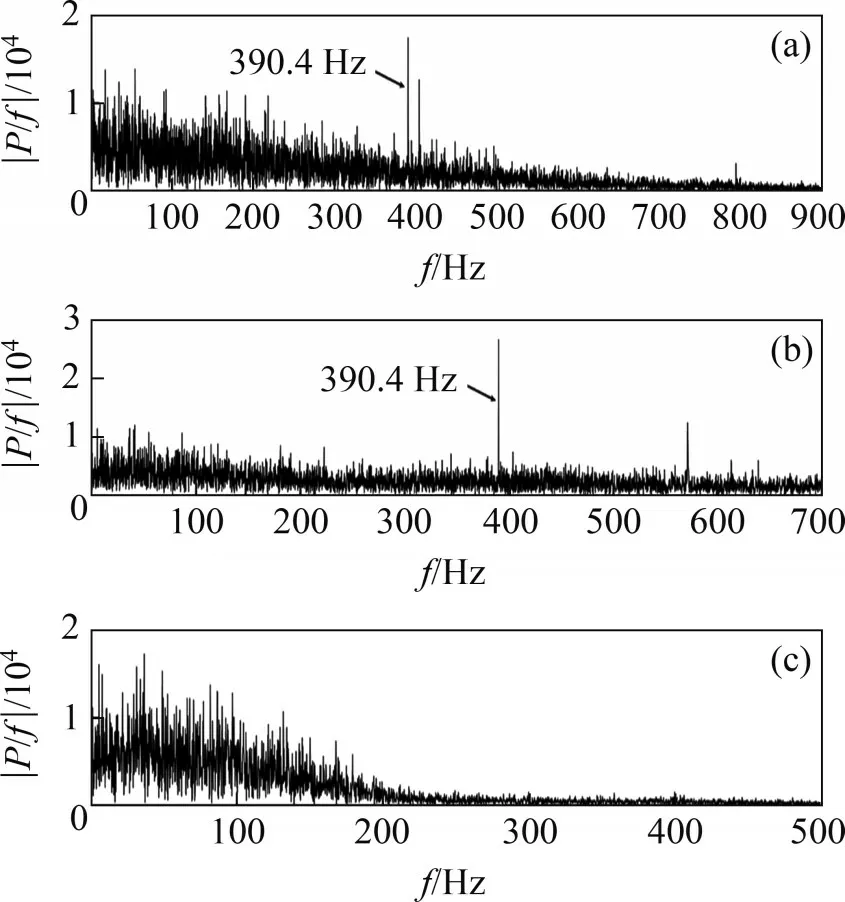
图25 滚子缺陷轴承EMD-包络谱Fig.25 EMD-envelope spectrum of bearings with roller defects

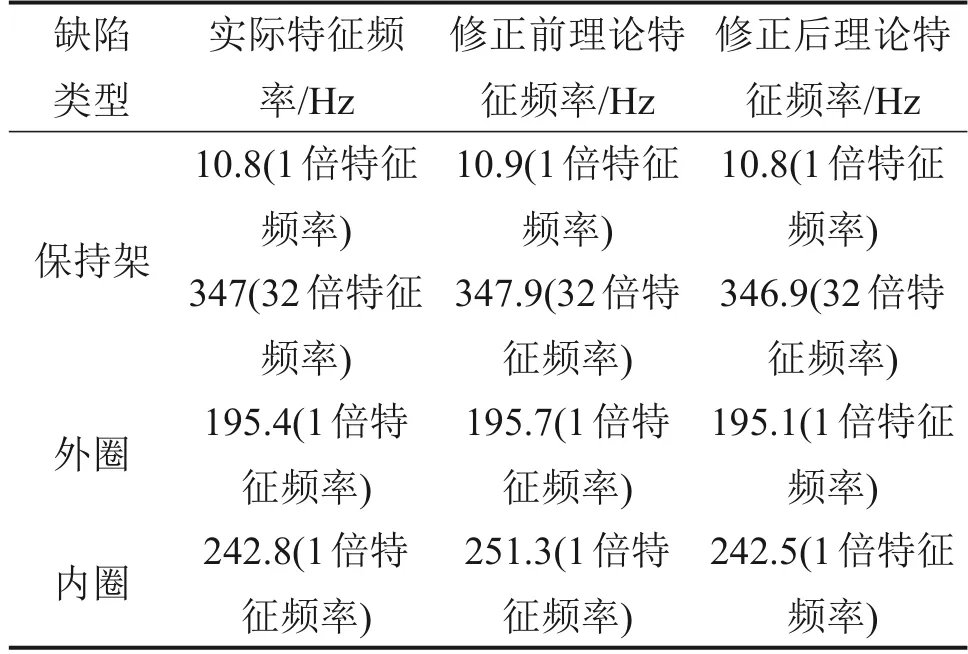
表5 4种典型缺陷特征频率对比Table 5 Comparison in characteristic frequencies of four typical types of defects

造成特征频率误差的原因可能有：1)模型考虑了保持架的打滑效应与保持架运动的不稳定性，保持架的打滑效应在一定程度上改变了保持架的理论特征频率，保持架运动的不稳定性会改变保持架的瞬时理论特征频率；2)滚子在不同运动区间的打滑效应也将在一定程度上影响滚子缺陷与内圈缺陷的特征频率，同时，由于滚子的打滑率波动较大，使得滚子缺陷理论特征频率不能使用滚子平均角速度进行修正。从表5可见：修正后理论特征频率与实际特征频率的相对误差减小，相对误差均在0.15%以内，其中，内圈缺陷特征频率相对误差由3.50%下降到0.12%。综上可知，理论特征频率计算公式需要充分考虑滚子-滚道摩擦打滑与滚子-保持架兜孔碰撞效应的影响。

4 结论

1)考虑滚动轴承元件摩擦打滑、保持架效应等因素，采用MSC Adams 建立了高速列车轴箱轴承完全动力学模型，并验证了该模型的有效性。

2)无论轴承是否具有缺陷，滚子的打滑率均在非承载区有所增大；外圈缺陷轴承的滚子角速度比正常运行轴承的滚子角速度稍小；内圈缺陷对滚子动力学特性影响较大，滚子角速度波动较大；而滚子缺陷仅对缺陷的滚子的动力学特性影响较大，滚子角速度波动较大；保持架缺陷对滚子动力学特性的影响较小，滚子角速度与正常运行的角速度基本无差异。

3)外圈缺陷会导致保持架角速度偏低于理论角速度，保持架角速度比率呈正弦半波周期性变化；内圈缺陷会导致保持架角速度偏高于理论角速度，保持架角速度比率呈非周期性激励波动变化，且波动频率较高；滚子与保持架缺陷对保持架动力学特性的影响很小，其保持架角速度与正常运行的保持架基本无差异。

4)理论特征频率计算公式需要充分考虑滚子-滚道摩擦打滑与滚子-保持架兜孔碰撞效应的影响。