基于改进条件概率的贝叶斯网络隧道坍塌安全风险评价

陈钊，袁航，黄鹏宇，周子龙，王秉

(1.广西北投公路建设投资集团有限公司，广西 南宁，530028；2.中南大学 土木工程学院，湖南 长沙，410083；3.中南大学 资源与安全工程学院，湖南 长沙，410083)

近年来，我国隧道建设规模逐渐扩大，截至2019年，我国公路隧道数量为19 067 座，同比增长7.5%；隧道总长度达到1 896.66万m，同比增长10%。随着隧道建设规模的日益扩大，隧道施工事故也频频发生。在收集相关资料和整理文献[1-3]的数据后，对2005—2019年间我国隧道施工发生的136起事故进行分析后发现，坍塌事故发生次数占总事故次数的70.85%；坍塌事故造成的死亡人数占总人数的48.35%。由此可见，在隧道施工过程中，坍塌事故最经常发生，造成的后果最为严重。对建设中的隧道进行坍塌安全风险评估和风险发生概率等级评估，对现场事故的预防及安全管控具有重大意义。

目前，国内外学者对隧道坍塌风险评价进行了一些创新性研究。亓晓贵等[4-5]利用模糊综合评价法对隧道坍塌进行了风险评价；王天瑜等[6]运用未知测度理论建立了隧道坍塌风险预警系统；杨光等[7]运用云模型理论确定不同风险等级的确定度，由最大确定度判断隧道塌方等级。但上述方法多是定性或半定量评价，存在很强的不确定性，并且无法进行定量风险概率计算及事故原因诊断。而贝叶斯网络具有很强的概率推算、处理复杂不确定性信息问题以及进行故障诊断的能力，是一种应用广泛的风险概率定量分析方法，目前已经在隧道风险评价中应用广泛。孙景来[8]将隧道坍塌事故树转化为贝叶斯网络结构，利用专家调查和案例事故的数据得出节点条件概率用于隧道坍塌评价；FENG 等[9]建立了朴素贝叶斯分类器，编制了隧道病害数据库用于分类器学习，将训练好的分类器用于隧道坍塌评价；姜洲等[10]结合专家及历史数据获得条件概率，利用贝叶斯正向和反向推理计算运营隧道渗漏水风险概率并进行原因诊断；吕杉[11]利用noisy-gate 模型获得各节点的条件概率，构建贝叶斯网络二态模型进行地铁隧道施工风险控制；李泽荃等[12]利用以往事故案例中各事件的依赖关系得到条件概率结构，结合区间概率等级划分与权重信心指标法计算事件概率。SUN 等[13-14]建立了多态模糊贝叶斯网络隧道坍塌模型，以模糊函数对多状态节点进行描述，根据专家调查权重对条件概率进行赋值；JING 等[15]基于历史事故统计和专家经验等数据开发了隧道坍塌贝叶斯网络风险预测软件，并应用到实际的隧道当中；陈发达等[16]利用云模型归属各节点的状态，构建了基于云贝叶斯网络的泥水盾构隧道开挖面稳定性研究模型；吴贤国等[17]将可对不确定信息进行有效融合的证据理论引入贝叶斯网络先验概率的确定过程中，对条件概率进行赋值设计，开展了盾构下穿既有隧道的安全风险评估。然而，上述研究对于贝叶斯条件概率结构的确定大多采用历史数据和专家逐一决策、平均集成相结合或专家依据自身经验进行主观赋值设计的方法，这些方法忽略了专家在专业领域、知识背景、认知程度等诸多方面的差异，这种差异会造成过度决策或决策不足，并且平均集成各专家数据缺乏科学依据[18-19]；同时，专家决策过多不仅实用性低，而且会造成条件概率确定过程计算效率低、主观性较强，导致最终风险概率误差较大，难以较好地实现隧道坍塌风险控制与预警。

考虑目前贝叶斯网络隧道坍塌风险评价中存在的专家决策次数多、主观性大、条件概率计算效率低、误差大等不足，本文将权重与DS证据理论引入贝叶斯网络条件概率的确定过程。利用DS证据理论有效融合部分特殊状态条件概率的不同专家决策信息源；结合各节点事件的权重和特殊节点状态下的条件概率定义“状态危险贡献值”用于求解所有的条件概率，对条件概率确定过程进行改进，以期更好地实现隧道坍塌风险评价。

1 基本方法与风险评价模型构建

1.1 改进条件概率的贝叶斯网络

一个完整的贝叶斯网络由根节点X、中间节点M、叶节点T、根节点先验概率P(X)以及条件概率[P(M|X)，P(T|M)]这几部分组成。如图1 左上角为一个简单的贝叶斯网络，节点间有条件关系的互为父子节点；如X为M的父节点，T为M的子节点，各节点通过条件概率联系在一起，条件概率反映了父子节点间的连接强度关系。贝叶斯网络的本质是概率的推理计算，节点T的发生概率可通过下式求得：

为了与实际情况对应，需将贝叶斯网络各节点进行安全状态划分，不同的安全状态对应实际中各事件的不同风险等级。对于某个子节点，其父节点的所有安全状态组合数对应该父子节点间的条件概率组数。在条件概率的确定过程中，传统方法全部的条件概率都是依靠专家决策确定的，对于结构简单，节点状态分类少的贝叶斯网络，专家决策次数较少，但是对于隧道坍塌这种多因素导致的事故，其贝叶斯网络结构复杂，根节点安全状态分类较多，按照传统的方法，对所有安全状态组合进行一一枚举，专家进行逐一决策，其条件概率超过万组，需要专家决策超过万次，这在实际中很难办到，并且节点状态微小变动而导致的条件概率变化幅度较小，这在专家决策中很难准确地体现，因此，需要对条件概率确定过程进行改进。图1所示为子节点M1与其父节点X1，X2和X3之间传统方法与改进方法条件概率确定过程。假设子节点M1包含0和1这2种安全状态，父节点X1，X2和X3均包含0，1 和2 这3 种安全状态，共有27 组条件概率，每组包含2 个概率。图1 中，表示不同安全状态下的节点Xi(i=1，2，3)，M b1(b=0，1)表示不同安全状态下的节点M1，b表示节点M1的安全状态取值；表示条件概率，其中，q=1，2，…，27表示条件概率的组数，b=0或1 分别表示M1处于状态0 或1；wi(i=1，2，3)表示节点Xi权重；Δj(j=1，2)表示节点整体的状态危险贡献值。

从图1可以看出：选择同一安全状态组合的特殊条件概率进行专家决策，这种状态组合的信息复杂度最小，最容易进行决策，因而可以提高专家决策的可信度，然后根据同一状态组合的条件概率，结合节点的权重，定义状态危险贡献值，可以求出所有状态组合的条件概率，采用这种方法时，专家决策的次数等于根节点安全状态的最大值，从而减少专家决策次数，降低了主观性，减小了误差。

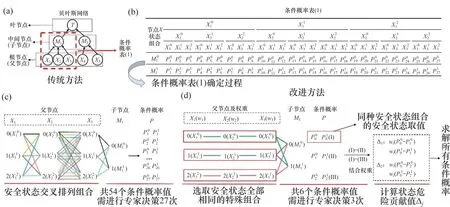
图1 改进条件概率的贝叶斯网络内涵图Fig.1 Bayesian networks intension graph with improved conditional probability

1.2 基于改进条件概率的贝叶斯网络风险评价模型

基于改进条件概率的贝叶斯网络风险概率求解的技术路线如图2所示，主要包括3 个阶段：1)确定风险评价指标体系及各指标的风险等级分类标准；2)构建贝叶斯网络结构，并确定根节点先验概率及改进的条件概率这2部分贝叶斯网络参数；3)进行风险概率推理及分析，计算叶节点的概率并由叶节点的概率反向推算根节点的后验概率。

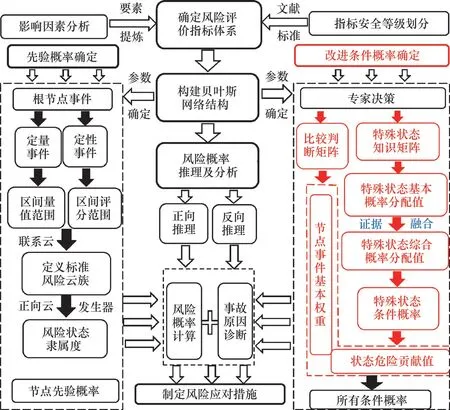
图2 改进条件概率的贝叶斯网络风险概率计算技术路线图Fig.2 A technical roadmap for risk probability calculation in Bayesian networks with improved conditional probability

1.2.1 风险评价指标体系确定

通过参考文献[20-22]、分析历史坍塌事故数据以及专家经验，确定导致隧道坍塌的二级风险事件主要包括5 个方面，分别涉及隧道的水文条件、安全管理能力、围岩稳定性、地质条件、设计方案合理性。基本风险事件划分如下：水文条件包括区域年均降雨量、地下水状态、渗水状态、周围水体情况；安全管理能力包括作业人员经验、安全管理人员配备情况、安全投入、历史事故情况；围岩稳定性包括围岩强度、岩层倾角、岩体完整性系数；地质条件包括岩溶发育情况、地质符合性、岩爆水平、偏压、断层破碎带和隧道埋深；设计方案合理性包括洞口形式、隧道全长、开挖断面形式、施工步距、循环进尺。

将指标的风险等级状态与事件在贝叶斯网络中安全状态对应起来，可分为3状态事件和4状态事件。对于3 状态事件，用0，1 和2 分别代表安全、一般、危险这3种风险等级状态；对于4状态事件，用0，1，2和3分别代表安全、一般、较危险、危险这4种风险等级状态。将基本风险事件分为定性事件和定量事件2大类。对于定量事件，其安全状态依据是定量的数值区间，参考文献[6-7，17，21-23]中的分类标准对其进行安全状态划分。表1所示为定量事件安全状态划分标准，其中，施工步距的划分标准考虑的是围岩衬砌到掌子面距离。

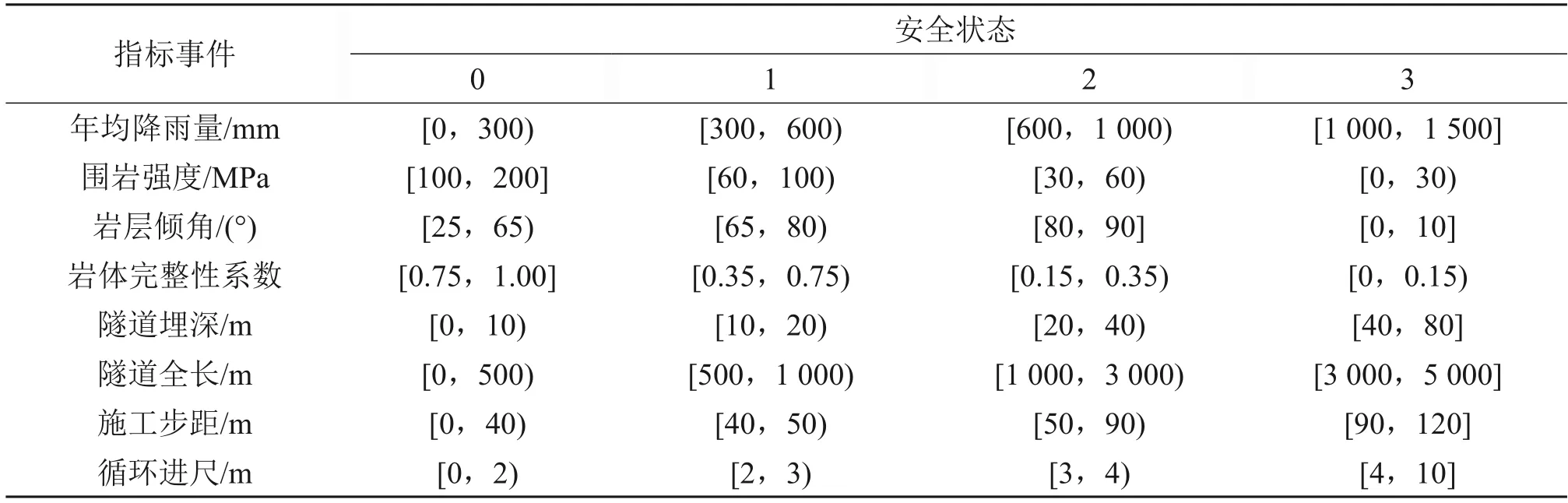
表1 定量事件安全状态划分标准Table 1 Criteria for security-state division of quantitative events

对于定性事件，其分类标准是定性的语言描述，参考文献[23]采用10分制进行评判，对于4状态事件，其划分结果为安全[7.5～10]、一般[5～7.5)、较危险[2.5～5)、危险[0～2.5)；对于3状态节点，其划分结果为安全[7～10]、一般[3～7)、危险[0～3)；定性事件由专家根据实际条件对照定性描述标准进行打分。表2所示为定性事件安全状态划分标准，其中开挖断面和洞口形式这2类指标事件分类标准的描述是确定性的，其所属安全状态是唯一确定的，其概率为1，并且依据实际情况可以准确地判断其所处的安全状态，因此无须进行打分评判。

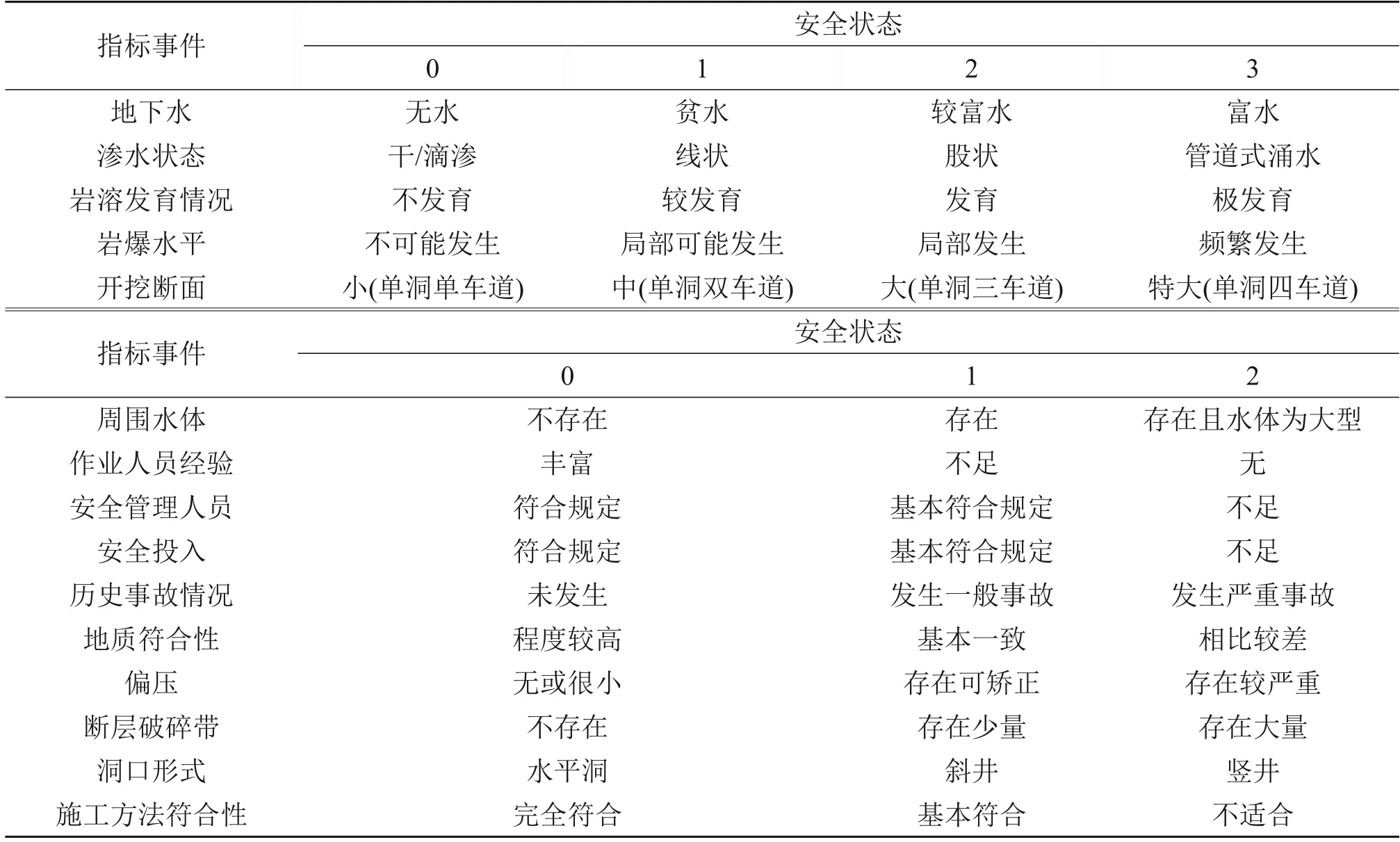
表2 定性事件安全状态划分标准Table 2 Criteria for security-state division of qualitative events

1.2.2 网络结构构建

贝叶斯网络风险评价模型由网络结构和网络参数2部分组成，因此，需要进行结构设计和概率参数确定。首先，根据评价指标和风险等级划分，确定贝叶斯网络节点和节点状态，将基本风险事件作为根节点，二级风险事件作为中间节点，隧道坍塌作为叶节点，根节点安全状态划分如1.2.1节，中间节点以及叶节点的安全状态均以4状态来考虑。参数确定分为2部分，先验概率通过联系云确定；改进的条件概率依据专家决策信息，通过DS 证据理论和基本权重值共同确定，具体过程如下文所述。

1)根节点先验概率确定。

云模型能够反映样本实际指标分布情况，并能实现评价指标与评价等级间的确定和不确定关系统一定量描述。联系云是云模型的拓展，能够解决区间分布的评价指标在实际中应用的局限性。联系云由以期望值Ex为分界点的左、右2个不同特征的云滴构成。利用联系云构建根节点各安全状态的标准风险云族，标准云数字特征(Ex，En，He，a，k)计算公式为[24]

式中：i=0或1分别表示左半支和右半支云滴情况；Ex，En和He分别为左半支或右半支联系云的期望值、熵和超熵；Lmax和Lmin分别为区间的上、下限；ki为a'i相对应的分布密度函数的阶数；a'i为联系云修正后的半区间长度；为以En为期望；为方差生成的正态随机数；ai为联系云半区间长度。

若评价指标分类标准区间值随着风险增大而增加，该区间的左、右半区间长度为

若评价指标分类标准区间值随着风险增大而减少，该区间的左、右半区间长度为

云滴基于数字特征(Ex，En，H，a，k)和云滴数N产生，云滴x隶属度μ(x)计算公式为[24]

式中：a'为联系云修正后的半区长度。

利用正向云发生器计算根节点属于各安全状态的隶属度。首先输入节点各安全状态的标准云数字特征(Ex，En，He，a，k)及节点的实际取值x，然后生成以En为期望，He为标准差的正态随机数E′n，最后依据式(5)计算得到节点实际值属于各安全状态的隶属度，通过多次生成随机数，避免随机性带来的不确定性误差，最后求出平均隶属度。各安全状态之间相互独立，因此根节点属于各安全状态之间的隶属度之间相互独立，且属于各状态的隶属度和不为1，而在概率论中，一个事件属于其所有可能发生状态的先验概率和应为1，因此，利用隶属度—概率[16]转换公式将隶属度转换为相应的概率作为贝叶斯网络的先验概率：

式中：μ(x)i(i=1，2，…，n)为节点属于不同安全状态的隶属度；P[μ(x)i]表示节点属于不同安全状态的先验概率。

2)改进条件概率确定。

条件概率考虑的是子节点在其所有父节点处于不同状态组合下发生的可能性。考虑子节点对某一个父节点的影响程度，即可得到父子节点事件之间的权重关系，以往的条件概率计算过程中未考虑节点权重的作用。利用两两比较法构建判断矩阵用于计算权重向量w，具体计算方法同文献[25]。

DS 证据理论是由Dempster 提出，后经过Shafer 改进，故称为DS 证据理论。证据理论是概率理论的一种推广，是一种处理融合不确定信息问题的理想工具。其主要定义如下：

定义1：识别框架。设某一节点X，对于该节点所有可能发生的状态用一个集合θ(X)来表示，θ(X)中的各元素代表的状态是两两互斥的，称这样的集合θ(X)为节点X的识别框架。

定义2：基本概率分配函数m。概率函数m∈[0，1]，若满足条件：

其中：A为θ(X)的任一子集，则称m(A)为θ(X)上的基本概率分配函数。

定义3：合成规则。设m1(A)，m2(B)为θ(X)上的两个相互独立的不同信息源得到的基本概率分配值，集合A和B中元素分别为Ai和Bj，为了同时利用来自相互独立的不同信息源，DS 证据理论按照下式[18]求得2组数据融合后的概率分配值m(Ck)：

定义4：信度函数与似然函数。在识别框架θ(X)下，依据融合后的概率分配值m(Ck)，框架θ(X)中任一元素x的条件概率可通过下式量纲一化处理求出[18]：

式中：Ck(k=1，2，…)为集合C中的元素；Bel(x)为似然函数，表示融合后信息对x为真的最低信任程度；Pl(x)为信度函数，表示融合后信息对x为真的最高信任程度；π为信度函数与似然函数的折合因子。

对于贝叶斯网络中的任意一组子节点M与其父节点X1，X2，…，Xn，若子节点安全状态取值表示为b(b=0，1，2，…，k)，每个父节点安全状态取值表示为ai(i=1，2，…，n；ai=0，1，2，…，m)，则父节点一共有(m+1)n种安全状态组合，对应有(m+1)n组条件概率，每组条件概率中包含子节点的(k+1)种安全状态情况，则条件概率共有(k+1)(m+1)n个。选取父节点X均处于同一安全状态的特殊状态组合进行专家决策，建立如表3所示的专家决策知识矩阵，一共需进行(m+1)次专家决策。

表3 专家决策知识矩阵Table 3 Expert decision knowledge matrix

表3 中，Pai(Mb)(ai=0，1，2，…，m；b=0，1，2，…，k)表示父节点全部处于ai安全状态这种组合时，子节点M分别属于k+1种安全状态b的条件概率，其满足；θ(M)为定义1的属于子节点M条件概率的识别框架，即为集合…，m)。知识矩阵中的“1”表示元素与自身比较，“0”表示2 元素之间未进行比较，2，…，k)表示专家e对该元素与识别框架θ(M)进行相对发生可能性推断的决策值，该元素相对于识别框架发生可能性越高，表明该元素在识别框架中所占比例越高，所代表的基本概率就越大。采用2-6标度法进行赋值[19]，极端可能发生和一般可能发生分别赋值为6 和2，否则根据相对发生可能性给出介于6和2之间的整数。

按照下面公式求出专家e决策知识矩阵的最大特征值对应的归一化特征向量作为识别框架θ(M)的基本概率分配函数m(xi)(i=1，2，…，k+2)。

式中：m(xi)(i=1，2，…，k+1)表示集合θ(M)中第i个元素xi的基本概率分配值；m(xi)(i=k+2)表示识别框架θ(M)的基本概率分配值。

将所有专家各自决策的识别框架θ(M)基本概率分配函数按照式(7)进行逐一融合，得到识别框架θ(M)综合基本概率分配值mˉ，通过式(8)可以求出识别框架中各单个元素的条件概率。按照上述步骤可求出父节点全部处于同一安全状态组合时子节点属于各安全状态的条件概率，这些特殊状态组合信息复杂度最少、决策过程最简单、主观性最低、可信度最高。由上述方法求得的m+1 种特殊状态条件概率集合依次序表示如下：{P0(M0)，P0(M1)，P0(M2)，…，P0(Mk)}，{P1(M0)，P1(M1)，P1(M2)，…，P1(Mk)}，{P2(M0)，P2(M1)，P2(M2)，…，P2(Mk)}，……，{Pm(M0)，Pm(M1)，Pm(M2)，…，Pm(Mk)}。对于其余的[(m+1)n-m-1]种状态组合的条件概率，若继续采用专家决策，不仅增加专家决策量，同时效率低下；而且由于各节点安全状态的共同变化导致信息复杂度增加，决策难度增加，导致这些变化很难通过专家决策准确地体现出来。故其余的条件概率求解过程不依靠专家决策，采用一种结合节点权重与安全状态之间联系的方法求解。

令第1个集合中的各元素分别与剩下m个集合中对应元素相减，定义状态危险贡献值集合Δr(r=1，2，…，m)为

Δr(r=0，1，2，…，m)为“r”状态危险贡献值，表示由于父节点安全状态恶化对条件概率变化的贡献值。Δr(r=0，1，2，…，m)为所有父节点整体的变化量，而权重反映了单个父节点对子节点的影响程度，因此，结合各节点权重将整体状态危险贡献值按下式分配给每个节点：

式中：a1，a2，…，an表示节点X1，X2，…，Xn的安全状态取值。

1.2.3 风险概率推理及分析

按照1.1节中所述的贝叶斯网络基本原理，对应的贝叶斯网络正向推理叶节点Tq(q=0，1，2，…)的概率P(Tq)可通下式求得：

式中：Π为父节点集合表示方式，0，1，2，…，αi)分别表示不同状态下的中间节点和根节点，其中bj和ai分别表示节点M和X的安全状态取值，…，αi)为根节点Xi处于ai安全状态时的先验概率。

在已知叶节点T的安全状态Tq的概率时，结合贝叶斯网络反向推理可求得根节点安全状态为时的后验概率后验概率反映了根节点对叶节点的重要度，因此可以进行故障原因诊断，后验概率最大的根节点是导致叶节点发生的最主要原因。后验概率可通过下式[26]求得：

2 实例分析

2.1 工程概况

本文依托广西壮族自治区来宾市G355 蒙山至金秀公路老山隧道工程。拟建老山隧道工程概况见表4。隧道施工段，围岩主要由残坡积粉质黏土和强中风化砂岩、砂岩夹泥质、砂岩夹页岩组成，属岩土组合围岩。粉质黏土层较薄，呈硬塑状，结构较松散。下伏强中风化砂岩、砂岩夹泥质、砂岩夹页岩，局部裂隙发育，岩体破碎，稳定性较差。围岩岩体较破碎，节理裂隙发育，呈碎裂状结构，围岩有不稳定因素，易发生冒顶片帮事故，隧道开挖后洞室以淋雨状出水为主，强降雨后局部可能会出现小股状涌水现象，导致在隧道开挖过程中，可能会发生严重塌方、冒顶事故，因此需提前进行风险评估。

表4 隧道工程概况一览表Table 4 Overview list of tunnel works

2.2 隧道坍塌贝叶斯网络结构构建

根据1.2.1 节中所建立的风险指标体系，结合工程实际、现场专家经验以及施工单位历史数据，建立的隧道坍塌贝叶斯网络结构图如图3所示。

2.3 隧道坍塌贝叶斯参数确定

2.3.1 先验概率确定

结合老山隧道的地质水文条件以及施工现场资料，得到隧道坍塌的基本事件中的定量型事件的基本参数，同时，结合表2的定性描述分类标准对隧道现场的定性事件进行赋分。隧道开挖断面形式(X18)采用单洞双车道，属于安全状态2，洞口形式(X20)为竖井，属于安全状态1，这2 个节点事件无须进行赋分计算，各根节点事件的取值或得分见表5。

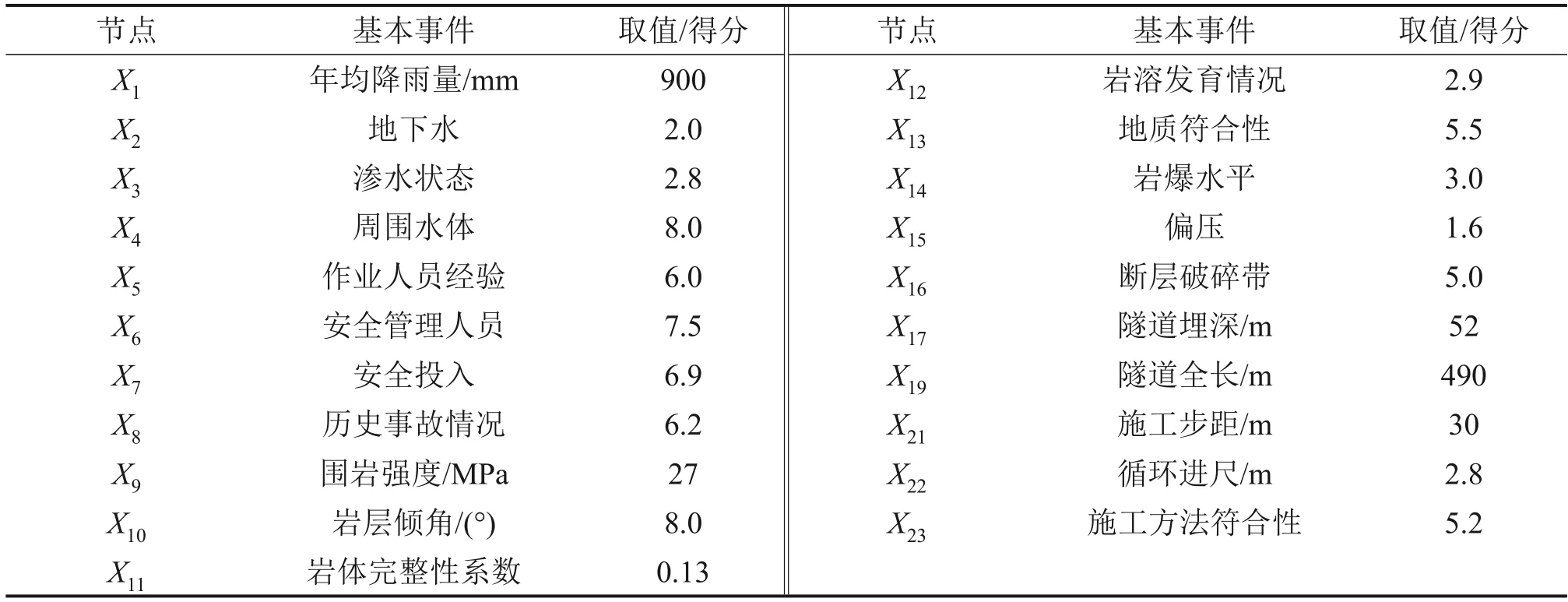
表5 根节点事件取值及得分Table 5 Event value and score of root node

依据表1和表2中的安全状态划分标准，利用式(2)～(4)求出根节点事件的各安全状态标准联系云特征值，依据式(5)和式(6)计算基本事件属于各安全状态的隶属度以及对应于各安全状态的先验概率，结果如表6所示。

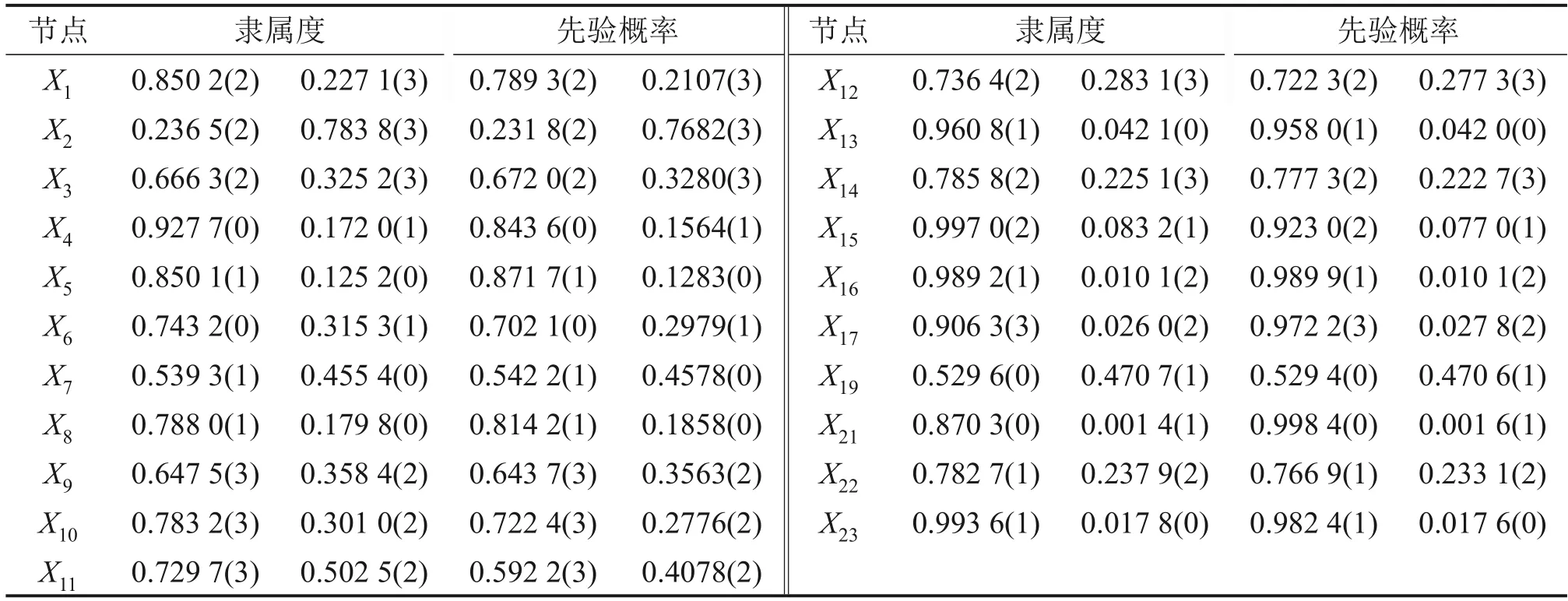
表6 根节点事件先验概率Table 6 Prior probability of root node event

2.3.2 条件概率确定

根据图3中贝叶斯网络中的节点关系结构，邀请广西工程技术研究设计院的1 位地质专家、1 位路桥专家、1 位岩土专家以及2 位安评师对基本节点事件进行两两重要性判断后得到各节点事件的权重如表7。

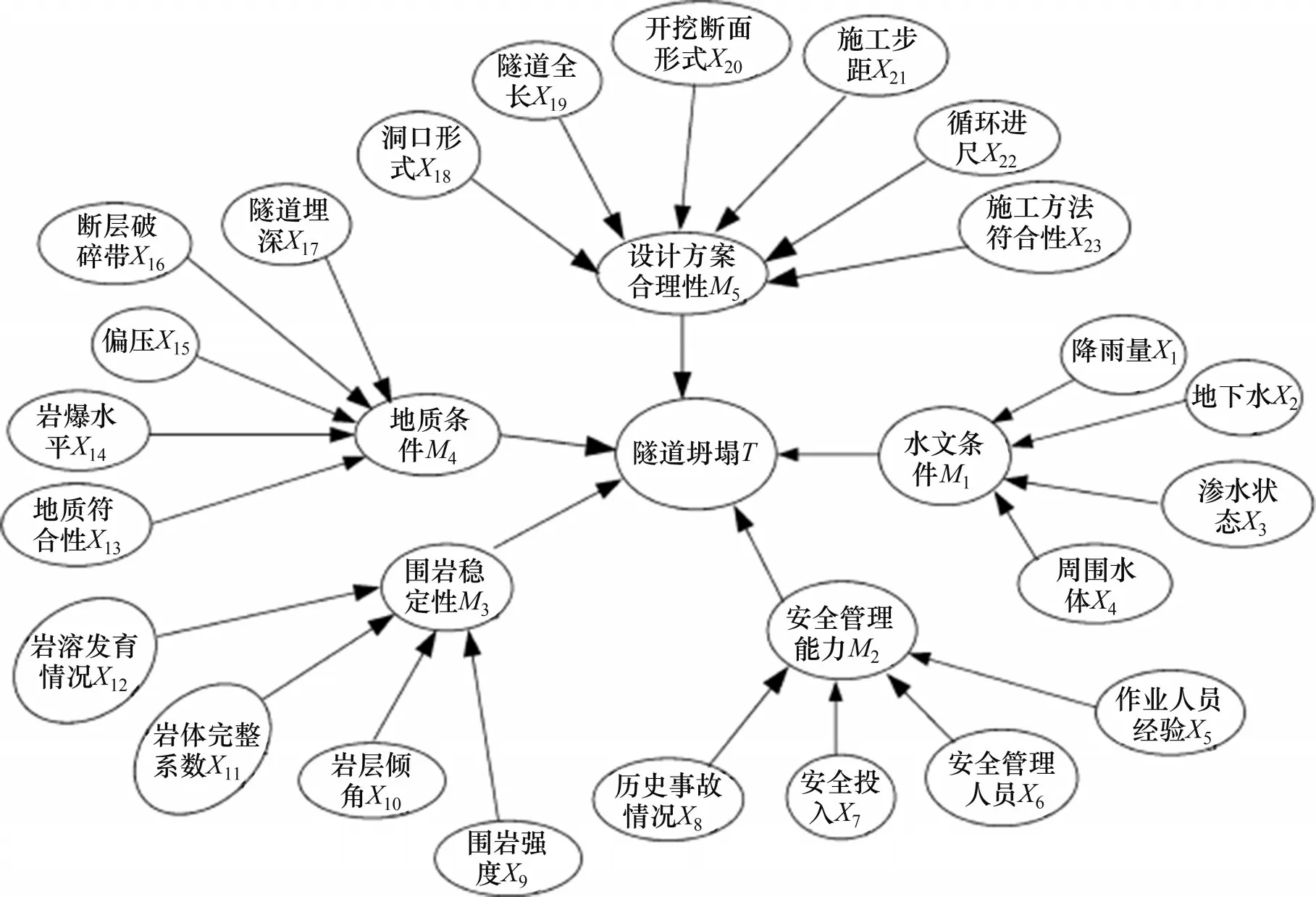
图3 隧道坍塌风险评价贝叶斯网络结构图Fig.3 Bayesian network structure diagram for risk evaluation of tunnel collapse

邀请5位专家对根节点全部处于同一安全状态这种特殊状态组合的条件概率识别框架进行决策判断，建立知识矩阵。按照式(9)求出知识矩阵的最大特征值对应的特征向量将其作为识别框架的基本概率分配函数，利用式(7)对5位专家决策的基本概率分配函数进行融合，按照式(8)求出识别框架中各元素最终的概率分配值，作为条件概率，表8所示为专家对叶节点T与其父节点M1，M2，M3，M4，M5间条件概率决策后计算出的同一安全状态下的条件概率。结合表7中的基本权重按照式(10)求得各父节点的条件概率的状态危险贡献值，由式(11)可求出所有状态组合下的条件概率。

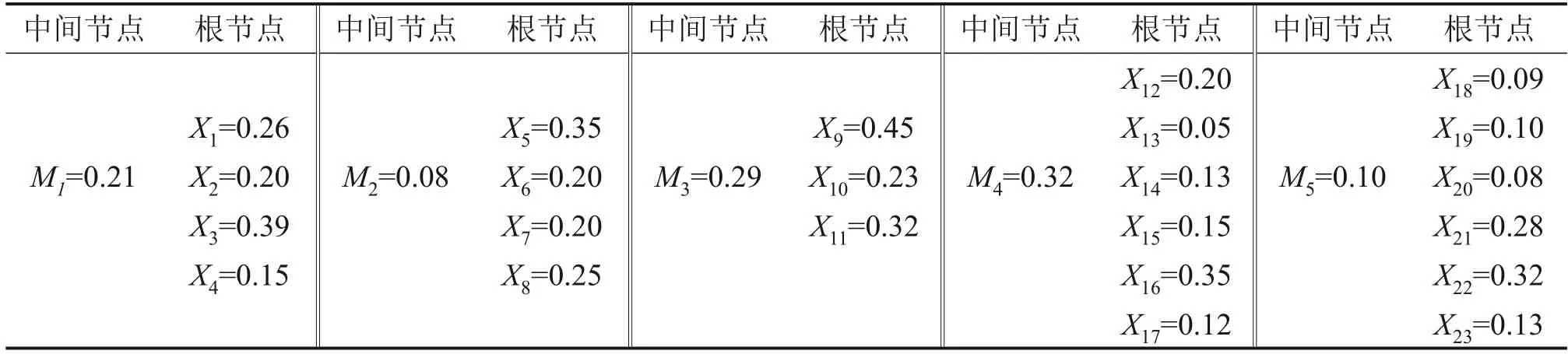
表7 节点事件权重Table 7 Weight of node event

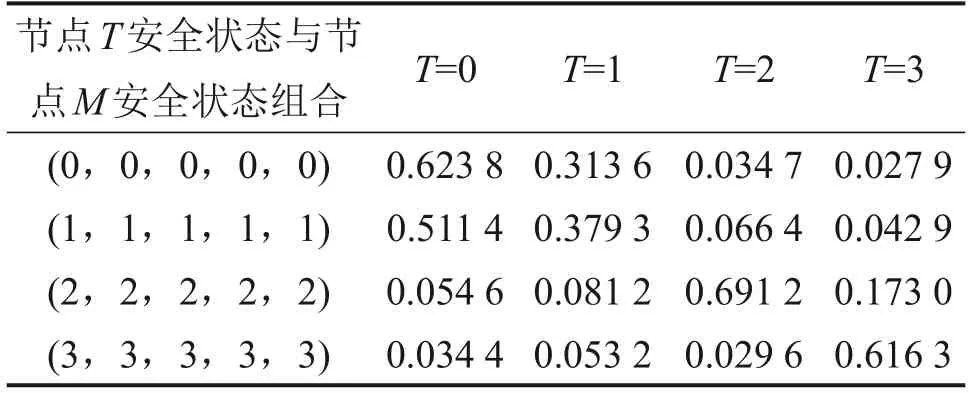
表8 节点T与M间特殊状态组合条件概率Table 8 Conditional probability of special state combination between nodes T and M

2.4 隧道坍塌风险评价结果及分析

按照“公路桥梁和隧道工程施工安全风险评估指南(试行)”标准将隧道坍塌严重程度划分为4级，隧道坍塌发生概率也分为4个级别，按照坍塌严重程度与风险发生概率的组合，将隧道坍塌风险等级划分为四级：低度(Ⅰ级)、中度(Ⅱ级)、高度(Ⅲ级)、极高(Ⅳ级)，见表9。

依据表9的分类标准，将贝叶斯网络叶节点的4 种安全状态与标准中的4 种划分等级进行对应，根据基本事件先验概率以及改进的条件概率，依据贝叶斯网络正向推理式(12)计算得到中间节点事件的发生概率以及隧道不同坍塌程度的风险概率如表10所示。

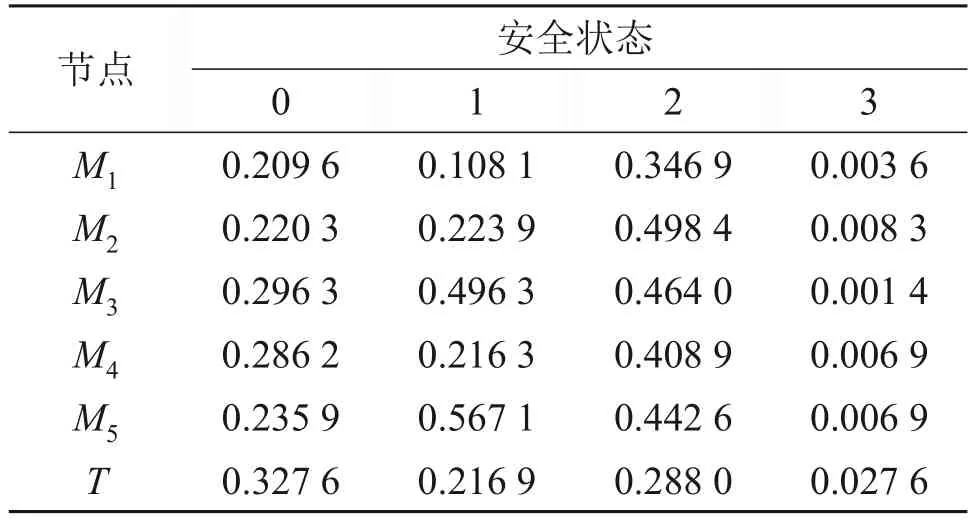
表10 节点M和T的风险概率Table 10 Risk probability of nodes M and T

依据表9 的隧道坍塌风险等级划分标准，4 种坍塌破坏程度与其对应的发生概率组合所得的风险等级均为高度风险(Ⅲ级)，且发生轻微程度的坍塌和发生较大程度坍塌风险的概率较大，分别达0.327 6 和0.288 0，为可能发生的概率区间，由此可得到该隧道坍塌的风险为高度风险水平，需采取风险消减措施以降低安全风险，评价结果与老山隧道坍塌专项风险评估结果以及现场实际开挖情况一致，通过现场的详细勘察发现，在现场开挖的过程中，新开挖的掌子面不稳定，掉块现象频繁且较严重，破坏工作面以及砸伤施工人员，这与评价结果中的发生轻微坍塌的风险等级一致；当开挖面临近断层破碎带、或有岩体破碎、节理发育、地下水作用等不良地质因素影响时，隧道多次发生局部坍塌，围岩变形量大幅超过安全值，局部初期支护结构变形严重，给隧道施工带来极大的影响。

表9 风险等级划分表Table 9 Classification of risk levels

对隧道坍塌事故原因进行诊断有利于辨别安全管控的重点，从而有效地预防隧道坍塌事故的发生，利用贝叶斯网络的反向推理可进行事故原因诊断。依据表10 中隧道发生较大程度坍塌所计算出的概率作为条件，根据式(13)进行贝叶斯网络反向推断，计算隧道坍塌处于状态2且发生概率为0.288 0 时，各根节点事件处于最危险状态的后验概率，结果见图4。

由图4 可见：统计概率为可能发生(≥3%)区间及以上的节点事件进行排序，节点事件的发生概率由高到低排序为X16，X9，X22，X21，X23，X2，X4，X15，X12和X3，因此，隧道施工安全管控的顺序应照此顺序进行。断层破碎带X16、围岩强度X9、施工开挖循环进尺X22、施工步距X21这4种事件对应的后验概率较大，是导致隧道发生较大程度坍塌事故的致因组合，因此，上述4种事件应作为隧道施工中的重点安全管控事件。

图4 根节点事件后验概率Fig.4 Posterior probability of root node event

为了验证改进的条件概率求解方法的准确性，将该方法与全部利用专家决策求得条件概率的传统方法计算出隧道不同坍塌程度的风险概率进行比较，其结果如图5所示。

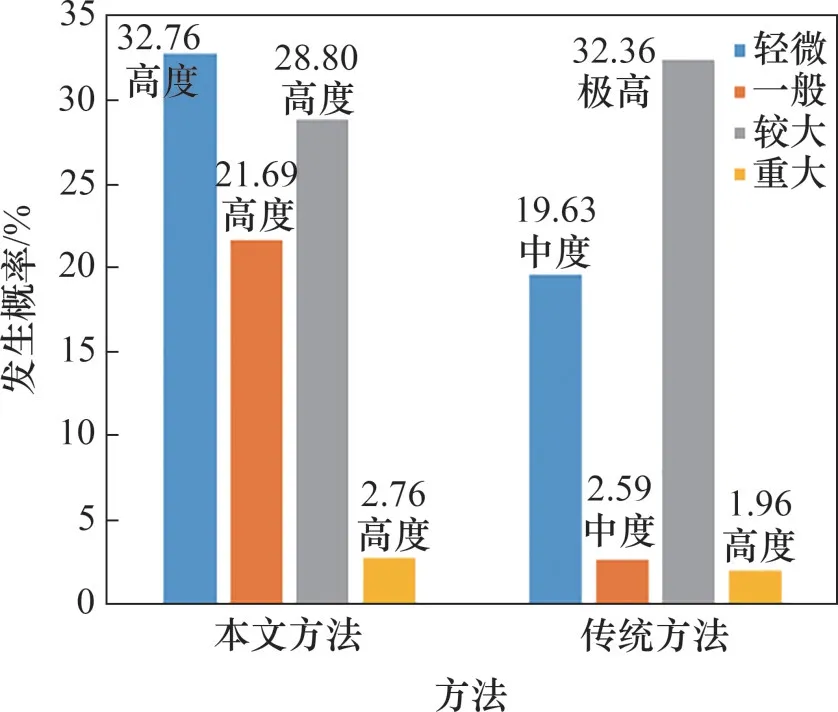
图5 2种方法的隧道坍塌风险概率Fig.5 Tunnel collapse risk probability of two methods

传统方法即所有的条件概率结构由专家进行一一决策，且对多位专家的决策意见利用求和平均的方式进行综合。由图5 可以看出：2 种方法的结果存在较大差异，本文方法计算出隧道发生轻微坍塌的概率最高，而传统方法则是发生较大坍塌概率最高；本文方法计算得到的隧道坍塌风险评价结果为4种坍塌程度风险级别均统一为高度风险(Ⅲ级)，与实际相符；而传统方法的结果为轻微坍塌和一般坍塌处于中度风险(Ⅱ级)，较大坍塌处于极高风险(Ⅳ级)，严重坍塌处于高度风险(Ⅲ级)，最终的结果偏向于中度风险(Ⅱ级)。

由结果可知，传统方法的评价结果离散性大且趋向于中度风险(Ⅱ级)，这与实际不符，造成评价结果离散型较大的原因是因为专家的决策次数过多，不同的专家对同一状态的决策结果相差较大且没有对相差较大的结果进行分析并剔除其中的不良决策结果，导致专家决策信息冗余、错乱，误差较大。本文方法计算条件概率时所用专家决策次数少，主观误差小，且运算步骤更为简单，计算效率大幅提高。

3 结论

1)改进了贝叶斯条件概率的求解过程。将能够对决策对象表达偏好信息的知识矩阵引入专家决策的过程中，将各位专家提供的知识矩阵作为主观条件概率信息的提取手段与信息载体，选取同一安全状态组合情况下的条件概率进行决策，并结合DS证据理论对专家决策信息进行融合，提出一种结合权重与状态危险贡献值的方法确定条件概率。

2)将风险评价方法应用到本工程，确定该隧道的坍塌风险程度级别为高度风险(Ⅲ级)，得到的结果与实际情况以及该隧道开挖坍塌风险评估报告的结果相吻合，验证了该概率计算方法的可行性。通过反向推理进行坍塌事故原因诊断，确定断层破碎带、围岩强度、施工开挖循环进尺、施工步距事件是导致隧道坍塌的主要致因组合。

3)将本文方法计算的概率结果与传统方法计算的结果进行了对比分析，结果表明本文方法在减少专家决策次数、降低主观性、提高计算效率的同时，准确性也更高。