考虑间断级配的破碎矸石压实和再破碎研究

张天军，王小军，庞明坤，张硕，王飞

(1.西安科技大学 安全科学与工程学院，陕西 西安，710054；2.西安科技大学 理学院，陕西 西安，710054；3.陕西彬长文家坡矿业有限公司，陕西 彬州，713504)

充填材料的压实和再破碎特征是影响采空区充填效果和质量的重要因素，采空区的充填效果控制着上覆岩层移动与地表沉降[1-3]。矸石作为一种散体材料[4]，其级配是影响矸石压实特性的重要因素。采矿过程的破碎矸石、掺砾黏土等均处在一种间断级配状态[5-7]。间断级配是指缺少某一个(或几个)粒径区间颗粒而构成的一种级配[8]。关于连续级配岩石颗粒，郁邦永等[9-11]发现，级配颗粒的幂指数越大，被压碎的岩石颗粒越多；张吉雄[12]得到了应变、压实度与应力的关系；张德辉等[13]发现连续级配煤矸石的压缩率与轴压、侧压曲线近似满足指数关系；马占国等[14]通过试验得到了轴向应变、横向应变、泊松比、弹性模量等参数的变化规律；张天军等[15-16]发现随着环境湿度增大，承载能力下降，级配指数越大，则破碎率变化幅度越大。

对于间断级配岩石颗粒的研究目前大多集中在渗透不稳定性方面[17-19]。ⅤENUDHARAN等[20]发现当混合料中粗细颗粒配比合理时，可以提高级配结构的抗压强度。OLARD[21]认为减少中间颗粒的数量，降低细颗粒平均粒径与粗颗粒平均粒径的比值可以减小混合料的孔隙率，并将该理念应用于路面沥青混凝土的设计中；张冬梅等[22]针对间断级配砂土中管线破损引起周围土体的渗流侵蚀等问题，分析了地下空洞产生的原因及颗粒流失的发展规律；杨阳等[23]利用侵蚀柱体在溶解过程中侵蚀管涌通路，发现随着侵蚀过程加剧，砂土的剪切波速逐渐降低，且降低幅度随围压和密实度的增大而增加；刘国耘[24]认为以连续级配的集料为骨架，并用连续级配的细集料填充间断级配料的孔隙，可以形成一个高密度结构。

学者们对间断级配颗粒的研究多是基于渗透不稳定性方面的试验研究，对级配散体颗粒侧限压实和再破碎特征之间的内在机理分析较少。本文针对连续级配及间断级配的破碎颗粒矸石，采用分级加载方式进行侧限单轴压缩试验，研究级配破碎矸石的压实及其再破碎特征；依据实验结果并结合前人研究成果，利用极限法求出极限位移和极限压实度，通过消参法分别建立压实度增量和分形维数、应变和分形维数增量之间的数学模型，并以极限法确定公式中参数的物理意义，据此探讨侧限压实和再破碎之间的内在关系。

1 破碎颗粒压实变形再破碎过程

对于单一粒径岩石破碎体而言，其破坏类型主要分为破裂、破碎和研磨3种，破坏后变为更小的椭球状或粉末状颗粒，如图1所示。

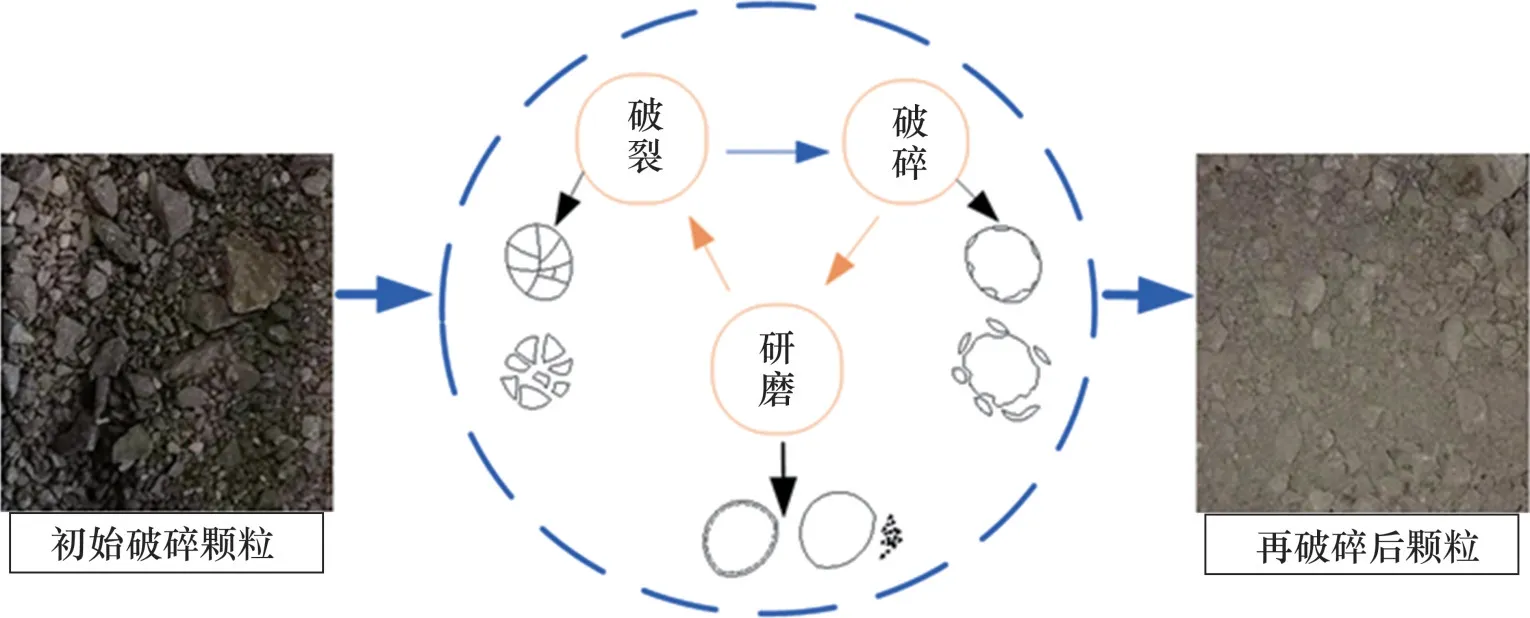
图1 颗粒破碎模式Fig.1 Particle breakage pattern

初始状态的破碎岩石颗粒基本呈棱台状或者锥形状，且棱角分明，其形状特征明显且多元化。对于骨架结构棱角较为尖锐的锥形状，在承压过程中，颗粒之间发生点接触并造成应力集中，最终导致颗粒棱角的脱落，脱落后的细小颗粒填充到大颗粒之间的空隙中。对于棱台状颗粒，在外载荷作用下发生破裂变为较小的颗粒，骨架的破坏使得外载荷直接作用在较小的破碎颗粒上，造成缸筒内岩石颗粒的空隙减小，破碎岩石颗粒之间变得更为密实。此时，较小颗粒相对于细小颗粒而言承担了骨架角色，在外载荷不断作用下，破碎颗粒不断发生破裂、破碎、研磨一系列复杂的变化，使大颗粒变成椭球状或粉末状。因而，在缸筒内对破碎岩石颗粒进行承压压实试验时，发生二次破碎，破碎的主要形式为骨架的破坏和非骨架中细小颗粒的研磨破碎。

从破碎岩石颗粒组成的宏观系统来看，破碎岩石颗粒在缸筒中进行压缩试验过程中，主要表现为整个破碎岩石试样轴向位移和体积的变化，如图2所示。图2中，h0为试样初始高度，h为承压过程中试样高度，hlim为完全压实后试样高度。

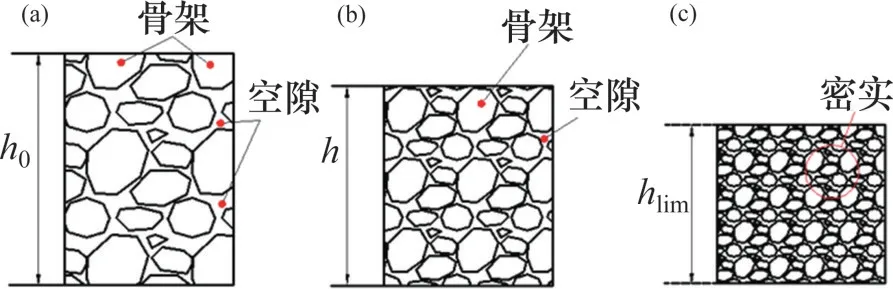
图2 破碎岩体压实过程Fig.2 Compaction processes of fractured rock mass

在载荷作用下，一定质量的破碎岩石颗粒主要表现为试样轴向位移增大，体积不断减小。在颗粒填充下破碎试样中较大的间隙填充基本完成，无法再通过颗粒间的移动来减少空隙，此时，在较大的轴向应力下岩石颗粒发生破碎、破裂、研磨等，使大颗粒变成较小颗粒填充到剩余的空隙中，从而减小破碎煤岩体的空隙，使其进一步压实。当颗粒间的孔隙小到一定程度时，破碎煤岩体在高应力的作用下发生固结、黏结等效应，使级配破碎岩石颗粒被压实成为接近原岩体的类原岩体。空隙的不断减小以及骨架占比不断增大，导致级配岩石颗粒的骨架作用不断增强。因而，该过程也是一个级配破碎岩石颗粒抗压缩能力不断增大的过程。

2 试验方法

2.1 试验设备

采用DDL600破碎岩石压缩系统进行试验，它是一种多功能岩石力学试验系统，该系统主要用于开展渗流、剪切、单轴压缩等试验。该系统主要包括电子万能试验机DDL600、压实装置、电子分析天平和主控计算机等，如图3(a)所示。其中，破碎岩石压缩装置主要由缸筒、活塞、毛毡等组成，缸筒高度与内径分别为200 mm和100 mm。考虑到试样在受载过程中的径向应变和环形应变会对试验精度产生影响[10]，因而，试验所用缸筒采用刚度较大的钛合金材料，以尽可能提高试验精度。试验前在缸筒内壁及活塞上涂抹润滑油，在后续试验中忽略缸筒与试样接触的摩擦阻力的影响。试样底部装有毛毡，以防止煤矸石样颗粒从底部通口处流出，避免矸石颗粒质量流失对实验结果产生影响。

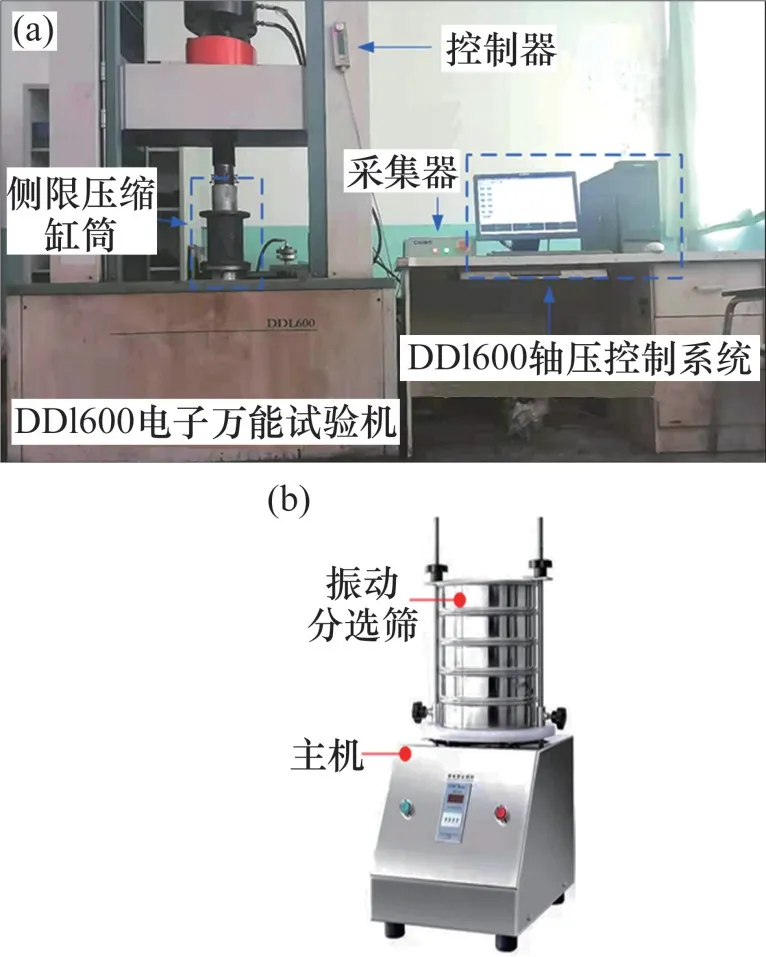
图3 破碎岩体压缩试验设备Fig.3 Crushed rock compression test equipment

2.2 试验原理与步骤

分形维数是表征破碎颗粒粒度分形复杂程度的参数。根据分形维数的基本表达式[10]，饱和破碎岩石颗粒数量与粒径的关系可表示为

式中：x为级配特征粒径即筛孔孔径；d为破碎煤岩颗粒的粒径；N为破碎颗粒的直径小于等于d的破碎颗粒数量；C为特征常数；D为分形维数。根据破碎煤岩体的颗粒质量M与特征尺度的关系，M∝d3，破碎颗粒中粒径小于d的颗粒质量Md可以表示为

式中：λ为破碎煤岩颗粒的形状系数；ρ为岩石颗粒密度；dmin为破碎颗粒的最小粒径。将式(1)代入式(2)，记破碎煤岩体的最大颗粒粒径为dmax，则破碎煤岩体颗粒的总质量Mt表达式为

根据式(3)可得到破碎颗粒中的粒径小于d的颗粒质量Md与试样整体总质量Mt的比值，其表达式如下：

破碎煤岩体在轴向应力作用下，颗粒之间会发生研磨并产生一些粉末状的颗粒，与破碎试样颗粒中最大粒径的颗粒相比，最小粒径dmin可定义为0 mm，则式(4)可以进一步表示为

对式(5)两边同时取对数可得：

本次破碎煤矸石加载试验通过破碎岩石筛分装置选取颗粒粒径分别为(0～5]，(5～10]，(10～15]，(15～20]，(20，25]mm 的5 组煤矸石原料。根据连续级配理论，取幂指数n=0.2，0.4，0.6 和0.8，在不同n下均配制3组试样，1组为连续级配试样，其余2组为间断级配试样，每组试样采用4级应力分级加载，应力分别为2，4，8和12 MPa。每组试样质量为1 000 g。将每组试样分别装入不同的容器盒，并进行编号。加载方式设置为应力加载，加载速度设置为0.05 MPa/s。为使试样充分变形和破碎，试样加载到某一级应力后，应力保持时间设置为30 min。为避免人工筛分所引起的误差，采用破碎煤岩体自动筛分装置筛分得到再破碎后煤矸石的不同粒径区间颗粒。根据试验所选筛网，按照颗粒粒径，依次在自动筛分装置上安装好相应颗粒粒径的筛网，并将筛网固定，如图3(b)所示。然后，在最上层装入破碎矸石颗粒，然后开启电源开关，运行5 min即可保证颗粒被充分筛分。

2.3 试样配制

连续级配曲线和间断级配曲线示意图如图4所示，以连续级配为基准，间断级配曲线可以看作是在基准级配上剔除某一粒径区间颗粒所形成的级配曲线。其中，w为细料质量分数；di为间断粒径区间中颗粒粒径最小值，mm，dj为间断粒径区间中颗粒粒径最大值，mm。

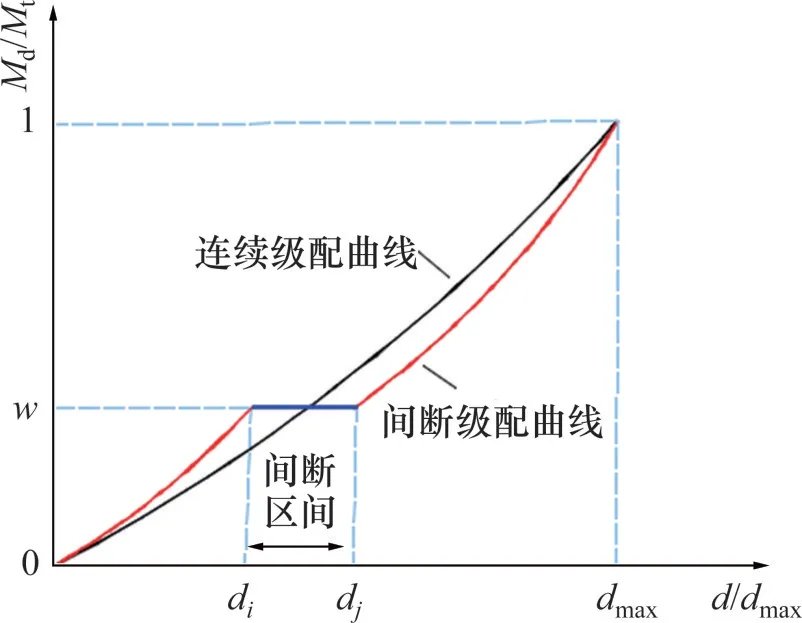
图4 级配曲线示意图Fig.4 Diagram of gradation curve

为后续绘图和分析方便，下文中出现的间断区间di～dj是指级配中缺失矸石颗粒粒径d大于di而小于等于dj。例如，间断区间0～5 mm，即指级配中缺失粒径大于0而小于等于5 mm颗粒所构成的级配。

采用连续级配理论配置不同幂指数n下连续级配试样，根据Talbot 级配公式[9]计算总质量为1 000 g的各粒径区间质量。

连续级配下破碎矸石颗粒质量分布如表1所示。

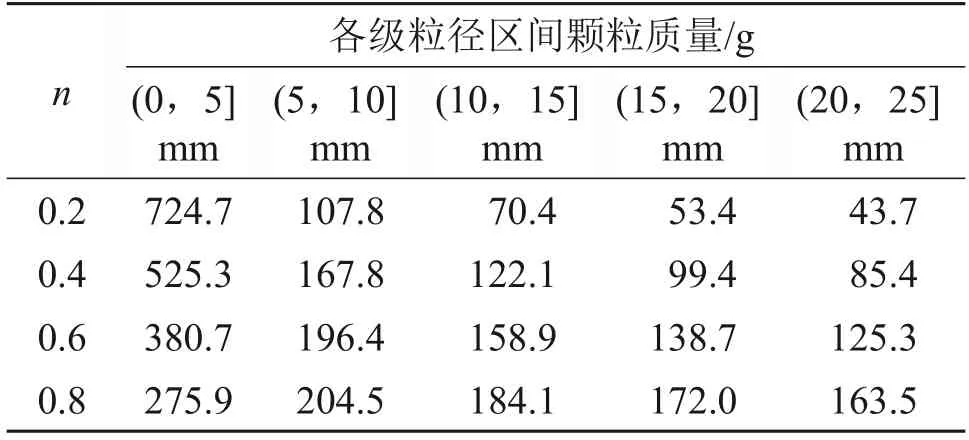
表1 连续级配颗粒质量分布Table 1 Mass distribution of continuous gradation particle

间断级配试样与连续级配试样质量相同，基于等比放大原则，每个幂指数n下设置间断0～5 mm粒径颗粒和间断15～20 mm粒径颗粒两种级配结构。本文定义粒径在0～5 mm范围内的颗粒为细粒，粒径的颗粒大于5 mm为粗粒。设细料质量为Ms，粗料质量为Ml，则细料质量分数w可以由下式确定：

间断级配下各粒径区间颗粒质量分布如表2所示。

表2 间断级配颗粒质量分布Table 2 Mass distribution of missing gradation particles

3 级配破碎矸石变形压实特性

3.1 轴向位移-轴向应力曲线

轴向位移s可通过计算试样各级应力作用下的高度h和初始试样高度h0之间的差值求得：

破碎矸石在带侧限的缸筒中受侧向约束，因为缸筒刚度较大，其径向变形可以忽略不计，所以只产生轴向应变。轴向应变ε是指任一级轴向应力作用下，轴向位移和试样初始高度的比值：

郁邦永等[10]通过实验发现连续级配破碎岩样轴向位移s与轴向应力σ之间满足负指数函数关系：

式中：a1和b1均为拟合参数。对式(11)两边同时除以h0后即可得到应变和应力的关系：

对式(12)求导即可得到压缩模量ES：

从式(13)可以看出，当轴向位移s趋于a1时，压缩模量趋于无穷大，这表明a1即为极限位移。

根据试验结果，绘制不同级配破碎矸石的轴向位移-轴向应力曲线，见图5。由于拟合结果中b1是一个负值，对式(11)中的轴向应力取极限值，即可得到极限位移slim：

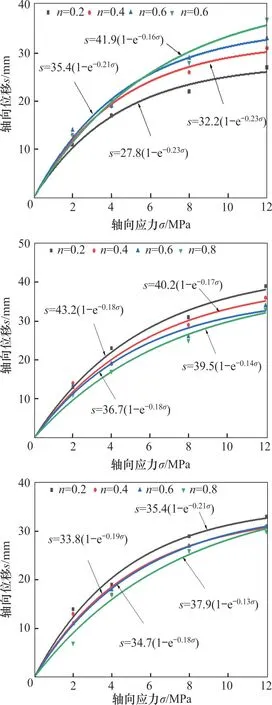
图5 试样轴向位移-轴向应力曲线Fig.5 Axial displacement-axial stress curve of samples

从式(14)可以得知轴向位移随轴向应力变化呈现出收敛特性，b1越小，则收敛速度越快，即相应级配轴向位移随应力变化趋于稳定的速率更快。

从图5可看出，轴向位移与轴向应力符合指数函数关系，且相关系数在98%以上，表明式(11)对连续级配和间断级配试样均适用。随轴向应力增加，轴向位移呈增加趋势。当应力为0～4 MPa 时，位移处于快速增加阶段，当应力大于4 MPa时，位移处于缓慢增加阶段；大约60%的位移增量发生在快速增加阶段。对于连续级配试样，幂指数n越大，极限位移越大。对比图5(a)和(b)可知，间断0～5 mm粒径级配试样整体位移较大。这是因为主导位移增量的主要阶段是快速变形阶段，破碎矸石压实过程中位移的变化主要是以移位重组填补空隙为主，大粒径颗粒质量越大，颗粒之间的初始空隙大，因而产生的变形大。

3.2 级配结构抗压缩性能分析

当n=0.2 时，连续级配试样在轴向应力σ分别为0，4和12 MPa下的颗粒压实状态实物图见图6。从图6可以看到：破碎矸石在轴向应力作用下，颗粒棱角脱落，变得光滑，颗粒粒径不断减小。颗粒与颗粒之间由松散状态逐渐变为密实状态，颗粒与颗粒之间的嵌合程度随之增强。

图6 不同轴向应力下的矸石颗粒压实状态实物图Fig.6 Physical diagrams of compaction state of gangue particles under different axial stresses

为考察压缩模量的变化，根据式(13)绘制压缩模量和轴向应力的曲线，如图7所示。

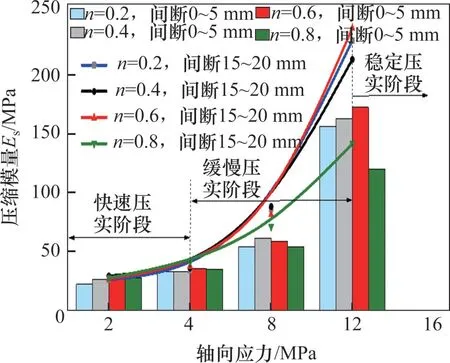
图7 压缩模量-轴向应力曲线Fig.7 Compression moduli-axial stress curve

从图7可看出，当应力为0～4 MPa时压缩模量小于50 MPa，压缩模量随轴向应力的变化呈缓慢增大趋势，此阶段试样处于快速压实阶段，应力卸除后具有较强的弹性效应，压缩模量随轴向应力变化近似呈线性关系。在快速压实阶段，轴向应力所做的功主要用于克服颗粒与颗粒之间的摩擦力，且应力集中在空隙附近，当空隙附近的应力超过静摩擦力，将引起空隙附近的局部失稳，即颗粒克服内摩擦力填充到空隙中或导致颗粒与颗粒之间的嵌合。

当应力为4～12 MPa 时，压缩模量随轴向应力的增大而快速增加，级配试样抗压缩能力显著增强，此阶段压缩模量随轴向应力的变化呈现出快速增大趋势。试样变形速度逐渐变缓，处于缓慢压实阶段。这是因为经过快速压实阶段，试样内的空隙被压缩及其内部结构调整优化，大颗粒的骨架作用不断增强，承载骨架中的颗粒由于应力集中而产生大量破碎，破碎的小颗粒填充到空隙中，进一步减小了空隙，试样承载能力大幅提升。此阶段试样变形表现为应变硬化特性，具有较强的塑性。在塑性变形阶段散体颗粒压缩模量与塑性应变之间呈显著的非线性相关关系。

当应力大于12 MPa 后，压缩模量整体上大于100 MPa，此阶段试样形成相对稳定的骨架承载结构，大颗粒被小颗粒紧密包围，降低了压实过程中应力集中效应，较大颗粒很难发生再破碎。因而，承载骨架发生失稳破坏的可能性较低，主要以结构微调、骨架优化为主。此阶段级配试样稳定性越来越强，处于稳定压实阶段，破碎矸石岩体成为接近原岩体的类原岩体。根据文献[25]可知，当研磨小颗粒足够多，使得大颗粒被小颗粒包围而处于“悬浮”状态时，可能会导致级配承载能力下降。

对于深部矿井精准充填，需要考虑高应力时的压实情况。因此，采用极限位移分析不同级配的极限压实度。压实度可用来表征试样在外力作用下的压实程度：

式中：K为压实度；V2为压缩后的体积；V1为压缩前的体积。由于缸筒底面积恒定，因而压实度K可简化为

由式(9)，(14)和(16)可推导出压实度的极限值Klim为

为考察不同级配试样的抗压缩性，定义压实度极限值大于0.7即高应力作用下变形不超过30%的级配试样具有较强的抗压缩性能。根据式(17)绘制出压实度极限值Klim与Talbot指数n之间的关系，如图8所示。

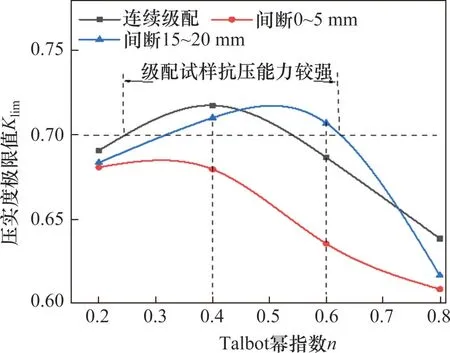
图8 压实度极限值-Talbot指数曲线Fig.8 Limit-Talbot exponential curve of compactness

由图8 可知，间断0～5 mm 级配试样压实度极限值Klim随n增大而减小，连续级配和间断15～20 mm级配试样压实度极限值随n增大呈现出先增后减的趋势。当n=0.4时，连续级配试样具有最大极限压实度，表明其抗压缩性最强。当0.4＜n＜0.6时，间断15～20 mm级配试样压实度极限值大于0.7且存在最大值，表明此阶段级配试样具有良好的抗压缩性，结合表2 和式(8)，可知级配结构中0～5 mm 细颗粒质量分数为44.2%～58.3%。间断0～5 mm粒径级配结构压实度极限值始终小于0.7，抗压缩性最弱。这说明，对于压实性而言，级配结构中缺失小粒径颗粒比缺失中间粒径颗粒的影响大得多，缺少中间粒径的颗粒，颗粒级配结构的压实度可能会提高，这与于际都等[25]的结论相符。

4 级配粒径分布及其分形特征

4.1 粒径区间分布

为研究破碎矸石压实过程中缺失小粒径和缺失中间粒径颗粒对破碎矸石再破碎特征的影响，根据实验结果绘制出间断0～5 mm和间断15～20 mm级配压实过程中各个粒径区间所含颗粒质量分数wp与轴向应力σ之间的关系，如图9所示。

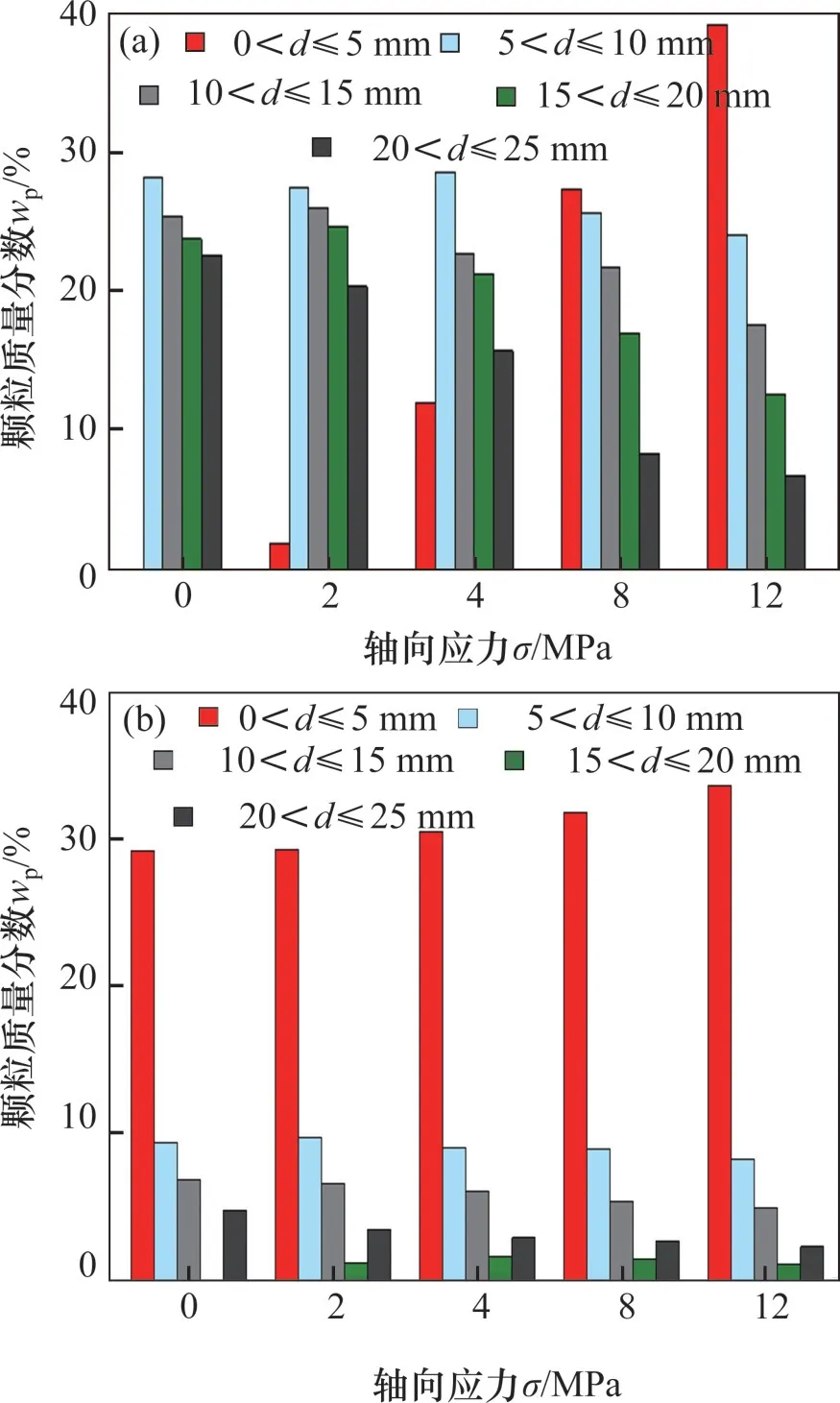
图9 颗粒质量分数-轴向应力关系Fig.9 Relationship between particle mass fraction and axial stress

从图9可看出，破碎矸石压缩过程中主要表现为大粒径颗粒质量分数不断减少，小粒径颗粒质量分数不断增大。从颗粒粒径迁移角度来讲，随轴向应力增大，大粒径区间颗粒不断发生破碎后迁移到小粒径区间，初始间断级配中间断区间的颗粒得以补充。当0＜σ≤4 MPa 时，间断0～5 mm 级配中0～5 mm 粒径的小颗粒质量分数增加了11.9%；间断15～20 mm的级配中0～5 mm粒径的小颗粒质量分数增加了2.8%。当4＜σ≤12 MPa 时，间断0～5 mm 的级配中0～5 mm 粒径的小颗粒质量分数增加了27.4%；间断15～20 mm的级配中0～5 mm的小颗粒质量分数增加了6.2%。即间断0～5 mm 级配中0～5 mm小颗粒质量分数相较于间断15～20 mm级配中0～5 mm小颗粒质量分数增加幅度大。这表明缺失小颗粒，级配更易发生再破碎，且试样中颗粒的再破碎主要发生在缓慢压实阶段(4＜σ≤12 MPa)。

4.2 分形维数变化

依据式(6)可求得lg(Md/Mt)与lg(d/dmax)的关系，其斜率为3-D，从而可求得D。郁邦永等[9]通过实验得到连续级配破碎样分形维数与轴向应力之间的关系式：

式中：a2，b2和c2均为拟合参数。

为考察不同级配结构的试样在不同轴压下分形维数的变化情况，这里以n=0.2时的3组试样结果为例，绘制分形维数D与轴向应力的关系，如图10所示。由图10 和式(18)可知，本文b2为负数，对式(18)中的轴向应力取极限值，则分形维数随轴向应力变化趋于c2，b2越小，趋于c2的速度越快。

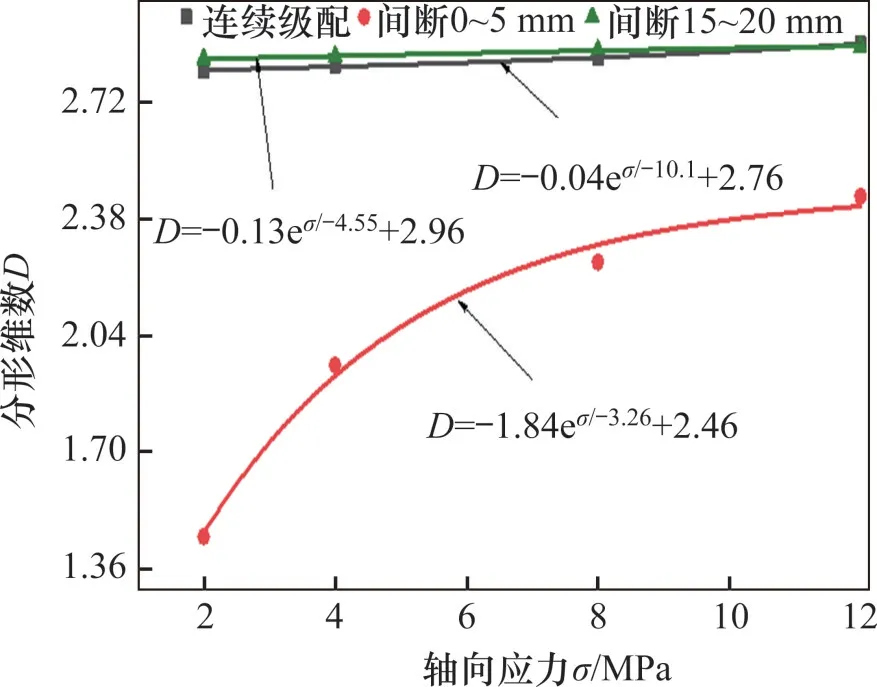
图10 分形维数-轴向应力曲线Fig.10 Fractal dimension-axial stress curve

由图10可以看出，式(18)拟合结果与实际结果一致性高，相关系数在99%以上。整体上，连续级配和间断级配下试样分形维数均随轴向应力的增加而增加，这是由于不同级配试样在压缩过程中会发生大量颗粒破碎，使不同级配均向着某一最优级配进行演化。间断0～5 mm级配结构的分形维数受轴向应力影响明显，级配稳定性较差；间断15～20 mm级配的粒径颗粒的分形维数随轴压变化较为缓慢。此外，间断0～5 mm级配试样的分形维数始终小于其他2种级配试样的分形维数，而随应力的增加，间断15～20 mm级配试样的分形维数与连续级配试样的分形维数趋于一致，两者之间的差值越来越小。这表明级配中缺失小粒径颗粒对分形维数的影响要比缺失中间粒径颗粒的影响大。

5 压实和再破碎模型及其参数物理意义

级配破碎煤矸石压实和再破碎过程是一个相互作用的动态变化过程。随轴向应力增加，破碎矸石构成的系统体积不断减小，空隙随之减小，破碎矸石不断被压实。从统计学角度来看，矸石颗粒发生再破碎，粒径不断减小，原本处于某一粒径区间的破碎颗粒进行重新分布，因而破碎矸石颗粒的压实过程也是一个颗粒再破碎和粒度分形演变过程，两种动态变化过程必然存在某种潜在关系。

HARDIN[26]认为随着轴向应力的增加，大粒径颗粒会完全发生破碎，直到所有颗粒粒径均小于0.074 mm，此时级配曲线会成为一条水平线；基于此理论，提出了破碎度指标Br即破碎度Bt与破碎势Bp之间的比值，其中破碎度Bt反映了当前颗粒级配曲线与破碎前初始级配曲线所围面积，破碎势Bp反映了初始级配曲线与水平线所围面积，如图11所示。

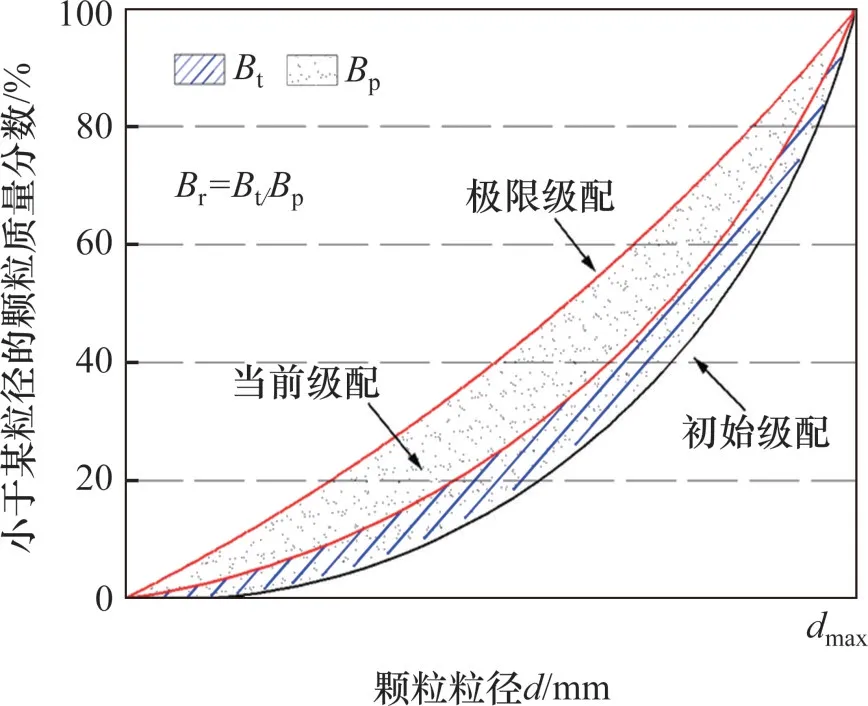
图11 破碎度示意图Fig.11 Schematic diagram of crushing degree

陈子玉等[27]对破碎度指标进行了修正，认为具有分形级配的堆石料，其破碎度指标仅与初始分形维数D0、当前分形维数D、分形维数极限值Du相关，并给出了计算公式：

由式(19)可知，求取极限分形维数是准确计算任一轴向应力作用下的破碎度指标的关键。为进一步探讨破碎矸石侧限压实和粒度分形之间的内在机理，并求取极限分形维数，可从压实度和分形维数之间的定量关系进行分析。将式(9)和(11)代入式(16)可以得到压实度和轴向应力之间的关系：

从图10可知式(18)可以有效预测级配破碎矸石分形维数和轴向应力之间的关系，故结合式(18)和式(20)，消去应力σ，可得到表征破碎矸石压实程度和分形变化的压实-分形模型：

为简化式(21)，定义任一轴向应力作用下的压实度和压实度极限值两者之间的差值为压实度增量ΔK：

结合式(17)和(22)，整理并简化得：

其中：

式中：a1，a2，b1，b2和c2均不等于零。

为分析压实度增量和分形维数之间的变化规律，选取n=0.2时3种不同级配下ΔK的实验值和理论值进行对比，如图12所示。

从图12可看出，随着分形维数增大，压实度增量ΔK不断减小。ΔK实验值和理论值之间存在相似变化趋势，且实验值和理论值之间的相对误差小于10%，再次证明式(11)和式(18)在一定误差允许范围内的合理性，也说明由式(23)所表征的压实-分形模型的有效性。ΔK理论值和实验值存在误差，主要是颗粒分形统计过程中颗粒形状的不规则性和筛选规则存在差异以及小部分颗粒质量流失造成的。此外，式(11)和式(18)的拟合精度也是造成误差的重要原因。

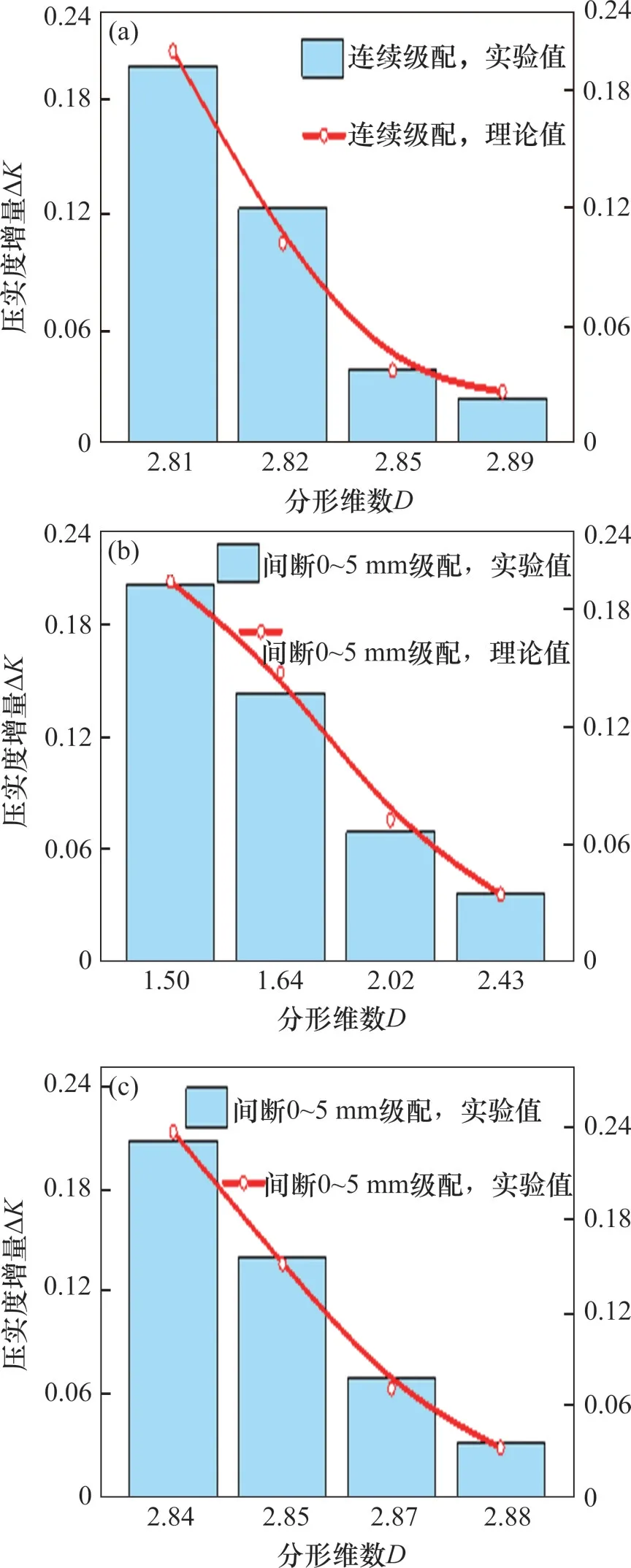
图12 压实度增量-分形维数关系Fig.12 Relationship between fractal dimension and degree of compaction

对于式(23)，根据拟合参数计算得知a和b均不为零，且压实度增量ΔK是一个非负数。因而，有且只有当D等于c2时，ΔK取得最小值，且最小值为零。这表明只有当分形维数D等于c2时，才满足压实度和极限压实度之间差值为零的条件。压实度和压实度极限值之间的差值反映了级配破碎矸石的压实潜能，当压实度等于压实度极限值时，试样被完全压实。在稳定压实阶段，压实变形主要是以结构微调、骨架优化为主，大颗粒很难发生再破碎，当轴向应力足够大时，可以认为试样被完全压实，破碎终止。由式(19)可知，分形维数的变化表征级配的破碎度变化，随着分形维数增大，破碎度也随之增大。当分形维数趋于分形维数极限值时，破碎度达到极限值，即此时破碎试样组成的系统内不再发生颗粒的再破碎，达到一种理想状态下的稳定结构，由此，可得不同级配矸石再破碎后粒度分形维数极限值Du：

将式(18)和(25)代入式(19)得到关于任一轴向应力作用下破碎度Br的计算公式：

从式(26)可知，对于初始分形维数确定的侧限压实条件下的级配，破碎度指标只和轴向应力有关。破碎度随轴向应力的增大而增大，当破碎试样的当前分形维数趋于分形维数极限值时，破碎试样的再破碎程度也达到极限值1。

文献[28]中将堆石料颗粒发生破碎后的分形维数和破碎前的分形维数差值定义为级配散体颗粒的破碎率。据此，本文将极限级配状态和初始级配状态所对应的分形维数极限值和初始分形维数之间的差值定义为破碎潜能，即分形维数增量ΔD：

结合式(18)，(25)和(27)可以得出：

根据应变式(10)和极限位移a1，得出极限应变εlim为

式(12)是由式(11)变形所得，因而结合式(28)可将式(12)变形为

将式(28)和(30)两边同时相除，消去中间变量σ，结合式(24)整理并简化，得到压实-再破碎关系式：

式(31)左边表征级配再破碎特性，右边表征级配压实特性，且颗粒破碎随应变变化呈现出收敛特性。在初始未承载状态，即应变为零时，a2等于分形维数极限值和初始分形维数的差值；在完全压实状态即应变趋于应变极限值时，分形维数增量为零，分形维数达到分形维数极限值。因而，对于不同级配破碎矸石，a2的绝对值越大，则表明达到完全压实时，分形维数增量越大(即破碎潜能越大)，级配越不稳定。结合图12中a2的绝对值可知，连续级配结构最稳定，间断15～20 mm粒径级配结构次之，间断0～5 mm粒径级配结构稳定性最弱。

综上可知，对于侧限压实条件下级配破碎矸石的压实和再破碎特性的量化分析，式(11)中a1可表征极限位移，b1表征轴向位移随应力变化趋于稳定的速率。式(18)中的a2可以表征破碎矸石的稳定性，b2表征分形维数随应力变化趋于分形维数极限值的速率，c2表征再破碎后的分形维数极限值。

6 结论

1)级配破碎矸石轴向位移和轴向应力、分形维数和轴向应力之间分别满足不同正相关指数函数关系，且函数均具有收敛性，不同级配对应的函数收敛速度不同。

2)级配破碎矸石的压实阶段可分为快速压实阶段(0＜应力σ≤4 MPa)、缓慢压实阶段(4＜应力σ≤12 MPa)和稳定压实阶段(应力大于12 MPa)。快速压实阶段弹性显著，缓慢压实阶段塑性较强，稳定阶段试样成为接近原岩体的类原岩体。在高应力作用下，当连续级配幂指数n=0.4时，具有较强的抗压缩性；当细料质量分数为44.2%～58.3%时，间断15～20 mm 粒径级配试样具有较强的抗压缩性；间断0～5 mm粒径级配试样抗压缩性能较差。

3)级配破碎矸石破碎度随轴向应力增大而增大，且试样的再破碎主要发生在轴向应力为4＜σ≤12 MPa时即缓慢压实阶段。在同一基准级配下，间断小粒径级配试样分形维数随轴向应力增加变化幅度大，收敛速度快。这说明缺失小粒径颗粒的级配试样更容易发生再破碎，级配稳定性较差。

4)采用表征压实潜能的压实度增量ΔK和表征分形特征的分形维数D，建立了压实-分形关系式，其中，参数c2可以表征不同级配的分形维数极限值；通过表征压实变形的应变和表征再破碎潜能的分形维数增量，建立了压实再破碎关系式，其中，参数a2的绝对值可以表征不同级配的稳定性，连续级配结构最稳定，间断15～20 mm粒径级配结构次之，间断0～5 mm粒径级配结构稳定性最弱。