一种光学短弧初轨确定的轨道偏心率判定方法

张郑元, 李彬,2, 赵广宇,4, 曾春平, 叶钊, 桑吉章,2

(1. 武汉大学测绘学院, 湖北 武汉, 430079; 2. 湖北珞珈实验室, 湖北 武汉, 430079;(3. 航天东方红卫星有限公司 北京 100094; 4. 中国科学院空天信息创新研究院 北京 100094)

1 引言

经典的空间目标初轨确定方法, 如Gauss 法、Laplace 法, 最初是用来解算小行星的轨道。 当其应用于近地卫星轨道的光学初始轨道确定时, 往往不收敛或得不到精确解[1,2]。 随着计算机技术的发展, 如double-r法、 Gooding 法的数值算法的出现, 解决了经典算法针对近地目标光学初轨确定时存在的不易收敛的问题[3-6]。 然而, 由于光学短弧对轨道的几何约束能力很差, 这些数值算法在仅利用3 方向观测值进行短弧初轨解算时,估计精度仍然难以达到应用期望[7,8]。

随着光学观测技术的发展, 光学观测的数十秒至数分钟弧段可能有数十至上百个观测方向,因此可以组成许多3 方向组合。 Henderson 首先使用Gooding 方法解算多组3 方向组合, 然后通过遗传算法挑选出比较好的解算结果取平均作为最终解[9]。 这种做法增强了Gooding 法在光学短弧初轨解算时的鲁棒性, 但由于即使在小偏心率初轨解算时, Gooding 初轨参数集的分布也并非高斯分布, 而在偏心轨道时, 轨道参数估计分布的均值与轨道参数真值之间往往存在显著偏差, 因此最终的初轨参数经常也存在很大的误差。

在处理短弧多方向初轨确定问题时, 章品对弧段的首尾方向的斜距进行网格搜索, 通过由假设斜距所得到的计算观测值与真实观测值之间的差异大小, 来确定多组轨道解, 然后用小偏心率约束, 从多组轨道解中挑选最终解[10]。 这种方法会导致偏心轨道解算结果的误差较大。 因此, 目前迫切需要一种更准确的初轨确定方法, 其应充分利用短弧光学弧段的信息, 且能够自适应各种偏心率下的轨道。

有鉴于此, 本文将提出一种短弧多方向初轨参数确定方法。 首先通过一定策略形成多个3 方向组合, 并用经典的Gooding 方法解算每个3 方向组合的初轨参数, 如果收敛, 则立刻得到一个候选轨道解。 然后, 利用众多待选轨道解的“半长轴-偏心率” 的二维分布特征, 初步确定目标轨道的偏心率, 最后根据初定偏心率从待选轨道解集合中确定最终解。 本文注意到, Gooding 方法在进行光学短弧初轨确定时需要较为精确的初始距离估值, 否则容易造成不收敛的问题。 因此,本文也对距离搜索法的小偏心率约束进行了优化, 使其能够在偏心轨道上也能提供准确的距离。

本文章节安排如下, 第2 节介绍一种改进的距离搜索法, 可以缓解该算法的小偏心率约束准则在偏心轨道上出现大估计偏差的情况。 第3 节讨论Gooding 方法解算3 方向组合所得到待选解半长轴-偏心率的分布与目标轨道真偏心率之间的关系, 并给出一种选解策略。 第4 节开展大规模的仿真实验验证方法的有效性。 第5 节对本文研究进行总结。

2 改进的距离搜索法

假设在观测时刻ti, 传感器与目标之间的关系可用方程(1) 表示, 即:

式中,αi和δi分别表示观测时刻ti对应的“传感器-目标” 之间的赤经和赤纬。

由于距离搜索法采用小偏心率约束准则, 其在小偏心率轨道上具有良好的斜距初值估计精度。 但当其应用于偏心轨道的初始斜距估计时,会出现较大的偏差。 Gooding 方法在使用距离搜索法所提供的斜距初值进行初轨确定时, 在偏心轨道上极易收敛到错误解或不收敛。 因此, 本文根据距离搜索法待选解的偏心率分布特征提出一种修正方法, 以较好估计目标的偏心率大小, 并采用合适的策略选择最终解。

距离搜索法对弧段首尾时刻“传感器- 目标” 斜距ρfore和ρaft进行网格搜索, 通过由假设斜距所得到的计算观测值与真实观测值之间的差异大小, 判别并得到多个待选轨道解[10]。 其中, 一组首尾时刻斜距的网格搜索组合见下式:

由一组可选变量xjk, 便可计算首尾时刻目标对应的目标位置矢量r⇀fore和r⇀aft, 代入Gauss-Lambert 方程, 便可以得到一组轨道根数解[3]。通过轨道根数解和二体方程, 并考虑摄动项, 便可以计算得到目标在观测时刻ti的位置矢量。

那么, 用统计量来描述这些观测资料之间的偏差, 取统计量都满足阈值σn时所对应的xjk计算得到待选的轨道参数解, 待选的轨道解个数表示为Nn, 其中n表示距离搜索法的循环次数。

需要注意的是, 解的个数N0与判别阈值σ0的选择有极大的关系。 低轨目标相比于高轨目标而言, 需要更大的阈值, 才能保证相近的数量级。 其原因在于, 在相同的斜距网格搜索步长下, 当斜距发生一个搜索网格的变化时, 低轨目标所产生的角度观测值变化更大。

为保证不同类型轨道解的个数都能够满足后续轨道特征的分析, 本文采取以下优化措施。 先使用大阈值σ0来确定待选解的数目N0, 如果N0过高, 就采用较小的阈值σ1再重新得到一组新待选解数目N1。 重复此步骤, 直至阈值σn使得待选解数目Nn满足需求。 一般Nn处于200 ～500 之间较好,n的次数要小于3。

当得到距离搜索法的待选解后, 需要一个合适的选解策略。 原始的距离搜索法一般选择偏心率最小的一批待选解, 然后计算它们的平均值作为最终解输出。 为了能够详细地说明这种策略,本文假设了一个900km 高的太阳同步轨道观测平台, 该轨道高度基于2000 国家大地坐标系所采用的地球半长轴参数, 即6378.137km, 并使其观测两个仿真目标。 其中第一个目标的半长轴为7500km, 偏心率为0.001, 另外一个目标的半长轴为9000km, 其偏心率为0.1。 目标-1 的弧长设计为120s, 目标-2 的弧长设计为240s, 角度观测误差为2″, 只考虑J2长期项对轨道的影响。观测平台和两个目标的轨道根数见表1。

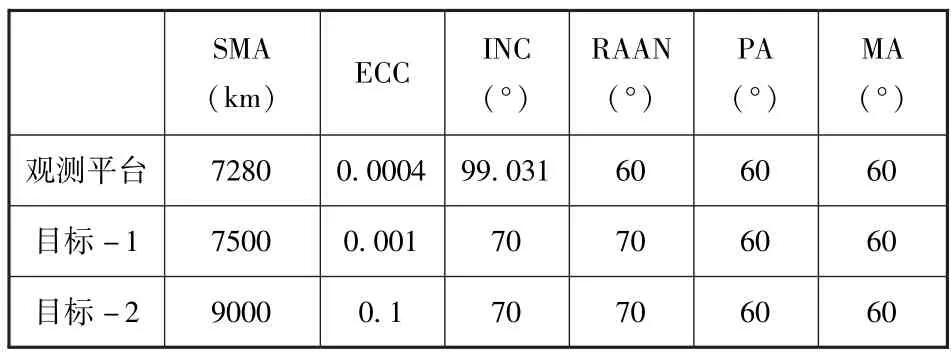
表1 天基观测平台和仿真目标的轨道根数Table 1 Orbital elements of the space-based observation platform and the simulation target

两个目标分别使用前述的阈值策略得到待选解, 这些待选解的“半长轴-偏心率” 分布见图1。 需要注意, 所有待选解的轨道根数都以弧段第一个观测历元为参考时刻。

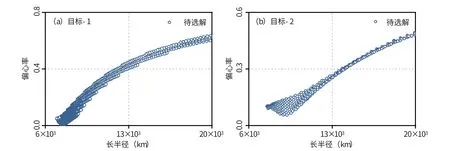
图1 距离搜索法下待选解的半长轴-偏心率分布图Fig.1 Semi-major axis-eccentricity distribution of the solution to be selected under the range search method

由图1 可见, 无论目标轨道是否为近圆轨道,待选解的半长轴-偏心率分布都呈现多条曲线平行或交错的形式。 显然, 基于半长轴-偏心率分布并不能有效地确定目标轨道的偏心率, 这会给最终解的确定带来影响。 而且, 这对于偏心轨道的影响更大一些。

不过, 分析待选轨道解的偏心率分布可以发现, 偏心率的频率分布并不是标准的高斯分布,可用概率密度函数f(e) 表示。 如果按照一定的偏心率间隔(ei,ej) 来计算待选解偏心率出现的频率直方图, 目标轨道的真实偏心率所对应的直方图频率是最高的, 其中i、j由算法设计的偏心率间隔数目确定。 此过程可用式(5) 表示:

式中,emax表示最高的直方图频率所对应的偏心率区间, 可用“max-间隔” 表述。

以前述两个目标的待选解偏心率分布直方图为例(见图2), 图中的偏心率间隔为0.05。

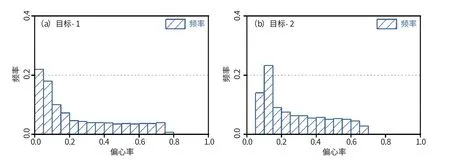
图2 距离搜索法下待选解偏心率的频率分布直方图Fig.2 The frequency distribution histogram of the deeccentricity to be selected under the range search method

在图2 (a) 中, 待选解偏心率处于0 ～0.05之间的频率为0.22, 处于0.05 ～0.1 之间的频率为0.18, 它们显著大于其他偏心率区间的直方图频率。 在图2 (b) 中, 待选解偏心率处于0.05 ～0.1之间的频率为0.14, 而0.1 ～0.15 之间的频率为0.23, 也显著大于其他偏心率区间的频率。 由此可见, 目标轨道的真偏心率就处于待选解偏心率最大频率所对应的偏心率间隔 (即max-间隔)。

在此基础上, 可对距离搜索法进行优化。 当max-间隔处于0 ～0.1 之间时, 表明目标轨道是近圆轨道, 此时可用小偏心率约束策略来选择最终的初轨解。 当max -间隔的最小值大于0.1 时,表明目标轨道是偏心轨道。 此时, 可以把满足max -间隔的前后两个间隔的待选解组合成一个新的待选解集合, 然后在这个集合中选择半长轴和偏心率的中位值作为最终初轨解的半长轴和偏心率。

用前述改正算法和原始距离搜索法对目标-1/目标-2 的测角弧段进行200 次初轨解算, 每次解算时的角度误差随机添加。 初轨最终解的半长轴和首尾斜距估计误差的均方根误差(Root-Mean-Square, RMS) 见表2。

表2 距离搜索法和改正算法的半长轴和首尾斜距估计RMSTable 2 Semi-major axis and fore-tail slant distance estimate RMS by range search method and correction algorithm

由表2 可知, 由于使用小偏心率约束策略,原始的距离搜索法解算目标-1 的轨道半长轴、首斜距、 尾斜距的估计误差分别为102.4km、117.3km、 127.1km, 要优于目标-2 的428.7km、344.0km、 270.7km。 利用优化算法, 两个目标的轨道半长轴/斜距的估计精度都得到了较大提升。改正算法对于目标-1 的轨道半长轴/首斜距/尾斜距的估计精度为49.4km、 62.7km、 72.9km,对于目标-2 的轨道半长轴/首斜距/尾斜距的估计精度为175.9km、 138.8km、 103.5km, 都高于原始距离搜索法的估计精度。 以上实验说明, 利用改进的距离搜索法, 可以为Gooding 法提供更加精确的斜距估计初值。

3 轨道偏心率判定方法

基于改进的距离搜索法所提供的斜距初值, 就可以基本确保Gooding 方法利用3 方向观测值解算初轨参数的收敛。 现假设观测时刻为ti(i =1,2,3) , 距离搜索法所提供的首尾时刻斜距值为ρ1、ρ3。 那么, 由式(2) 和Gooding-Lambert 方程, 可以得到目标位于中间ti时刻的一个解[4]。 若ρ1、ρ3为真值, 则与重合, 否则两者之间有偏差, 该偏差可用图3 表示[5-6]。

图3 目标函数示意图Fig.3 Objective function diagram

基于图3 中的几何关系, Gooding 方法用f和g表示偏差, 并作为首尾时刻斜距ρ1、ρ3的目标函数, 同时将ρ1、ρ3作为自变量, 并用x、y表示。 那么, Gooding 方法的函数关系可以表示为:

使用Newton-Raphson 迭代法, 自变量的迭代值应为:

式中,δx、δy为自变量的迭代值,fx、fy、gx、gy分别为目标函数f、g对自变量的x、y的偏导数, 可用数值微分方法得到。

经过式(6) -(7) 的反复迭代, 并结合Gooding-Lambert 方程, 即可得到一组由3 方向观测值得到的初轨解。 而对于一个具有数十甚至上百方向观测值的光学测轨弧段, 可以组成许多3 方向组合。

本文将一个光学弧段分为首部、 中部、 尾部三部分。 首部和尾部的弧段时长占总弧段时长的25%, 中部的弧段时长占50%。 每个3 方向组合的第一个方向来自首部, 第二个来自中部, 第三个来自尾部。 选择合适的方向组合, 保证Gooding方法所解算的待选解总数在200 ～500 之间, 和上节所讨论的距离搜索法的待选解数目一致。 同时, 将待选解数目在10 以下的弧段舍弃, 因为此时不能从待选解的分布中识别出有效的半长轴-偏心率分布特征。

与距离搜索法类似, 此处同样存在如何从待选解集中确定最终解的问题, 其中的关键是判定目标轨道的偏心率。 为此, 我们分析待选解半长轴-偏心率的二维分布特征。 设表1 所列的天基观测平台分别观测了表3 所列的6 个目标。 真轨道生成时只考虑了J2长期项摄动, 角度观测误差为2″, 观测频率为1Hz。 这些目标的Gooding 法待选解的半长轴-偏心率分布见图4 和图5。

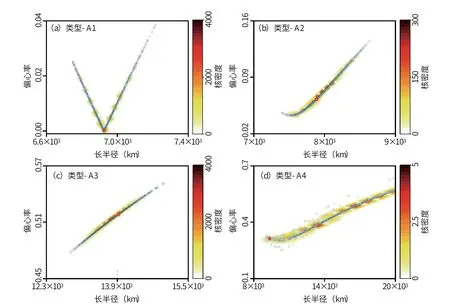
图4 类型A 的半长轴-偏心率分布图Fig.4 Semi-major axis-eccentricity distribution of type A

图5 类型B 和类型C 的半长轴-偏心率分布图Fig.5 Semi-major axis-eccentricity distribution for type B and type C

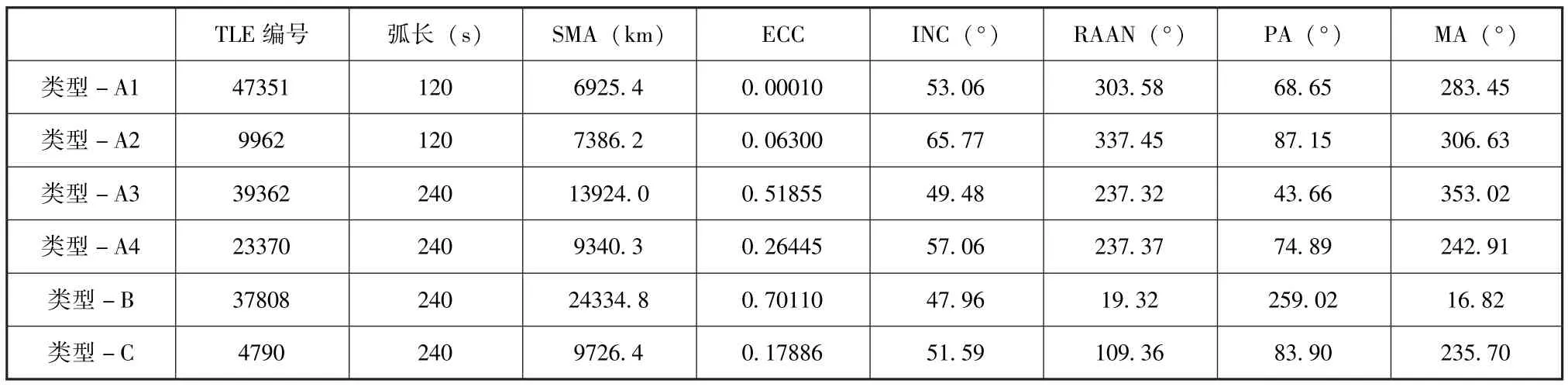
表3 TLE 目标的轨道根数Table 3 TLE Number of orbital elements of the target

图4 显示了Gooding 方法待选解最常见的半长轴-偏心率分布, 约占第三节实验弧段总数的92%。 与距离搜索法的多条半长轴-偏心率曲线不同, 尽管分布密度不均匀或线断裂, 但每个分布都呈现为光滑连续的折线或曲线。 对于这种类型的分布, 本文将其统称为类型-A, 从这种类型的待选解中, 来确定最终解相对比较简单, 而且确定最终解的准确性通常很高。

类型A 的半长轴-偏心率分布可以用一个或两个高次多项式方程进行拟合, 此时可假设待选解组合的偏心率为因变量ε, 半长轴为自变量α, 那么拟合方程为:

式中,ai(i =0,1,2) 为拟合多项式的系数。

在式(7) 基础上, 还需要判断拟合线段是否离散, 可用拟合优度指标R进行判定, 该指标的计算公式为:

其中,SSE表示残差平方和, 即

式中,εi表示待选解的真实偏心率值,ε︿i为由式(7) 计算得到的回归偏心率值。

其中,SSR表示回归平方和, 即

图4 (a) 为近圆轨道的分布。 它呈现为“V” 形, 底部的偏心率接近于0, 并且待选解的分布在底部附近密度最大。 这种V 型分布被称为类型-A1, 在偏心率接近于零的轨道上是最典型的分布。 其一般可以拟合出两条多项式方程, 且两个多项式都满足a2≈0,R ＞0.95 。 但随着偏心率的增加, 它逐渐演变成一条带弧度的曲线, 如图4 (b) 所示。 将偏心率最小的待选解作为类型-A1 的最终解, 将会获得较为准确的初轨参数估计值。 图4 (b) 中的分布被记为类型-A2, 可以用二次多项式近似, 即在由式(7) 所拟合的多项式中,≥0,R ＞0.95。 真解位于曲线曲率最大的位置。 当轨道偏心率大于0.15 时, 分布曲线呈现为类型- A3 或类型-A4, 分别如图4 (c)和4 (d) 所示。 其中, 类型-A3 最为常见, 其真解的半长轴和偏心率与待选解半长轴和偏心率的中位数接近。 其只能拟合出一条多项式方程,且满足a2≈0,R ＞0.95 。 但是, 如果是分布更为广泛的类型-A4 型, 则很难得出准确的最终解决方案。 类型-A4 的特征比较明显, 在4 个亚型中半长轴和偏心率分布范围最广。 此时, 虽然可以拟合出多项式, 但是R ＜0.8 , 真解通常位于待选解分布的底部附近, 但仍然很难确定准确的最终解。 幸运的是, 类型-A4 仅占所有分布的4%左右。

图5 (a) 显示了半长轴-偏心率分布的另一种常见形状, 称为类型- B, 约占所有分布的6%。 在这种类型中, 待选解聚集在一个封闭的区域内。 这种类型的真解通常非常靠近区域的质心, 因此我们使用质心来确定最终解。

其余的半长轴-偏心率分布不太规则, 难以描述, 约占总数的2%。 这种类型称为类型-C,如图5 (b) 所示。 造成类型-C 半长轴-偏心分布的主要原因是距离搜索法的斜距初值估计不准确, 导致Gooding 方法收敛错误。 在这种情况下,没有办法确定最终解, 一般判定初轨解算失败。

需要注意的是类型-B 和类型-C 的拟合优度指标R都较低, 需要加入专家判断来辅助分类, 机器学习算法也可以提供一个初步的分类参考[11]。

综上所述, 本方法通过从候选解集找到半长轴-偏心率分布中最密集的点来确定最终解。 因此, 如果半长轴-偏心率的分布范围很广, 则很难确定准确的最终解。

基于以上讨论, 图6 为根据半长轴-偏心率分布判定目标轨道偏心率的算法流程。

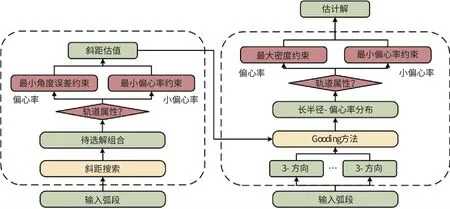
图6 算法流程图Fig.6 Algorithm flow chart

4 实验结果

本文设计天基仿真实验来评估上述最终解优选策略的有效性。 考虑到不同轨道高度目标与观测平台的相对速度的不同, 观测场景和几何特征大不相同, 因此本文区分了不同种类的轨道目标。 它们的轨道参数可见表4。

表4 不同轨道类型的轨道参数Table 4 Orbital parameters of different orbits

天基观测平台轨道信息见表1, 设计为900km 高的太阳同步轨道, 该轨道高度基于2000国家大地坐标系所采用的地球半长轴参数, 即6378.137km。 仿真目标的初始轨道信息来自于2023年6月1日-2023年6月3日的TLE 数据库, 并转化为TLE 根数对应时刻下的开普勒根数。 同时, 设计LEO1和LEO2的弧段长度为120s, MEO、 HEO 和GEO 目标的弧段长度为240s。 每个目标的轨道考虑J2的长期项影响,目标角度误差为2″, 观测频率为1Hz。 最后捕捉到了9325 个目标, 假设每个目标只观测到一个光学弧段。

将原始的Gooding 方法通过多组待选解求平均的策略, 记为算法-1。 同时, 将基于Gooding方法, 并使用优选策略进行轨道偏心率判定方法, 记为算法-2。 这两种算法都使用改正的距离搜索法所提供的斜距初值进行初轨解算。 分别将两种算法应用于各类型下的光学弧段初轨解算。需要注意的是, 由于优选算法只是针对于待选解进行优化的算法, 因此其收敛率与原始Gooding方法是相同的。 在本次实验中都为94.7%, 即8834 弧段成功收敛。 两个算法的半长轴与倾角误差RMS 见表5。

表5 两种算法的半长轴和倾角误差RMSTable 5 The semi-major axis and inclination error RMS of the two algorithms

从表5 中可以看出, 相比于算法-1 而言,算法-2 半长轴、 轨道倾角的估计精度更加精确。而且相比于偏心轨道而言, 算法-2 在小偏心率轨道上的初轨估计精度的提高更显著。 算法-2在LEO1、 MEO、 GEO 轨道上的半长轴估计精度为55.93km、 46.64km、 150.16km, 而算法-1 只有162.10km、 357.95km、 2153.03km, 说明新算法能够通过待选解的半长轴-偏心率分布, 准确地区分出目标的轨道属性, 并给出较准确的轨道估值。 算法-2 在LEO2、 HEO 轨道上的半长轴估计精度为86.90km、 419.47km, 相比于算法-1的120.16km、 467.53km, 也有较大提升, 也说明了新算法在偏心轨道上的作用。 图7 为两种算法在前述不同轨道类型下的半长轴、 轨道倾角的误差分布箱线图。

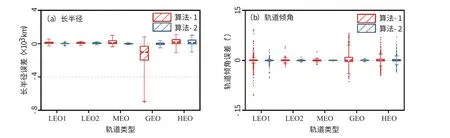
图7 天基仿真情景下Gooding 法和I-Gooding 法的误差箱线图Fig.7 Errorbox plots of Gooding method and I-Gooding method under the background of space-based simulation

从图7 (a) 中可以看出, 相比于算法-1 的半长轴误差分布而言, 算法-2 在小偏心率目标上误差分布更加集中。 这是由于新算法能够根据Gooding 算法待选解轨道半长轴-偏心率分布, 准确地识别小偏心率轨道, 并据此给出精确解。 同时也可以看出, 算法-2 在偏心轨道上的误差分布相比于算法-1 更集中。 从图7 (b) 可以看出, 算法-2 的轨道倾角误差分布相比于算法-1更靠近0, 说明新算法在轨道倾角的估计中也能获得较高的精度。

以上实验结果说明, 根据Gooding 法待选解的半长轴-偏心率分布, 本方法可准确识别目标轨道的偏心率, 并得到较精确的初轨。 这给今后的光学观测初轨确定工作提供了新的思路。

5 结论

随着光学观测技术的发展, 一个数十秒至数分钟长的短弧一般有数十甚至上百个观测方向。为使经典的Gooding 初轨确定方法能够有效地处理光学多向观测弧段, 本文主要从以下两个方面对现有算法进行了改进。 首先, 对于只能应用于小偏心率初轨计算的距离搜索法, 按照其待选轨道解的偏心率分布特征, 准确识别出目标轨道的偏心率, 从而使距离搜索法应用于偏心轨道时也可得到较为精确的初轨参数与斜距。 其次, 根据Gooding 法的3 方向待选解半长轴-偏心率分布,能够准确识别目标轨道的偏心率, 并能够根据这些特征选择合适的初轨解。

利用天基仿真光学观测数据的实验验证了改进距离搜索法和优选算法的有效性。 实验结果表明, 对于不同轨道类型的光学短弧初轨确定, 所提出的轨道偏心率判定方法均可提升初轨估计结果的精度。 新算法在近圆轨道初轨解算中表现优异, 对于LEO1、 MEO、 GEO 短弧初轨确定, 半长轴误差的 RMS 值为 55.93km、 46.64km、150.16km, 倾角误差的RMS 为0.18°、 0.05°、0.14°。 对于偏心轨道LEO2、 HEO, 应用新算法的半长轴误差RMS 为86.90km、 419.47km, 倾角误差RMS 为0.16°、 0.90°。

因此, 相信本文所提出的空间目标光学短弧轨道偏心率判定方法有助于光学空间监视中的新目标识别和关联编目, 从而为自主编目能力提升做出贡献。