空间目标编目定轨理论与技术进展
杨磊, 路毅, 刘磊
(1. 西安电子科技大学, 西安 710126; 2. 中材节能股份有限公司, 天津 300400)
1 引言
近年来, 随着空间碎片对航天活动的威胁日益增大, 为了有效评估空间碎片与在轨卫星碰撞风险, 当前对空间目标编目的需求愈加迫切。 空间非合作目标的轨道确定是空间目标编目领域的关键技术之一, 无论目标观测、 数据关联或编目管理, 都以准确的轨道确定和外推预报作为前提条件。 本文通过调研近年来国内外关于空间目标轨道确定的相关文献, 总结归纳了空间目标定轨领域技术体系中的新进展, 重点研究了初轨确定、 精密定轨和联合定轨的新进展。 同时, 分析了新进展、 新方法的优势特点及应用的局限。
对于已经编目的目标, 受到各种摄动的影响, 编目目标轨道根数不断演化, 因而编目信息具有一定有时效性要求, 需要不断对其观测并更新轨道。 空间目标编目库维护流程如图1 所示,根据目标运动状态的初始信息计算出目标在未来段时间内的轨迹, 将其与观测轨道数据进行比较, 确定能否关联成功, 绝大多数目标在这一轮都能关联成功。
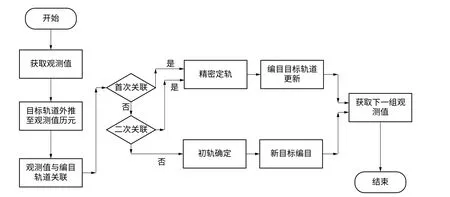
图1 空间目标编目库维护流程图Fig.1 Spatial object inventory maintenance flow chart
当出现多个目标轨道相近或者极少目标存在机动的情况下, 很有可能关联不成功, 需要通过追加更密的观测值、 修改定轨残差阈值等进行“二次关联” 判断。 目前普遍将利用少量数据计算轨道的算法称为初轨确定算法, 将根据后续数据提高定轨精度的方法称为跟踪算法或精密定轨算法, 对于观测站网, 还存在多观测源的联合定轨问题。 本文从初轨确定、 精密定轨和联合定轨三个方面研究空间目标定轨技术中模型和算法的研究现状和进展。
2 空间目标的初轨确定技术
初轨确定是利用短弧段的观测数据, 采用简单、 快速、 简化模型的动力学定轨方法估计初始轨道。
2.1 传统测角定轨方法
空间目标的初轨确定一般基于非线性二体模型, 由简单的迭代计算完成, 为了获得空间目标在某一时刻的矢量位置和速度, 必须同时知道两个时刻的测距和测角或三个时刻的测角。 然而,测距要求有特定的星载设备来确定信号往返时间, 即通常为合作目标。 非合作目标的测量通常以测角为主, 因此测角法定初轨在编目技术是主要方法。 测角定初轨方法很多, 根据其算法根源, 可以归纳为两类: Laplace 法和Gauss 法。
Laplace 法以光学测量资料为背景, 利用三个时刻的测角数据确定某历元时刻的位置矢量和速度矢量。 需要利用多项式拟合测角数据得到角度的一阶变化和二阶变化, 利用Cramer 法则计算目标和光学传感器的距离。 后续发展出适用于多个测角数据的约束域算法[1-5]。 这个算法需要拟合测角数据得到角度的一阶变化, 用角度、 角度变化、 距离、 距离变化表示目标状态, 用能量构造约束[6-8]。 多项式拟合得到的角度变化相当于两个额外的测量参数, 求解距离和距离变化两个变量从而计算目标轨道。
Gauss 法依然属于三点测角定轨法。 用拉格朗日系数关于时间间隔级数的前两项带入定轨方程, 得到关于单变量的多次方程。 根据定轨结果重新计算拉格朗日系数构造迭代过程进一步提高定轨精度。 针对多个测角数据, Karimi 扩展了定轨方程用多个时刻的距离做变量计算目标轨道[9]。 两个时刻距离即可确定唯一的目标轨道。利用多个时刻的距离作为变量时, 在更新拉格朗日系数迭代时只选取其中一部分。 但这可能造成一定的系统误差。
2.2 改进的Laplace 法定初轨
为了满足测量几何关系式, Laplace 法要求三个时刻观测的单位方向矢量不能共面或在一个平面附近而且相隔时间较短。 为了便于使用, 国内外结合具体应用对两种方法进行了一定程度的改进, 即改进的Laplace 法和改进的Gauss 法。 相对而言, Laplace 方法比Gauss 法形式更为简洁, 用于初轨确定更为有效[10]。
改进的Laplace 方法是在二体问题意义下严格的, 未作任何近似处理, 其最大特点在于消去了条件方程中的相对距离, 可以综合处理多次光学观测数据, 程序比较简单。 但是, 由于其初值的选取是基于最简单的圆轨道假设, 收敛精度不高; 而且其中f、 g 级数的计算也是基于二体无摄的假设前提下计算的, 因此本身的定轨精度也并不理想[11]。 由于仅测角观测下Laplace 方法初定轨存在上述的问题, 并且在迭代计算中需要设定合理初值, 初值选择不当很容易造成迭代不收敛或收敛至平凡解[12], 因此关于选择合理初值或改善初值条件开展的研究工作也较多[13,14]。 Sokolskaya M J 对测量数据的拟合残差进行多次拟合迭代, 改进了Laplace 法, 提高测角的一二阶导数的精度[15]。 李艳斌则在改进的Laplace 法迭代过程中增加调整f、 g 级数的惯性项, 从而达到较高的收敛速度, 改善了收敛性[16]。
在对Laplace 法的各种改进中, 需要特别指出的是一种很具代表性且在国内的长期定轨实践中行之有效的方法单位矢量法[17-19]。 单位矢量法是一种可用于初定轨和轨道改进的非线性定轨方法, 通过定义一系列单位矢量简化条件方程,既可避免状态向量对轨道根数的偏导数, 又可分离不同类型的数据, 便于不同数据的加权处理。单位矢量法相对于改进的Laplace 方法而言, 其本质的改进是改变了条件方程的形式, 能综合利用各种测量信息如角度、 斜距和斜距变化率等,并采用最小二乘方法加权处理, 迭代求解。 经过理论研究和实践应用证明, 单位矢量法基本解决了初轨计算中轨道半长轴不易定准的困难, 确实有利于提高初轨测定精度, 并可以改善整个计算过程的收敛性。
2.3 新的测角初定轨方法
当前, 初轨确定已不再局限于简单的三次测角数据定轨, 而是尽量利用多观测站多种类型观测数据进行定轨, 并充分利用测量数据统计特性提高初轨精度, 出现了一些新的测角初定轨方法。 广泛应用的Gooding 算法[20-21]、 刘光明的同伦延拓法[22]这些可以看作一种微分改进。 Karimietal. 还提出一种了仅测角定轨问题解决思路[25,26]。 王志胜等提出了图解法, 并用遗传算法进行相关解算[27]。 Vitarius P J 等从开普勒运动定律推导出确定目标斜距的方法, 无需知道万有引力常数、 中心体质量和时标, 采用五个数据一组定轨, 不过, 该方法对测量噪声非常敏感[28]。Milani A 等研究了一种新的轨道参数表示法, 利用一些很短弧段的角度及其导数进行定轨, 如果使用经典的定轨方法则无法利用这些短弧段进行定轨, 其研究表明如果仅用两个短弧段进行定轨最为困难[29]。 Virtanen J 针对极短弧、 观测几何较差时的初定轨不易求解问题, 提出了一种利用Bayes 估计理论的初定轨方法, 该方法通过对两个或多个测量数据加入随机偏差, 并产生随机的地平测距, 以此重复计算得到了符合测量数据的候选轨道, 并以此估计出空间目标轨道根数的概率密度函数, 可以在一定程度上解决具有先验观测的极差测轨目标的丢失重捕和初定轨等问题[30]。
3 空间目标的精密定轨技术
由于初始轨道根数和摄动运动方程中动力学模型的不准确, 需要利用足够的观测资料来改进动力学模型中不精确的参数, 使得轨道参数精确, 该过程过去称为轨道改进, 现在也称为精密轨道确定或精密定轨。
精密定轨将一个动力学问题转化为常微边值问题, 由常微初值问题的求解过程与转化为边值问题后求解线性代数方程的过程相结合, 形成一个多变元迭代计算, 其实质是通过求解轨道动力学微分方程组而对初始轨道不断改进。 因此, 定轨的精度与速度不但依赖于观测资料的精度和微分方程组的具体求解算法, 同样依赖于初始轨道的精度与准确性, 经大量观测资料改进后的初轨就是一定意义下的精轨。 在初轨确定的基础上,可用长弧段测量获取的大量测轨数据进行空间目标的轨道修正和确定, 有基于微分修正方法、 拓展卡尔曼滤波算法、 粒子滤波算法等。 最具代表的算法就是数据批处理的最小二乘法和卡尔曼滤波进行的序贯处理相关算法。
3.1 事后精密定轨技术
事后精密定轨一般采用数据批处理的最小二乘估计(Least Square, LS)[31-34], 最小二乘法是一种基于观测数据与模型数据之间的差的平方和最小来评估模型参数的方法, 最早是由Gauss 为解决天体运动轨道的预报而提出的, 是状态估计和参数估计理论的基础。 LS 法的数学模型和计算方法简单, 对于严格正态分布数据具有一致最优无偏且方差最小特性, 广泛应用于航天器精密轨道确定等研究领域[75]。 它通过泰勒级数展开将非线性函数进行线性化, 从而将非线性最小二乘问题转换成线性最小二乘问题求解。 但是, 当参数初始值与平差值相差较大时, 线性化过程的模型误差将可能导致错误的平差结果。 非线性最小二乘法是在此基础上发展而来的, 它避开了精确计算参数初始值的难题, 以及线性化过程中的模型误差。 常见的非线性最小二乘法有Gauss-Newton方法和Levenberg-Marquardt 方法[35-37]。
3.2 实时精密定轨技术
序贯法在空间目标轨道确定中应用, 需要提供有效的轨道先验信息, 确定和计算先验状态误差协方差矩阵, 输出包括状态估计和状态协方差矩阵, 序贯法轨道确定方法的总体思路是通过状态估计的时间更新和观测数据更新实现迭代递推。 状态估计误差在更新间隙随时间增大, 在测量数据更新时减小, 所以常用于于实时精密定轨中。 Kalman 和Bucy 为解决线性最小方差估计公式难以实际应用计算的问题, 提出最优线性滤波递推算法, 即卡尔曼滤波[38-39]; 与最小二乘批处理方法相比, 卡尔曼滤波对观测数据进行序贯处理, 无需存储数据或仅需存储一次观测数据,可应用于实时或准实时的空间目标跟踪定轨。 通过应用验证发现, 经典卡尔曼滤波算法常出现有偏估计和发散现象, 因此, 各类改进算法应运而生。
目前主要的算法包括扩展卡尔曼滤波算法(Extended Kalman Filter, EKF) 和无迹卡尔曼滤波算法(Unscented Kalman Filter, UKF)。 EKF 通过一阶Taylor 级数展开将非线性问题用线性方法近似处理, 当系统非线性较弱且噪声特性符合高斯假设近似成立时, 通常可以获得较好的估计性能[40]。 但是对于仅测角跟踪定轨, 由于没有空间目标的距离测量信息, 其可观测性较弱且系统模型较为复杂, EKF 的一阶线性化截断误差会带来不稳定性, 容易导致滤波性能恶化。 Aidala 提出适用于仅测角跟踪的伪线性滤波(Pseudo Linear Filtering, PLF) 跟踪算法, 避免了病态协方差阵的产生, 该算法稳定性较EKF 方法好[41,42]。 之后, 学者们通过不断改进, 提出了修正增益的EKF 算法(Modified Gain EKF, MGEKF)[43]、 旋转协方差矩阵的EKF 跟踪滤波(Rotated Covariance EKF, RVEKF)[44]和修正协方差的EKF 跟踪滤波(Modified Covariance EKF, MVEKF)[45], 改善了滤波器的性能。 除上述函数近似法外, 采样近似法是对最优非线性滤波器逼近的另一类方法。 采样近似法所近似的对象是系统状态量的条件概率密度函数, 主要有无迹卡尔曼滤波(Unscented KF, UKF)。 UKF 通过选择有限确定样本点来逼近系统状态的条件概率密度函数, 所选择样本点可以完全捕获到状态量的均值和协方差,在高斯噪声假设下适用于任何非线性系统[46,47]。样本点通过非线性函数传递后, 其非线性分布统计量的计算精度至少可以达到二阶Taylor 展开的估计精度, UKF 是UT 变换和卡尔曼滤波算法的结合, 可有效克服EKF 的估计精度的和稳定性差的缺陷。 由于EKF 是一阶滤波, 而UKF 考虑了泰勒展开中的二次项, 属于二次滤波算法, 虽然能够有效减少由于线性化带来的估计误差, 但计算量大大增加。
在各类应用中, 卡尔曼滤波算法结合实际情况有各种改进, 比如有基于小波变换的卡尔曼滤波外推算法、 基于自适应采样平方根的无迹卡尔曼滤波算法、 双无迹卡尔曼滤波算法等[48-51]。这些改进型卡尔曼滤波算法适用的场景和条件各不相同, 一种完美、 通用的卡尔曼滤波算法是不存在的, 大部分卡尔曼滤波算法都是以原有研究为基础, 对参数估计、 误差计算等方法改进和修正而来。
4 空间目标的联合定轨技术
联合定轨按照实现方法不同可以分为: 多种观测源的联合定轨、 定轨模型的联合定轨、 以及多数据融合的联合定轨。 多种观测源的联合定轨和定轨模型的联合定轨这两者都是从数据源或模型的特征层面进行联合, 从而在定轨过程中消除或减小某一类误差源的影响。 多数据融合的联合定轨是信息层的一种融合处理, 降低不确定性,从而获得更为可靠的定轨结果。
4.1 多种观测源的联合定轨技术
基于多种观测源的联合定轨的主要目的将多个观测源进行优化配置和性能互补, 从而获得满意的定轨结果, 特别是利用光学传感器与雷达的联合定轨精度最高。 空间目标的观测目前分为地基与天基两种方式, 与天基观测方式相比, 地基观测方式的优点在于可以提供较大的发射功率与观测孔径等参数, 可以有效的增大观测能力。 因此, 目前对空间目标的跟踪与编目主要依托地基观测方式。 地基空间目标观测系统设备庞大、 配置复杂, 易受大气环境和地球曲率的影响, 并且其可观测性、 可跟踪区域以及几何特征感知等方面都存在难以克服的局限性。 天基空间目标观测不受地球曲率和国家地域的局限, 也不易受到复杂大气环境的影响, 但单次测量任务内对目标可能仅获得数十秒至数十分钟弧段的观测数据, 而短弧测量所能反映的目标运动特性或轨道特征有限, 特别是对于新发现目标, 在单个较短观测弧段内较难有效定轨, 需与地基系统互为补充, 提升定轨性能。
地基观测方式主要采取被动式地基空间望远镜和主动式地基雷达。 地基空间望远镜优点在于具有相对较大的视场, 可以在较大的范围内搜索目标, 同时也可以探测很远距离的目标。 但缺点是有光照要求, 可观测时间短, 观测条件要求较高, 无法做到全天候全天时的观测, 同时也只能得到角度光度信息而无法获取距离值。 地基雷达虽然可以做到全天候全天时, 但由于其地理位置的局限, 其只能观测其位置上方一定天区的范围, 且其系统庞大复杂。 因此, 主动探测技术与被动探测的融合, 能更好的结合利用两种探测手段的各自优势, 实现观测方式上和数据处理上的互补和增强, 并且一次性获得目标定轨所需的轨道参数。
4.2 基于模型的联合定轨技术
基于模型的联合定轨主要指联合利用空间目标的动力学信息和运动学信息以抑制或补偿单一类型状态模型误差的定轨方法, 这种思想在简化动力学中得以表现。 王正明研究了空间目标摄动误差的节省参数建模[52], 赵德勇研究了多模型的最优融合加权处理和用户星、 观测站的联合定轨模型[53]等, 都也是基于模型联合定轨的一种应用。 可以看出, 基于模型的联合定轨的目的在于消除或减小模型误差的影响, 从而在定轨过程中消除或减小某一类误差源的影响。 朱珺采用模型联合方式, 将批处理和序贯处理相结合对目标轨道进行改进。 此方法能有效提高计算效率, 提升参数估计的精度, 算法的稳定性较好[54]。
4.3 多源数据融合的联合定轨
利用观测数据消除误差源影响的联合定轨是指通过冗余测量数据抑制单一数据系统偏差的处理方法, 其主要降低不确定性, 以提高观测数据的精度和可信度, 是联合定轨体制中最基本的联合形式。 其最典型的例子就是利用多设备测角数据进行融合, 标校和修正测量系统误差, 能保证测量精度。 刘也、 朱炬波等人采用测量数据的多项式拟合方式, 进行轨道平滑, 利用求导匹配特性, 增强数据的冗余度, 为提高数据处理和空间目标轨道计算精度提供了思路[55], 目前该方法在实际轨道数据处理中为常用方法。 淡鹏、 李恒年等人探讨了直接使用非完备数据, 采用变维矩阵运算, 融合多观测数据, 减低单设备误差对定轨精度的影响[56]。 而另一种应用是消除测站误差的影响, 消除天基观测平台的星历误差影响, 例如可以将地面测控网对天基观测平台、 天基观测平台对空间目标的观测数据统一处理, 以得到天基观测平台和空间目标的最优状态估计。
5 结论与展望
随着测量设备性能、 计算机处理速度、 人工智能等日新月异的发展, 空间目标轨道确定领域的研究也正蓬勃发展。 改善空间目标的定轨精度, 完善轨道动力学模型和提高测控设备的观测精度一直是当前国际上空间目标精密轨道确定领域的研究热点, 国内外在空间目标轨道确定方面取得了丰硕的成果。 总的来说, 空间目标的初轨确定相对简单, 比较成熟, 相关研究主要集中于误差修正、 定轨算法改进等方面。 相对来说, 空间目标的精轨计算受各种外力作用产生轨道偏差需要积累大量测量数据, 无法实现强时效性的轨道确定, 但一些新的滤波算法可以在空间目标轨道确定中的到应用, 需要进一步在实践中考察其效果。

