聚焦度量 发展量感

黄金娥

量感主要指对事物的可测量属性及大小关系的直观感知，是小学数学核心素养的主要表现。教学中，教师如何引导学生迁移、运用已有的度量经验来把握面积与周长的区别和联系，使学生对“面积”的理解从直观感知走向度量认知，进而形成良好的量感呢？

一、分析面积的度量意义

面积是度量几何中最基本的概念之一。面积的测量就是确定度量对象、选用度量单位和赋予度量值的过程。从字面上，“面积”中的“积”指度量方式，有累积、乘积的意思。其中“累积”有两层含义：一是积小面成大面后，数出一个数值表示其大小；二是积线成面。所以说，“面的大小”并不是指“哪个面大、哪个面小”或指向“相差”，而是指“每个面的实际量值”。测量就是数一数、量一量有多少个这样的计量单位。

《小学数学教材中的大道理》一书指出，早在婴儿阶段，人就已经能够辨别两块饼的大小。教学时，教师不能仅从“面的大小”层面来分析面积的定义，还要从度量的视角引导学生真正理解面积的意义。基于此，教师可以结合给教室铺地砖的生活情境，先引导学生理解铺砖的过程其实是把一块砖看作一个计量单位，正好铺满教室地面的砖的块数就是我们度量出的教室面积的大小，再引导学生从实物过渡到图形，进一步体会面积的意义。

二、体会面积度量标准要统一

面积单位即度量面积的标准。面积单位不仅仅只有边长1厘米、1分米、1米的正方形，它们只是一些标准的面积单位。在比较面积的大小时，统一度量单位十分重要。

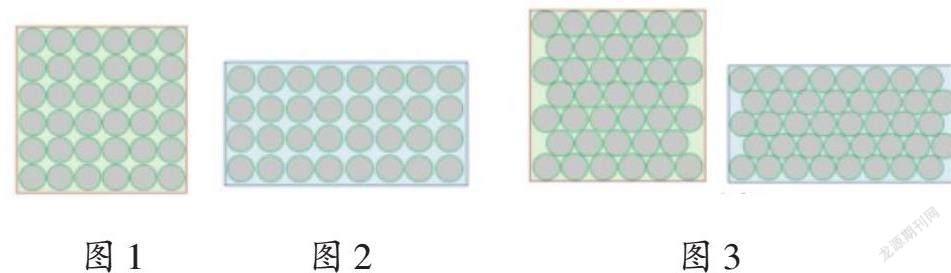
笔者对比人教版、北师大版、苏教版和浙教版数学教材“面积”相关内容后发现：北师大版和浙教版直接给出借助拼摆小正方形得出面积的方法；苏教版用同一张纸去量不同图形的面积，体现了度量面积要用同一个标准；人教版呈现了“选用哪种图形作单位来测量面积”的探索活动。在人教版数学教材的探索活动中，学生选用三角形、圆形作单位来度量长方形的面积也能得出正确结果，他们能体会到选用正方形作为面积单位的合理性吗？例如，图1的正方形中摆了36个圆片，图2的长方形中摆了32个圆片，学生根据圆片数量可以得出正方形的面积比长方形面积大的结论；但如果采用图3的摆法，正方形中摆了39个圆片，长方形中摆了40个圆片，就会造成长方形面积反而比正方形面积大的错觉。

如果教师在课堂上引入上述对比操作和辨析的过程，学生一定会发现其中的奥秘，对面积的概念和选择合适的面积度量标准产生更加深刻的体会。

在比较两个图形（长5厘米、宽3厘米的长方形和边长4厘米的正方形）面积大小的环节，除了准备20个边长1厘米的小正方形，笔者还准备了10个边长2厘米的小正方形，让学生度量图形面积时有不同的选择。实践中，学生呈现了以下几种摆法：①长方形和正方形都用边长1厘米的小正方形度量；②用边长1厘米的小正方形度量长方形的面积，用边长2厘米的小正方形度量正方形的面积；③如下图，用边长2厘米的小正方形度量面积，不够量的部分摆满边长1厘米的小正方形。

摆法1选择统一的标准来量，方便比较；摆法2虽然把各自要度量的面摆满了，但是标准不一样，不能直接比较；摆法3本质上仍然是用边长1厘米的小正方形作为标准来测量。笔者引导学生用两种大小不一样的正方形作为度量面积的工具，使学生体会到比较面积时统一度量标准很有必要。

三、感悟面积度量的本质

为深化学生对面积度量本质的理解，笔者没有采取常规的通过测量、填表、观察等活动推導出长方形和正方形面积公式的教学流程，而是引导学生借助“画一画、剪一剪、摆一摆”等活动，探讨长方形面积与它的长和宽之间的联系。

课堂上，笔者设计了以下两个问题，引导学生通过动手操作来感知：①一张长10厘米、宽8厘米的长方形彩纸，最多可以剪出多少个面积是4平方厘米的小正方形？②一张长10厘米、宽8厘米的长方形彩纸，最多可以剪出多少个边长4厘米的小正方形？这两个问题看似是同一类问题，其实不然。实践中，学生往往把这两个问题都理解成“大面积里包含多少个小面积”，直接列算式计算得出“10×8÷4=20（个）”“（10×8）÷（4×4）=5（个）”。部分学生不能理解为什么这样解答问题①是对的，这样解答问题②却是错的。问题②的解法错在哪里呢？笔者引导学生通过画一画、剪一剪直观地看到：问题①是以4平方厘米为面积单位（边长2厘米的正方形），问题②是以16平方厘米为面积单位（边长4厘米的正方形）；长方形的长和宽正好是2厘米的整数倍，但并不是4厘米的整数倍，在大长方形中剪下4个边长4厘米的小正方形后，剩余的长8厘米、宽2厘米的小长方形的面积虽然也是16平方厘米，但不是题目中需要的正方形。有了这样的直观操作，学生对图形面积大小的实质有了更深入的理解。

以上学习活动，让学生明确了长方形的长和宽包含多少个面积单位与面积单位的大小有关：当长和宽以厘米为长度单位时，适合选用边长1厘米的小正方形去量；长和宽分别是几厘米，就包含几个边长1厘米的小正方形。在此基础上，笔者引导学生讨论长方形的面积等于“长×宽”的原因，搞清楚为什么两个长度相乘就能得到面积。学生通过摆的直观操作发现：“长×宽”即“一行摆的个数×摆的行数”，乘积是度量单位的个数；实际上，长方形的面积应该在长乘宽的基础上乘“1”（“1”指度量单位的面积，也就是1个小正方形的面积是1平方厘米），而乘“1”可以省略。

四、厘清度量过程中的运动不变性

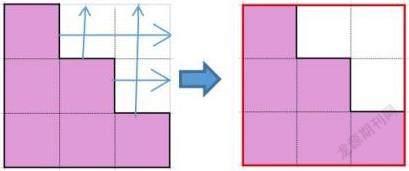
测量的过程隐含了运动不变性。如下图，测量不规则图形的周长时，把边做相应的移动，其长度并未改变，可以将不规则图形转变成正方形来求周长。

面积也存在运动不变性。如下图，移动不规则图形右下角的一个面，正好可以将该图形补成一个正方形，很容易得出其面积。如果计算面积时移动了边，面积显然会变大。

教学时，笔者出示上述两个问题，引导学生分析周长和面积的运动不变性，为后续学生推导平行四边形面积公式、三角形面积公式等奠定基础。

度量源自数量大小比较的需要。通俗地讲，长度度量的本质是以短量长，面积度量的本质是以小片量大片，体积度量的本质是以小坨量大坨，角度度量的本质是以小角量大角，度量的本质即“以小量大”。从“为什么要度量”“统一度量单位的必要性”“度量工具的选择”和“度量的本质”等方面展开教学，有助于发展学生的量感，让学生养成用定量的方法解决问题的思维习惯。

（作者单位：宜都市实验小学）

责任编辑 刘佳