数式结构贯代数
王琳琳


摘 要:代数问题占据了初中数学的半壁江山.但是代数问题往往结构多样,形式多变,学生在处理问题时常常遇到困难.为了帮助学生更好地解决代数问题,教师在教学过程中要抓住数式结构这个关键,引导学生以此为解题的落脚点与突破点.
关键词:代数;数式结构;解题教学
《义务教育数学课程标准(2022版)》增加了两个代数基本事实,增加代数推理.将“数与代数”领域整合为“数与运算”“数量关系”两个主题.史宁中教授认为数学基本思想无外乎抽象、推理、和模型思想.代数领域的抽象主要体现在用符号表示数、数量关系和变化规律.而推理建立在概念符号的基础上,与几何中的推理相比,代数中的推理则偏重计算,通过计算和推理比较数式,数量关系.“数量关系”通过式子表达,研究数式结构对于代数教学大有裨益,本文将结合专家讲座浅谈初中教学中如何充分利用数式结构指导代数教学.
1 教学观点
在生长数学公益讲坛中,诸士金老师指出从小学到初中数学学习的两大困境:
“数系扩充和用字母表示数”
以此抛出第一个具体问题1:“3x+1怎么看”?
观点1:从宏观角度说,从数到式的结构化认识是对现实中数、数量以及数量关系的抽象.
观点2:从动态和静态观点看,3x+1流动起来看是函数,是规律,3×1+1,3×2+1、…静态结构可以看成AB结构+1可以看成A+B结构.
观点3:套入不同的问题背景对应不同的问题,不同的角色,买东西,x是苹果的个数,1是塑料袋的价格;出租车起步价1元,超过里程每公里3元……
观点4:数量关系在数学的大家庭里能反映出位置关系,即数形结合.
观点5:式结构除了可以看成代数式结构还有算式的结构如A+B,A=a×b一结构是一级运算,二结构是二级运算.
诸老师补充:数量及数量关系的抽象需要更多问题巨象化说明并紧接着抛出问题2:
“2x+3y=5怎么看?方程的式结构你怎么看”?
观点1:A+B=5,A和B互为控制关系,x是y的函数,y也是x的函数,但若变为A2+B2=5,则A与B只互为控制关系,而非函数关系.
观点3:式结构可以看成f(a):从a开始,追求通透的数学理解,使其结构脉络分明,不仅要知道结构的结点,也要关注建立不同式结构之间的关系、法则和思想方法,这是f.
诸老师总结:研究数的结构化特征是基于数感、符号感基础上的抽象意识、推理意识(运算),而进入初中之后研究式的结构化特征是基于数结构特征的一般化研究,能更为系统全面地刻画现实世界中的数量、数量关系及其变化的规律性,有利于发展学生的抽象能力,凸显式结构的一般性特征.关注式结构的内在特征及其结构的演变,可以更好地在数学内部发展推理能力、运算能力,凸显式结构发展性特征.
特级教师卜以楼接着作阶段性总结:
从1开始,从1到a,一切从a开始,1是数字,a是字母,y=ax2,y=a(x+1)2…给数学以生命,它会给你无限精彩,把数学上成生命成长的课,那么学生不再是学数学,而是享受数学……
那么“式结构的教学怎么进行?”几位老师以具体案例给出了答案.
案例1:以“字母表示数”为例
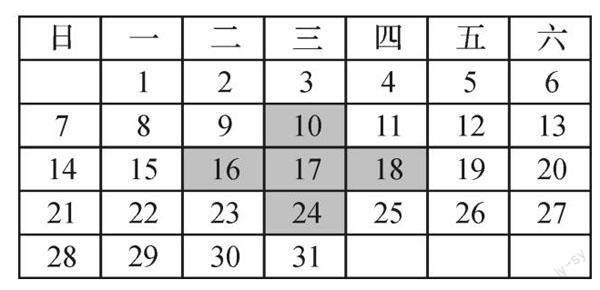
【例题】 (1) 框图中五个数的和与中间的数有什么关系?这个结论有一般性吗?
(2)图中有这种位置关系的5个数的和是95,求这五个数.
(3) 在日历表中你还能发现哪些规律?
(4) 你还能提出哪些问题?
这里可能提出下列问题:
问题1:在生活中,图表可以表示什么?
问题2:在数学中,有用符号表示的例子么?举例说明
问题3:你能将这些符号表述的例子分类么?
问题4:你怎么看待用字母表示数中的字母?
这里图表其实对应的是数,第一次接触的话,要让学生体会用字母表示数的必要性,有一部分用字母表示数的意识和观念,要提升为能力,首先必要性:第一很简约,第二数字表示不完……而字母具有高度的抽象性,简洁性,概括性……
接下来思考:① 字母和数有什么相同和不同之处?
学生可能举例:3和a,3就是3,a可以3,-3,0……
② 求3的绝对值,-4的绝对值,a的绝对值呢?-a是负数么?……
③ 用式子表示加法(乘法)交换律……
在不断的追问和应答中,培养学生用结构眼光看世界,发展学生抽象能力和归纳能力,形成从生活到数学的数学眼光,在定义和概念形成的过程中认识式结构.
专家总结:数学抽象包括三个阶段(层次):
简约阶段:将繁杂的实际问题简單化、条理化,感受到可以借助图(还不是图形)或更简单的文字清晰地表达.
如,面对一群跳来跳去的青蛙这一繁杂的事物,利用“一只青蛙一张嘴,两只青蛙四条腿……”这样很简洁、有条理的文字表达,关注一只青蛙的嘴、眼、腿的关系.
符号阶段(对应符号意识):去掉具体的内容,利用概念、符号、关系表述已经简约化的事物.如,可以借助数的概念、字母、符号建立青蛙的嘴、眼和腿的关系:嘴的数量是1,设眼的数量为a,腿的数量为b,则有a=1×2,b=1×4,
这样的表达已经初步把事物关系的本质用数学来表征.
普适阶段(对应模型思想):建立一般法则,进行简单推理,形成数学模型,解释更多具体事物.如,对一只、两只、三只……青蛙的嘴、眼和腿的关系,抽象形成n,2n,4n……这样具有一般意义的数学模型.这三个阶段构成一个从特殊到一般、从感性到理性、从现象到本质的抽象过程.
案例2:以“代数式的值”为例
问题1:代数式2x的实际意义是什么?
问题2:当x=-2,求代数式2x的值.
问题3:x还可以取哪些值?2x的值有什么变化?
问题4:所有代数式的值都会和2x值的变化一样么?举例说明
凡变化必有序,序是从无到有,是数学中的重要特征,对问题的排序,从无序到有序,问题及解决.
案例3:“用二元一次方程组解决问题”为例
用模型表达解问题,发展学生的应用意识和创新意识,促进学生用式、方程、不等式和函数等模型刻画实际问题,在问题解决的过程中,创新策略、优化式结构.
问题1:你能举例说明2x+3的实际意义么?你能求出x的值么?如果不能请你结合例子添加条件,求出x的值.
问题2:你能举例说明方程x+3=4和2x=4的所刻画的实际意义吗?
(注:二元一次方程组中的x表示的是同一个量)
问题3:你能用符号语言表示上述方程的“式结构”么?
有了这些作基础可以展开从方程到实际问题的追问1:你能举例说明方程2x+3=4和2(x+3)=4的所刻画的实际意义么?
再从实际问题到方程:例1:某一天菜场菠菜的价格为:青菜2元/千克,蒜苗4元/千克,结合上述信息便一道应用题,使所列方程为:2x+4(5-x)=12.
2 教学谋划
方程是引导学生理解数式结构的好媒介,可以引导学生用不同符号来理解同一事物的具体数量,充分感受“算两次”思想,感受不同的代数式可以表示同一数量的思想,感受代数式应用的广泛性.
为了充分理解数式结构贯代数,我们可以对整个初中教学进行谋划,比如:
某专卖店销售核桃,其进价为40元/kg,按60元/kg出售,平均每天可售出100kg,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20kg,若该专卖店销售这种核桃想要平均每天获利2240元,每千克核桃应降价多少元?……
2.1 在初中数学“大系统”中进行谋划
七上“用字母表示数”
某专卖店销售核桃,其进价为40元/kg,按60元/kg出售,平均每天可售出100kg,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20kg,如果每千克降价x元,则每千克利润为 元,销售数量为 千克.
七下“整式的乘法——多项式乘以多项式”:
2.3 在初中数学“中系统”中进行谋划
追问1:这个长方形面积能为25m2么?能为30m2?最大为多少?
追问2:总利润能为2250么?总利润能为3000元么?总利润最大是多少元?
新课标对于《根与系数的关系》一节内容提出了更高的学习要求,尤其重视其代数推理过程,为了适应新课标,也为了让学生通过观察数式结构来思考解决问题方法,对于此课定理的形成过程教学设计和过程展示如下:
问题:方程ax2+bx+c=0(a≠0)的两根为x1、x2,请猜想x1+x2、x1·x2與各项系数a、b、c之间有什么关系?
追问1:如何证明?你有哪些方法?
学生容易想到用求根公式将两根表示出来再相加和相乘,化简即得,不做过多赘述.
追问2:方程还可以写成a(x-x1)(x-x2)=0,比较两个方程,能否得到根与系数之间的关系?
一元二次方程的两根式学生不熟悉,可以加入适当问题帮学生理解:
① 我们学习过因式分解解一元二次方程,方程的左边可以写成因式乘积的形式.
② 方程如果有一个根是x1,则方程左边应该有因式?(x-x1)
③ 方程如果有一个根是x1、x2,则方程左边应该有因式?(x-x1)(x-x2)
④ 一元二次方程一般式中二次项系数为a,但是上式展开二次项系数为1,怎么办?(容易想到前面加a即可)
这样就得到两根式,这个过程的探索让学生对于式结构的理解也大有裨益,不应直接忽略.
3 总结
研究数式结构可以把握数量之间的一般关系和规律.在经历用数和字母表示数量,用代数式、方程表示数量关系,用运算和推理判断数与代数式之间的大小关系三部曲后,学生对于代数中的核心要点:“符号”“表示”“运算推理”烂熟于心,运用自如.万物是模型,式有千面终归一;结在其间为关键,构出关系自生长.

