基于问题驱动的“函数”起始课教学实践与思考
陈敏婕 叶旭山

摘 要:问题是数学课堂教学的起搏器和动力源,以问题驱动数学概念教学,往往能够调动学生自主建构概念的积极性.基于这样的教学理论,围绕“函数”起始课核心概念进行教学,尝试根据逻辑结构设计问题串,以问题驱动概念教学,引发学生深度思考,在学生“再认识”“再创造”的过程中,深化对函数概念本质的认识.
关键词:函数;问题驱动;核心概念;起始课
《义务教育数学课程标准(2022年版)》中明确指出“重视发挥情境设计与问题提出对学生主动参与教学活动的促进作用,使学生在活动中逐步发展核心素养”.可见,问题提出是促动数学课堂教学活动有效发生、培育学生核心素养的重要路径.这就要求教师在课堂教学设计中应注重问题的驱动、引领,提升学生参与活动的质量.因此,笔者在《函数》起始课的教学中,尝试进行了以问题驱动来助力函数概念理解的教学探索.
1 背景分析
世界是运动变化的,函数是研究运动变化的重要数学模型.以探索简单实际问题中量的变化为背景,经历“找出常量和变量,建立函数模型表示变量之间的单值对应关系”的过程,自然形成函数概念,体现了抽象的思想、变化和对应的思想,以及建模思想.
本节内容主要包括:常量和变量的意义,函数的概念及其三种表示法.考虑到函数概念尤为抽象,本课从具体的现实情境入手,分析变化过程中量的变化,抽象出变量的概念,用对应的观点分析变量之间的关系,并以此为基础,归纳各情境之间两个变量关系的共性特征,抽象出变量的单值对应关系,进而归纳出函数的概念.通过对情境的再认识,梳理函数的三个要素(自变量、因变量、对应关系),并借助形象直观的方式,助力学生理解函数概念的本质特征.
2 教学实践
2.1 问题情境
情境1:甲、乙两地相距600km,列车以300km/h的速度从甲地匀速驶往乙地.
问题1:在列车行驶过程中,哪些量保持不变?哪些量是变化的?
问题2:你能说说列车的行驶路程skm与行驶时间th的关系吗?
追问:时间的变化对路程有什么影响?具体说一说.
设计分析:从学生较熟悉的行程问题出发,学生很容易分析出在这个变化过程中,不变的量有“速度、总路程、总时间”,变化的量有“行驶时间、行驶路程、剩余路程”,并顺势引出常量与变量的概念.
问题2引导学生找寻行驶路程与行驶时间这两个变量之间的关系,学生最先想到的是行程问题中蕴含的等量关系,即s=300t.进一步追问在这个变化过程中,随着时间的变化,路程有什么影响,并引导学生举例说一说,学生自然地想到当t=1、当t=2时对应的行驶路程s的值.第一个情境的细致分析与解读为后续情境2、3的研究方法提供了样例.
问题3:在这个变化过程中,哪些量是变量?
追问:这两个变量之间有什么联系?
设计分析:引导学生自主分析情境2中涉及的变量,并尝试找出两个变量之间的联系.部分学生困惑这两个变量的关系并非像问题1中有明确的变化规律,教师需适时引导,帮助学生排疑解虑,明确这两个变量的依赖关系,也是一种内在联系.如“当x取定一个值时,y也有一个值和它对应”,突出函数的本质,剥离“用式子表示数量关系”这一非本质属性.另外,此處的对应还出现了“多对一”的情况,丰富学生对函数中“对应”的理解.
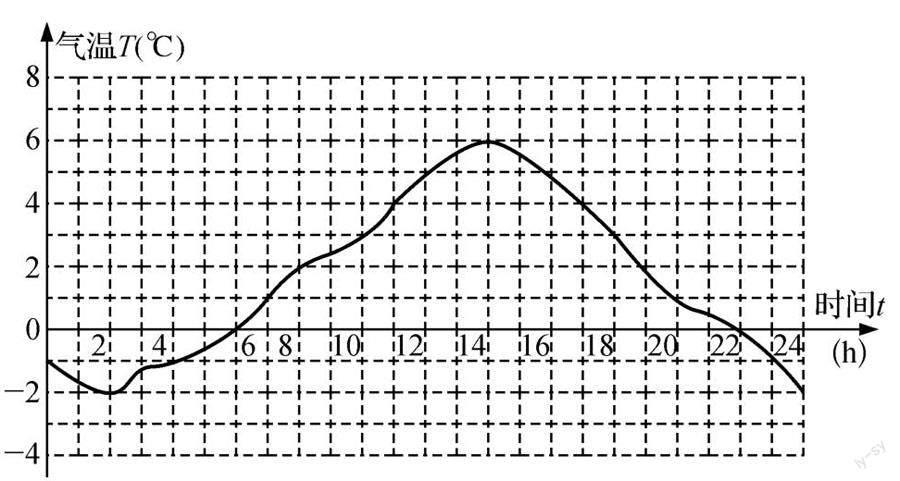
情境3:气象站测得南京某日气温变化图:
问题4:请你描述图中气温T(℃)和时间t(h)的关系.
设计分析:在经历了情境1、2中变量关系的分析后,让学生自主描述情境3中两个变量之间的关系,再度感受“随着t的变化,T也变化;当t确定时,T也随之确定.”也就是“当t取定一个值时,T也有一个值和它对应”,为函数概念的归纳做铺垫.
2.2 概念生成
问题5:上述情境有什么共同特征?
一般地,在一个变化过程中的两个变量x和y,如果对于x的每一个值,y都有唯一的值与它对应,那么我们称y是x的函数,x是自变量.
设计分析:启发学生找寻三个情境的共同特征,并尝试用文字语言归纳,学生之间不断补充完善,生成函数概念.
问题6:重回情境,从函数角度分析变化过程中两个变量的关系.
追问:这些对应关系从哪里看出来的?
设计分析:理清函数概念后,用函数的眼光重新看待上述三个情境中两个变量的关系,指出谁是谁的函数,再度感受函数概念中的“单值对应”.借助于工具图“数值转换机”,使得变量之间的函数关系得以直观形象地呈现,帮助学生更好地理解函数的本质.此外,三个情境恰好也展现了函数的三种表现形式,教师适时点拨.
2.3 巩固应用
问题7:举一个存在函数关系的例子.
设计分析:学生尝试举例,有从现实情境描述的,有从数学内部找寻的,引导学生进行自我评价和相互评价,感受身边丰富的函数素材,深化对函数概念的理解.
问题8:用20m长的绳子围一个矩形.你想研究哪些量?
追问1:这些量之间存在函数关系吗?
追问2:你还能提出什么问题?
设计分析:提供定周长的绳子围矩形的素材,引导学生自主找寻其中的变量,并分析是否存在函数关系.学生容易想到的量有长、宽、面积,启发学生进一步提出问题,如定周长的矩形面积何时最大等,增强学生提出问题与分析问题的能力.
2.4 拓展延伸
问题9:已知矩形的面积为100.续写你想研究的内容.
设计分析:沿着例题的研究路径,引导学生自主探索在定面积的矩形这一背景下,值得研究的量以及隐藏的函数关系等.
2.5 小结反思
问题10:通过本节课的学习,令你印象最深的是什么?
追问:由函数,你想到了什么?
设计分析:引导学生回忆本节课的研究过程,以及印象最深的环节.教师对学生谈到的认识总结、归纳,提炼函数概念可以用“一句话、一张图”助力理解.追问启发学生展开进一步联想,如想到代数式、方程、函数的应用等,鼓励学生用整体的、联系的、发展的眼光看问题.
3 教学反思
3.1 设计进阶问题,驱动学生深度思考
问题情境是教学活动的起点.开篇通过熟悉的行程问题中这一变化过程引入,启发学生用变化的眼光思考现实世界.三个情境中问题的设问方式分别是“你能说说列车的行驶路程skm与行驶时间th的关系吗”“这两个变量之间有什么联系”“请你描述图中气温T(℃)和时间t(h)的关系”.设问方式层层递进,旨在提高学生自主分析问题和解决问题的能力.情境问题的设置相得益彰,方使得共性特征的探析水到渠成,凸显了函数概念的形成过程.而后用函数的观点重新审视三个情境,引导学生用数学的思维思考现实世界.
通过学生举函数关系的例子,深化学生对函数概念的理解.如学生有谈到烧水过程中,水温与时间的变化过程,教师顺势引导烧水的两段历程,一段是水烧开以前温度随时间的变化,另一段是水烧开后水温保持100摄氏度,再追问学生水温是否是时间的函数,加深了学生对于概念本质的理解.学生举出了很多有价值的例子,学生的思维在沸腾.
3.2 借助图形直观,实现抽象概念可视化
数形结合思想是一种重要的数学思想,它可以将抽象的数学语言、数量关系与直观的图形相结合,以形助数、以数辅形,数形结合,相辅相成.三个情境中,不断强调、凸显两个变量之间的关系,让学生充分感受“对于x的每一个值,y都有唯一的值与它对应”.这里输入一个x,输出一个y,有的学生已经感受到像有个“程序”在牵引着这两个变量,说明学生的内心已然在编织一幅形象直观的图来理解函数概念.教师抓住学生闪现的星光,顺势理清这张函数解析图——数值转换机.
这张图呈现了概念中的三要素,自变量x正如原料,因变量y恰似产品,函数的对应关系则是机器的运行原理,这正是函数的内核.后续例题环节,分析素材中的变量是否存在函数关系,仍可以通过两个角度来阐述,即函数的文字概念与数值转换机的形象表述.一句话、一张图,道清了函数两个变量之间的关系.函数模型可视化,于生而言,是一份难忘的记忆,同时使得对函数概念的理解更加深刻.
3.3 设置开放性问题,拓展思维空间
给学生思考的空间与时间,让学生的思维动态触发、进阶、升华.在例题环节,教师只提供背景素材,让学生自主找寻想研究的量,并分析其中的函数关系,提出想要进一步研究的问题.学生亲历找变量、构建函数模型,用数学的语言表述现实世界,其建模素养在悄然提升.
开放式的小结,意在培植学生的发散性思维.有的学生由函数想到了代数式,函数的右边就是关于自变量的代数式,并且类比代数式的样子,进一步猜想还可能研究的函数表达式的类型.有的学生想到方程,如果把两个变量看成是两个未知数,函数表达式可以看成一个二元方程,如果给其中一个变量赋值,那么就变成了一元方程,可以解出对应的另一个变量的值.无形中为后续函数各类型的研究以及与方程、不等式关系的研究埋下伏笔.
参考文献:
[1] 中华人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大學出版社,2022.
[2] 喻平.著名特级教师教学思想录[M].南京:江苏教育出版社,2012.
[3] 李光红.对问题深入思考 促学生“深度学习”[J].中学数学教学,2019(3):25-27.

