基于离散双向联想记忆神经网络的多元通信系统
陈伟康,翟其清,王友国*
(1.南京邮电大学 通信与信息工程学院,南京 210003;2.南京邮电大学 理学院,南京 210023)
0 引言
自从1982 年Hopfield[1]提出了 经典的Hopfield 神经网络,联想记忆网络开始成为神经网络的重要分支,它的理论研究和应用在近几十年取得了长足的发展。许多新型的神经元模型以及组成的神经网络被提出。神经网络采用并行计算和分布式数据处理,在图像处理、模式识别、故障诊断、信息传输、人工智能等方面[2-7]有非常成功的应用。
在通信与信号处理领域,Zhang等[7]在幅值相位型离散Hopfield 神经网络的基础上引入混沌神经网络算法,提高了盲检测多进制相移键控(Multiple Phase Shift Keying,MPSK)信号的性能。刘玉龙等[8]发现利用Hopfield 神经网络可以在一定条件下解决多用户正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)通信系统的子载波分配和比特自适应加载的资源分配最优化问题。Duan等[9]在研究基于Hopfield 神经网络的信号传输系统时发现,适量的噪声可以改善系统的性能,并且当信号被重尾噪声破坏时,具有大量神经元的系统在每比特输入信噪比较低时优于匹配滤波器。于海斌等[10]提出一种基于双向联想记忆(Bidirectional Associative Memory,BAM)神经网络的按位加权编码策略,使网络对不满足连续性的样本模式集具有良好的联想能力。
在图像识别与处理领域,Zhang等[6]改变激活函数以提高基于Hopfield 神经网络的盲检测算法的性能,以解决无人机运动模糊图像恢复的问题。潘园园等[11]利用Hopfield 神经网络进行手写数字识别,并发现适量噪声有助于数字图像恢复得更清晰。蔡利梅等[12]研究了基于BAM 神经网络的车型识别问题。Cheng等[13]提出一种基于竞争性Hopfield 神经网络的并行无监督方法进行医学图像分割,取得了更优的效果。王元莉[14]提出了一种基于BAM 神经网络的快速增强算法识别带噪声污染的字符,具有很好的实时性和容错性。
神经网络能够实现联想记忆,因为系统在一定条件下存在稳定的平衡点或周期解,吸引域中的任意初始状态都将收敛到相应的平衡点或周期解。将稳定的平衡点或周期解称为记忆模式,初始状态收敛到相应平衡点或周期解的过程称为联想并恢复记忆的过程。为了探究和利用联想记忆神经网络的这种性质,本文基于BAM 神经网络构建了一种多元通信系统以传输多元信号。多元信号被调制为带有幅值的初始状态向量,在码元持续时间里,不断输入系统中,经过神经网络的循环迭代和以码元间隔为周期的采样,假定是在无噪无损的信道中传输,最终在接收端判决译码。在文献[9]中的基于Hopfield 神经网络的二元通信系统中,向系统神经元加入适量高斯噪声有助于提升传输性能,还展示出了联想记忆神经网络中的随机共振现象[15-17]。因此本文也尝试向神经元中加入高斯噪声,并研究噪声对该通信系统译码性能的影响。最后,将本文系统应用于传输图像压缩编码,并通过图像相似度这一指标,探究噪声对系统译码恢复图像的影响。
1 BAM神经网络多元通信系统
1.1 BAM神经网络
BAM 神经网络由Kosko[18]于1987 年提出,在各种联想记忆网络中比较常用。不同于Hopfield 神经网络的自联想,BAM 神经网络可以实现双向异联想。BAM 是一种双层双向网络[19],如图1 所示。当向其中一层输入信号时,另一层可得到输出。初始输入可以作用于网络的任一层,信息可以双向传播,没有明确的输入或输出层。
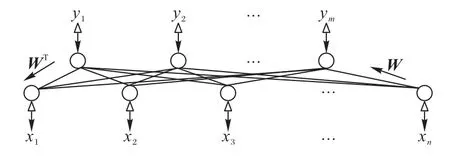
图1 BAM网络的拓扑结构Fig.1 Topological structure of BAM network
BAM 网络联想的过程是网络从动态到稳态的过程。对给定权值矩阵的BAM 网络,当第p个网络的记忆向量Xp作用于输入层时,t=1 时刻该层的输出X(1)=Xp通过加权矩阵W传到输出层,由该侧神经元的激活函数fy(·)进行非线性变换后得到t=1 时刻该层的输出Y(1)=fy[WX(1) ];再将该输出通过加权矩阵WΤ从输出层传回输入层作为下一时刻的输入,通过输入层神经元的激活函数fx(·)进行非线性变换后得到t=2 时刻该层的输出X(2)=fx[WΤY(1) ]=fx{WΤ[fy(WX(1))]}。这个过程一直进行到所有神经元的状态不再发生变化为止,此时的网络状态称为稳态,对应的输出层输出向量Yp是记忆向量Xp经双向联想后所得的结果;反之,将记忆向量Yp作用于输出层,最终也能在输入层联想出Xp。
1.2 系统定义与参数说明
本文基于图1 的BAM 网络构建了如图2 所示的多元通信系统,由信号映射器、BAM 神经网络、采样器、无损信道和判决器组成,其中Z-1为时延单元。BAM 网络的输入层有n个神经元,输出层有m个神经元,共计N=n+m个神经元。输入层到输出层的权值矩阵为W,输出层到输入层的权值矩阵为WΤ。令神经元激活函数为双曲正切函数f(·)=tanh(·),输入层的网络状态向量为X(t),输出层的网络状态向量为Y(t),状态向量的分量xi(t)、yj(t)表示神经元i、j在t时刻的状态,状态向量及其分量定义如下:

图2 基于BAM神经网络的多元通信系统Fig.2 BAM neural network based multivariate communication system
其中:ε为陡度参数;Wij是神经元i到j的突触权重;θi是神经元i的激活阈值,若阈值为0,网络的能量函数定义为E=-XΤWΤY;si(t)为输入层的输入信号;ηi(t)是均值为0 且独立同分布的高斯噪声分量。网络具有M对记忆向量(Xμ,Yμ),μ=1,2,…,M,x∈{ -1,1}n,y∈{ -1,1}m,分别对应M进制信号,假设用于设计网络的M对记忆向量相互正交:
其中,p和k代表记忆向量的索引标号。
采用Hebb 规则,即外积和法设计网络的权值矩阵W:
在接收端,设计一个判决规则,网络输出端状态向量Y(t)和记忆向量Yμ之间的重叠量mμ定义为:
通过该重叠量mμ(t)可以将状态向量Y(t)的m维空间V划分为M个子集V0,V1,…,VM-1,Vμ={Y|mμ(t) ≥mj(t) }表示记忆向量Yμ对应的吸引域,当调制向量AXμ输入网络时,网络状态向量Y(t)在统计意义上将主要落入吸引域Vμ。然后,在采样时间t=jTb处,通过观察网络状态向量Y(t)落入哪个子集Vμ来解码M进制数字。相当于计算重叠量mμ(jTb)来解码,如果Y(t)∈Vμ,就解码为与Yμ对应的码元。根据上述判决规则,本文通过计算差错概率Pe来度量系统传输的译码性能,Pe定义如下:
其中:p(i)为M元信号中数字i的先验概率,由实验的信号集经过统计得到,本文使用先验概率等概的多元信号集表示当输入数字为i时,解码为j的概率,由系统的译码结果和原始输入信号集比较,然后统计错误码元得到。
2 BAM多元通信系统的译码性能分析
2.1 传输二元信号的译码情况
首先,探究系统传输二元信号时的译码情况,该信号序列由{0,1}组成。假设输入层神经元个数n=4,输出层神经元个数m=2,取两对记忆向量(X0,Y0)、(X1,Y1),其中:X0=[1,-1,1,-1]Τ;X1=[ 1,1,-1,-1]Τ;Y0=[ 1,-1]Τ;Y1=[ 1,1]Τ;权值矩阵W由这两对记忆向量生成。如图2 所示,携带数字0 和1 的先验概率为p(0)和p(1)的二元信号,被调制为在时间间隔jTb≤t≤(j+1)Tb上持续的向量AX0和AX1作为输入信号,其中:A是调制幅度;Tb是码元间隔。系统的其他参数设置如下:陡度参数ε=0.03,神经元阈值θ=0,码元间隔Tb=1。
图3 给出了不同参数下系统的译码差错概率Pe曲线。从图3(a)可以看出:在码元间隔不变时,对于A<1.0 的二元信号,即弱调制信号,系统传输的译码效果较差;但是向系统神经元添加高斯噪声时,随着噪声强度增加,差错概率Pe先减小后增加,出现随机共振现象,最佳噪声强度范围为0.4~0.5。随机共振现象的出现对A的值有要求,当A≥1.0 时,虽然系统Pe在降低,但噪声对系统的消极作用占主导地位,这是由于A的增大也导致了输入信号的能量增大,此时信号的传输效果比较好,而噪声只会影响传输效果。因为随机共振往往对弱的信号有积极功效,随着信号幅值的增加,随机共振的功效逐渐减弱直至消失。
在A=0.8 时,尝试增大信号的码元间隔Tb,如图3(b)所示。可以看出,随着Tb增大,系统的Pe进一步降低,随机共振现象更加明显,最佳噪声强度在0.3 左右。对于较大的Tb,网络的输出状态向量有较长的时间收敛到对应记忆模式的吸引域内,导致判决时对应的重叠量mμ(t)最大,从而进行正确的译码判决。

图3 不同噪声下A与Tb对系统Pe的影响Fig.3 Influence of A and Peon Pe of system under different noise intensities
2.2 传输多元信号的译码情况
由于BAM 网络的存储容量不大于min(n,m),所以对网络取输入层n=32 个神经元、输出层m=16 个神经元,以满足对所选进制数M=2、3、4、8、16 中最高16 的条件。对于M元信号,网络选取M对记忆向量。设置码元间隔Tb=1,调制幅度A=0.5,其他参数不变,仿真结果如图4 所示。可以看出,对于多元信号,该系统仍然出现了随机共振现象,但是随着M的增加,Pe也在增加。当BAM 网络存储更多的记忆向量时,网络平衡点对应的吸引域个数也随之增加,在有限的时间里,系统输出端状态向量Y(t)很难快速地在不同吸引域之间跳转并落到正确的吸引域内,从而导致接收端的误判,导致差错概率Pe增加。

图4 不同噪声下传输不同进制信号时系统的PeFig.4 Pe of system when transmitting signals with different radix numbers under different noise intensities
为了探究神经元数量对系统传输多元信号的影响,用(n,m)表示n个输入层神经元、m个输出层神经元,具体取(16,8)、(32,16)、(64,32)、(128,64)、(256,128)、(512,256)这6 组,对三元信号进行仿真,其他参数与图4 一致,仿真结果如图5 所示。随着神经元数量的增加,系统的Pe大幅降低,并且随机共振现象非常明显,在神经元数量为(512,256)、噪声强度为0.75 时,Pe约为0.002。结果表明增加神经元数量可以显著降低传输多元信号的系统差错概率,原因如下:1)随着神经元数量的增加,网络的平衡点对应的吸引域范围变大,输出端状态向量更容易落在正确的吸引域内,所以判决时的错误率减小;2)从通信的角度来看,信号的传输功率NA2Tb和每比特输入信噪比NA2Tb/σ2η也随着神经元数N的增加而增加。

图5 不同噪声下传输三元信号时不同神经元数的系统Pe Fig.5 Pe of system with different neuron numbers when transmitting ternary signals under different noise intensities
同时,讨论了码元间隔Tb对系统传输多元信号的译码性能影响,取图4 中进制数M=4 和神经元数(128,64)进行仿真,得到如图6 所示的结果。发现Tb对多元信号的传输仍然具有影响,当Tb逐渐增大时,系统的差错概率Pe在相应的最佳噪声强度下越来越小。比如当Tb=5 时,在噪声强度0.25~0.5 范围内,Pe可以达到0 的最佳情况;当Tb较大时,系统的计算复杂度会增加,影响传输效率。实际系统中可能会在传输效果和传输效率之间采取一种折中的方法。
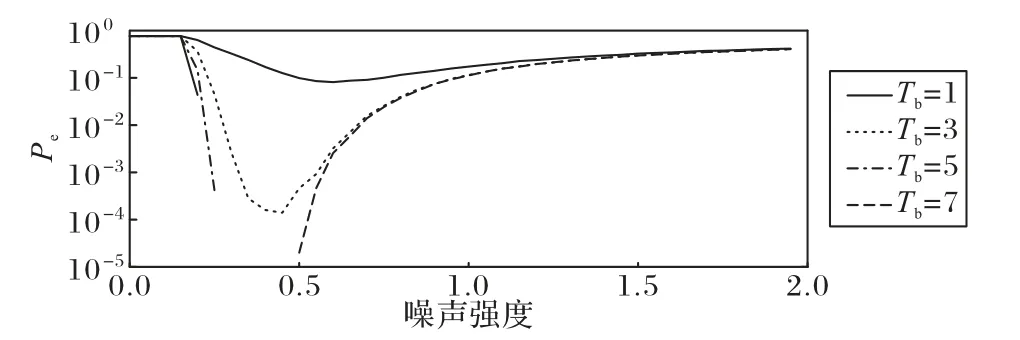
图6 不同噪声下码元间隔对系统传输多元信号的影响Fig.6 Influence of code element interval on system transmission of multivariate signals under different noise intensities
3 BAM神经网络在图像压缩中的应用
本文以图像压缩为例,采用哈夫曼压缩编码方式。如果直接用二进制码元表示灰度图像,每个像素点需要8 位,直接传输的效率太低,因此先进行信源编码。为了探究基于BAM 的通信系统传输多元信号的效果,选择三元哈夫曼编码,码元由{0,1,2}组成,对图7(a)所示的灰度图像Lena 进行压缩编码。图像大小为512× 512,取系统神经元数量为(512,256),其他参数和图4 一致。首先根据哈夫曼编码得到的码字,将图像转换为由{0,1,2}组成的码元集,作为系统的输入信号集;然后向系统中加入不同强度的高斯噪声,经过系统传输得到输出信号集;最后通过译码恢复图像。
从直观感受和图像相似度对实验结果进行分析,采用均值哈希算法评估图像的相似度。不同噪声强度下的仿真结果如图7 所示,当ση=0.25 时,译码效果最差,恢复的图像根本无法识别;当ση=0.50 时,译码的图像可以识别;当ση=0.75 时,恢复的图像效果最佳;ση=1.00 时效果与0.75 类似;随着ση进一步增加到1.50,译码效果又开始变差。从图8 可以看出,ση=0.75 时,图像相似度最低,效果最优。实验结果表明噪声在BAM 神经网络通信系统传输图像中有积极功效,进一步验证了BAM 通信系统和随机共振在实际应用中的可实现性。

图7 不同噪声强度下的译码图像Fig.7 Decoded images under different noise intensities
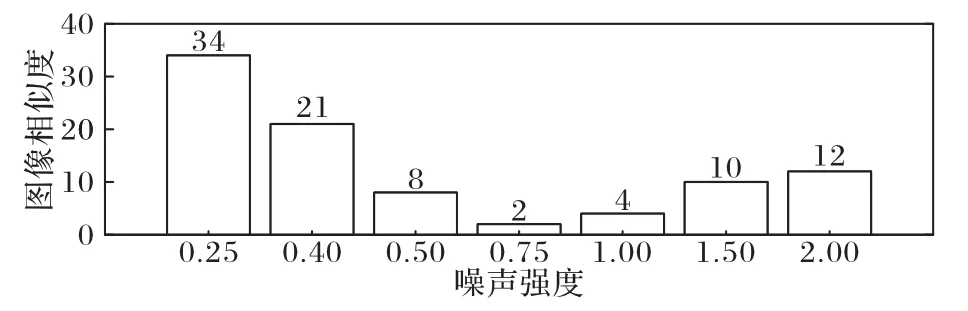
图8 不同噪声强度下译码图像相似度Fig.8 Decoded image similarity under different noise intensities
4 结语
本文基于已有的对Hopfield 网络通信系统的研究,进一步利用离散BAM 神经网络构建了一种用于多元信号传输的通信系统。考虑随机共振这一在非线性系统中可能存在的现象,在一定条件下,向系统神经元加入适量的高斯噪声,使系统的传输效果得到一定改善;同时,改变输入信号的幅值和码元间隔也会对系统传输产生影响。进一步研究了系统传输不同进制的信号,发现对高进制信号的传输效果不佳,于是采用增加系统神经元数量的方式,发现可以有效降低系统的差错概率。最后,结合实际应用,研究了本文系统传输图像压缩编码时噪声对图像解码质量的改善的问题,体现了随机共振的实用性,为进一步研究BAM 神经网络以及其他联想记忆网络做了基础工作。此外,关于噪声对系统起增益作用的临界幅值、实际系统中码元间隔和神经元数量的折中选取,这些问题值得进一步研究。

