基于深度学习的标签噪声学习算法综述

伏博毅，彭云聪，蓝鑫，秦小林*

（1.中国科学院 成都计算机应用研究所，成都 610041；2.中国科学院大学 计算机科学与技术学院，北京 100049）

0 引言

深度学习以大规模数据集为前提，在图像分类、目标检测、文本分析等领域取得了显著的成功，而成功的关键在于现有的海量标记数据集，如MS COCO（MicroSoft Common Objects in Context）［1］和ImageNet［2-3］等大规模数据集。然而，实际场景中收集高质量的大规模数据集既耗时又昂贵。为降低成本，构建数据集的过程会利用某种程度的自动标注或众包标注，而这些技术本质上容易出错［4］，从而引入带有标签噪声的低质量数据。此外，Northcutt等［5］发现，在大型通用数据集如ImageNet 上也存在标签噪声，ImageNet 验证集中存在多达2 916 个标签错误，占总验证集的6%。

研究表明，尽管深度学习网络在对标签噪声的处理上相对稳健［6-7］，但这些强大的模型依然存在噪声过拟合的情况，极大地降低了模型的泛化性能。此外，如果标签噪声大量出现，它们可能会破坏当前模型的评价体系。例如，各行业从业者依赖于带有噪声的真实数据集，如果用它们进行训练、验证，可能会得出错误的模型。

目前标签噪声问题已经越来越受到重视，因为它们可以显著影响学习到的分类器的准确性［8-10］。如何从含有标签噪声的数据集中学习成为现代深度学习任务的一项重要研究。因此越来越多的学者开始针对噪声数据进行研究，遗憾的是，传统的正则化技术，例如数据增强［11］、Dropout［12］等方式，并没有很好地处理标签噪声问题。即使上述所有正则化技术都被激活，在干净数据和有噪声数据上训练的模型之间的测试精度差距仍然很大。在存在噪声标签的情况下，模型如何获得良好的泛化能力充满了挑战性。本文介绍了最新的标签噪声学习技术的进展，以缓解标签噪声带来的影响。

本文首先详细阐述了标签噪声学习问题的来源、分类和影响，然后依据机器学习的不同要素将它归纳为基于数据的标签噪声学习算法、基于损失函数的标签噪声学习算法、基于模型的标签噪声学习算法与基于训练方式的标签噪声学习算法，有助于对算法进行评价；接着提供了一个带标签噪声样本学习的基础框架，分析了各种应用场景下标签噪声问题的处理策略，以便众多相关研究者参考和借鉴；最后，对标签噪声学习技术进行总结，给出了一些优化思路，并展望了标签噪声学习算法面临的挑战与未来的发展方向。

1 标签噪声

1.1 问题描述

标签噪声问题可以定义为在有监督学习下，假设带噪数据集为D={(x1，y1)，(x2，y2)，…，(xn，yn)}∈(X，Y)n，噪声分布（未知）为(X，Y)n，目标是寻找最佳的映射函数f：X→Y［13］。损失函数常用于评估分类器的性能，可以定义损失函数L(f(x)，y)以衡量分类器的预测性能。在D上的经验风险R定义为：

经验风险最小化结果为：

大部分研究采用随机噪声对标签噪声建模，可以分类为对称标签噪声和非对称标签噪声；而实际上数据标注错误往往取决于实例和识别的难度，存在实例相关噪声［14-15］。标签噪声模型可表述为：

对称标签噪声可以理解为真实标签yn以相同的概率ηxn，i=η被翻转为其他标签i。非对称标签则是真实标签yn以不同概率ηxn，i被翻转为其他标签i，而真实标签yn会以更高的概率被标注为某一特定类标签，即1 -ηxn＞ηxn；且某个类更有可能被错误地标注为特定的标签，即i≠yn，j≠yn，ηxn，i＞ηxn，j。对称标签噪声的生成过程完全随机，生成的错误标签与真实标签和实例特征都不相关，而实例相关噪声生成的错误标签只与实例特征相关，依赖额外的较强的假设，某个类更有可能被标注为与特征相关的噪声标签，即

如果一个损失函数L(f(x)，y)满足式（4），那么该损失函数是对称的。常数C表示遍历所有类别的总损失和。具有对称性的损失函数，具有一定的抗噪能力［16］。

基于噪声标签模型和以上不同噪声标签的定义，对于一个对称损失函数L(f(x)，y)，噪声情况下的经验风险R可以表示为：

对称标签噪声的经验风险R为：

其中，RL(f)为干净数据集的经验风险。对于对称标签噪声，是一个常数，其中，v是一个固定向量。当即和RL(f)线性相关，所以它们的最优解相同，即对称标签噪声情况下的风险最小化的模型f*和干净数据集下的风险最小化模型f相等，这种情况下损失函数L(f(x)，y)具有鲁棒性，对标签噪声具有很好的抗噪性。

对于非对称噪声，经验风险R表达式为式（7）。如果要满足相等的条件，则需要满足RL(f*)=0，1 -ηy-ηy，i＞0。

但是，对于带噪数据集，仅通过经验风险最小化来处理标签噪声往往不够，因为损失函数L(f(x)，y)的对称条件限制过多，无法找到凸函数，导致优化困难，且经验风险最小化不足以处理标签噪声的多样性。因此接下来将会从数据本身、损失函数的修改、模型结构以及训练方式介绍一些其他的标签噪声处理方法。

1.2 标签噪声的来源

实际场景中标签噪声的一大来源是网页爬取等各种自动标注方法［17-18］。标签噪声还存在于诸多应用场景：在线查询［19］，在查询某一个目标的图像时，存在不属于同一个类的噪声样本；众包标注［20］中存在的非专业标注带来了噪声标签；对抗性攻击［21］会在原始样本中加入噪声以生成对抗性样本；医学图像［22］的数据本身存在不确定性的医疗任务，领域专家给出的不同的诊断结果存在标签噪声。

从含有标签噪声的数据集中学习已经成为深度学习应用的一个发展方向，通过研究标签噪声对模型的影响发现，标签噪声产生的原因很多，主要可以归结为4 类：1）没有充足的信息来标注可靠的标签［23］，例如用简单有限的语言描述物体，则获取的信息量会减少。2）专家在标注标签时也可能发生错误［24］，如数据集质量较低导致分辨率降低，专家很难正确标注所有数据。3）标注任务很主观，不同的人标注数据的角度不同，可能会得到不一致的结果［25-26］。4）数据编码或通信问题有可能引起标签错误，如在垃圾邮件过滤中，反馈机制的误解和意外点击都会引起标签噪声［27］。

1.3 标签噪声的影响

在实际的数据集中，标签噪声难以避免，这会带来以下几方面的影响：1）标签噪声降低了模型预测的能力。如在自适应增强（Adaptive boosting，Adaboost）算法中，模型往往会给被标记错误的样本更大的权重，导致模型的分类能力下降［28］。2）标签噪声可能会增加训练特征的数量和模型复杂度。如受标签噪声影响，决策树节点的数量明显增加，增加了模型的复杂度［29］。3）标签噪声可能会改变观测类别出现的频率［30］。如研究某一人群中特定疾病的发病率，那么该人群的估计可能受到标签噪声的影响。4）在特征选择或特征排序任务中也会存在标签噪声的影响。

另外，过度参数化的神经网络有足够的容量存储，因此带有标签噪声的大规模数据集，导致它们的泛化性能较差。因此，鲁棒的标签噪声学习算法已经成为深度学习应用中一项重要而富有挑战性的任务。

2 标签噪声算法

标签噪声学习算法的鲁棒性可以通过多种方式加强，图1 为本文对最近的标签噪声算法的分类和总结概述，大多数方法使用监督学习，对标签噪声具有良好的抗噪性。本文依据机器学习的不同要素将基于深度学习的标签噪声算法归纳为四类：1）基于数据的标签噪声算法，旨在从带噪数据集中识别真正标签，筛选出错误标签样本；2）基于损失函数的标签噪声算法，旨在修改损失函数使算法对噪声鲁棒或缓解过拟合噪声标签；3）基于模型的标签噪声算法，通过设计结构鲁棒的模型学习噪声或者对模型进行正则化以提高模型泛化能力；4）基于训练方式的噪声标签算法，引入半监督学习方法进一步提高模型对噪声的鲁棒性。同时，图1 还将深度学习最新的方法根据以上四类进行划分。

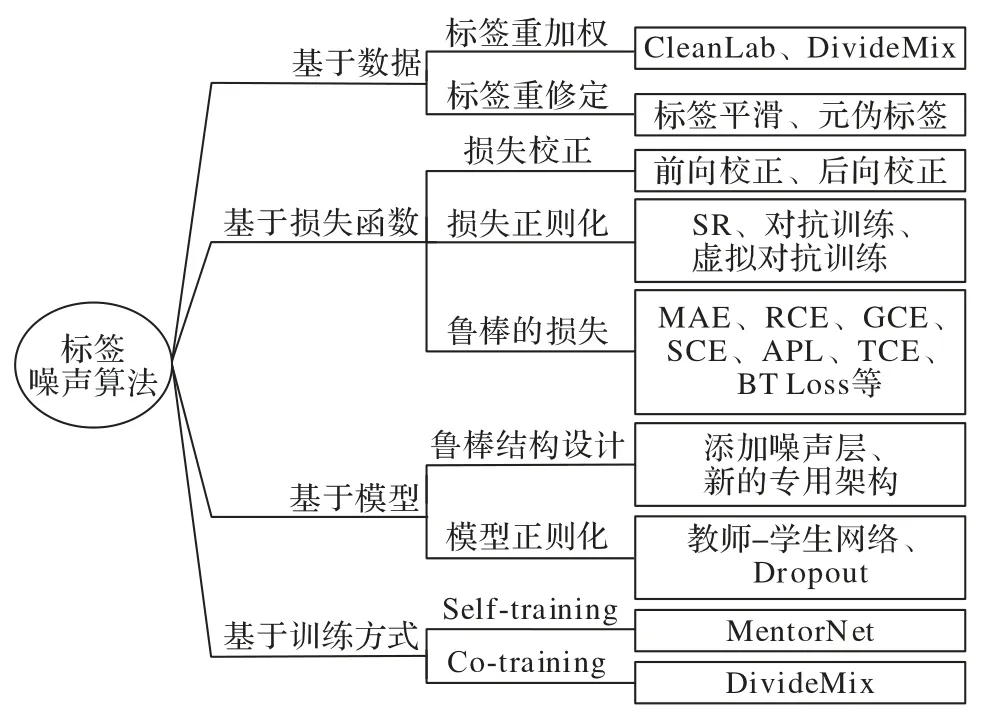
图1 标签噪声学习算法分类Fig.1 Categories of label noise learning algorithms

2.1 基于数据的标签噪声算法

本节主要介绍数据处理的标签噪声学习算法。对于标签噪声问题，最简单的做法是找出疑似标注错误的样本，通过降低权重或者直接剔除以改善学习效果。另外，如果能估计噪声转移矩阵或采用其他方式，进行一定程度的标签修正，就能够在标签噪声情况下得到更好的效果。因此，将基于数据的标签噪声学习算法归纳为以下两种类型：样本重加权、标签重修正。

2.1.1 样本重加权

样本重加权指通过样本损失值、模型输出的样本概率、梯度等信息，找出疑似错误标注的样本，通过赋权重为0 以剔除可能样本，或采用更平滑的手段——降低疑似样本的权重来清理标签噪声。

样本重加权主要通过分区和迭代对标签噪声进行过滤。基于分区的方法制定分区规则，然后过滤不同区域的标签噪声。张增辉等［31］提出了动态概率抽样的方法，通过统计样本的标签置信度对样本分区；陈庆强等［32］采用欧氏距离度量样本分布的密度以划分不同的区域，按照分区采用不同的规则过滤标签噪声。基于迭代的方法通常利用半监督的方法清理标签噪声。孟晓超等［33］结合高斯过程模型和主动学习，迭代地清理标签噪声，相较于监督分类方法，能够保持原有数据的完整性。此外，标签重加权方法需要对标签进行重要性估计。陈倩等［34］通过无约束最小二乘重要性算法估计标签重要性，结合Self-training 和标签重要性进行半监督训练，对样本进行重加权分类。这些方法依赖于分区规则和迭代阶段，可能会错误地过滤掉噪声样本。

为了更方便地筛选出标签噪声，Northcutt等［35］提出了置信学习（Confidence Learning）框架CleanLab，如图2 所示。该框架旨在利用带有标签噪声的数据训练模型，得到的模型能够识别具有错误标签的样本，学习标签噪声并清理标签噪声。该框架主要分为三个步骤：首先评估样本的噪声标签和真正标签的联合分布；然后识别错误标签的样本；最后筛选出错误标签的样本后，对样本进行重加权并重新加入训练。在真实充分条件下，置信学习框架可准确地发现标签错误，并准确地估计噪声和真实标签的联合分布。

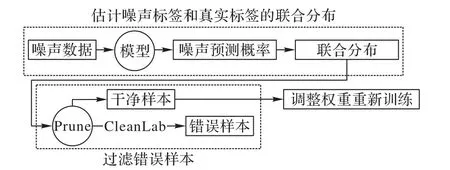
图2 置信学习框架Fig.2 Confident learning framework

从另一角度，Li等［36］提出基于样本损失的DivideMix 算法。该算法的核心思想在于当带噪学习的模型较合理时，正常样本和错误标注样本的损失值会呈现显著性差异。DivideMix 采用高斯混合模型对样本的损失值进行聚类以划分样本，真实标签的干净样本为有标签集合，均值较小；噪声标签的样本为无标签集合，均值较大，并以半监督的方式在两个样本集合上进行训练。

上述两种基于预测概率和损失的方法十分依赖带噪学习的模型性能，并且需要合理地微调超参。与上述重加权方法不同，Ren等［37］提出在附加干净无偏验证集情况下的重加权算法，不需要调节超参。在每一个训练迭代中，检查训练损失平面上部分训练样本的下降方向，根据验证损失平面下降方向的相似性对样本进行重加权。

样本重加权方法比较容易适应训练集偏差和标签噪声，是解决标签噪声问题比较流行的一种方案，但是需要潜在的检测过程以估计噪声模型。

2.1.2 样本重修正

标签重修正是对样本标签进行一定程度的修改，达到在带噪学习中保持良好性能的方法。标签平滑（Label Smoothing）常用于提高深度学习模型在噪声数据集上的性能［38-43］。标签平滑将原始标签按式（8）进行修改：

与传统的估计标签转移矩阵以校正每个样本损失的方法不同［44］，标签平滑相当于向标签注入对称噪声，不仅在实验上取得较好的效果，Lukasik等［45］在理论上也证明了标签平滑可以视作一种正则化方法，即可以使模型权重收敛于小范数解。另一方面，对噪声样本生成伪标签能够充分利用所有的样本信息。余孟池等［46］利用训练好的基网络预测噪声标签。基于教师-学生网络的架构通常会对标签进行软化，使学生网络在带噪学习中更加鲁棒［47-51］。Pham等［52］提出了一种元伪标签（Meta Pseudo Labels）算法，将训练数据中疑似噪声样本的数据视为无标签数据进行半监督学习。由于半监督学习的高效性，非常适合引入标签噪声学习中。图3 是元伪标签的算法流程。

图3 元伪标签算法流程Fig.3 Meta pseudo labels algorithm flow

与传统的伪标签一样，元伪标签使用教师网络给无标记的数据生成伪标签，并且用这个伪标签指导学生网络。不同的是，元伪标签会依据学生网络在有标签样本和伪标签样本上的结果不断调整教师网络。该算法的核心在于，学生网络和教师网络之间存在交替的优化过程。下面给出针对标签噪声的元伪标签学习算法流程。

1）学生网络：抽取一部分未标记数据（疑似噪声数据）xu，利用教师网络的预测值给定伪标签T(xu；θT)，然后使用一步梯度下降更新模型参数。学生网络梯度更新公式为：

2）教师网络：抽取一部分有标记数据（干净数据）(xl，yl)，利用第1）步学生网络优化后的模型参数更新教师网络。教师网络梯度更新公式为：

标签重修正方法从数据本身出发，将噪声标签修正为接近真实类别的标签，能够从根源上提高数据集的质量；但是这种方法十分依赖原本的干净数据集，并且标签重修正的错误可能会容易累加。

2.2 基于损失函数的标签噪声算法

大量研究表明，损失函数的处理会提高标签噪声在训练时的鲁棒性［53］。基于损失函数的标签噪声学习算法主要考虑标签转移矩阵和风险最小化方案的稳健性。前者的目标是估计标签转移矩阵，前向或后向地校正每个样本的损失，以减少错误的累计；后者的目标是设计一个损失函数而不需要估计转移矩阵，使有噪声标签和干净数据的情况下的风险最小化模型相同。损失函数的设计分为两个方面：1）单独改进训练样本误差即损失函数；2）向基础损失函数中加入正则化项以增强模型鲁棒性。因此，下面介绍了关于损失的三种方法：损失校正、鲁棒的损失和损失正则化。

2.2.1 损失校正

损失校正首先需要估计标签转移矩阵［54］，即一个类别与另一个类别的错误标签的概率，然后通过修改训练期间的损失函数以提高鲁棒性。前向校正和后向校正是两种基于标签转移矩阵的损失校正方法［44］。前向校正在前向传播中将估计的标签转移矩阵与Softmax 输出相乘以校正每个样本的损失；后向校正采用没有经过损失校正的Softmax 输出估计标签转移矩阵，然后重新训练模型，将估计的转移矩阵和损失值相乘以校正损失。损失校正方法对标签转移矩阵非常敏感，现实中的标签转移矩阵也很难估计。

2.2.2 鲁棒的损失

鲁棒的损失函数和其他方法相比，是一种更简单、通用的鲁棒学习的解决方案。交叉熵损失（Cross Entropy loss，CE）［55］函数是常用于分类的标准损失函数，收敛快但容易拟合噪声，泛化能力较差。Ghosh等［55］证明了对称损失函数可以鲁棒地标记噪声。由此设计原则导出的对称函数如平均绝对误 差（Mean Absolute Error，MAE）［16］和逆交叉熵（Reverse Cross Entropy，RCE）［56］在多分类标签下的实验结果具有很好的鲁棒性，但是在复杂的数据集上欠拟合。为了探讨损失函数如何同时兼并鲁棒性和可学习性，一系列新的损失函数被提出。Zhang等［57］设计了广义交叉熵（Generalized Cross Entropy，GCE）损失函数，它类似于MAE 和CE 的广义混合。受KL（Kullback-Leibler）散度的启发，Wang等［56］结合CE 和RCE 设计了对称交叉熵（Symmetric Cross Entropy，SCE）损失。但是GCE 和SCE 都只在对称损失和CE 之间进行折中，且SCE 对噪声标签仅具有部分鲁棒性。Ma等［58］对损失函数进行简单的归一化规范处理，证明任何损失函数都可以对有噪声的标签产生鲁棒性。但是归一化交叉熵（Normalized Cross Entropy，NCE）损失函数实际上改变了损失函数的形式，失去了原始损失函数的拟合能力，即损失函数的鲁棒性并不会保证优秀的可学习性。因此又提出了主动被动损失（Active Passive Loss，APL）函数，组合两个对称损失，在保证鲁棒性的同时提高了损失函数的可学习性。

以上损失函数都基于CE 进行改进，通过组合多种形式的损失函数实现鲁棒性和可学习性。另一种鲁棒的损失仅从原CE 出发，研究鲁棒的损失函数。为了探讨交叉熵损失函数和其他损失函数是否存在关联，Feng等［59］受泰勒函数启发，基于CE 提出了一种泰勒交叉熵（Taylor Cross Entropy，TCE）损失（Taylor-Loss）。TCE 通过调整超参t间接地调整泰勒级数以逼近CE，能够拟合训练标签，对标签噪声具有鲁棒性。TCE 不仅继承了CE 的优点，还避免了CE 过拟合的缺点，对标签噪声的鲁棒性更好。TCE 的表达公式为：

Amid等［60］提出CE 在边界和尾部存在固有的两个缺陷：1）逻辑损失是最后一层的激活值的凸函数，远离分类边界的异常值会左右总的损失值；2）Softmax 函数在给类分配概率时，逻辑函数的尾部呈指数衰减，错误的标签会使逻辑函数的尾部呈指数下降，导致处理有噪声数据的泛化能力差。因此，基于Bregman 散度［61］提出了一种双温逻辑损失（Bi-Tempered logistic Loss，BT-Loss），并引入了两个参数：温度t1和尾部重量t2，以约束逻辑损失函数的界限，降低逻辑函数尾部的衰减速度，如式（12）、（13）所示。

以上损失函数都显示了对标签噪声的抗噪性，但是改进损失函数时都引入了超参数，很难一次性确定模型在超参数为何值时训练性能最好。应该继续探索是否存在不包含任何超参数的鲁棒损失函数。

2.2.3 损失正则化

基于损失的正则化技术可以缓解模型过度匹配有噪声标签。与鲁棒损失不同，它通过向基础损失函数中加入正则化项以增强模型的鲁棒性。Zhou等［62］在Softmax 部分增加温度函数锐化网络的输出，采用稀疏正则化（Sparse Regularization，SR）使网络输出稀疏，获得了足够的鲁棒性和学习充分性。SR 的表达公式为：

对抗训练（Adersarial Training，AT）［63-68］以及虚拟对抗训练（Virtual Adersarial Training，VAT）［69］也可以作为正则化方法，以增强机器学习模型的鲁棒性。Szegedy等［70］通过给原始样本构造噪声以生成噪声样本，导致神经网络模型输出错误的分类结果，这些样本就是对抗样本，此过程称为对抗攻击。对抗训练主要发生在构造对抗样本时，会轻微降低深度学习模型预测的准确性。这是一种可接受的权衡，因为它增强了抗对抗性攻击的稳定性。在许多对抗性的例子上微调神经网络会使它在面临对抗攻击时更加稳健。

对抗训练的公式如下：

其中：θ为模型参数；D为数据分布；Ω为扰动空间；L为损失函数；E 为整个数据分布D的损失函数期望。

考虑泰勒展开近似，正则化形式的对抗训练公式为：

添加扰动后的对抗训练公式为：

因此对抗训练可以视为在损失函数上加入正则化项，基于损失函数进行模型的正则化。常用的对抗样本生成策略有快速梯度符号法（Fast Gradient Sign Method，FGSM）［63］、Deepfool［71］、C&W（Carlini and Wagner attacks）［72］等。

虚拟对抗训练是另一种有效的基于损失正则化的技术［69］，它加入微小扰动以生成特定的数据点，使这些数据点在原始特征空间中非常接近，但在表征向量的空间中却相距较远，然后再训练模型使它们的输出彼此接近。

2.3 基于模型的标签噪声算法

许多研究对模型架构进行了修改，建模了噪声数据集的标签转换矩阵。对模型架构的改变方式包括在Softmax 层上添加一个噪声适配层，或设计一个新的专用架构，以及在不改变模型参数的前提下对模型进行正则化处理。

2.3.1 鲁棒的结构设计

许多研究针对不同的噪声类型修改模型架构，并增加一个额外的噪声层来学习噪声分布，这个噪声分布为噪声层的权重矩阵。是噪声标签的分布，p(y*=i|x，θ)是基本模型的概率输出，那么样本x被预测为标签噪声的概率为：

当训练标签干净时，将噪声层的权重矩阵设置单位矩阵，即没有噪声层。学习目标是在N个样本上最大化对数似然性。可用公式表示为：

处理标签噪声常见的简单方法是在数据预处理阶段对标签噪声进行移除或者纠正［73］。这种方法虽然直接，但是难以区分信息丰富的难样本和错误标签样本［74］。为了克服这个缺陷，研究者们关注深度网络的鲁棒性，而不是数据清理方法，通过修改模型架构，以提升深度网络在噪声标记的多分类的大规模数据集上的鲁棒性。

Sukhbaatar等［75］基于卷积神经网络（Conv.net）提出自底向上（bottom-up）和自顶向下（top-down）两种噪声模型。bottom-up 噪声模型在Softmax 和负对数似然（Negative Log-Likelihood，NLL）cost 层间添加了一个噪声层；top-down 噪声模型在Softmax 和NLL cost 层之后添加了一个噪声层。利用这两个模型能够可靠地从数据中学习噪声分布，显著地提高深度网络的性能。Goldberger等［76］使用附加的Softmax 层来模拟期望最大化（Expectation-Maximum，EM）算法优化的似然函数，提高了模型的普适性，应用EM 算法寻找网络和噪声的参数，并估计正确的标签。迭代期望（Expectation，E）步估计正确的标签，极大（Maximum，M）步对网络反向传播。但是每次预测标签之后都要重新训练模型。

噪声适配层与损失校正方法相似，主要区别在于标签转移矩阵的学习和模型的学习不分开。通过噪声适配层来学习噪声分布需要对噪声类型建立强假设，这限制了模型学习复杂的标签噪声的能力。而基于EM 的模型修改方法容易陷入局部最优，并且计算代价大。为了解决上述问题，新的专用模型架构被提出以处理复杂的标签噪声。Jiang等［77］设计了一个新的噪声模型网络（Noise Modeling Network，NMN）学习噪声转移矩阵，然后使用另一个网络来拟合真实标签的后验概率，计算出来的监督信息可以优化两个子网络。Han等［78］用人类的知识当先验，利用人类对无效的标签转换的认知约束噪声建模过程。因为约束噪声建模需要很强的先验知识，因此采用生成对抗网络（Generative Adversarial Network，GAN）［79］的变体来估计生成模型。

设计的新的专用架构对真实的噪声数据集具备更好的鲁棒性，与噪声适配层相比，对复杂的标签噪声具有更好的抗噪性，但是由于人工设计的特性，不具备噪声适配层的可扩展性。

2.3.2 模型正则化

带有标签噪声的数据集训练模型容易导致模型性能下降，出现过拟合现象。在不改变模型参数量的前提下，对模型进行正则化处理，能够有效提高模型的泛化能力，抑制过拟合。

Li等［80］提出一 种噪声 容忍训 练算法（Meta-Learning based on Noise-Tolerance，MLNT），在传统的梯度更新前先进行元学习更新。在元训练阶段，通过生成的合成噪声标签模拟真实训练，对每一组合成的噪声标签使用梯度下降来更新网络参数；在元测试阶段，尽量使更新后的网络与教师模型给出一致的预测，并训练原始参数使一致性损失总和最小。

Dropout 也是广泛使用的正则化技术。Jindal等［81］添加了一个额外的Softmax 层，并对该层应用了Dropout 正则化，认为它提供了更鲁棒的训练，并防止了由于Dropout 的随机性而产生的记忆噪声。

2.4 基于训练方式的标签噪声算法

本节主要通过改变模型的训练方法，在标签噪声模型中引入半监督方法，从而有效缓解噪声标签对模型分类的影响。本节将分成两部分进行阐述：1）Self-training 算法，如MentorNet［82］；2）Co-training 算法，如DivideMix［36］。

2.4.1 Self-training

Self-training 算法［83］可以提高模型的鲁棒性，具体流程如图4 所示。首先，利用模型训练有标签的数据集得到一个分类器，该步骤与监督学习的方法基本一致；随后，用训练好的分类器训练无标签数据集，给无标签样本生成伪标签，并将置信度高的无标签样本与它的伪标签一同加入训练集；最后，在新的训练集中重复上述步骤直至满足停止条件得到最终的分类器。

图4 Self-training算法流程Fig.4 Self-training algorithm flow

MentorNet［82］是利用数据驱动来训练基础网络的新方法，主要由两部分组成：1）预定义课程，与Self-training 类似，存在因样本选择偏差引起累积误差的缺点；2）学习仅有标签样本的课程。通过一个模拟测试让MentorNet 不断更新所教授的课程，基础网络使用更新后的模型为模拟测试提供相应的特征。而基于干净验证集的Self-training 方式，在样本不均衡且含噪声的数据集中效果不理想。Ren等［37］提出了在附加干净无偏验证集情况下的标签噪声算法。该算法虽然训练时间大概为原来的3 倍，但是无需过多调参，且能同时处理样本不均衡、标签噪声并存的情况。

2.4.2 Co-training

Self-training 算法解决标签噪声的问题有不错的效果，但容易出现错误累加的情况［84］。和Self-training 算法的训练方式不同，Co-training 算法需要训练两个不同的网络，具体流程如图5 所示。

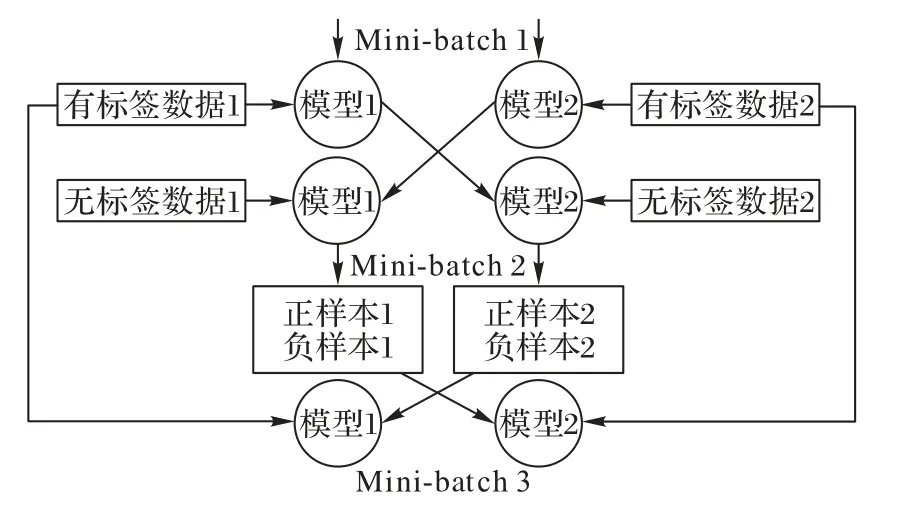
图5 Co-training算法流程Fig.5 Co-training algorithm flow

首先，利用两组不同特征的有标记的样本集分别训练两个分类器，然后将这两个分类器分别训练未标记样本得到两组正样本和负样本；最后，将正负样本加入有标记的样本集，重复上述步骤［84］。

DivideMix 采用高斯混合模型（Gaussian Mixture Model，GMM）判别噪声样本，但存在确认误偏的问题。因此，在Co-Divide 的阶段，每个网络用一个GMM 建模每个样本的损失分布，将数据集分为一个标记集和一个未标记集，随后被用作另一个网络的训练数据进行训练（如图6 所示）。运用两个网络划分数据的性能比利用单个网络的效果更佳［36］。

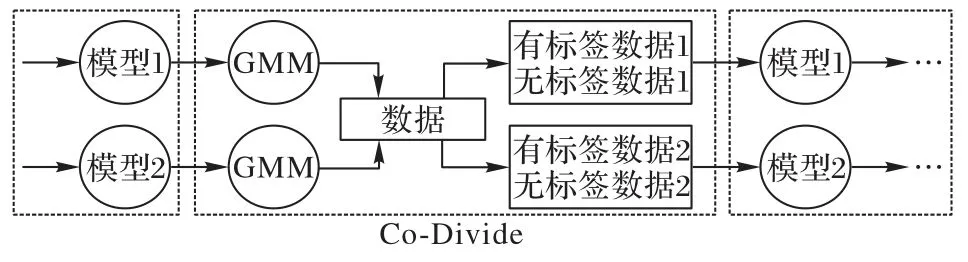
图6 DivideMix算法流程Fig.6 DivideMix algorithm flow

随着训练次数的增加，Co-training 算法在效果上会退化成Self-training 算法中的MentorNet。为解决这一问题，Yu等［85］提出结合分歧更新策略（用！=表示）与联合训练的一种稳健的学习模型Co-Teaching+（如图7 所示）。首先用MentorNet 与Co-Teaching 预测所有数据，但只保留预测结果不相同的样本。在出现分歧的数据中，每个网络选择损失较小的数据用于给另一个模型更新参数。利用“分歧”策略可以保持两个网络的差异，显著提高了联合训练的性能。

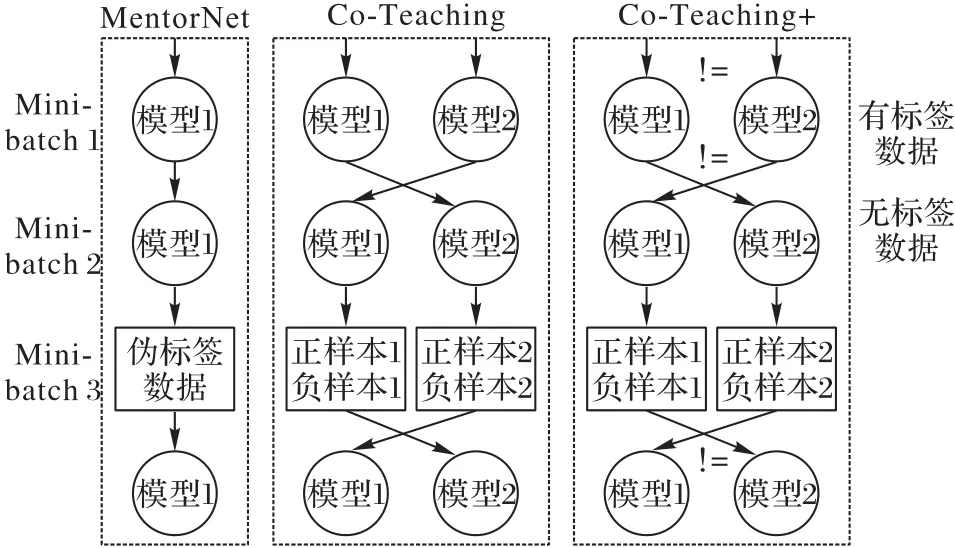
图7 半监督标签噪声算法流程Fig.7 Semi-supervised label noise algorithm flow

引入半监督的训练方式是目前流行的标签噪声算法，显著地提高了对噪声的鲁棒性。虽然这类算法处理标签噪声的效果很好，但是不可避免地会增加大量计算成本。

3 标签噪声数据集及实验对比

3.1 标签噪声常用数据集

通常在CIFAR-10 和CIFAR-100、ImageNet-2012 数据集上进行标签噪声问题的实验对比。

CIFAR-10 数据集是一个用于识别普通物体的小型数据集，一共包含10 个类别的RGB 彩色图片，每个图片的尺寸为32×32，每个类别有6 000 个图像，数据集中一共有50 000 张训练图片和10 000 张测试图片。

CIFAR-100 有100 个类，每个类有600 张大小为32×32 的彩色图像，每类各有500 个训练图像和100 个测试图像。与CIFAR-10 相比，CIFAR-100 数据集更有层次，100 类被分成20 个超类。

CIFAR-10 和CIFAR-100 分别采用对称噪声和非对称噪声两种标签噪声。对称标签噪声通过一个随机的热点向量注入，以r的概率替换样本的真实标签。

使用ImageNet-2012 进行大规模图像分类，该数据集有130 万个图像，有1 000 多个类别的干净标签。

3.2 实验对比分析

表1 为各种算法在添加了不同噪声率r的对称噪声后在CIFAR-10 数据集上的测试准确率对比，其中，噪声率指标签错误的比例。根据文 献［35-36］，CE-Loss、Mixup［86］、Co-Teaching+［85］、Meta-Learning［52］、DivideMix 算法仅提供20%、50%、80% 噪声下的测试准确率结果；MentorNet 和CleanLab［35］算法仅提供20%、40%、70%噪声下的测试准确率结果。横向对比，随着噪声率的提高，各算法的测试准确率都出现了下降趋势，反映了不同算法对标签噪声的抗噪性。纵向对比，不同算法之间的提升较大，引入半监督学习方法的标签噪声算法取得了较大的突破。DivideMix 在所有噪声率下准确率都取得了最优，并且在80%的高对称噪声下，仍能保持0.932 的准确率。

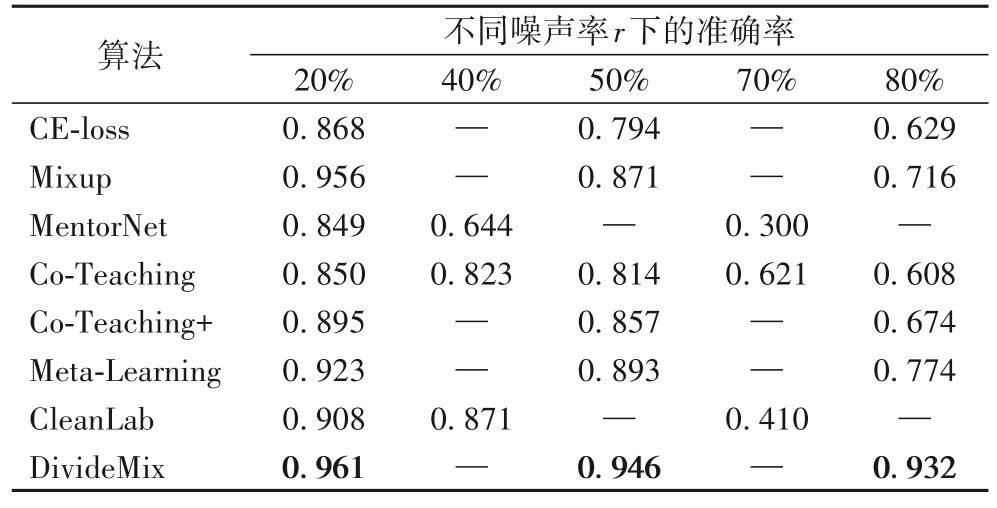
表1 在不同噪声率下CIFAR-10上的测试准确率比较Tab.1 Comparisons of test accuracy on CIFAR-10 under diferrent noise ratios

表2 为在ImageNet-2012 测试集上的Top1 和Top5 准确率，其中，基于模型的标签噪声算法［75］仅提供在不同噪声率下的Top5 准确率。可以看出，鲁棒结构由于人工设计的结构的特性，相较于其他先进方法，准确率较低。在具有不同类型标签噪声的所有数据集上，DivideMix 始终优于对比方法。

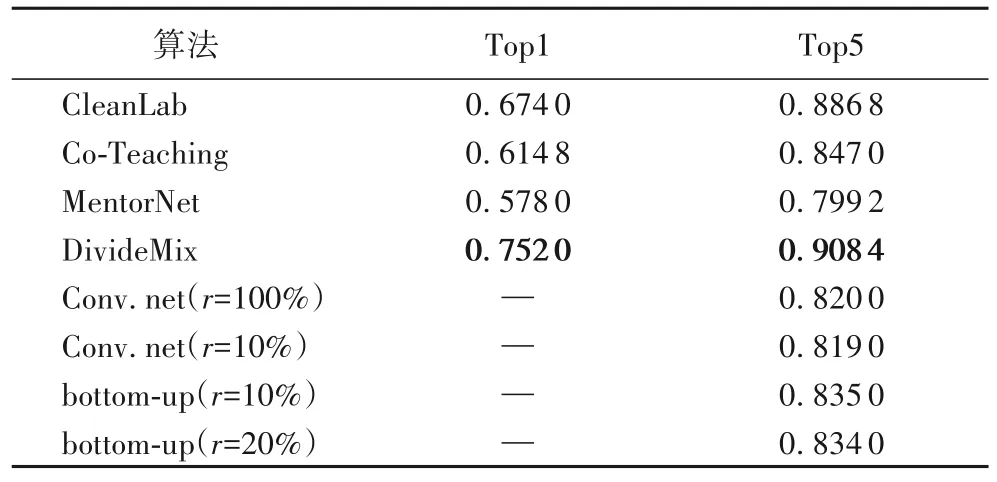
表2 在ImageNet-2012测试集上的Top1和Top5准确率Tab.2 Top1 and Top5 accuracies on ImageNet-2012 test set

表3 是在具有对称标签噪声的CIFAR-100 数据集上的测试准确率，噪声率r=｛20%，40%，50%，60%，80%，90%｝。其中，Taylor-Loss取t=2；BT-Loss的t1和t2分别为0.8、1.2。可以看出，对于具有高噪声率的更具挑战性的CIFAR-100 数据集，以半监督方法为代表的DivideMix 在所有噪声率下准确率仍然远远优于其他方法，且在高噪声率下体现了一定的鲁棒性。纵向对比分析基于损失的标签噪声算法，可以发现近期损失函数的研究取得了重大突破，通过改进损失函数以提高对标签噪声的鲁棒性，相较于其他方法，是一种更简单、更通用的鲁棒学习的解决方案。尤其是BT-Loss 的出色表现，能够与基于训练方式的标签噪声算法抗衡。

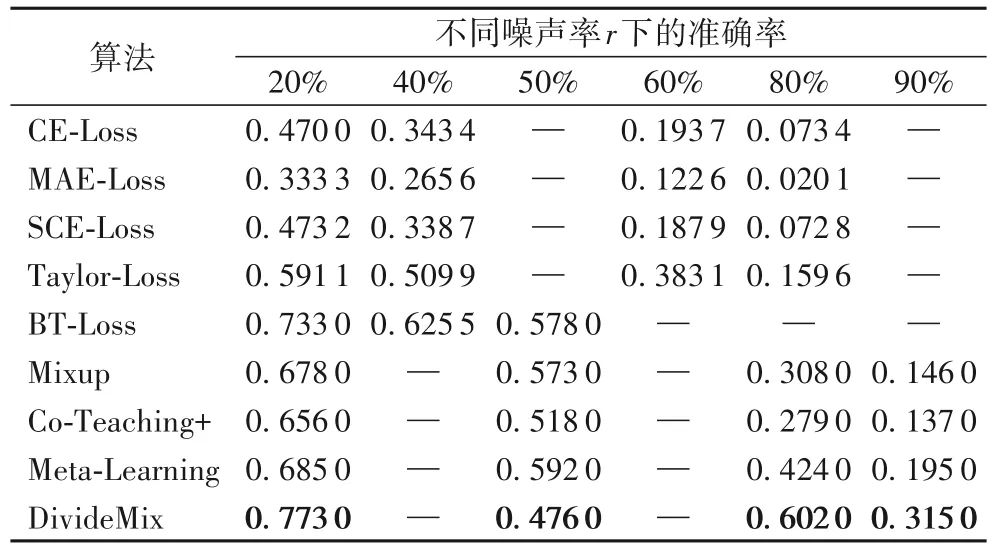
表3 在不同噪声率下CIFAR-100上的测试准确率比较Tab.3 Comparisons of test accuracy on CIFAR-100 under diferrent noise ratios

综上所述，基于损失函数的算法近年来经过不断的研究，突破了同时达到鲁棒学习和可学习性的瓶颈，作为一种简单且通用的鲁棒学习方式取得了明显进步；基于模型的算法通过改变模型架构显著地提高了泛化性能，存在强烈的人工设计特性，它的改进不容易扩展到其他模型架构中；基于训练方式的算法设计了对噪声标签更鲁棒的自适应训练策略，引入半监督学习取得了目前最好的性能，但是这种方法依赖于对学习过程进行干预和调整，或对训练时间和学习速度等超参数敏感，所以很难调节；最后，基于数据的算法能够提高原始标签的质量，但可能会将错误标签校正为正确的标签，可以结合现有的先进算法进一步改进，但是这些方法需要额外的干净数据支持，或者需要一个潜在的昂贵的检测过程来估计噪声模型。

4 基于深度学习的标签噪声处理框架

首先分析存在标签噪声时通用的基于深度学习的标签噪声处理过程，以及算法选择的依据，为处理类似问题提供参考，并比较了本文介绍的四类标签噪声方法，提供了一个算法评价体系。

4.1 标签噪声处理过程

1）评估可否进行标签噪声学习。如果数据量过小并且存在一定程度的标签噪声，为了保证算法的有效性，通常建议继续采集数据后再进行学习。

2）利用弱正则化的模型进行初步训练，观察标签噪声量的大小。由于标签噪声算法的鲁棒设置，如果处理干净数据集，通常会带来一定的精度下降，这时首先应该使用仅能处理轻微噪声的温和的标签噪声算法，即不会在无噪声时导致特别大的精度下降，之后使用CleanLab 等工具进行噪声量的评估。

3）根据标签噪声量的大小进一步选择适合的标签噪声算法。不同噪声量适用的算法不同，因此需要根据预估的噪声量大小为算法选择提供依据。

4）最后衡量学习任务的难易再考虑进一步设计。过度的鲁棒约束会带来模型复杂度的限制，因此需要根据现有模型在数据集上的表现尽可能衡量任务的难易程度。如果任务简单，可以采取更激进的样本筛选等方式；如果任务复杂，需要仔细区分难样本与标签噪声样本。

4.2 算法选择依据

数据集能否直接进行学习通常要考虑以下几个因素：数据集大小、噪声量大小及学习任务的难易程度。考虑因素不同，在标签噪声学习中优先考虑的模型不同。

4.2.1 数据集大小

当数据集较小时，为保证训练结果的准确性，通常建议继续采集数据，或通过旋转、复制等手段进行数据增强，以扩增样本量。当数据量正常时，则从噪声量大小、学习任务的难易程度考虑签噪声学习。

4.2.2 噪声量大小

大规模噪声标签的存在不仅增大模型复杂度，还大幅降低了模型预测性能。在医学图像分割等任务中，会对模型产生极大影响。不同的标签噪声模型对噪声量大小处理的能力不同。当噪声量大时，可以优先考虑DivideMix、样本重加权、标签修正等基于数据的标签噪声学习算法；当噪声量小时，可以选择半监督模型或基于损失的模型，但不适合采用DivideMix 和直接删除样本的重加权方法。

4.2.3 学习任务难易程度

难样本学习一直是标签噪声学习的难点，训练集中通常包含较多的简单样本和较少的难样本，学习难样本能在一定程度上提高模型的泛化能力。若在模型训练时考虑难样本的学习，可以通过元学习利用干净验证集辅助，或采用基于模型或损失函数的方法，也可以采取一些激进的方法，如样本重加权，甚至是删除样本的方法。

4.3 算法评价体系

本节对第3 章中介绍的4 类标签噪声方法根据以下5 个相关属性进行评价，为未来的研究提供帮助。表4 为4 类标签噪声方法在5 个属性下的对比。

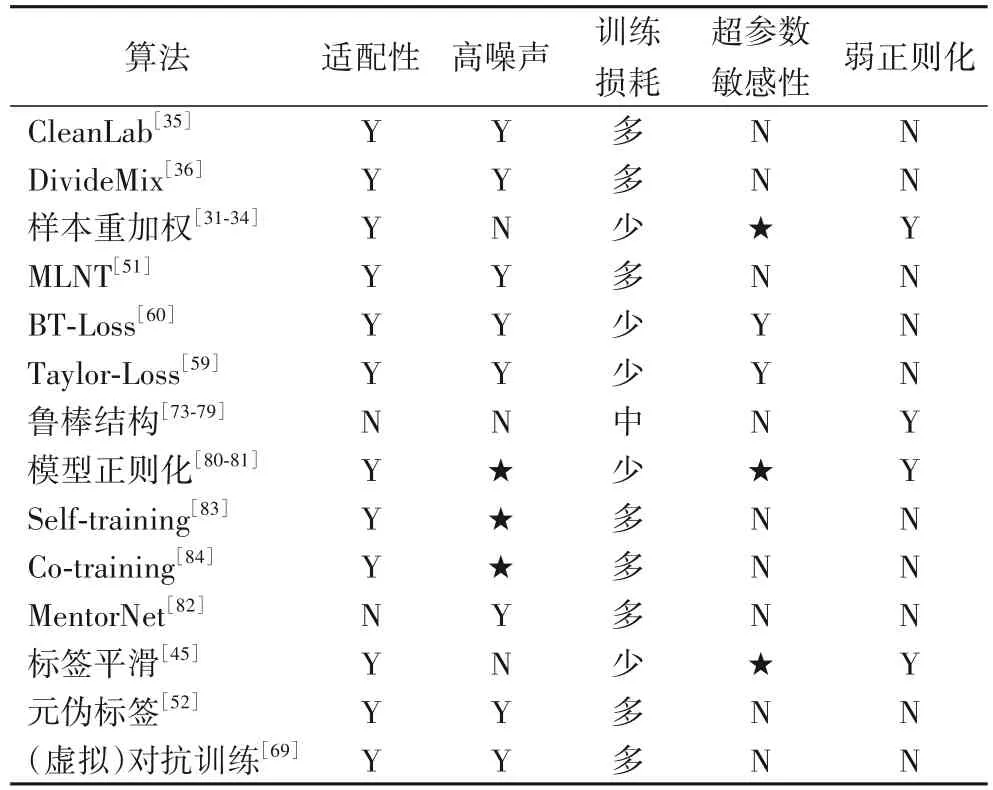
表4 各类算法属性对比Tab.4 Comparison of attributes of various algorithms

1）适配性。随着深度学习的快速发展，一些新的网络结构不断出现并且非常有效；因此，支持任何类型网络结构的能力很重要。适配性能确保标签噪声算法快速适应最先进的网络体系结构。标签噪声算法中的鲁棒损失能很好地与任何网络结构结合，从而提高网络性能，使网络结构能够在不同的标签噪声下保持鲁棒性。

2）高噪声。在真实世界的噪声数据中，噪声率存在从轻到重不同比重的分布；因此，标签噪声算法应对不同程度的噪声率体现出噪声鲁棒性。高噪声确保标签噪声算法甚至可以对抗强噪声。DivideMix 在所有噪声率下都优于其他方法，且在高噪声下体现了一定的鲁棒性。

3）训练损耗。满足深度学习发展的需求离不开硬件技术的进步，不同的网络结构在训练时，模型参数和输出会占用一定的显存损耗和时间计算量成本。因此，训练损耗应确保标签噪声算法在提高噪声鲁棒性的基础上，不额外增加训练的显存损耗、不给学习过程带来额外的计算成本，并保持算法的速率和效率。基于训练的方法大多使用预训练的网络，这会给学习过程带来额外的计算成本。

4）超参数敏感性。深度学习中的超参数指控制训练过程的一些参数，敏感的超参数的不同取值对模型性能的影响很大，找到最好的超参数对模型十分重要。因此，标签噪声算法应衡量对不同取值的超参数的敏感性。鲁棒损失中的BT Loss的t1、t2的不同取值会影响模型对标签噪声的鲁棒性。

5）弱正则化。仅能处理轻微噪声的温和的标签噪声算法，在干净标签情况下反而会导致性能下降，但不会在无噪声情况下带来特别大的精度下降。因此，这种温和的标签噪声算法体现了一种弱正则化。弱正则化确保标签噪声算法在存在轻微噪声的情况下，能够带来性能的提升。基于鲁棒结构的标签噪声算法对中小型数据集的标签噪声具有一定的鲁棒性，但是仅能轻微改善噪声的抑制结果，在干净标签情况下的性能反而略低于真实世界的轻微噪声下的性能。

5 结语

标签噪声存在于真实数据集中，导致深度学习模型难以获得理想的性能；除了图像分类以外，标签噪声还可能存在于所有的有监督学习任务中，例如语义分割、目标检测、文本分类等。本文归纳了大量克服噪声标签现象的标签噪声学习算法，所有的方法都有优缺点及适用性，所以研究者可以为特定场景选择最合适的算法。

尽管目前已经提出了许多标签噪声算法，但在有噪声标签的情况下进行深度学习仍然存在许多问题。考虑到标签噪声对神经网络的影响及分析，例如噪声标签会降低学习效果，尤其是对于具有挑战性的样本；因此，与其说对噪声样本过度适应，不如说对具有挑战性的样本适应不足可能是模型性能下降的原因，这是一个有待解决的问题。另一个可能的研究方向可能是努力打破噪声的结构，使它在特征域中均匀分布。