用等效双星方法求解弹簧双振子问题——以2022年全国高考乙卷理综第25题为例

彭定辉

(江西省南丰县第一中学，江西 抚州 344500)

1 问题引入

弹簧双振子是指两物块与弹簧相连构成二体系统，在系统质心做变速或匀速直线运动的同时，两物块相对质心做简谐运动．[1]弹簧双振子模型在物理竞赛中出现频次较高，偶尔也出现于高考题中，如2022年全国高考乙卷理综第25题，原题如下.

如图1(a)，一质量为m的物块A与轻质弹簧连接，静止在光滑水平面上；物块B向A运动，t=0时与弹簧接触，到t=2t0时与弹簧分离，第1次碰撞结束，A、B的v-t图像如图1(b)所示．已知从t=0到t=t0时间内，物块A运动的距离为0.36v0t0．A、B分离后，A滑上粗糙斜面，然后滑下，与一直在水平面上运动的B再次碰撞．之后A再次滑上斜面，达到的最高点与前一次相同．斜面倾角θ(sinθ=0.6)，与水平面光滑连接．碰撞过程中弹簧始终处于弹性限度内．求

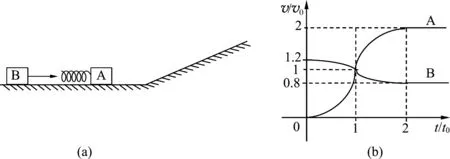
图1

(1) 第1次碰撞过程中，弹簧弹性势能的最大值；

(2) 第1次碰撞过程中，弹簧压缩量的最大值；

(3) 物块A与斜面间的动摩擦因数．

该题是一道典型的力学综合题，涉及动量、能量和牛顿运动定律等核心知识，其运动过程较为复杂，分析起来有一定的难度．特别是该题第(2)问，常规做法是用微元法结合动量定理处理，但这种处理方案必须用到题设条件0.36v0t0，而且只能对特定位置或特定过程进行求解．为此，本文试图寻找一种简易方法，可在中学物理范围内严格求解弹簧双振子任意时刻的物理状态．

2 运动分析

基于高考题情景，将物块从弹簧原长位置开始压缩到恢复弹簧原长的运动称为一次挤压过程．考虑系统不受其他外力的一般情况，对挤压过程进行分析．设弹簧原长为l0，劲度系数为k，两物块A、B的质量分别为m、M，在地面坐标系中位置。

分别为xA、xB．

根据牛顿第二定律，有

(1)

(2)

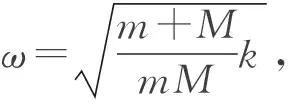
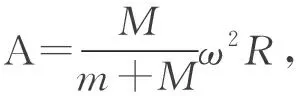
对两式积分，可得两物块的速度为

再次积分，可得两物块的位移为

将前面两式代入(1)式，有C=C′，D=D′+l0．

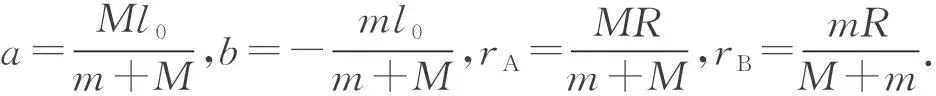
故挤压过程中两物块的位移为

xA=x0+a+v0t-rAsin(ωt).

(3)

xB=x0+b+v0t+rBsin(ωt).

(4)

两物块的速度为

vA=v0-ωrAcos(ωt).

(5)

vB=v0+ωrBcos(ωt).

(6)

不难看出，当cos(ωt)=0时两物块有共同速度且等于质心速度v0．

将t=0代入(5)(6)两式，得vA0=v0-ωrA，vB0=v0+ωrB．当弹簧恢复原长时，由(3)(4)两式有ωt=π，代入(5)(6)两式，得两物块的末速度为vAt=v0+ωrA，vBt=v0-ωrB．联立各式，得

即系统质心速度亦等于挤压过程两物块初、末速度的平均值．

3 等效双星方法

选取质心参考系，通过x′=x-(x0+v0t)变换位置坐标，可得质心系中两物块的位移方程为

xA′=a-rAsin(ωt).

(7)

xB′=b+rBsin(ωt).

(8)

从方程可知，质心系中两物块在各自平衡位置附近做同频反相的简谐运动.

由于简谐运动可等效为匀速圆周运动(参考圆)投影的分运动，[3]那么质心系中弹簧双振子的两个简谐运动亦可拓展为两个匀速圆周运动.故对物块A，在y方向构建一个同频同幅的简谐运动yA′=-rAcos(ωt)，使之与原x方向的简谐运动xA′=a-rAsin(ωt)合成，所得圆周运动轨迹方程为

(xA′-a)2+yA′2=rA2.

对物块B，同样构建简谐运动yB′=rBcos(ωt)，使之与原x方向的简谐运动xB′=b+rBsin(ωt)合成，所得圆周运动轨迹方程为

(xB′-b)2+yB′2=rB2.

显然，两圆圆心位置为两物块的平衡位置，距离为弹簧原长，即a-b=l0；轨道半径等于两物块做简谐运动的振幅；速度大小等于两物块振动的最大速度，有uA=ωrA，uB=ωrB．

发现两个圆周运动的力学规律与天体运动的双星系统[4]十分相似，同样存在mrA=MrB、muA=MuB、mω2rA=Mω2rB等约束关系．由(7)(8)两式作出质心系中弹簧双振子的简谐运动与两个圆周运动的对应投影图像如图2，若平移两圆使圆心重合，则所得图像与双星系统的轨迹相同．因此将质心系中弹簧双振子对应的两个圆周运动称为等效双星．

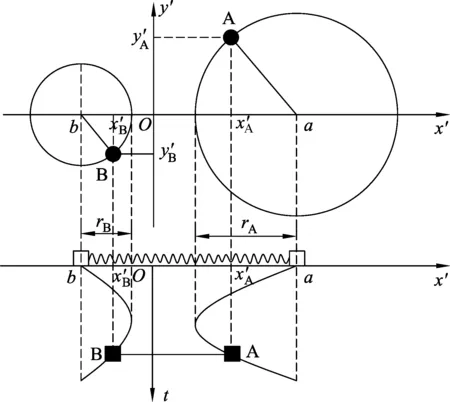
图2 弹簧双振子与圆周运动的投影对应关系

此外，将等效双星的速度矢量平移到同一个位置，则两速度矢量随时间变化的轨迹亦如双星系统图像，其在x方向的投影与由(5)(6)两式的速度图像对应，如图3所示.

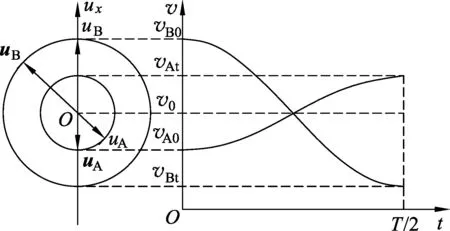
图3 弹簧双振子的速度图像与圆周运动速度矢量的投影对应关系

从图3中容易看出，两图线交点位置对应于系统的质心速度，而两物块的速度图像相对交点位置对称，即有

uA=vAt-v0=v0-vA0，

uB=vB0-v0=v0-vBt.

等效双星之于弹簧双振子，犹如参考圆之于简谐运动，无需求解微积分方程，仅由等效双星的矢量投影对应，便可严格求得弹簧双振子在任意时刻的位置和速度．

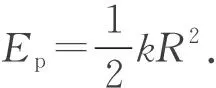
即弹簧双振子的最大弹性势能等于等效双星的总动能．

4 问题求解

下面用等效双星方法对2022年全国高考乙卷的第25题进行求解．

(1) 从图1(b)知0到2t0时间为弹簧双振子系统的第1次挤压过程，其质心速度为v0．故双星圆周运动速度大小分别为uA=v0-0=v0、uB=1.2v0-v0=0.2v0．由muA=MuB，可得M=5m．而弹簧双振子的最大弹性势能等于双星圆周运动的总动能，即

(3) A从斜面返回后与B第2次挤压弹簧，设此过程系统质心速度为vc，作出第2次挤压过程的弹簧双振子的速度图像，如图4所示．

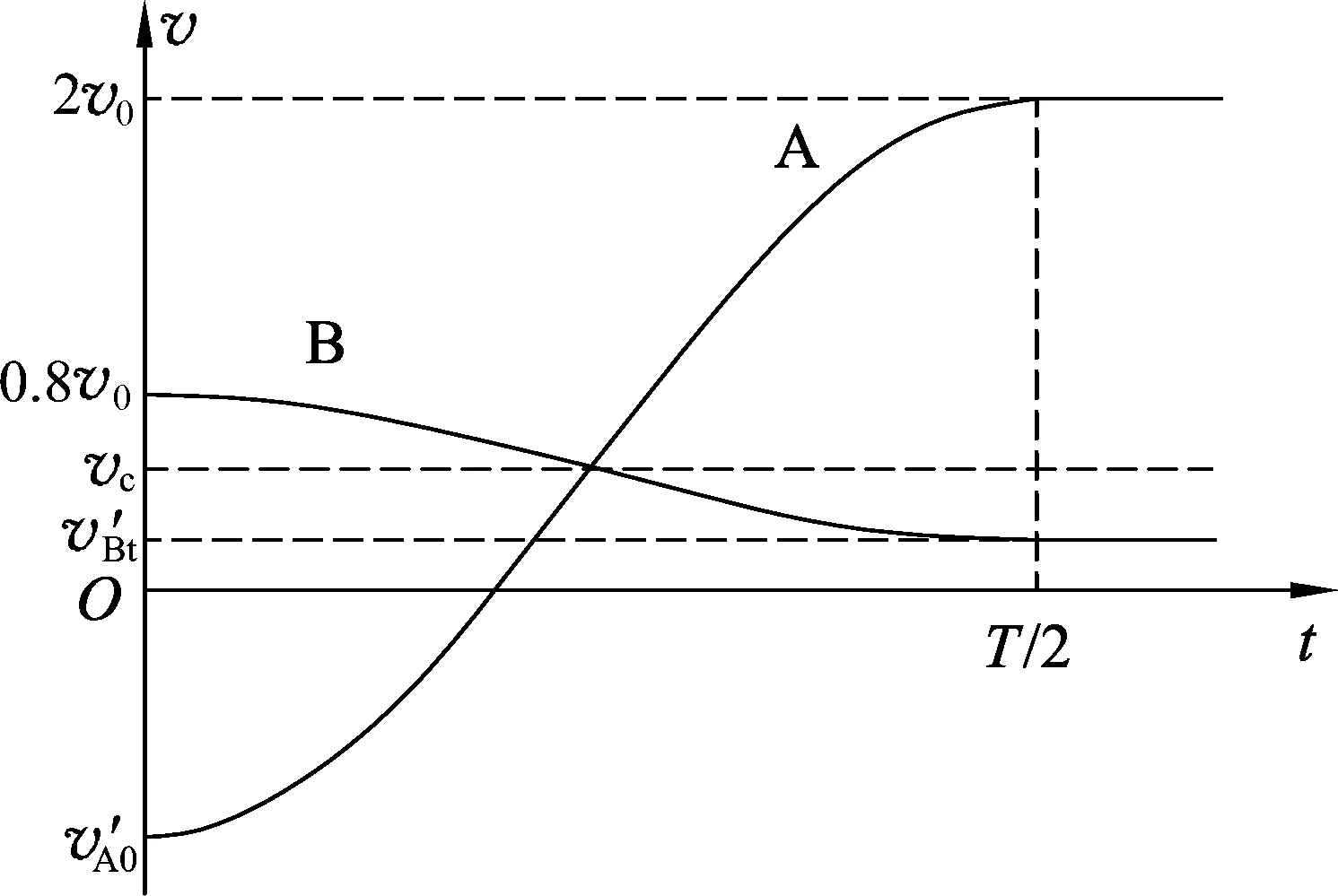
图4 第2次挤压过程中弹簧双振子的速度图像

由题意可知，第2次挤压时B的初速度为第1次挤压的末速度，即0.8v0，其对应的圆周运动速度为uB′=0.8v0-vc．而第2次挤压后A能再次滑上与前次相同的高度，则其末速度与前次的末速度相同，即2v0．故A对应的圆周运动速度为uA′=2v0-vc．由muA′=MuB′，解得vc=0.5v0．

设A首次滑上斜面的最大距离为L，由动能定理有

则其下滑时同样有

联立两式求解得

5 结束语

用等效双星方法求解弹簧双振子问题，其计算过程简单直观，仅用到质心参考系和匀速圆周运动知识，比较适合中学物理教学．该方法作为简谐运动参考圆的拓展，可以帮助学生将所学知识运用到陌生场景，有利于培养学生的科学探究能力和物理建模能力．

限于篇幅，本文仅讨论了无外力作用下的弹簧双振子问题，对于有外力作用的情况，等效双星方法仍具有一定的参考价值．