跨学科视角下美英早期教科书三角学的应用

石 城 汪晓勤

(华东师范大学教师教育学院 200062)

1 引言

在全球化的大背景下，社会产生了许多综合性的问题，传统单一的分科教学难以独自应对，因而基础教育需要更加重视创新型人才和复合型人才的培养．《普通高中数学课程标准(2017版2020年修改)》(简称《标准》)强调数学与生活以及其他学科的联系，提升学生应用数学解决实际问题的能力[1]．开展跨学科教学已然成为国际数学课程改革的大趋势．

虽然我国中小学愈发重视学生跨学科素养的发展，然而跨学科教学资源的匮乏仍然是横亘在中小学一线教师面前的一大难题[2]．跨学科教学不仅仅是多个学科知识并置在一起，而是有效整合各个学科之间的知识来解决真实合理的复杂问题情境．

三角学是在实践中产生、发展、完善的学科，不仅有丰富的数学应用价值，更有许多可供开展跨学科教学的丰富素材．在天文学中，早期三角学从属于天文学，通过预测天体的运动路线和位置来报时和历法推算[3]．在物理学中，现代三角学以其几何作图的形象性和算术计算的精准性推动着物理学各分支的进步，在运动学、力学、声学、光学等领域都作出了杰出贡献[4]．

本文从跨学科的角度出发，拟聚焦美英早期三角学教科书中三角学在天文、物理中的应用，以试图回答以下问题：早期教科书呈现了三角学在天文、物理方面有哪些应用？有关应用问题有何特点？对今日的三角学跨学科教学有何启示？

2 早期教科书的选取

艾伦·雷普克在《如何进行跨学科研究》中提出：跨学科是以现实问题的研究和解决为依托，以多个学科为载体，关注复杂问题或课题的全面分析与解决，希望掌握明确、整合的研究方法和思维方式[5]．本文研究以三角学为中心、天文学和物理学为背景的跨学科内容．在详细阅读1800—1958年间出版的美英早期数学教科书的引言和正文部分后，从中选取三角学在天文、物理中的应用作为研究对象，以40年为一个时间段进行划分，109本出版时间分布情况如 图1所示．其中，对于同一作者再版的教科书，若内容无显著变化，则选取最早的版本，若内容有显著变化，则将其视为不同的教科书．

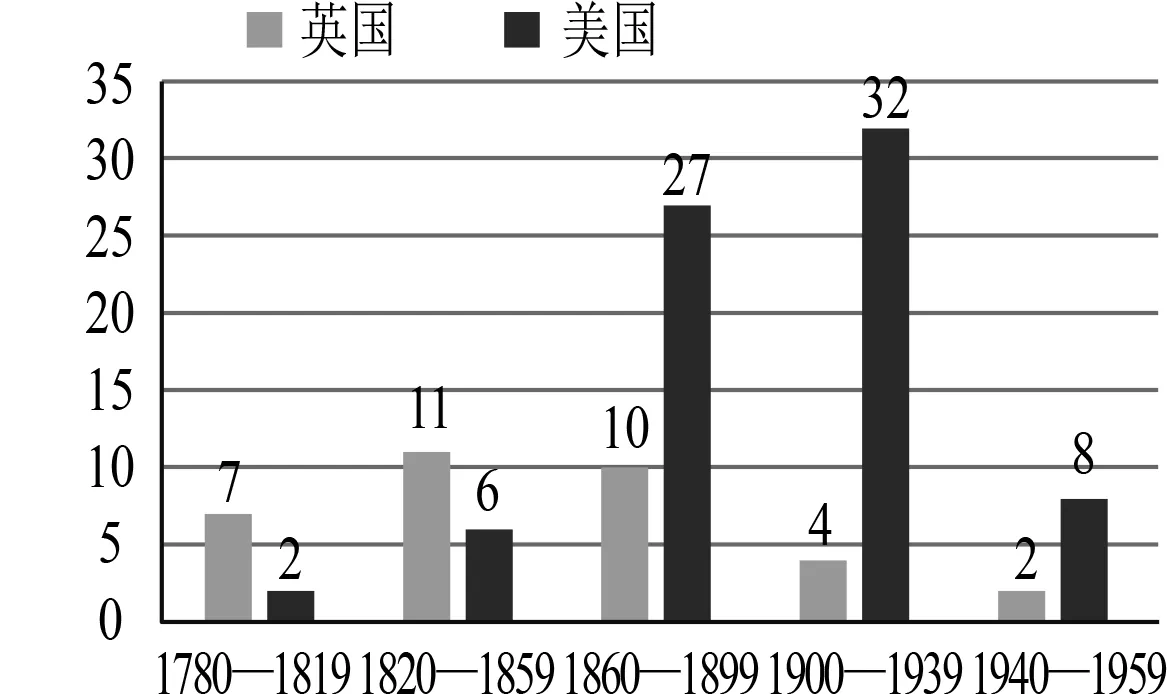
图1 109种教科书的 出版年份和国家分布

三角学在天文方面的应用主要体现在测量天体的大小和天体之间的远近，在物理方面的应用主要体现在运动学和力学，具体问题见表1．

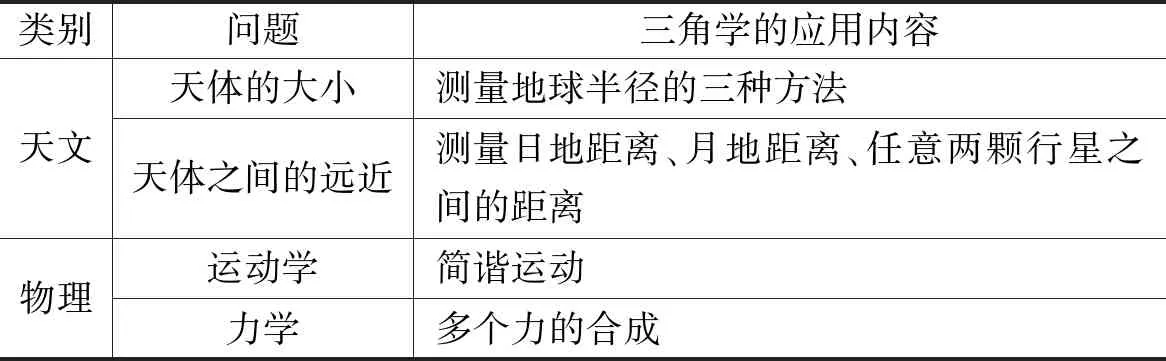
表1 三角学的应用内容及所属类型

3 三角学在天文学中的应用

3.1 计算地球半径的三种方法

(1)弧度测量法

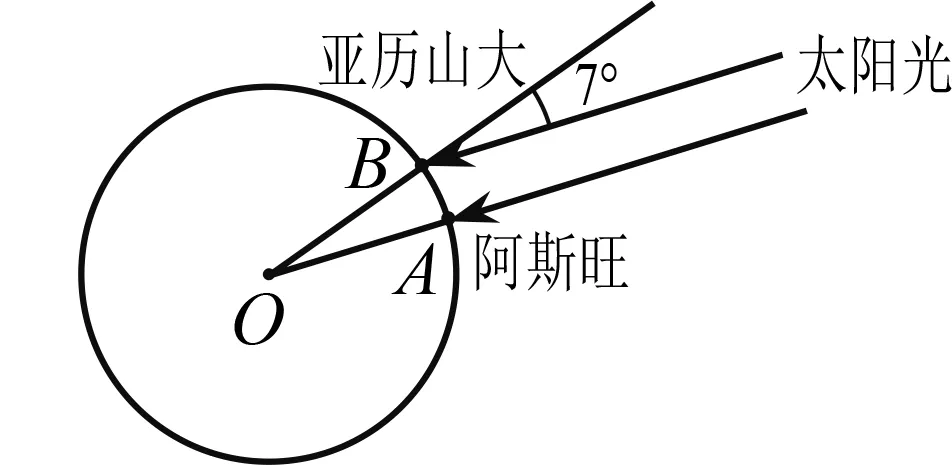
图2 埃拉托色尼 测算地球半径

这种方法是基于假设A,B两地在同一条经线上，并且两地同在北回归线上，才能有夏至日的太阳直射，这与实际情况相差很大．但是在没有精密测量仪器的两千多年前，人们对于地球外面的世界一无所知，这样的发现已经是一个奇迹，充分体现了数学家的智慧．

(2)山顶测量法

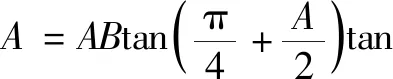
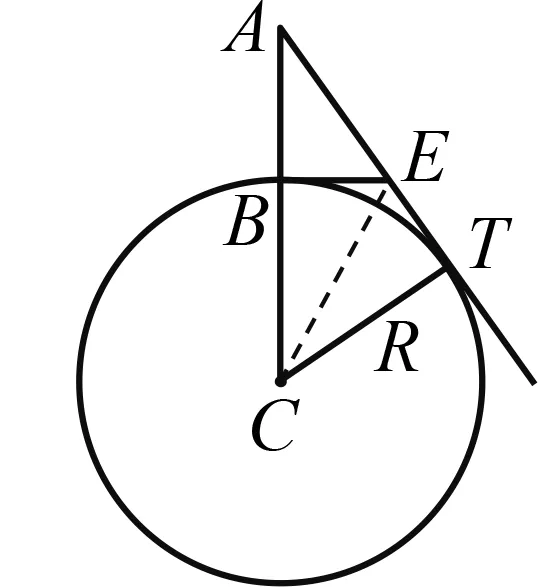
图3 山顶法 测算地球半径

山顶法相较于之前的方法更为准确．通过天体半径可以计算出天体大致的体积和表面积，从而了解天体的大小．

(3)地平俯角测量法

Colenso通过反三角函数和地平俯角(地平线和视线水平线的夹角)表示出了地球半径[9]：如 图4，设地球球心为C，半径为R，两块相距为d的海中巨型礁石分别为A,B，从它们的顶峰F和G测量的地平俯角分别为α和β．

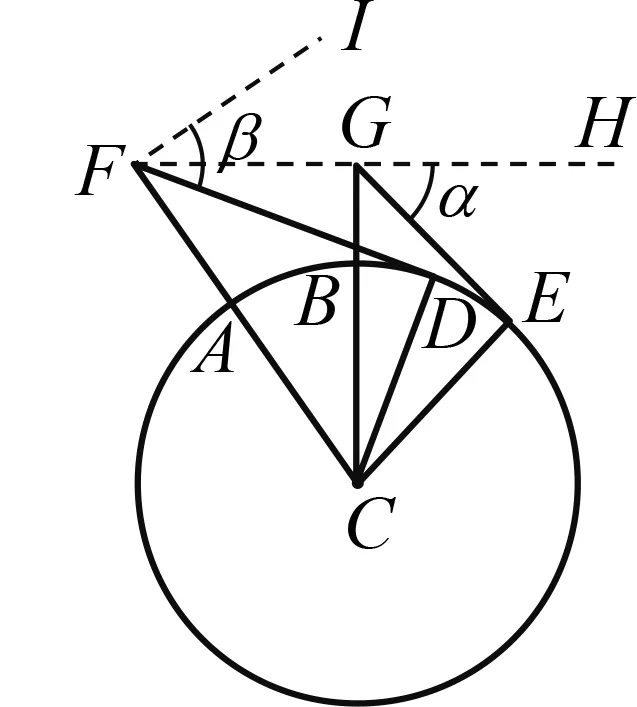
图4 地平俯角 测量地球半径

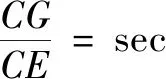
3.2 测量日地距离

如图5，Durell介绍了测量太阳到地球的距离(简称日地距离)的方法[10]：

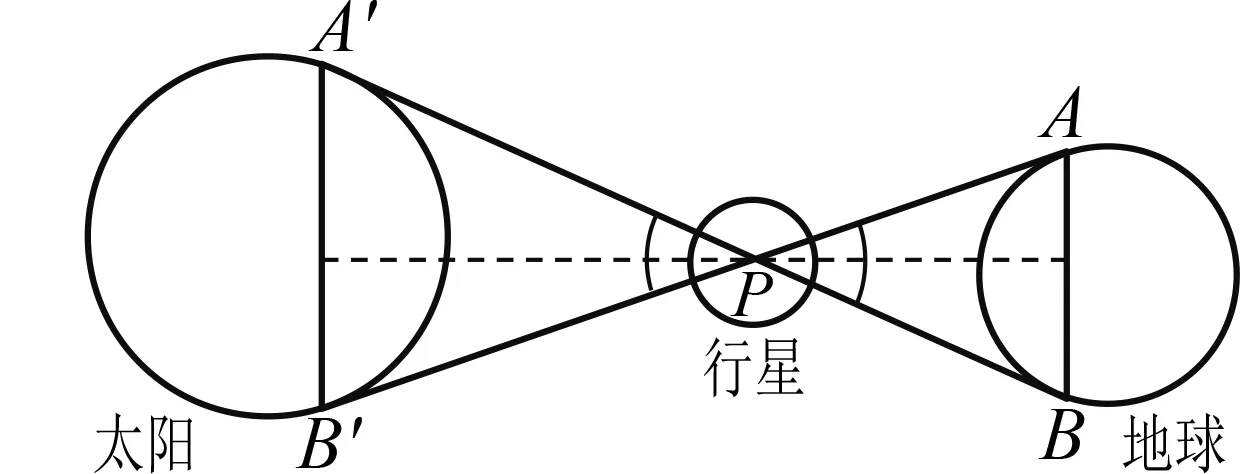
图5 测量日地距离

第一步 先画一条与地球轨道直径大致相等的线段AB作为基准线，确定一个方便观测的行星P的位置，从A,B两点观测P，连结AP,BP，观测∠BAP和∠ABP的度数．已知等腰三角形的底边和两邻角，根据解三角形法则可以求得地球到行星P的距离．

此方法后来被称为“金星凌日法”．

3.3 测量月地距离和月球半径

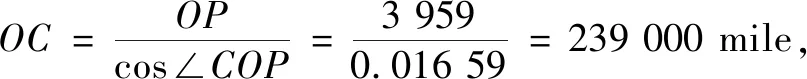
图6 测量月地距离 图7 测量月地半径

事实上，对图6的模型稍加修改，就可以求得月球半径[11]：如图7，设地球半径为EO，月球半径为NM，当已知∠EMO，计算得到月地距离OM后，只需要用同样的方法测量∠NOM，在Rt△NOM中，由MN=OMcos∠EMO可以得到月球的半径．

3.4 测量任意一颗行星到地球距离

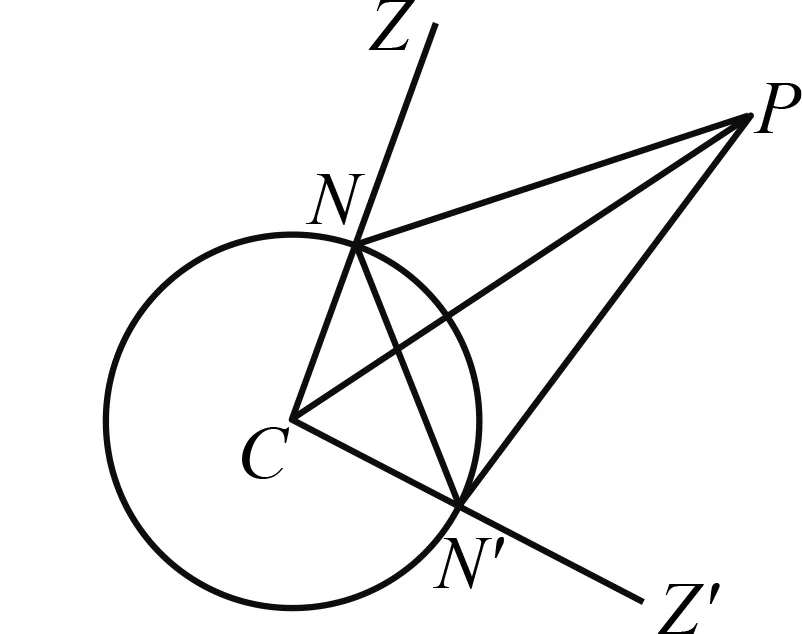
图8 测量行星到地球

4 三角学在物理中的运用

4.1 简谐运动

物理学中存在大量周而复始的运动，如单摆、潮汐、电磁波、音叉振动、交流电等等，而三角函数是刻画周期现象最典型的数学模型，一般周期现象都可以用正余弦函数来表示．

简谐运动是最简单的周期运动，它对研究周期现象起着关键作用．简谐运动可用生活中的简单物品来演示．如图9，一根细绳一端系在振动的音叉上，另一端同钢笔固定在烟色玻璃上．如果玻璃不动，那么钢笔P画出的运动轨迹是一条直线．而如果玻璃匀速向右运动，则P会呈现波浪式的轨迹，这就是简谐运动的轨迹，可以看作是简谐曲线的图象[13]．图10则将细绳一端系在钟摆上，另一端随着钟摆的上下规律摆动在纸上画出简谐曲线y=Asin(ωt+φ)[14]．

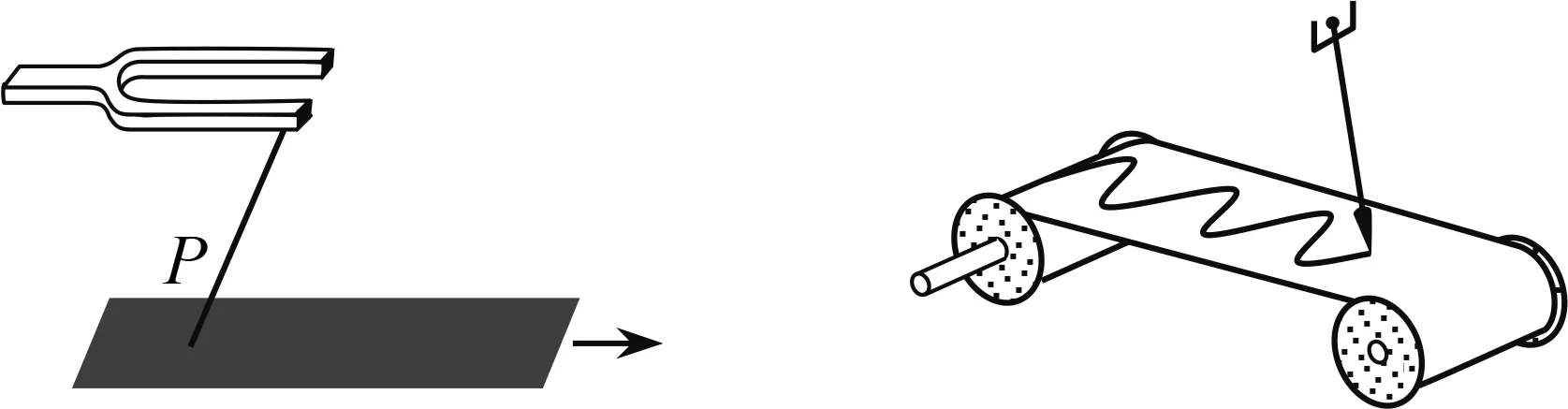
图9 音叉的简谐运动 图10 钟摆的简谐运动

许多不同的简谐曲线可以组成一般谐波曲线．但是反过来，一条给定曲线，如气温计、气压表上的数据画出的曲线，如果有周期性，是否可以认为是若干条简谐曲线合成的呢？该问题的解决过程就是调和分析的主要内容，可以使用三角插值，利用计算数学中的逼近思想来求解,这在基础数学和应用数学领域有着相当重要的地位．

正是这种将任何周期函数用正弦函数和余弦函数构成的无穷级数来表示，将复杂过程看成简单模式叠加的想法，成为了傅里叶级数理论建立的基础，后者在物理的热学、光学、电磁学、声学等领域都有广泛的应用，同时对数学物理这门学科作出了划时代的贡献[15]．

4.2 两个力的合成

对于两个力的合成，根据平行四边形法则，将力AB和AC合成为力AD．因为力是矢量，为了求出合力的大小和方向，需要使用解三角形的相关知识[16]．

(1)平行四边形法则

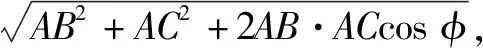
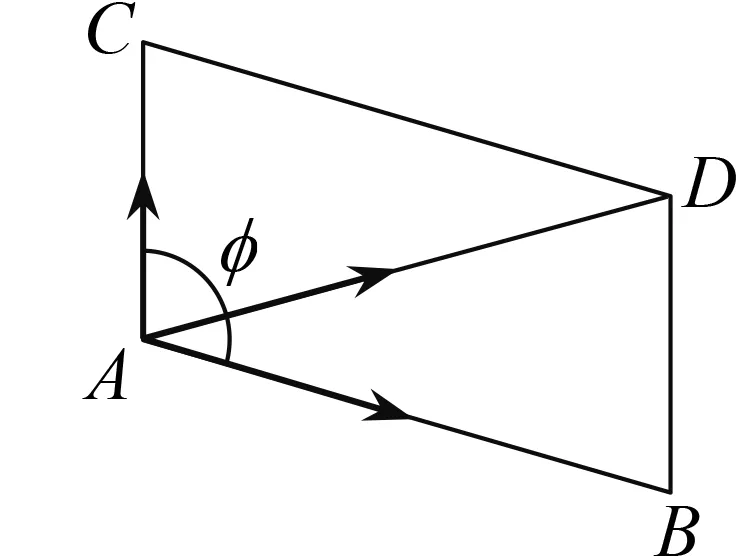
图11 力合成的 平行四边形法则

(2)三角形法则

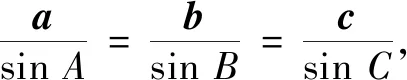
图12 力的合成 三角形法则

4.3 多个力的合成

更为一般的，如果有两个以上力作用于同一点P，那么合力可以按照复数的加法来运算：如图13，假设四个力fi(i=1,2,3,4)作用在P点，ri和θi(i=1,2,3,4)分别表示每个力的大小和方向，则每个力可以用fi=ri(cosθi=isinθi)(i=1,2,3,4)来表示．

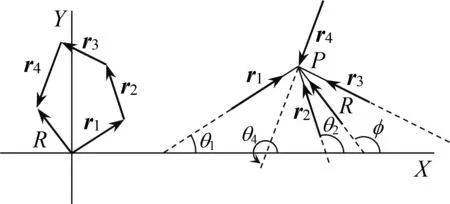
图13 复数加法求合力

按照复数的运算法则，将fi(i=1,2,3,4)的 实部和虚部对应相加得F=r1cosθ1+r2cosθ2+r3cosθ3+r4cosθ4+i(r1sinθ1+r2sinθ2+r3sinθ3+r4sinθ4)=R(cosφ+isinφ)，其中R表示合力的长度，φ表示合力与x轴所成的夹角．引入复数将原来的矢量运算转化为代数运算，不光适用于力学，也适用于运动学中的合运动与分运动，因而在理论物理中发挥着重要作用[17]．

5 教学启示

早期教科书中以三角学为中心的跨学科内容十分丰富，不仅涉及数学的诸多分支，如计算数学、应用数学、代数学和几何学，还涵盖物理、天文等方面的专业知识．这给我们今日的数学教学提供了丰富的素材和宝贵经验．

(1)以素养为导向，用问题驱动教学．跨学科教学的目标是利用知识的迁移促进学科理解，提升学科核心素养．而数学学科核心素养的生成离不开问题解决．三角学是在天文学应用中产生，最终又可以广泛运用到各学科的实践中的学科，这其中产生了大量复杂真实且科学的问题情景．在求解天文学中地球半径问题时，早期三角学教科书呈现出了丰富多彩的方法，这些模型不仅是孕育数学建模和逻辑推理素养的天然摇篮，还是锻炼学生直观想象、数学抽象素养的良好素材．问题是数学的心脏，也是数学课程中跨学科主题学习项目的关键．跨学科主题学习项目中的问题设置，可以以“问题链”为依托，体现数学的工具性，使得学生在问题驱动下更有效地获得知识．以“天文学中测量天体之间的远近”为例，从测量日地距离、月地距离到任意一颗行星到地球的距离，从特殊到一般，层层递进，充分体现问题情境的现实性、复杂性和开放性．

(2)重视学科交叉，培养跨学科思维．数学以严谨的逻辑结构、纯粹的形式公理化体系以及独特的符号语言系统而具有不容置疑的科学性,但是其抽象性使许多人望而却步．日新月异的社会发展使学科之间的交互融合越来越重要，开展以数学为中心的跨学科教学，可以打破学科壁垒，丰富教学内容，开阔学生视野，摆脱数学是被束之高阁的抽象理论的错误观念，让学生认识数学的应用价值、文化价值、科学价值．另一方面，数学的融入使得学生跳出原有的思维束缚,多角度、多方位思考问题．以物理学中力的合成问题为例，数学思想方法的介入为解决多个力的合成问题注入了新的活力．

(3)设计探究活动，理论实践相结合．跨学科教学不是知识的被动接受，而是经验的自主建构[18]．因而以学生为中心的发现式、探究式或建构式学习是开展跨学科教学的抓手．三角学巧妙地联系起了天文、物理和数学，适合开展综合性的数学建模与数学探究活动．从生活中振动的音叉和摇晃的钟摆出发，引导学生发现这种规律性运动的特征，再探究物理学中简谐运动的特性，从而建立其与三角函数的自然联系．这样不仅加深了对物理学中简谐运动的认识，同时也有助于把握三角函数的本质属性——周期性．在课堂教学中可以使用现代化的教育技术，利用VR技术播放教育科普短片，让学生身临其境地体会到三角学在社会生产中发挥的作用．还可以通过角色扮演活动，让学生分角色扮演天文学家和物理学家，运用所学知识解决曾困扰古人数百年的问题，如地球到底有多大、太阳离我们到底有多远等．