探相似之用 寻教学之材*

孔雯晴

(华东师范大学教师教育学院 200062)

在初中的数学课程中，利用相似解决实际问题是培养学生数学应用意识的重要内容．北师大版和沪科版教科书设计了利用影长、标杆和镜面测高的实践活动，人教版教科书中包含影长测高、利用相似测河宽等问题．在已有的教学案例中，泰勒斯的故事已是老生常谈，关于“相似三角形的应用”的教学设计缺乏具有新意的素材．有教师尝试将数学史融入教学[1-3]，获得了学生积极的反馈．因此，本文聚焦相似三角形的实际应用这一主题，考察历史上的相关文献和书籍(包括美国早期教科书)，以期为今天的教学提供更多的素材．

1 测量之术

早在古巴比伦时期，人们就已经知道了两个相似三角形的对应边成比例.事实上，古人是为了解决实际问题才研究几何的，他们对于三角形的认识源自于实际测量的需要[4]．

1.1 用矩之道

我国测量学的历史几乎可以追溯到大禹治水时期，据《史记·夏本纪》记载，在那个工具落后的时代，大禹“左准绳，右规矩”，因势利导，化堵为疏，其三过家门而不入的故事流传至今．大禹所用之“矩”，形似现代的曲尺，它是如何在测量中发挥作用的呢？

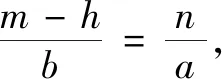
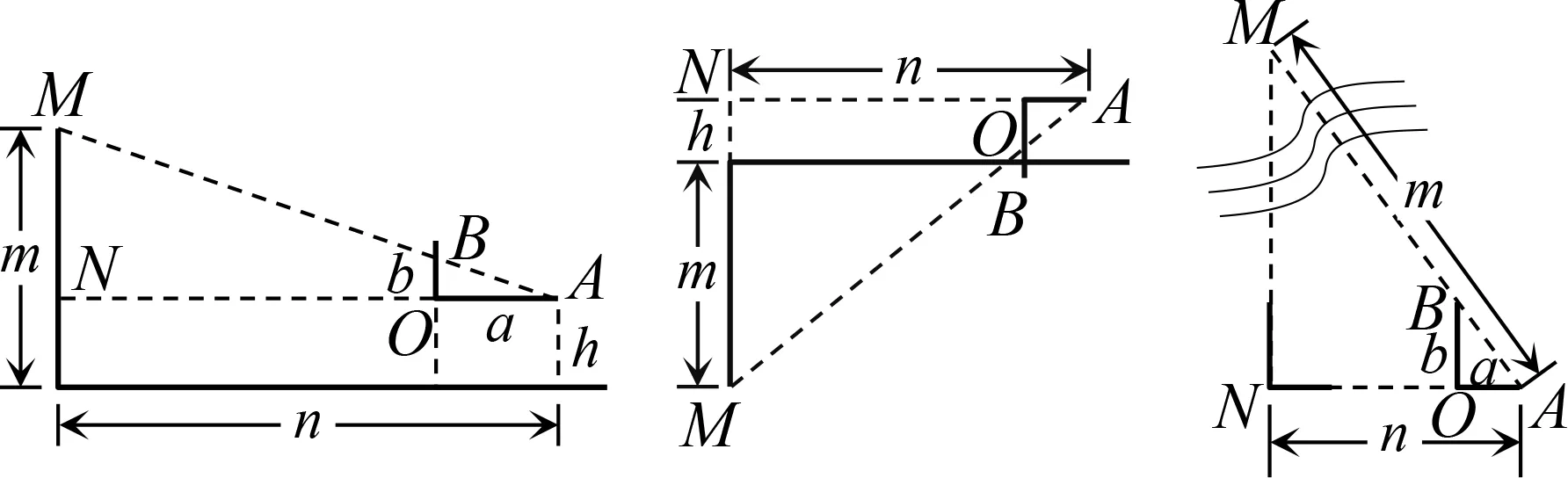
图1 用矩测高 图2 用矩测深 图3 用矩测远

显然，用矩测高需要满足被测物体底部可达的条件.如果情况更复杂一些，有什么解决办法呢？

1.2 重差术

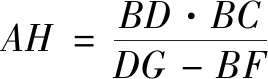
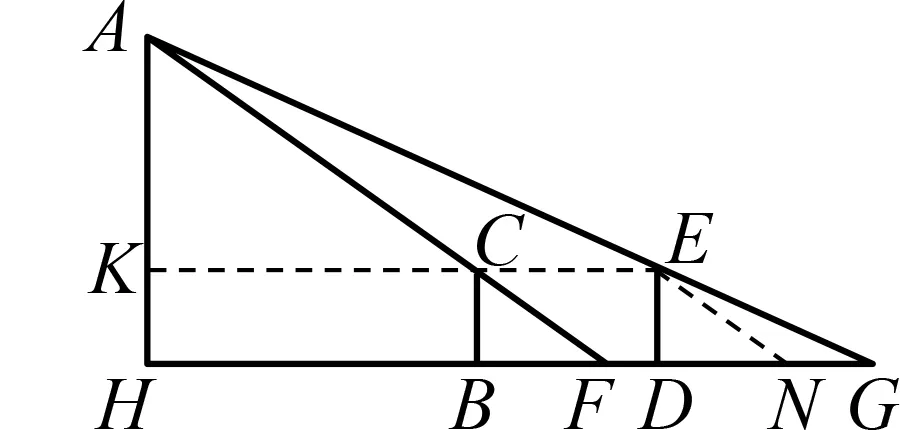
图4 重差术

在《周髀算经》中，陈子用南北两地日影差求 太阳高度的方法就是重差术的雏形[6]，图4中的点A代表太阳，BF和DG分别代表影长．我们知道，地球是一个球体而非平面，所以陈子测日高的方法实际上是没有意义的．若是针对生活中一般的测量问题，地面的弧度可忽略不计，此时重差术是行之有效的[7]．

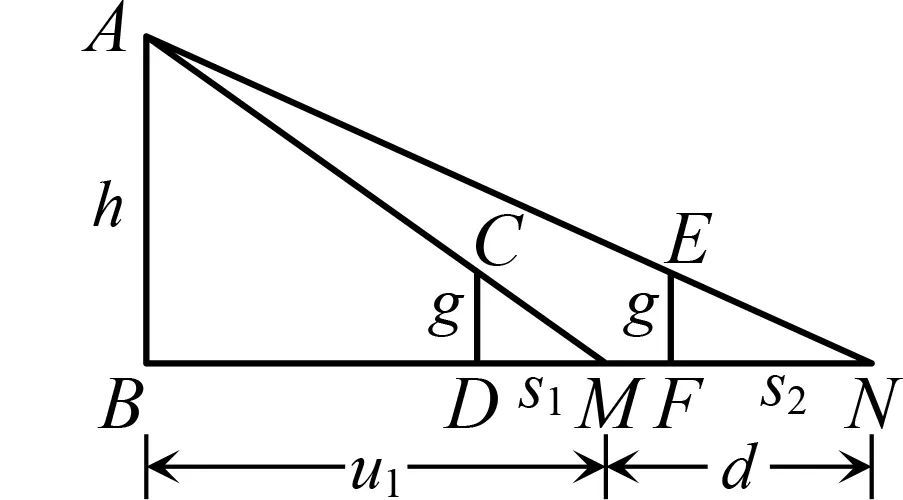
图5 晷尺测高

于12世纪面世的《莉拉沃蒂》是古印度最具影响力的算术著作，书中“关于影之实用算法”一章详细介绍了一系列由灯火而产生的表(标杆)影问题，主要与相似三角形相关[9]．光源和影长的题在现行的教科书中很常见，苏科版教科书就以路灯下的影子为例引出中心投影．足以看出，今天的很多数学问题都可以在历史上找到渊源．

2 20世纪西方早期教科书中的测量之用

20世纪初，在英国兴起的培利运动和德国数学家F.克莱因领导的教育改革不谋而合，都倡导数学教育应该面向大众，强调数学的实用性．在这些思想的引领下，美国和日本也掀起了数学教育改革之风[10]．彼时的教科书也受到这场数学教育改革浪潮的影响，增加了关于数学实际应用的内容．以美国早期的几何教科书为例，相似三角形的实际应用涉及测量领域，除了与现行教科书一致的影长测高和镜面测高等实例，一些简易的测量工具也走进了几何教科书，测量情境和工具的分类见图6．为避免重复叙述，本文只介绍教科书中测量工具的原理及涉及的相似三角形，不具体展开计算步骤．

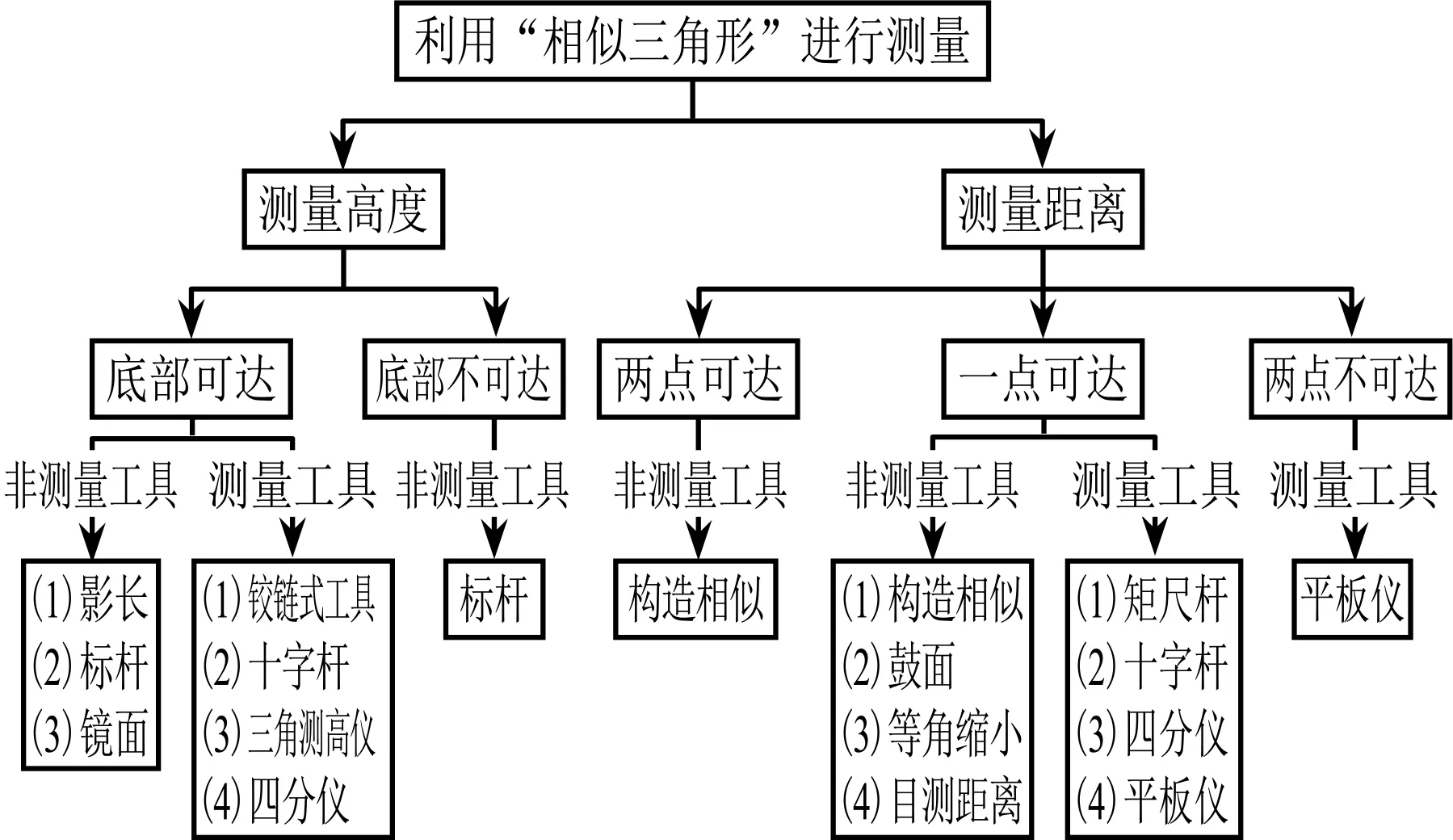
图6

2.1 底部可达的高度测量

·影长测高

影长测高法源自希腊数学家泰勒斯，他通过影长测得金字塔高度，Mallory和Stone呈现了影长测高的实例(图7)，该方法可归纳为：同一时间测量已知高度物体和待测物体的影长，通过相似比求得待测物体的高度[11]．

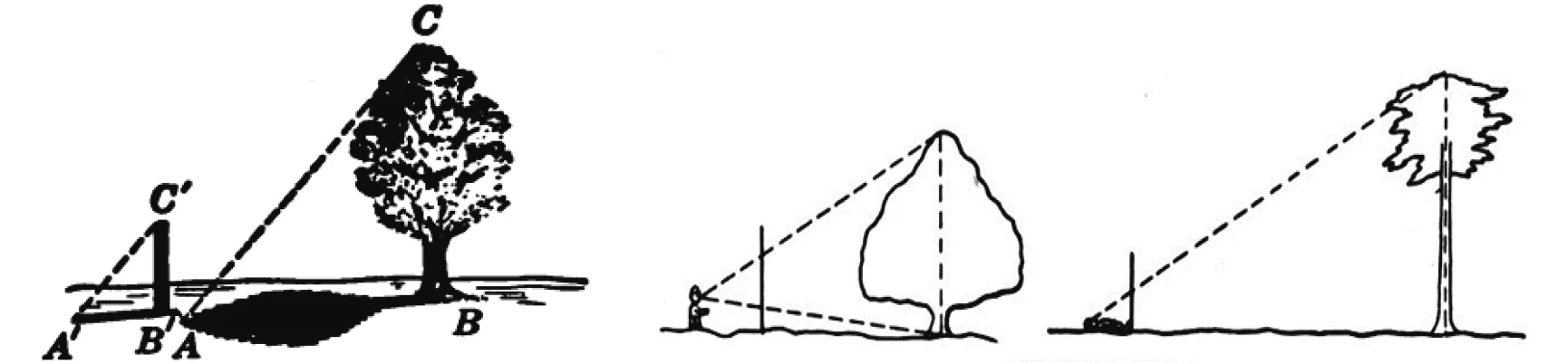
图7 影长测高 图8 标杆测高

·标杆测高

如图8，Willis在介绍标杆测高法时列举了两种情况：一是测量员站着测量(左图)，二是测量员躺着测量(右图)．显然，第二种仅适用于地面平坦的情况，需要构造直角三角形相似．而第一种则不受限制，当测量员望向被测物体的顶端和底端时，视线分别与标杆上的两点重合，只需要构造一般三角形的相似即可[12]．

·镜面测高

如图9，Auerbach和Walsh利用镜面反射测量高度，其中蕴含入射角和反射角相同(∠AMX=∠CMB)的物理原理．当地面平坦时，竖直站立的测量员AX望向点M处，恰能从镜中看到被测物体BC的顶端C，证明Rt△AXM∽Rt△CBM．在镜子被普及之前，一碗水银、墨水或者糖浆的表面可以达到同样的效果[13]．

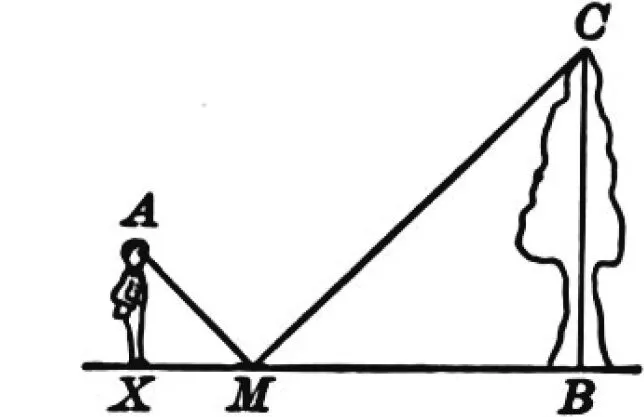
图9 镜面测高

·铰链式工具测高

Long和Brenke表示，泰勒斯用影长测高的方法只有阳光灿烂时才能起作用，若要在森林中进行测量便无法奏效，需要一种新的工具来突破这一局限．图10展示了一种自制铰链式工具，在带凹槽的金属条SR中有一根小金属条可以自由滑动．当地面平坦时，如果要测树高NL，先将QR竖直固定于地面，再将SR对准树的顶端N，小金属条顺着凹槽滑至地面点P，显然N,S,R,P四点在同一直线上，测量LP,PQ和RQ的长度，证明Rt△RPQ∽Rt△NPL[14]．

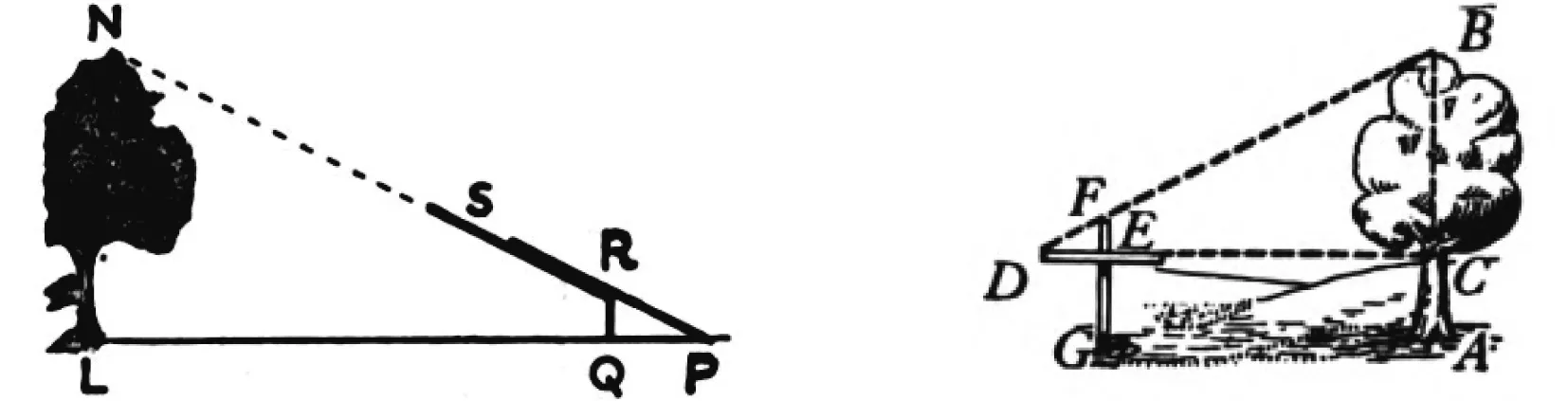
图10 铰链式工具测高 图11 十字杆测高

·十字杆测高

Stone和Millis使用十字杆(cross-staff)测量物体AB的高度(图11)，横杆DE可顺着直杆FG上下移动，使得D,F,B三点共线，测量DE,EF,CD和AC的长度，证明Rt△DEF∽Rt△DCB[15]．

·三角测高仪测高

如图12，据Willis记载，三角测高仪又叫佛斯特曼测高仪(Faustmann’s Hypsometer)，护林员常常用它来测树高．点D处有一根铅垂线(左图)，护林员从点A处透过DE上的小洞观测到树的顶端C点，此时铅垂线与EE′相交于F点，读出EF的长度，接着借助水准仪，由助手在树上标记B点(AB与地面平行)并测量BG的长度，证明△DEF∽△ABC[12]．

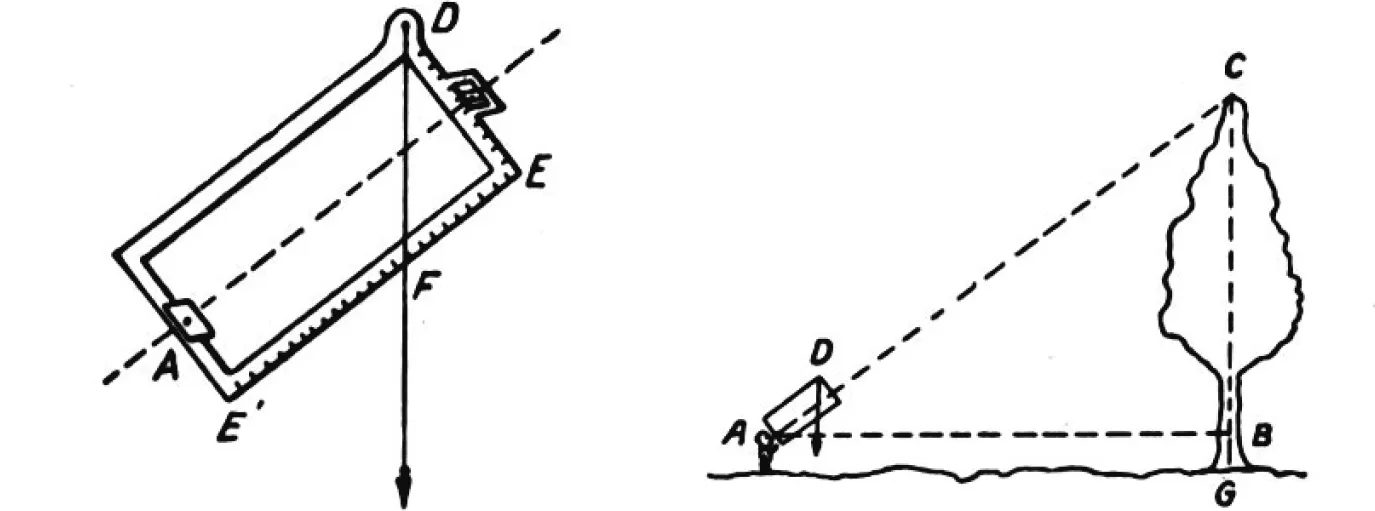
图12 三角测高仪测高

·四分仪测高

四分仪(geometric square)是一种带有铅垂线的几何方形工具(图13)．测量员将四分仪放置于地面，沿着上边缘的两个小孔望向被测物体的顶端N处(三点共线)，此时铅垂线穿过刻度点C，读出BC的长度，且AB长度已知．若地面平坦，则四边形ADMP为矩形，测量AD或PM,AP或DM的长度，证明△APN∽△ABC[15]．

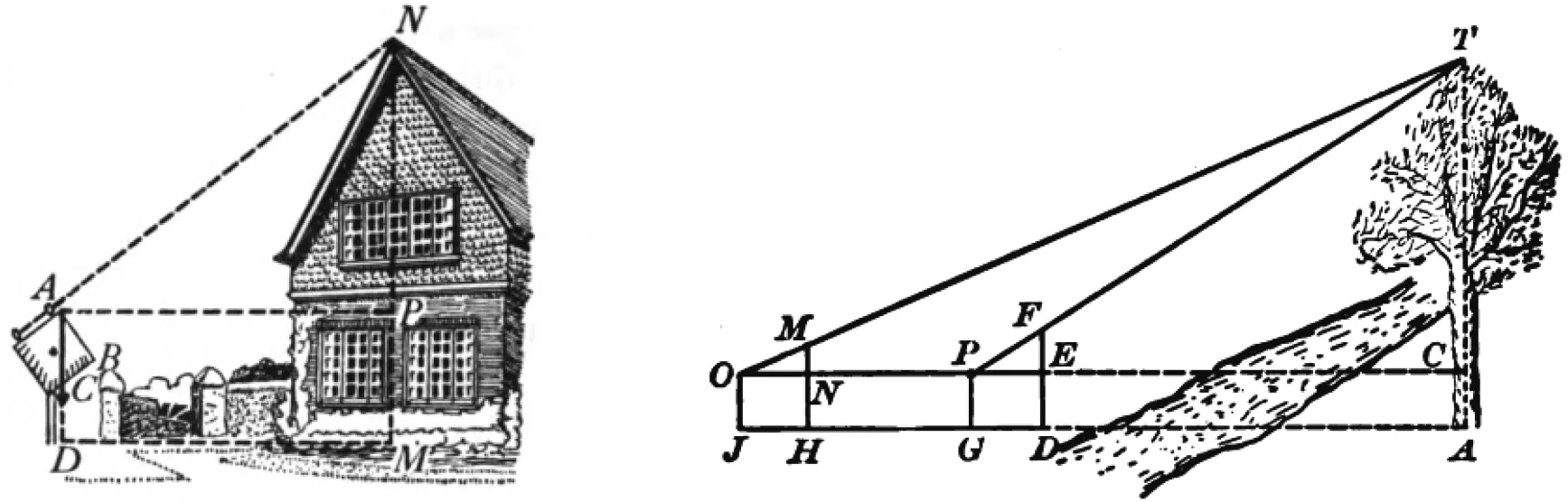
图13 四分仪测高 图14 两次标杆测高

2.2 底部不可达的高度测量

·两次标杆测高

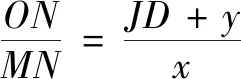
2.3 两点可达的距离测量

两点可达是指两个测量点均是可接近点，但其被障碍物隔开，测量员无法直接测量该两点间的距离．

·构造相似测距

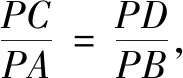
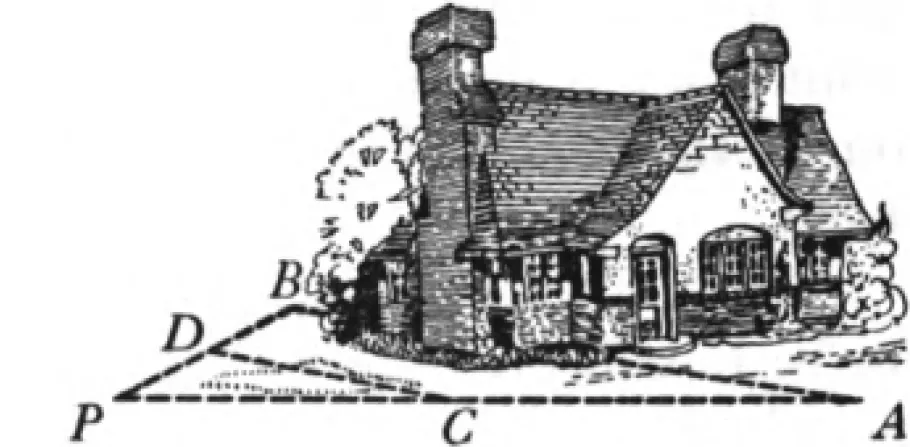
图15 构造相似测距 (两点可达)

2.4 一点可达的距离测量

一点可达是指只有一个测量点可接近，另一个测量点不可接近．

·构造相似测距

一点可达常以测量河宽为情境，若要测量岸边一点A到对岸一点B之间的距离，可以构造一对相似三角形．如图16(左)，在岸边作AD⊥AB和AD⊥DE，此时BE与AD交于点C，证明Rt△ABC∽Rt△DEC，测量AC,ED和CD的长度，通过对应线段成比例即可求出AB的距离．也可以构造一般的相似三角形见图16(右)，在AB间取一点D，任意在岸边作一条线段DE，再过点A作AC∥DE，使得C,E,B在同一直线上，取AF=DE，易证四边形AFED是平行四边形，则由平行可知△CFE∽△CAB，测量CF,EF,CA的长度，同理可求AB的距离[13]．

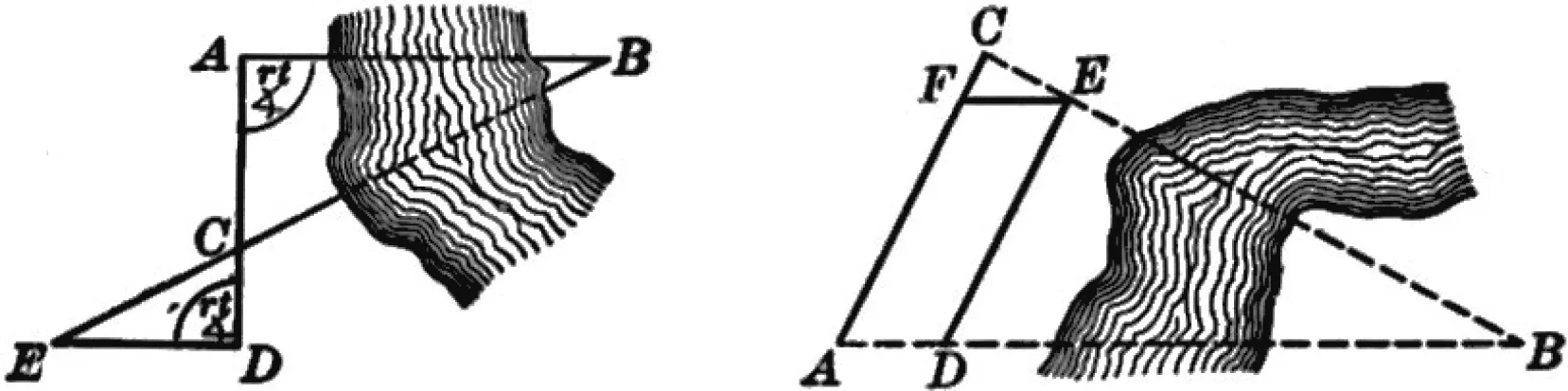
图16 构造相似测距(一点可达)

·矩尺杆测距

矩尺杆是由木杆AC和矩尺ECD组成的测量工具(图17)，其中∠ECD=90°，测量员将CD端指向点B处，此时CE端指向地面的点F处，测量FA和AC的长度，证明△CAF∽△BAC，即可求出AB的长度[15]．

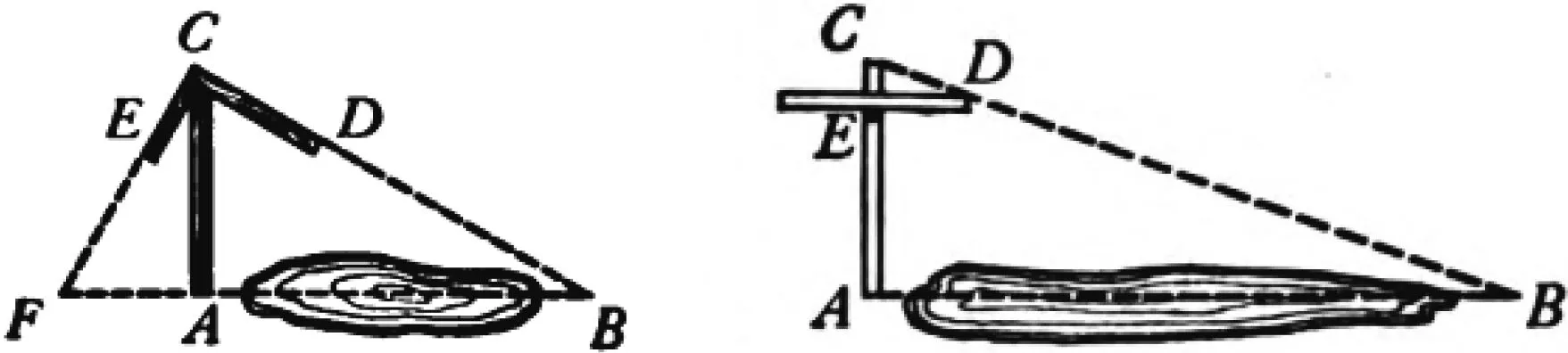
图17 矩尺杆测距 图18 十字杆测距

·十字杆测距

用十字杆测距的原理与用其测高的原理一致，如图18，将横杆DE顺着直杆AC上下移动，使得C,D,B在同一直线上，测量CE,AC,DE的长度，证明△CED∽△CAB[15]．

·四分仪测距

与十字杆一样，四分仪也可用于距离的测量 (图19)．若要测量PQ的距离，与测高的原理相同，只要测量AB,BC和AP的长度，再证明△QPA∽△ABC[15]．

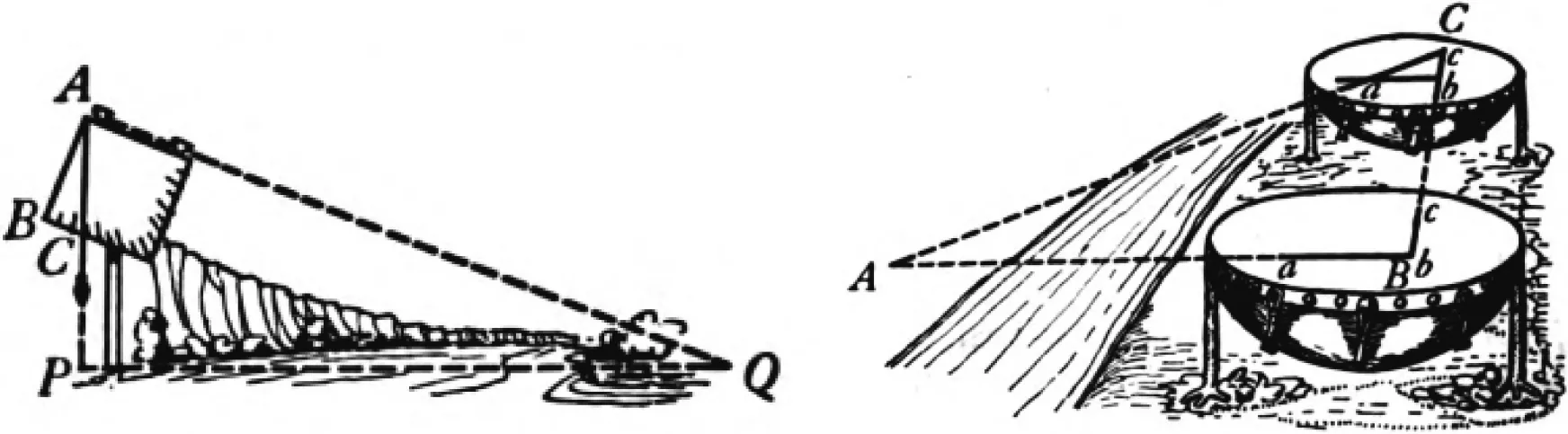
图19 四分仪测距 图20 鼓面测距

·鼓面测距

如图20，若要测量地面上AB的距离，Stone和Millis将鼓面(drum heads)放置于地面上的点B处，从鼓面上点b沿BA方向作一条方向线ba(点b与点B在同一垂线上)，在地面上选取一点C，再沿BC方向作线段bc，将鼓面沿BC方向移至点C处(点c与点C在同一垂线上)，从鼓面上的点c沿CA方向作直线，交方向线ba于点a．测量BC,bc,ba的长度，证明△abc∽△ABC[15]．

·平板仪测距

平板仪(plane-table)一般用于制作地图时定位和查找距离，其由图板和三角架组成，见图21(左)，图板上有一把直尺，在直尺的首、末端各有一个观测点S和S′，通常会在上面放望远镜．例如，要测量PQ的距离，见图21(右)，首先在地面和图板上过点P作一条基线MN，将直尺的S端与点P重合，旋转直尺使得S，S′和Q三点共线，从点P沿尺画条方向线．再将平板仪从T处沿MN平移至T′处，则点P对应移动到点P′处，接着将直尺S端放在P′N上任意点K处，旋转直尺使得S，S′和Q三点共线，此时SS′交方向线于点L，构造出△P′KL，测量PK,P′K,P′L，证明△P′KL∽△PKQ．平板仪与鼓面的测距方法相同，前者的操作更加便捷[17]．

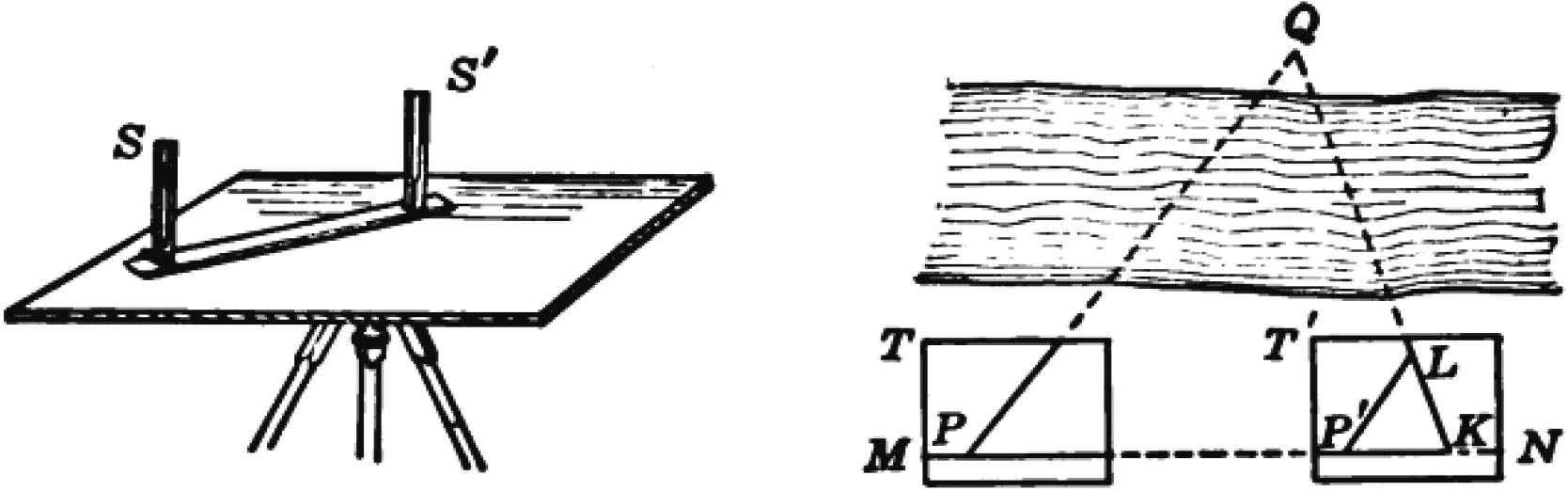
图21 平板仪测距(一点可达)

·等角缩小测距

如图22，若要测量AB的距离，选取长度可测的AC为基线，测量∠ACB和∠CAB的大小，接着在纸上作一线段A1C1(AC是A1C1的n倍)，再作∠ACB=∠A1C1B1和∠CAB=∠C1A1B1，显然△ABC∽△A1B1C1，则AB=nA1B1．这种等角缩小测距法主要用于军事[18]．

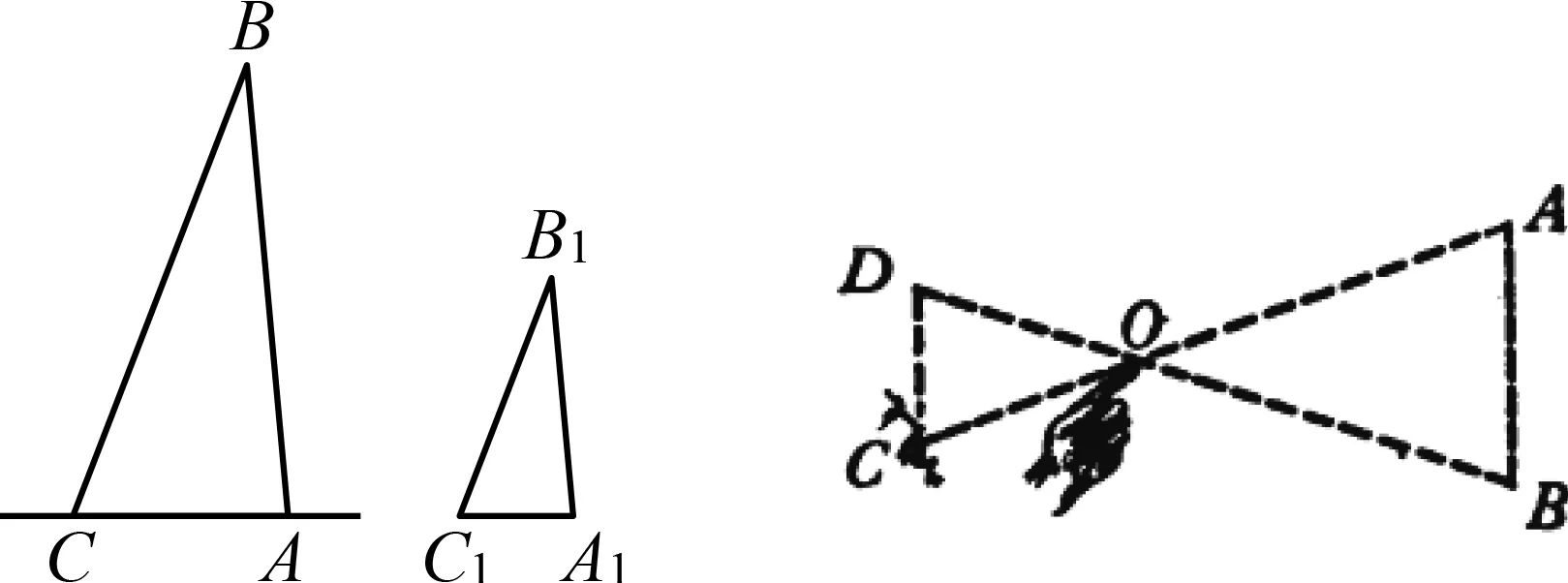
图22 等角缩小测距 图23 目测距离法

·目测距离法

在军事领域，目测距离法更加便捷，但测量误差较大.如图23，首先，观测者伸直手臂并伸出一根手指，闭上左眼，观察到指尖与物体A重合．接着睁开左眼、闭上右眼，观察到物体移至点B处，AB是交换眼睛后物体移动的距离，已知臂长约为眼间距的10倍，通过相似三角形对应边成比例的原理，可以估测AO间的距离，进而计算AC间的距离．例如一艘战舰长度为172 m，用上述方法在海上观察时，发现战舰似乎移动了四条船的长度，则距离约为172×4×10=6 880 m[15]．

2.5 两点不可达的距离测量

两点不可达是指两个测量点均不可接近．

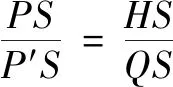
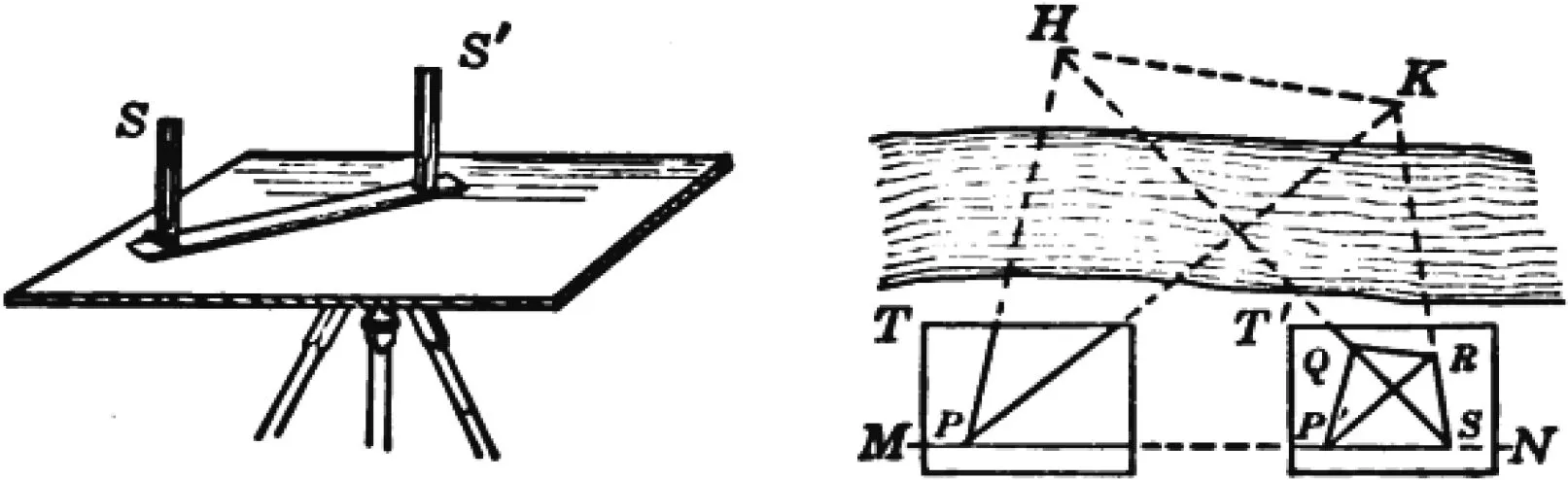
图24 平板仪测距(两点不可达)

3 结论与启示

在三角学出现以前，相似三角形在早期的测量领域中具有非常重要的应用价值，解决了很多生活中的问题.相似三角形应用的历史为今天的课堂教学提供了许多启示．

(1)基于同一情境设计不同层次的问题，构建问题串

若以大禹治水为背景，参照图6将测高问题由底部可达变成底部不可达，将测距问题由两点可达到一点可达，再变成两点不可达，问题难度层层递进.假如学生是大禹，他将会如何解决这些测量问题呢？再将学生的解决方案进行古今对照，与古人跨时空对话，增强他们学习数学的信心．

(2)开展综合实践活动，培养学生的创造力

《义务教育数学课程标准(2022年版)》(下称《标准》)强调了要进一步加强综合与实践领域的教学活动，以真实问题为载体，培养学生的创新意识和实践能力等综合品质[19]87．虽然早期科技并不发达，但也出现了一些凝聚智慧的测量工具，这些工具体现了测量员们的创新精神．若以测量校园内某一物体的高度为实践活动，要求学生自主设计测高或测距工具进行测量，他们会想到哪些方法？又会制作出怎样的测量工具呢？答案是令人期待的．学生在解决问题的过程中获得数学活动经验，感悟数学的价值，进而对数学产生好奇心和求知欲．

(3)依托信息技术，创新教学方式

历史上关于相似三角形应用的素材非常丰富，然而课堂的时间十分有限，若将其都编成数学问题则不现实，若是以大段文字材料的形式呈现又显乏味．教师可以把相关素材制作成一个微视频，通过一个主题，讲好一段故事，展现数学人文的一面，让学生体会到数学源于生活又应用于生活，从而建立良好的数学观，激发学习数学的兴趣．

(4)融传统文化于课堂，实现德育之效

《标准》提倡在数学课程中弘扬中华优秀传统文化[19]2，教师可以发挥《周髀算经》、重差术等优秀传统文化的育人功能，帮助学生了解和领悟中华民族独特的数学智慧，增强文化自信和民族自豪感．