五轴重型特种车辆的状态估计及验证
于传强, 舒洪斌, 刘志浩, 陈渐伟, 高 杨
(1. 火箭军工程大学 导弹工程学院, 西安 710025; 2. 火箭军装备部驻长治地区代表室, 山西 长治 046000)
随着军事化需求的推进,特种车辆行驶环境复杂多变,加上特种车辆载重大、质心高等特点,在机动过程中易造成车辆操纵失稳等事故。为了更好的判断车辆行驶过程中的状态变化,减小事故发生的可能性,借助有限的传感器,基于动力学模型和参数估计方法,来获取尽可能符合实际的状态参数,是一种经济有效的方法[1-3]。
近年国内外的研究学者通过无迹卡尔曼滤波(unscented Kalman filter, UKF)及其改进算法对车辆的运动状态参数进行研究成为一主要的估计方法,并取得了一些成果。Antonov等[4]基于建立的动力学模型采用UKF估计车辆的轮胎滑移率和质心侧偏角,在进行试验后验证了该估计算法具有较高的精度和较好的收敛性。赵万忠等[5]利用UKF算法对车辆状态进行了实时估计,并将Carsim和Simulink 联合仿真进行验证,结果表明,采用UKF算法响应快,估计精度要高于扩展卡尔曼滤波(extended kdman filter, EKF)。Doumiati等[6]对基于EKF和UKF的车辆质心侧偏角估计器进行了性能对比,结果证明无迹卡尔曼滤波在估计精度上具有一定优势。Gu等[7]以两轴分布式驱动车辆为研究对象,建立非线性 7 自由度车辆动力学模型,采用UKF算法对纵向速度、侧向速度和横摆角速度进行了联合估计,试验结果表明该算法估计精度更高。上文所述皆为四轮小型车的状态估计,且试验结果表明无迹卡尔曼滤波的估计精度更高,针对多轴重型车辆运动状态估计的研究则较少。
因此,本文以五轴重型车辆为研究对象,设计了基于无迹卡尔曼滤波(UKF)的状态估计器,并以经过实车验证的13自由度仿真平台开展状态估计研究,来验证估计算法的有效性和估计精度。
1 车辆动力学模型搭建及验证
1.1 整车模型搭建
分析五轴车辆的动力学特性,基于车辆动力学理论,建立较为完善的整车动力学模型,为算法验证提供高保真的仿真平台,以进行不同工况下的仿真验证。
建立包括纵向、侧向、横摆和每个车轮的转动,总共十三自由度的车辆模型。
1.1.1 车体动力学模型
如图1所示为车辆在xoy平面的运动,忽略了车辆的俯仰运动和侧倾运动,且不考虑车辆的滚动阻力、迎风阻力和空气阻力等,得出五轴特种车辆在纵向、侧向以及横摆运动的运动平衡方程如下[8]

图1 车辆整体模型Fig.1 Overall vehicle model
纵向运动微分方程
(1)
侧向运动微分方程
(2)
横摆运动微分方程

l2(Fy2l+Fy2r)-l3(Fy3l+Fy3r)-
l4(Fy4l+Fy4r)-l5(Fy5l+Fy5r)
(3)
式中:m为整车质量;g为重力加速度;li为各轴到质心的距离;B为车辆轮距;vx为纵向速度;vy为侧向速度;Iz为车辆绕z轴的转动惯量;wz为车身横摆角速度;Fxil和Fxir为第i轴左、右侧轮胎的地面纵向力,Fyil和Fyir为第i轴左、右侧轮胎的地面侧向力。在轮胎坐标系上,第i轴左、右侧纵向力表示为Fxwil和Fywir,侧向力表示为Fywil和Fywir。车辆坐标系与轮胎坐标系之间的轮胎力的关系式为
(4)
式中,α为车轮侧偏角。
1.1.2 车轮运动模型
考虑车轮在平面内的旋转自由度,建立车轮的运动模型如图2所示。不考虑地面侧向力的影响,在车轮旋转运动的方向上,车轮受到驱动力矩Ti、制动力矩Tbi、反力矩Tdi[9];由于轮胎的弹性和地面的摩擦作用,垂向力的作用点偏前于轮胎接地印迹几何中心一个距离还对轮心形成一个滚动阻力矩
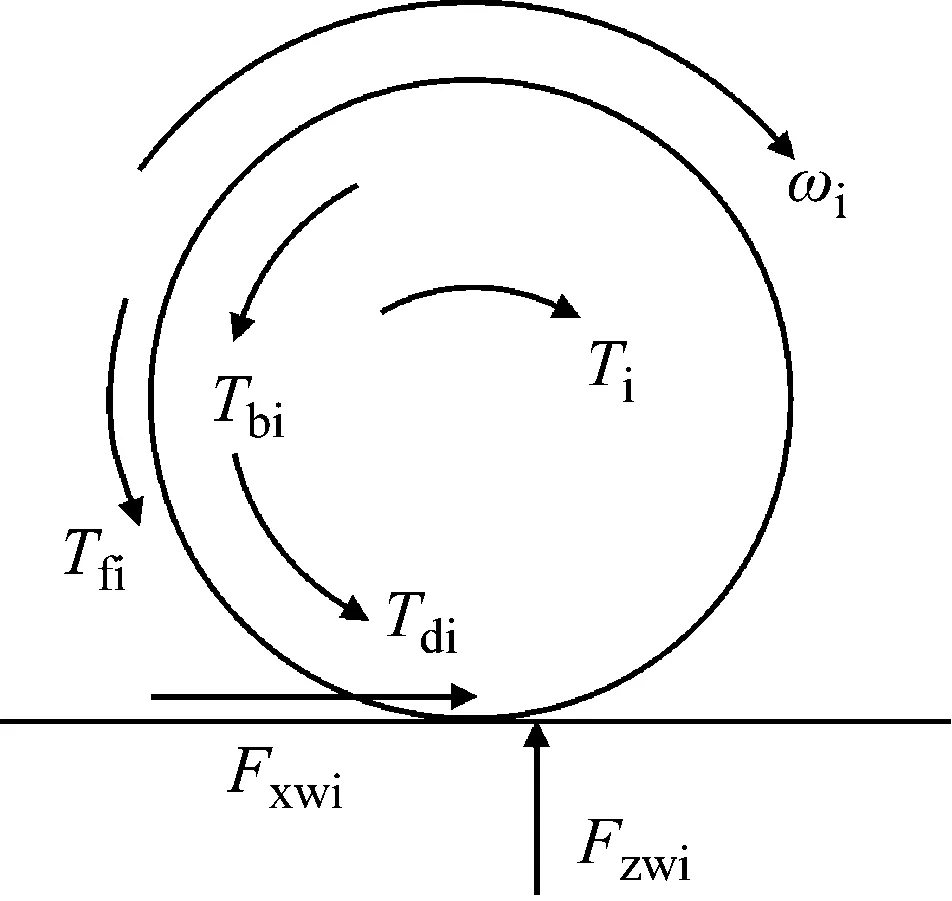
图2 车轮受力模型Fig.2 Wheel force model
Tfi=FziΔi=Fzifrrw
(5)
式中:Fzi为地面对轮胎的作用力;fr为滚动阻力系数;rw为轮胎滚动半径。
将作用于车轮上的力和力矩对轮心取力矩,得到车轮滚动方程
(6)
式中:Iw为车轮转动惯量;ωi为车轮旋转角速度。
1.1.3 轮胎模型
轮胎作为车辆与地面的一个交互部件,它的建模精度直接影响着整车模型仿真结果,魔术公式(magic formula)轮胎模型能够较为精确的表征轮胎的非线性,采用魔术公式轮胎模型来描述轮胎的动力学特性。它的表达公式为
(7)
式中:y为轮胎纵向力或侧向力;x为轮胎侧偏角或滑移率;Sv为垂直偏移量;Sh为水平偏移量;B、C、D、E分别为刚度因子、形状因子、峰值因子、曲率因子,其数值可通过参数辨识得到。由于该类车型所使用的重载子午轮胎具有垂向载荷范围大、扁平比大的特点,因此本文采用文献[10]中针对重载工况下的魔术公式修正模型。由式(7)可知,轮胎力的计算需要侧偏角和滑移率的输入,接下来计算这两个值。
因为本文中的建模忽略侧倾和俯仰运动对速度产生的影响, 由于车辆横摆运动的缘故,各轮轮心的速度可由车辆质心速度和横摆角速度表示,则各个轮心的纵向速度和侧向速度为
(8)
vyi=vy±liwz
(9)
轮心沿纵轴方向的速度为
vi=vxicosδi+vyisinδi
(10)
得各个轮胎的侧偏角αi和滑移率λi为
(11)
(12)
式中:δi为各轴车轮转角;ωi为各车轮旋转角速度。
1.1.4 转向系统运动学模型
建立如图3所示的阿克曼转向模型,在阿克曼转向模型中,为了使所有车轮处于纯滚动或只有极小滑动的状态,要求所有车轮具有同一个瞬时转向中心,该五轴车的1、2、4、5轴为转向轴,瞬时转向中心位于三轴的延长线上。为简化转向模型,假定车辆转向系统的传动比不变为isw,传动比为方向盘转角和一轴左侧轮胎转角的比值,方向盘转角为δsw,根据图3得出各个车轮转角的几何关系:

图3 阿克曼转向模型Fig.3 Ackerman steering model
(13)
1.1.5 整车模型集成
通过Matlab/Simulink实现的整车集成模型,输入方向盘信号给转向模块,转向模块通过Matlab Function函数表示出前两轴和后两轴的8个转向轮的转角并输出给车辆运动模块。车辆运动模块的输入包括 8 轮转角和 10轮转矩,输出为10轮转速和纵向速度、纵向加速度、侧向速度、侧向加速度和横摆角速度等,若在后续研究中需要其他参数,可在Simulink中增加相应的输出。
1.2 实车试验验证
为了验证所搭建模型的准确性,利用所具有的特种车辆行驶状态监测系统进行实车验证。实车试验方案为:方向盘转角传感器采集转向信息、SPEEDBOX-INS车辆姿态测量系统、卫星导航传感器等实时获得车辆运行过程中车速、轨迹、高程、车辆姿态、横摆角速度等信息,通过CAN总线输出至拥有多通道、多参数的DEWE43数据采集系统,用Race Technology和DEWEsoftX3软件对试验数据进行记录分析处理,具体试验过程如图4所示。

图4 实车试验Fig.4 Real vehicle test
车辆模型验证的过程如图5所示。将试验测得的方向盘转角δexp、纵向速度Vx,exp作为整车模型的输入,其中速度控制模型根据作为期望速度的纵向速度Vx,exp和当前模型实际车速Vx,mod,将对应的驱动力或制动力传给整车模型的车轮运动模块。将仿真模型得到的纵向速度Vx,mod、横摆角速度wz,mod、侧向加速度ay,mod与试验数据进行比较。因为搭建的模型目的是作为状态观测的仿真平台,所需观测的纵向速度是各类控制算法中重要的输入参数,且横摆角速度和质心侧偏角状态量是以横向动力学模型为基础,横摆角速度与侧向加速度二者有研究用来验证模型的准确度[11]。根据试验数据与仿真数据的差值,通过试错调整模型参数,最终确定最小均方根误差下的模型。
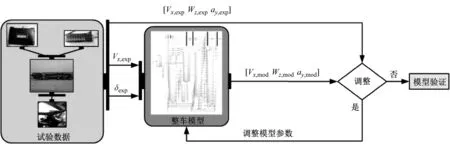
图5 验证模型Fig.5 Validate the model
基于现有的试验条件,安装好试验器材后在某段高原公路与砂石路上进行实车试验,选取的验证路况分别为近乎直线行驶路段和带有两处较大拐弯路段,将选取路段的数据信息用于车辆模型参数调整与验证。
路况1该路段为近乎直道行驶路段,主要为砂石路,较为颠簸。实车行驶轨迹、方向盘转角分别为图6、图7;模型与实际值的纵向速度、横摆角速度和侧向加速度对比图分别为图8(a)~(c)。

图6 实车行驶轨迹图Fig.6 Real vehicle driving trajectory map

图7 方向盘转角Fig.7 Steering wheel angle

(a) 纵向速度对比
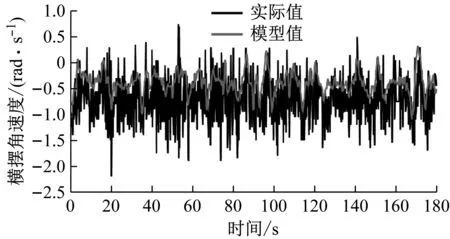
(b) 横摆角速度对比

(c) 侧向加速度对比图8 模型验证对比Fig.8 Model validation comparison
路况2该路段为带有两处较大弯道行驶路段,主要为柏油路与砂石路。实车行驶轨迹、方向盘转角分别为图9、图10;模型与实际值的纵向速度、横摆角速度和侧向加速度对比图分别为图11(a)~(c)。

图9 实车行驶轨迹图Fig.9 Real vehicle driving trajectory map

图10 方向盘转角Fig.10 Steering wheel angle

(a) 纵向速度对比
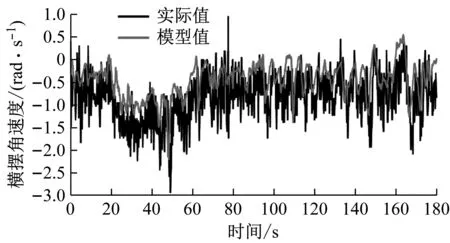
(b) 横摆角速度对比

(c) 侧向加速度对比图11 模型验证对比Fig.11 Model validation comparison
将实车所得的横摆角速度和侧向加速度去噪处理,实车数据与模型输出数据的均方根误差如表1所示,由图8、图11以及表1可知,实际值与模型输出的纵向速度、横摆角速度以及侧向加速度对比,二者会有一些误差,但总体上变化趋势与实际相符,较为吻合。其原因是数学模型中忽略了悬架的动态载荷且模型中轮胎的转角和实际转角会有一些误差,进而导致簧上质量的载荷转移有些误差,且实车试验环境为开阔的高原公路与砂石路,起关键因素的轮胎会与平原的胎压有所不同,魔术公式轮胎模型的参数拟合会有所差异,间接影响轮胎与地面相应的作用力,同样会受风速尤其是侧向风速、路面不平整度等一些因素的影响。该实车试验验证结果能够说明该模型可用于状态估计器的仿真验证。最终调整验证模型过程中,在原有车辆数据的基础上,主要对转向系传动比、车辆质量绕z轴转动惯量这几个参数做微调。在调整验证过程中,转向系传动比的变化对横摆角速度与侧向加速度的变化影响较大,实车转向系传动比随着档位的变化而变化,模型中将其作为一个定值,所以传动比是调整变化较大的一个参数,按照均方根误差数值最小的调整基准,模型最终确定的主要参数数值如表2所示。

表1 均方根误差Tab.1 Root mean square error

表2 车辆参数Tab.2 Vehicle parameters
2 UKF观测器设计
2.1 五轴车观测方程
所建立的车辆模型自由度多,且会因模型的复杂度等影响估计的实时性,因此在建立状态方程时将13自由度的模型降为三自由度车辆模型,作为多轴车辆状态估计模型。
为研究车辆行驶的操纵稳定性,3自由度车辆模型考虑了纵向、侧向、横摆方向的运动,车辆模型的动力学平衡方程为[12]
纵向运动微分方程
(14)
侧向运动微分方程
(15)
横摆运动微分方程
(16)
非线性系统的状态空间方程可以表示为
(17)
式中:xk+1,zk,uk分别为系统状态量、观测量和输入量;wk和vk分别为过程噪声和观测噪声。
根据所建立的车辆动力学模型,方向盘的转角及纵向加速度可以通过传感器精确测量,二者作为输入变量为
u=[δax]T
(18)
式中:δ为方向盘转角;ax为纵向加速度。
三维状态变量为
x(t)=[wzβvx]T
(19)
式中:wz为横摆角速度;β为质心侧偏角;vx为纵向速度。
横向加速度ay为观测量[13]。
2.2 系统估计方程
利用UKF滤波算法进行状态估计,建立系统估计方程。
UKF利用相似分布原理,计算的Sigma点集跟原分布均值和协方差一样,带进非线性系统后进行无迹变换,进而得出估计量:
步骤1计算Sigma采样点χ(i)并求出采样点的权值ω(i)
(20)
(21)
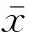
步骤2用式(20)重新求得Sigma点集和其相应权值并计算Sigma点的进一步预测。
χ(i)k=
(22)
(23)
进而求出状态量预测和协方差矩阵的预测
(24)
(25)
步骤3将步骤2计算出的状态预测量通过无迹变换计算出预测量的采集样点
(26)
计算Sigma点的预测观测量
(27)
求观测的预测均值,得出预测的均值及协方差
(28)
(29)
(30)
步骤4计算卡尔曼增益矩阵
(31)
步骤5更新状态量和协方差矩阵[14]
(32)
(33)
根据以上公式可得出三自由度整车状态方程及测量方程
(34)

(35)
式中:ki为侧偏刚度;k1i为各轴轮胎转角与一轴的比例值。
3 观测器虚拟验证
在Simulink中将建立的十三自由度整车动力学模型与UKF整合,如图12所示,利用经过试验验证过的高保真模型进行仿真验证。车辆先加速到20 m/s,在到达20 m/s后分别对方向盘进行角阶跃输入、角脉冲输入和正弦输入验证。

图12 估计算法仿真验证Fig.12 Simulation verification of estimation algorithm
工况1在角阶跃输入工况中,车辆匀加速到20 m/s后,在35 s时对方向盘转角进行角阶跃输入如图13(a)所示,纵向速度、横摆角速度和质心侧偏角的估计值和实际值如图13(b)~(d)所示。
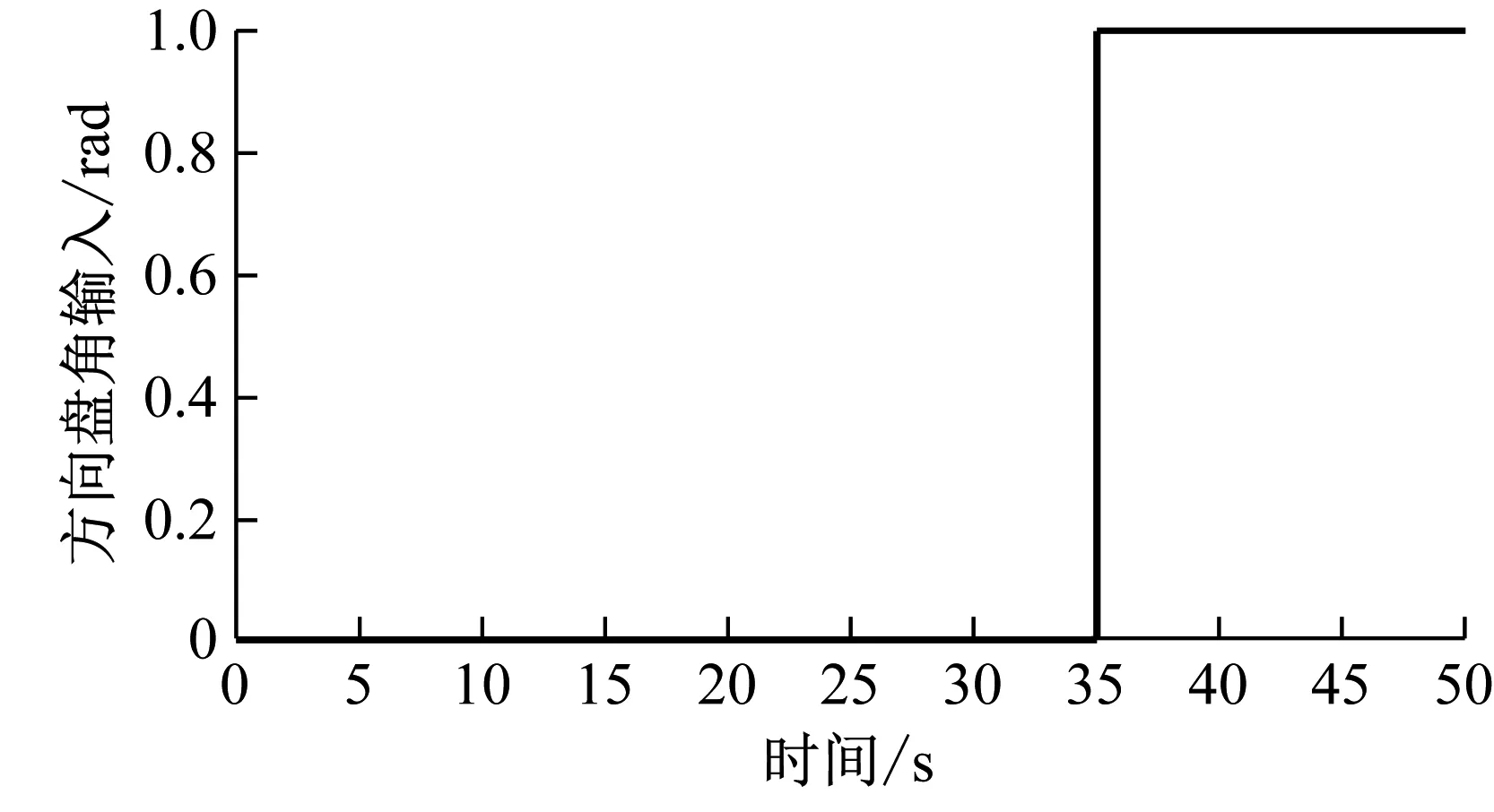
(a) 方向盘转角
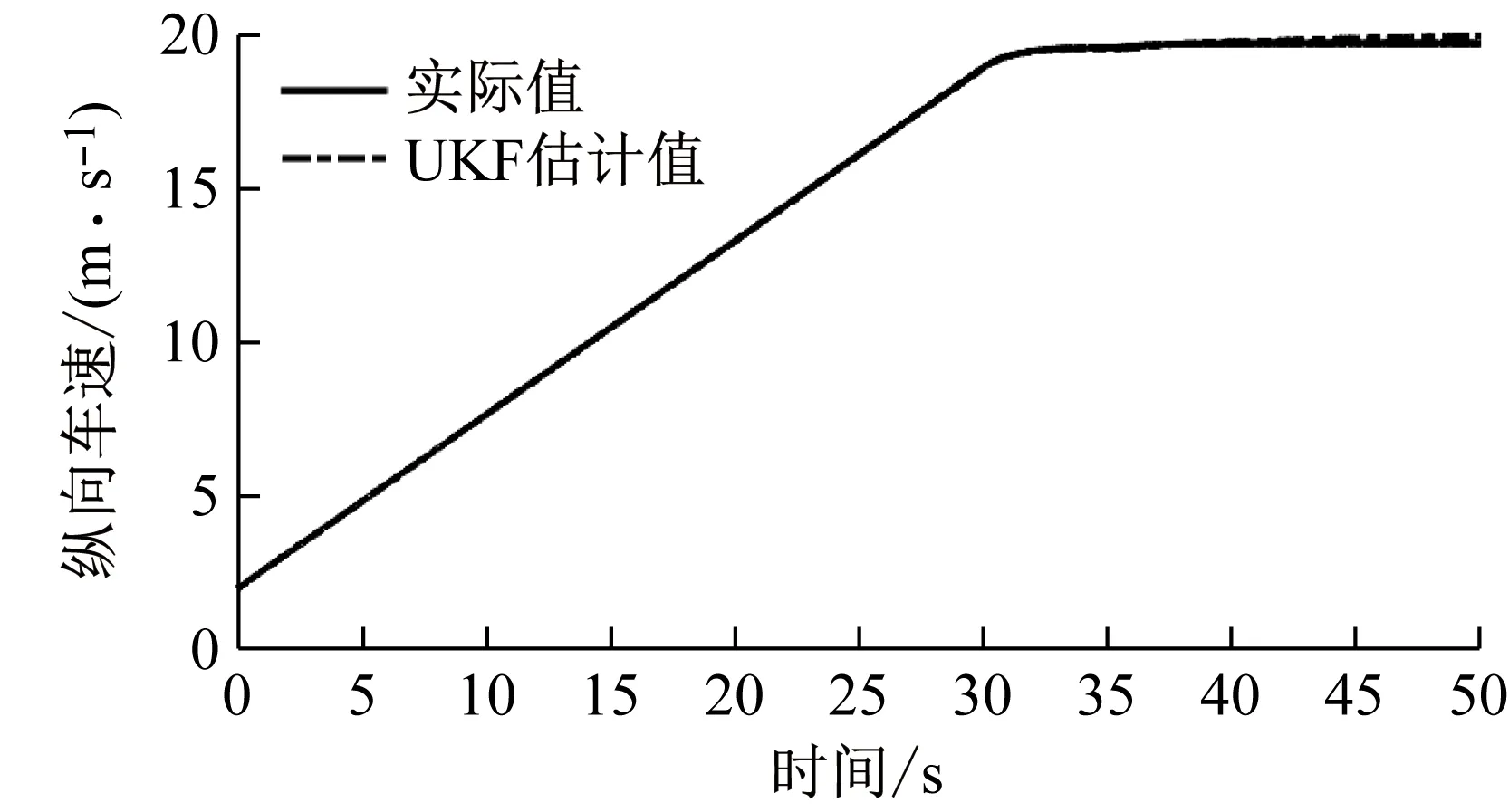
(b) 纵向速度

(c) 横摆角速度
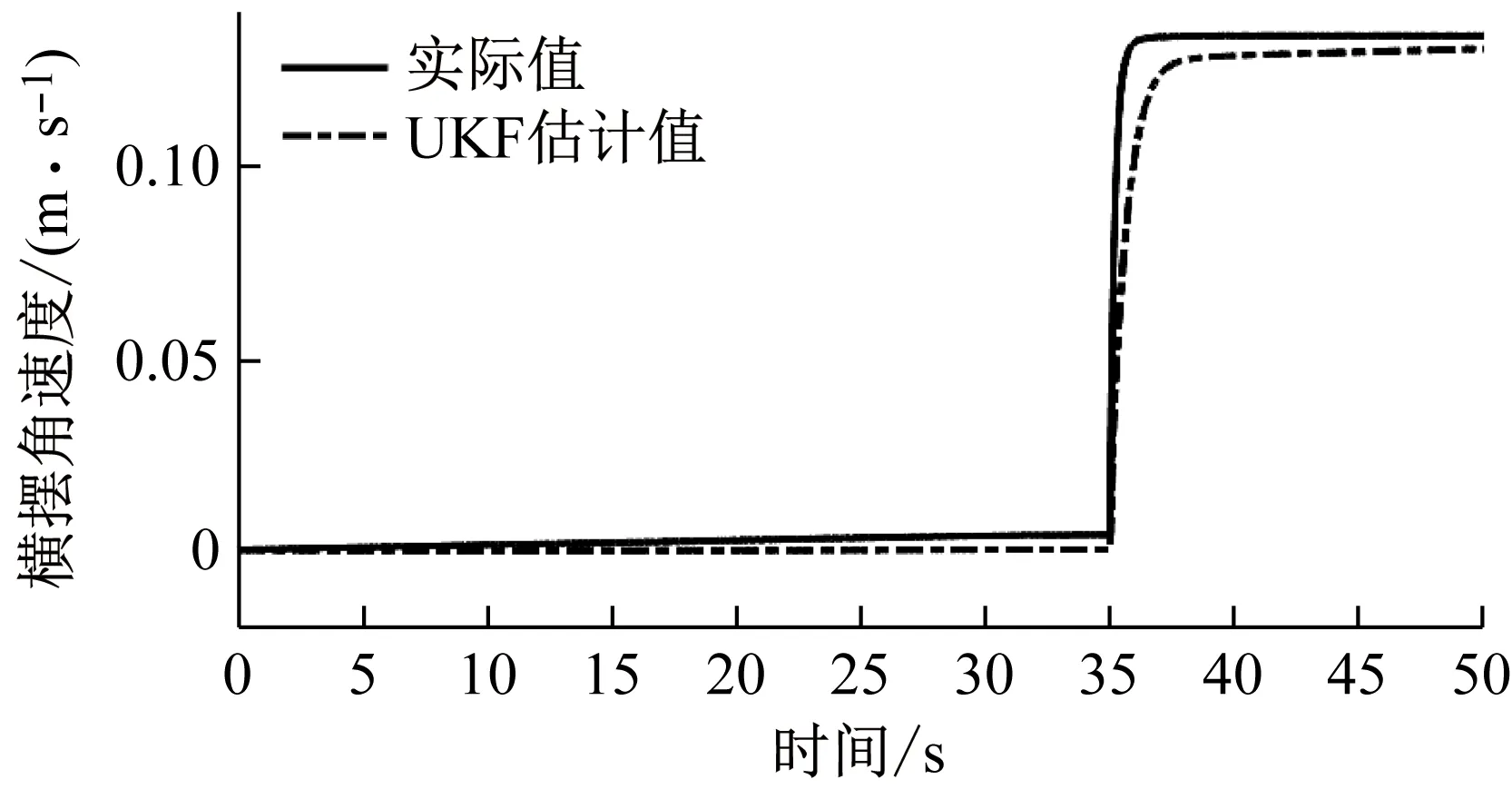
(d) 质心侧偏角图13 角阶跃输入的UKF估计结果Fig.13 UKF estimation result of angular step input
工况2在角脉冲输入工况中,车辆匀加速到20 m/s后,在35 s时对方向盘转角进行角脉冲输入如图14(a)所示,纵向速度、横摆角速度和质心侧偏角的估计值和实际值如图14(b)~(d)所示。

(a) 方向盘转角

(b) 纵向速度

(c) 横摆角速度

(d) 质心侧偏角图14 角脉冲输入的UKF估计结果Fig.14 UKF estimation result of angular pulse input
工况3在正弦输入工况中,车辆匀加速到20 m/s后,在35 s时对方向盘转角进行正弦输入如图15(a)所示,纵向速度、横摆角速度和质心侧偏角的估计值和实际值如图15(b)~(d)所示。
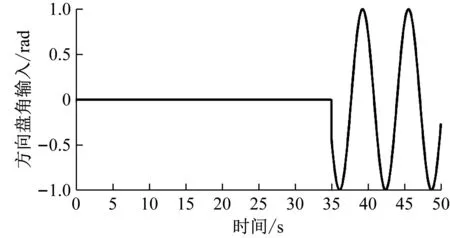
(a) 方向盘转角
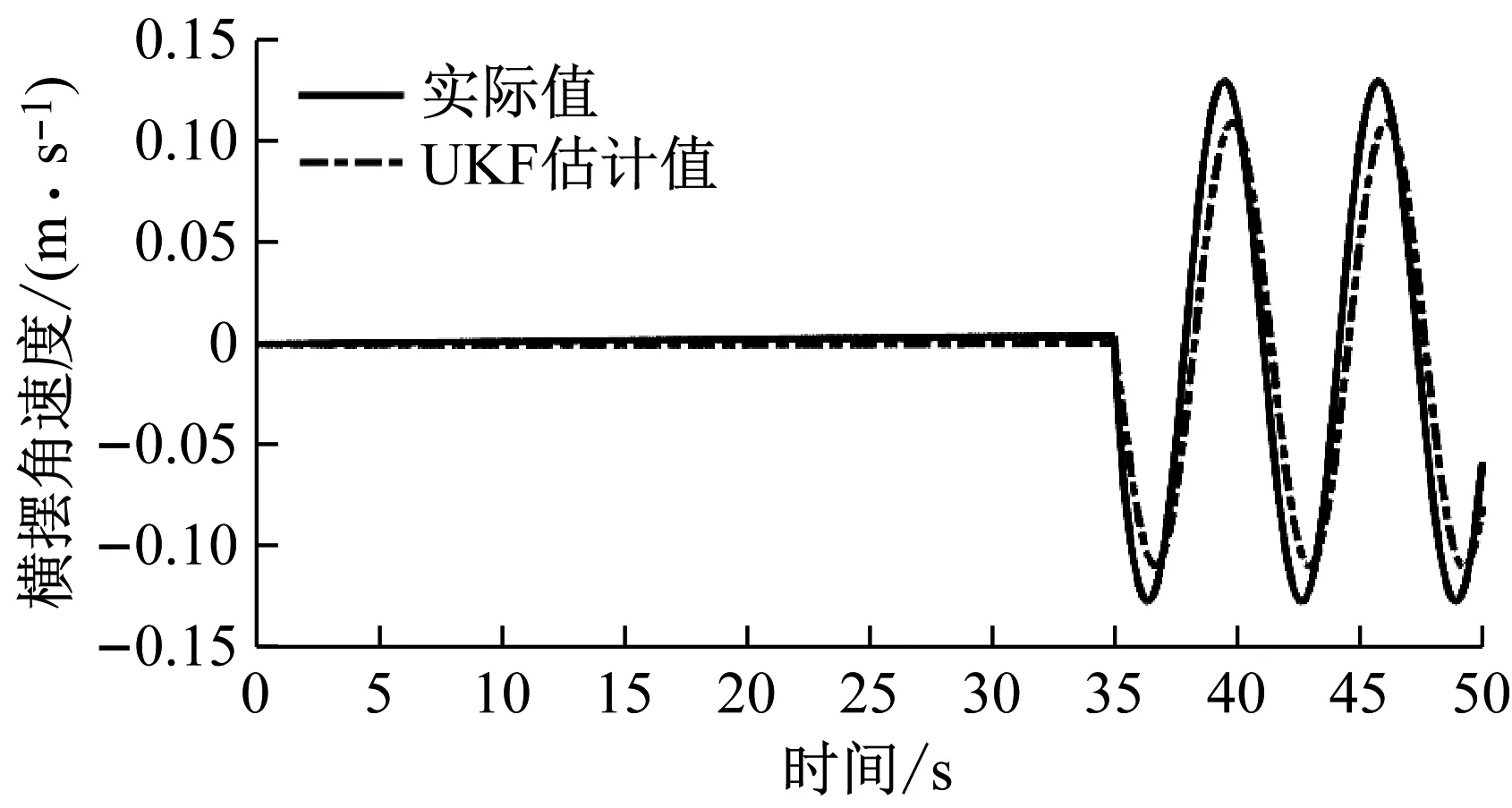
(c) 横摆角速度

(d) 质心侧偏角图15 正弦输入的UKF估计结果Fig.15 UKF estimation result of sinusoidal input
三种工况下的均方根误差如表3所示。由图13、图14、图15和表3可知,在车辆直线匀加速行驶阶段,三种工况下的纵向速度几乎是吻合的,经计算此阶段的纵向速度均方根误差仅为0.008 4 m/s,横摆角速度和质心侧偏角的估计会随着速度的增大而有些偏差,均方根误差为0.001 6 rad/s和0.000 17 rad。

表3 均方根误差Tab.3 Root mean square error
在速度稳定后的匀速行驶阶段,方向盘转角发生突变时,纵向速度和质心侧偏角能够保持较好的跟随性,且三种工况下的质心侧偏角均方根误差均值为0.003 8 rad。在这个阶段,三种工况下的横摆角速度误差在角脉冲输入中出现最大差值为0.048 rad/s,但很快会趋于稳定并误差缩小。在正弦输入工况下,汽车行驶状态时刻发生变化,横摆角速度的估计结果能够对实际值保持良好的跟随性。横摆角速度的误差主要在峰值和峰谷处,其原因在于UKF估计器中初始协方差数值的设置,协方差大小的取值影响着横摆角速度和质心侧偏角的估计精度,考虑到质心侧偏角在实际测量中困难更大,设备价格更高的原因,在本文中的估计器中所设置的大小更符合质心侧偏角的估计,对于横摆角速度相对而言差一些,这需要在后期做进一步的参数辨识以及测量噪声和过程噪声自适应的改进。
本文还对30 s匀加速过程中进行正弦输入,即加速阶段的转向验证,纵向速度、横摆角速度和质心侧偏角的均方根误差分别为0.027 9 m/s、0.008 3 rad/s和0.004 9 rad。
综上结果表明该状态观测器精度较高,可实现对纵向速度、横摆角速度和质心侧偏角参数的动态估计。
4 结 论
(1) 针对五轴重型车辆搭建整车13自由度模型,依据现有的试验条件将试验测得的参量作为模型的输入,将可以反应车辆状态的关键参数-纵向速度、横摆角速度与侧向加速度作为验证对比的对象,在综合分析后到试验结果表明所搭建模型能够作为算法验证的仿真平台。
(2) 面向五轴重型车辆设计了基于无迹卡尔曼滤波的状态估计器,通过13自由度模型分别在方向盘角阶跃输入、角脉冲输入和正弦输入工况下进行验证。验证结果表明,五轴重型车辆的行驶状态发生改变时,所设计的估计器能够较精确的估计出状态参数,具有良好的跟随性,算法精度高,可为后续的车辆稳定性控制提供可靠的参数。
(3) 本文所搭建的未考虑车辆应用的实际场景,会导致仿真结果与试验结果有偏差,后续要结合五轴重型车辆的作业环境搭建仿真精度更高的整车模型。且在实车试验验证中,因试验条件以及试验环境的限制,现只能对车辆的横摆角速度与侧向加速度进行验证,在今后的试验中,需着重考虑质心侧偏角、轮胎力等参数的对比验证。

