基于滑移非理想赫兹接触的滚动轴承振动特性分析

涂文兵， 张桂源， 罗 丫， 陈 超， 梁 杰， 杨本梦

(华东交通大学 机电与车辆工程学院，南昌 330013)

滚动轴承因其特殊结构和工作原理，广泛应用于航空发动机、高速列车和数控机床等旋转机械中。随着机械系统的可靠性和精度要求日益提高，滚动轴承的振动特性也变得愈发重要，在故障诊断、机械系统检测和滚动轴承设计等领域中，轴承振动信号也作为一项非常重要的指标得到广泛应用[1-3]。因此对轴承振动特性的深入探究也具有十分重要的意义。

目前，国内外学者主要是基于理想赫兹理论建立滚动轴承动力学模型，对轴承的振动特性和机理进行了大量研究。Sunnerjo[4]最先建立了滚动轴承动力学模型分析了轴承的振动特性。Fukata等[5]简化了轴承转子系统，采用数值仿真对轴承的非线性振动特性进行分析。Lioulios等[6]基于赫兹理论建立了轴承动力学模型，研究转速波动工况下轴承的振动特性。Alireza提出了一种缺陷故障非线性动力学模型，该模型能准确预测滚动体过故障的加速度振动频率。常斌全等[7]基于Sunnersjo建立的模型进行改进，通过时、频域信号分析了故障轴承的振动特性。Shah等基于非线性赫兹理论，建立考虑油膜刚度的轴承动力学模型，研究了载荷、转速和波纹度等对轴承振动频率和振动幅值的影响。余伟光等[8]基于线性回归对赫兹理论进行简化，建立深沟球轴承模型，同样分析了波纹度对轴承振动的影响。Liu等[9-14]基于赫兹理论建立了故障轴承动力学模型，研究了多种故障特征对轴承振动特性的影响。Han等[15]建立转子系统非线性数值仿真模型，也分析了故障对轴承振动特性的影响规律。宋传冲等[16]进一步考虑滚道裂纹的影响，基于非线性赫兹接理论建立转子系统动力学模型，分析了转速和刚度等对系统动力学特性的影响。Tu等[17]考虑轴承滑移时摩擦力的作用，通过建立圆柱滚子轴承打滑振动模型分析轴承的振动特性，但模型同样是基于赫兹接触理论进行建立。

以上文献都是基于赫兹理论建立的轴承动力学模型，从不同角度分析了轴承的振动特性，但在实际运行工况中，轴承各部件之间不可避免会出现滑移现象，而滑移产生的摩擦力和切应力已超出赫兹理论的假设范畴，因此，基于赫兹理论建立的模型并不适用于分析轴承出现滑移的工况。虽然Kaller[18]考虑两接触面摩擦力、相对位移和切应力对接触特性的影响，并提出了非理想赫兹理论，但Kaller的研究只对接触特性进行了分析，并未基于所提出的非理想赫兹理论对轴承振动特性展开深入研究。因此有必要考虑轴承滑移对接触特性的影响，建立动力学模型分析滚动轴承的振动特性。

本文对滑移非理想赫兹进行理论分析，并通过建立局部接触有限元模型获得滚子与滚道的滑移接触指数和接触刚度；基于滑移非理想赫兹系数和刚性套圈假设理论建立考虑滑移接触的滚动轴承动力学模型，对比分析滑移非理想赫兹和理想赫兹接触对轴承振动特性的影响规律。

1 滚动轴承滑移接触理论分析

滚动轴承各部件之间的运动关系极为复杂，当滚子受到的驱动力不足以克服阻力时，滚子与滚道之间的接触面就会产生相对滑移[19]。滚子与滚道的滑移接触会伴随一定的摩擦力和切应力，而理想赫兹理论忽略了接触面之间摩擦力、切应力和相对滑移的影响，因此基于理想赫兹理论分析轴承振动特性会存在一定的影响。为了更准确描述滚动轴承的振动特性，本文基于赫兹理论，考虑滚子与滚道接触面的滑移作用，推导了滑移接触下滚子与滚道的载荷-变形公式。

如图1所示，在外加载荷F的作用下，滚子与滚道相对滑移速度为ω，此时，滚子受到水平向左的牵引摩擦力F1；滚子与滚道发生接触变形后，接触面与x轴之间会形成接触角α，此时滚子在滚道上滑动，滚道接触面为抵抗x方向的挤压变形，对滚子产生一个水平向左的作用力，即滚子受到的切应力。滚子因摩擦力产生的切应力和滚道抵抗挤压变形对滚子切应力的合力设为F2。图1中，滚子与滚道的滑移接触斑区域可以分为滑移区S、接触区H和滑移变形产生的多余接触面积DH。

图1 滑移前后接触斑Fig.1 Contact spots before and after sliding

如图2所示，当轴承在载荷F作用下，滚子与滚道之间存在正方向上的接触应力为σ1；进一步考虑滚子与滚道接触面之间的滑移速度ω时，滚子与外滚道会增加一个斜方向上的应力σ2，其中σ2与滑移接触面垂直；此时考虑滑移接触的总应力为σ3。

图2 滑移接触应力分布Fig.2 Sliding contact stress distribution

纯滚动条件下满足赫兹接触理论，滚子与外滚道之间作用力为F，结合Palmreng公式[20]得出滚子与滚道接触变形为

(1)

式中：l为滚子与滚道的有效接触长度；υ1、υ2为泊松比；E1、E2为滚子与滚道的弹性模量。

由式(1)可知，接触变形与载荷的0.9次方成正比，故滚子与滚道的接触刚度表示为

(2)

结合式(1)、(2)可得出理想赫兹接触下滚子与外滚道接触的载荷计算公式为

(3)

如图3所示，令滚子在水平方向所受到的合力为ΔF，则

图3 滑移接触下载荷-变形Fig.3 Load-deformation of sliding contact

ΔF=F2+F1=F2+μc×F

(4)

式中：F2为滚道对滚子的剪切应力；F1为滚子所受摩擦力；μc为牵引摩擦因数。

在滚子与滚道发生滑移接触时，接触面与x轴形成蠕滑角α，考虑滑移产生附加接触变形量的大小为

(5)

如图3所示，ΔFsin(α)与滑移接触面垂直，同样基于赫兹接触理论可得

(6)

从图3中可以得出在外加载荷F的作用下，滚子与滚道滑移接触的总变形为

(7)

在实际运行工况中，滑移接触角α极小，因此从式(7)中可以看出总接触变形δ3增大，且可近似认为滑移接触下总接触变形δ3与接触面垂直，即滑移接触下滚子与滚道的载荷-变形公式可以用幂指函数表示为

(8)

式(8)中接触刚度和指数均为滑移接触下计算的系数值，其中kh与nh均为考虑滑移接触修正后的滑移接触刚度和滑移指数，与理想赫兹接触下的接触刚度和指数不同，即nh≠n，kh≠k。

2 载荷-位移公式系数修正

通过上述滑移接触的理论分析得出考虑滑移接触下的载荷-变形公式，但上述切应力F2与接触角α无法通过实验测量，所以式(8)中的滑移接触刚度kh和指数nh值无法确定。故本文以NU306圆柱滚子轴承为研究对象，通过建立滚子与滚道的局部接触有限元模型求解滑移接触的变形系数(kh，nh)。NU306轴承的基本参数如表1所示。

表1 NU306轴承参数Tab.1 Parameters of NU306 bearing

2.1 滚子接触有限元模型建立

由于局部滚子接触有限元模型不仅能简化模型的复杂程度，同时能提高模型的计算精度和计算效率，因此本文通过建立局部滚子接触有限元模型替代整体轴承模型计算滑移接触下的kh，nh值。

在实际工况中，外加载荷不足以使轴承发生塑性变形，因此将轴承的材料设置为线弹性材料，材料均为G20Cr2Ni4钢[21]，材料密度ρ=7 810 kg/m3，弹性模量E=206 GPa，泊松比v=0.3。滚子与滚道的接触方式设置为面-面接触；在不考虑润滑条件下，为真实模拟滚子与滚道的接触关系，设置滚子与滚道之间的静摩擦因数为0.15，动摩擦因数为0.02。

如图4所示，滚子与滚道采用SOLID185作为离散实体单元，各节点具有x，y，z三个方向的平移自由度；为保证载荷施加均匀，定义滚子中间截面为刚性壳单元SHELL181，与滚子实体共节点，在滚子中间面施加沿y轴负方向的载荷F同时对滚子设置y方向位移[22]。为实现滚子与滚道之间的相对滑移，在模型中定义轴承外滚道的外径面为刚性壳体单元SHELL181，与滚道外侧面共节点，设置外径面绕z轴逆时针的旋转，实现滚子与滚道的相对滑移。

图4 轴承局部有限元模型Fig.4 Local finite element model of bearing

为确定合适的网格密度，反映滚子与滚道更为准确的接触特性，本文通过对滚子和滚道进行区域网格细化。初始设定单元网格尺寸大小为0.5 mm，按照不同细化等级向滚子与滚道的接触区进行网格逐步细化[23]。通过设置不同网格细化等级对网格进行过渡加密，按照接触区的网格大小分为粗网格、半精网格和精网格，并对计算精度和计算时间进行对比。细化网格参数如表2所示，其中半精网格下滚子和局部滚道的逐步细化网格如图5所示。

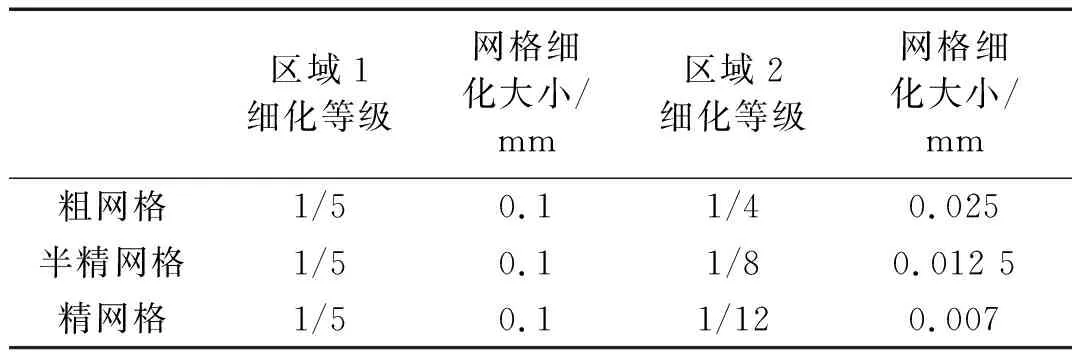
表2 网格细化参数Tab.2 Mesh refinement parameter

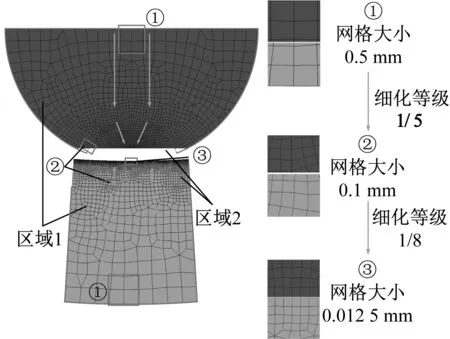
图5 半精网格细化过程Fig.5 Semi-process mesh refinement process

2.2 有限元模型验证与系数修正

基于上述建立的三种不同网格精度的模型，考虑轴承实际运行载荷，设置载荷大小分别为500 N、1 000 N、3 000 N、4 000 N、5 000 N，计算时间设置为0.001 5 s。将设置好的模型分别求解，提取滚子、滚道总接触变形与赫兹理论计算值对比，得出半精网格的计算精度较高，其误差均小于8%，而粗网格计算误差较大，精网格计算时间较长，且精度没有明显升高，综合考虑模型的计算效率和计算精度，故本文采用半精网格进行后续计算。

通过上述施加的载荷，对外径面施加一个绕Z轴顺时针方向的转动，角速度为2 rad/s的相对滑移速度，计算时间同上。为探究不同滑移速度对接触变形的影响，在3 000 N的工况下设置0.5 rad/s，1 rad/s，1.5 rad/s，2.5 rad/s，3 rad/s的滑移转速，计算时间分别设置0.06 s，0.03 s，0.02 s，0.01 s，将设置好的模型导入LS-DYNA中求解。

根据滚子与滚道的运动关系，可得出如图6所示的滑移前后关系图，其中O、A为为滑移前的位置点，O′、A′为滑移后的位置点，通过计算考虑滑移后模型的总接触变形计算为

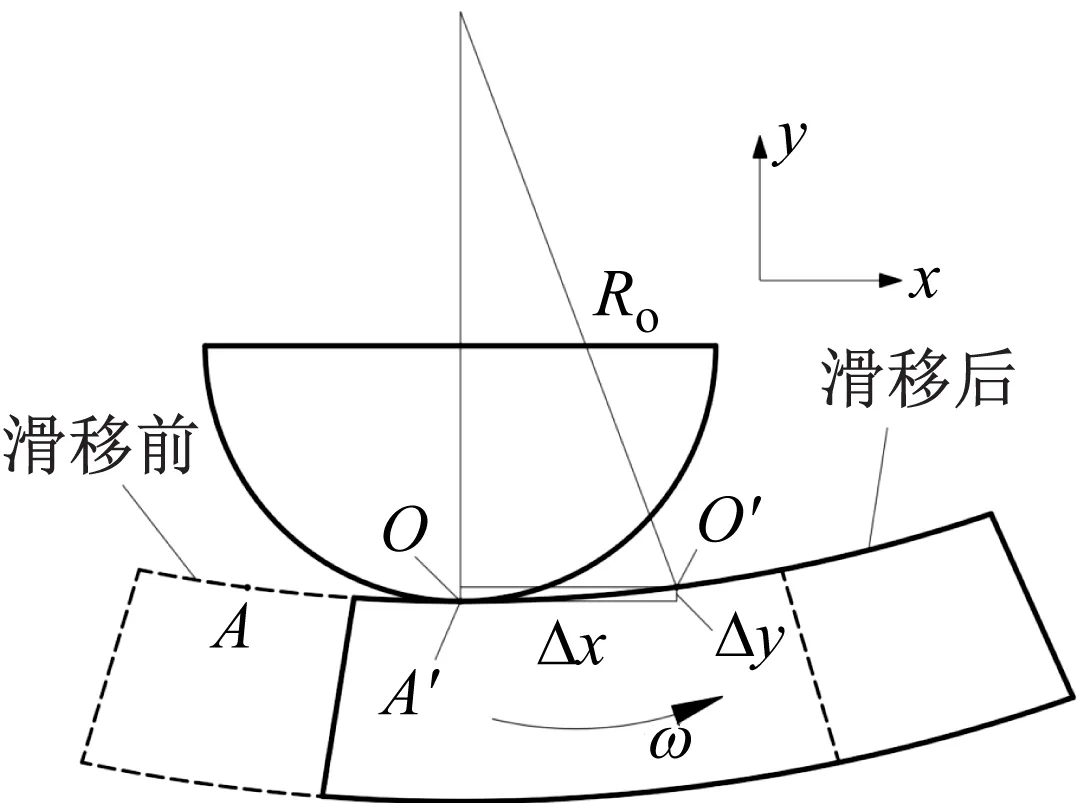
图6 滑移运动位置关系Fig.6 Position relation of sliding motion

δ3=Δy_rolling+Δy_outer-Δy-Pd_FEM

(9)

式中：Δy_rolling、Δy_outer分别为滚子与滚道在y轴负方向的最大变形值；Pd_FEM为初始径向游隙;Δy为考虑滑移后在y方向增加的位移量。

其中Δy可表示为

(10)

式中:Ro为轴承的外滚道半径;Δx为外滚道滑移后x方向的增加的位移量。

通过数据的提取与计算，获得模型接触变形值进行对比，如图7所示。从图7(a)可以观察出考虑滑移接触的变形值大于赫兹理论计算结果，这是由于滚子与滚道的滑移接触产生了摩擦力与切应力作用，导致滚子与滚道之间的接触面增大，故滑移接触下的接触变形大于赫兹接触，与式(7)中分析出δ3>δ1的结果一致；而随载荷增大，滑移接触与赫兹接触的差值增大，是因为载荷增大，滚子与滚道的摩擦力和切应力增大，式(5)中摩擦力和切应力增大会导致接触变形δ2增大，而赫兹理论不考虑相对滑移作用，因此载荷增大，滑移与赫兹接触的差值就增大；同时得出在重载工况，滑移对轴承接触变形的影响更为明显。如图7(b)所示，当外加载荷一定时，不同相对滑移速度对变形值影响较小，即可以忽略不同滑移速度带来的影响。

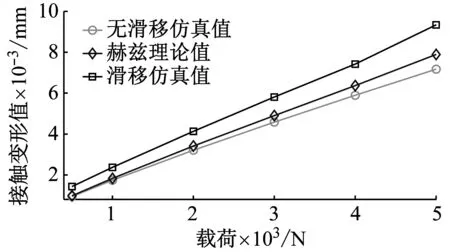
(a) 不同载荷下接触变形

(b) 不同滑移速度下接触变形图7 接触变形对比Fig.7 Comparison of contact deformation

综上所述，赫兹理论忽略了接触面相对滑移的影响，而在实际工况中，滚子与滚道不可避免会发生相对滑移，同时伴随摩擦力和切应力的产生，因此针对轴承振动特性的研究，应该考虑轴承接触面之间相对滑移的作用。

通过对滑移接触的变形值进行幂指函数拟合，可获得载荷-变形公式(8)中的接触系数，其中拟合后的曲线与仿真结果的相似度为99.8%，故用此拟合曲线的系数表示滑移接触刚度kh和滑移指数nh值，如表3所示。考虑到分析对象为圆柱滚子轴承，由文献[24]可知滚子与内、外滚道的载荷-变形公式一致，为缩短计算时间，设滚子和内滚道的载荷-变形系数与外滚道一致。

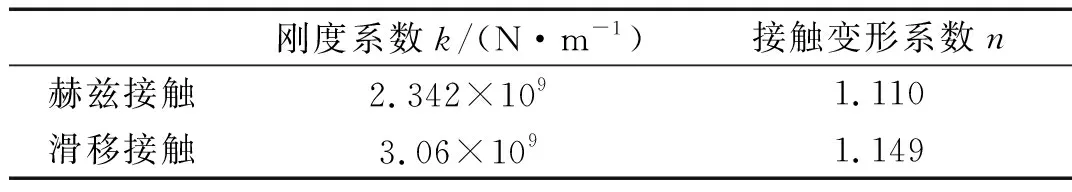
表3 载荷-变形系数Tab.3 Load-deformation coefficient

3 振动特性分析

3.1 滚动轴承动力学模型的建立

为研究滑移接触下滚动轴承的振动特性，本文建立圆柱滚子轴承动力学模型，将滚子与滚道之间接触考虑成弹簧-阻尼系统，如图8所示。其中θj为滚子相对于X轴的位置角,θj表达式为

图8 滚动轴承动力学模型Fig.8 Dynamic model of rolling bearing

(11)

式中:t为时间;ωc为保持架的转速;Nb为滚子数量。

基于刚性套圈假设[25]，圆柱滚子轴承动力学微分方程可表示为

(12)

式中:mi为内圈(含转子)质量;c为油膜阻尼系数;k、n分别表示为滚子与滚道的接触刚度和变形指数(滑移和赫兹接触下的k、n值见表3);Fx、Fy分别表示内圈所受沿X、Y方向的载荷分量;δj为第j个滚子与内外滚道之间的总接触变形。

第j个滚子与内外滚道之间的总接触变形表示为

(13)

式中，Pd为滚子与内、外滚道之间的径向游隙，‘+’表示为括号内的值大于零，否则接触变形值为零。

对于轴承载荷与转速的选择，由文献[26]可知NU306圆柱滚子轴承额定动载荷公式为

P=bmfc(l×cosα)7/9Nb3/4D29/27

(14)

式中:bm为材料的加工系数;fc为形状精度系数；l为滚子有效长度;α为接触角;Nb为滚动体个数;D为滚动体直径。

由上式计算得出轴承的额定动载荷P为47 944.12 N，由经验公式(15)取1 000 N、5 000 N、9 000 N为轴承的轻载、中载与重载工况；同时取1 000 r/min、3 000 r/min、5 000 r/min为轴承的低、中、高速工况，采用四阶定步长Runge-Kutta法对微分方程求解，计算步长设为Δt=1×10-6s。

通过上述动力学模型，计算赫兹接触下转速为1 000 r/min和5 000 r/min时内圈X方向的加速度频域信号，分别得出在79.35 Hz和393.7 Hz处分别出现峰值，与理论公式[27]计算结果基本相符，验证了模型的有效性。

(15)

3.2 滚动轴承振动特性分析

为探究滑移非理想赫兹接触下对轴承振动特性的影响规律，通过对比滑移和赫兹接触下轴承振动信号的均方根值(RMS)和峰-峰值(PTP)，分析载荷、转速对轴承内圈振动信号的影响规律；同时进一步从滑移接触特性的角度分析了不同工况下轴承的振动特性。

表4为内圈X方向振动信号的均方根值(RMS)和峰-峰值(PTP)，从表中可以看出在低、中速工况，滑移接触下轴承振动的RMS值和PTP值大于赫兹理论；但在高速工况，滑移接触振动信号的时域指标值较小；同时在高速工况，RMS和PTP值随载荷增大而减小。即在中、低速工况，赫兹接触下轴承的振动能量小于滑移接触；而在高速工况，赫兹接触下轴承振动能量大于滑移接触，且随载荷的增加，轴承振动能量随之减小。在低、中速工况，轴承内部运行稳定，结合式(8)可以得出考虑滑移接触下滚子与滚道接触变形值增大，接触应力相应增大，故滑移接触下滚子与滚道发生碰撞的振动能量更大；而高速工况，由于阻尼力和滑移接触刚度的共同作用，对轴承内圈的动态效应具有明显的抑制作用，因此，滑移接触下滚动轴承的振动能量较低。

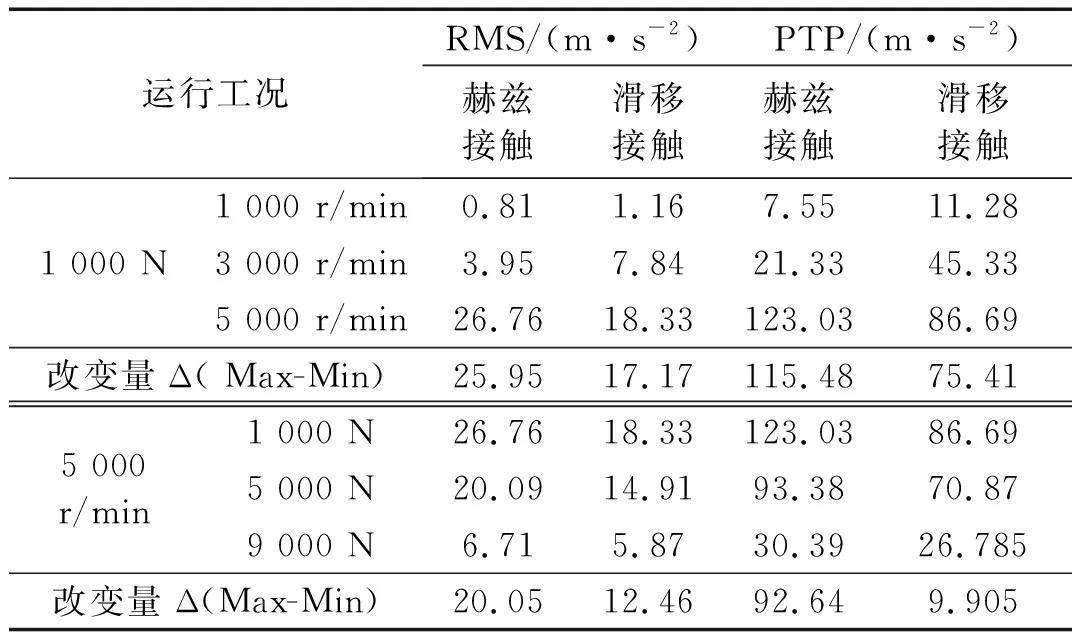
表4 内圈加速度信号RMS和PTP值Tab.4 RMS and PTP value of inner ring acceleration signal

结合表4同样可以观察出，随工况的改变，滑移接触下RMS和PTP的改变量Δ小于赫兹接触，即滑移接触下轴承振动随工况改变的影响较小。滑移接触下的接触刚度kh和接触指数nh增加，这可能是导致滑移接触对工况改变敏感度较低的原因。滑移接触系数实质上是考虑滚子与滚道之间相对滑动，通过理论分析和有限元模型计算获得，从其特征参数不能直观反映滑移接触对轴承振动特性的影响规律，因此为进一步从接触特性的角度分析，针对低速轻载、高速轻载和高速重载三种工况对轴承振动特性进行对比分析。

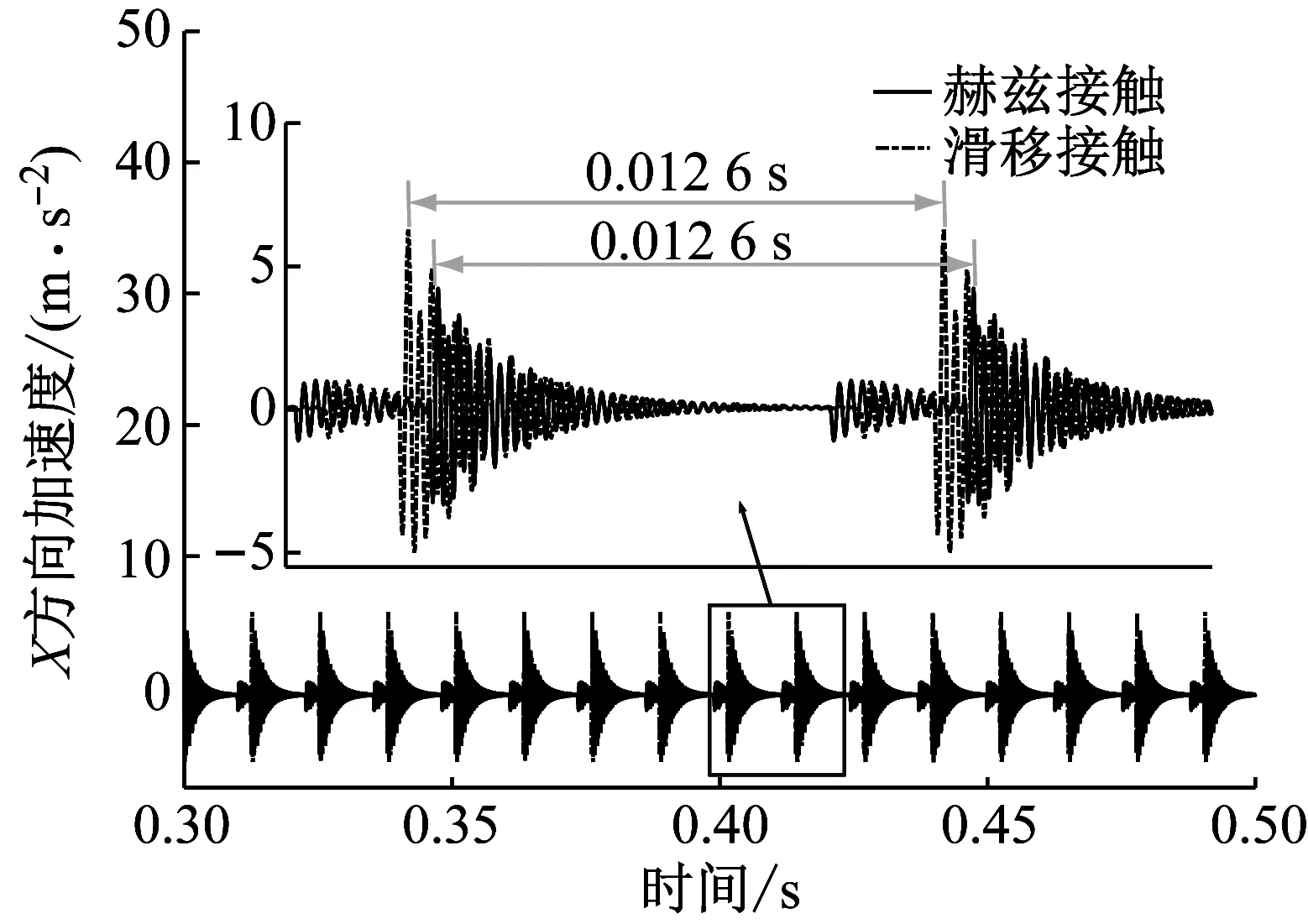
低速轻载工况下,轴承振动信号时、频对比，如图9和10所示。从图9(a)、(b)中可以看出，滑移接触轴承X、Y方向的振动幅值比赫兹接触大，且振动信号存在滞后现象。对振动指标RMS值和PTP值的分析中得出：低速轻载工况，轴承内部运行稳定，滑移接触下轴承振动能量大于赫兹接触，因此，滑移接触下轴承X、Y方向的振动幅值也较大；滑移接触下轴承振动信号滞后的原因是滑移刚度和滑移指数改变，而滑移系数是由于滚子与滚道发生滑移导致，因此，从滑移接触特性的角度可以分析出滚子与滚道的滑移形成的滑移区，即滚子在滑移区与内、外圈发生相对滑动，滚子与滚道接触时间增加，故滑移接触下轴承振动信号会存在滞后现象。图10可以看出，滑移接触下X、Y方向振动信号的频率成分较稳定，进一步说明滚子与滚道发生滑移接触时，接触时间增加，使得内圈与滚子发生碰撞前，存在缓冲区，故滑移接触下内圈的振动信号变得更加平缓。

(a) X方向加速度响应对比

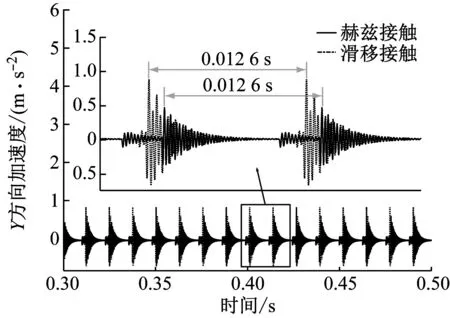
(b) Y方向加速度响应对比图9 1 000 r/min-1 000 N轴承内圈振动响应Fig.9 Vibration response of bearing inner ring of 1 000 r/min-1 000 N

(a) X方向频谱对比

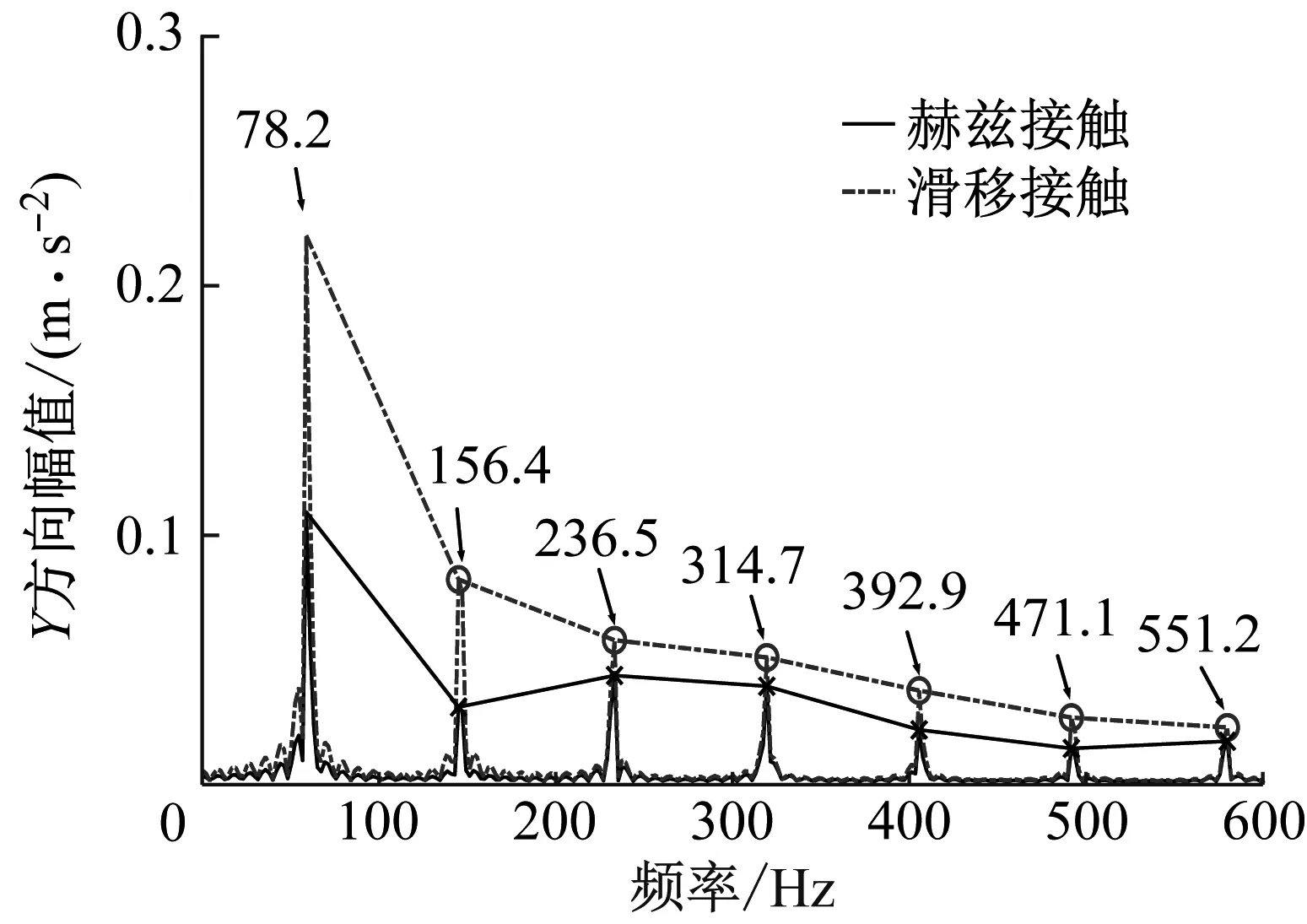
(b) Y方向频谱对比图10 1 000 r/min-1 000 N轴承振动频谱Fig.10 Bearing vibration spectrum of 1 000 r/min-1 000 N

在高速轻载工况中，轴承内圈X、Y方向振动信号的时、频域图对比，如图11和12所示。从图11(a)、(b)可以看出，在高速轻载工况下，赫兹接触的振动信号的幅值比滑移接触大，且滑移接触产生的信号滞后现象并不明显。在高速工况中，由于油膜阻尼力、滑移刚度、惯性力等作用，对轴承动态效应的抑制效果增强，故滑移接触下振动信号幅值较弱。从接触角度分析，滚子公转转速增加，滚子经过滑移区的时间明显缩短，因此滑移接触下振动信号的滞后时间明显缩短。图12(a)、(b)中可以看出在中低频段，赫兹接触频率衰减速度明显比滑移接触快，进一步说明考虑滑移接触下的内圈振动信号会更稳定，且衰减程度更平缓。对比图12与图10中轴承振动幅值，可以看出高速工况下，轴承振动信号幅值较大，这是由于轴承在低速轻载工况下运行较稳定，当内圈转速为5 000 r/min时，轴承的动态特性会明显增强，故高速工况下轴承X、Y方向振动幅值更大。

(a) X方向加速度响应对比

(b) Y方向加速度响应对比图11 5 000 r/min-1 000 N轴承内圈振动响应Fig.11 Vibration response of bearing inner ring of 5 000 r/min-1 000 N

(a) X方向频谱对比

(b) Y方向频谱对比图12 5 000 r/min-1 000 N轴承振动频谱Fig.12 Bearing vibration spectrum of 5 000 r/min-1 000 N

高速重载工况下轴承振动信号的时、频域对比，如图13、图14所示。从图13可以看出，滑移接触下轴承X、Y方向振动信号幅值较小，同时存在明显滞后现象。考虑到在高速重载工况中轴承运动特性复杂，滑移接触刚度对滚动轴承内圈运动的抑制效果明显，故滑移接触下轴承内圈X、Y方向上的振动信号幅值较低；同时由于外加载荷增大，滚子与滚道接触斑面积增大，滚子经过滑移区时间会明显增加，因此，滚子与滚道发生碰撞的振动信号会出现明显滞后现象。从图14(a)、(b)可以看出X、Y方向的振动频率成分不稳定，这是由于高速重载工况下，轴承各部件的运动状态更为复杂，使得轴承内圈在X、Y方向上的动态特性趋向不稳定。对比图12与图14，可以看出高速重载工况中，轴承内圈X、Y方向的振动信号幅值有明显降低，这是由于转速相同，外加载荷增加使得轴承内部的动态效应减弱，故重载工况下的内圈振动幅值较低。

(a) X方向加速度响应对比

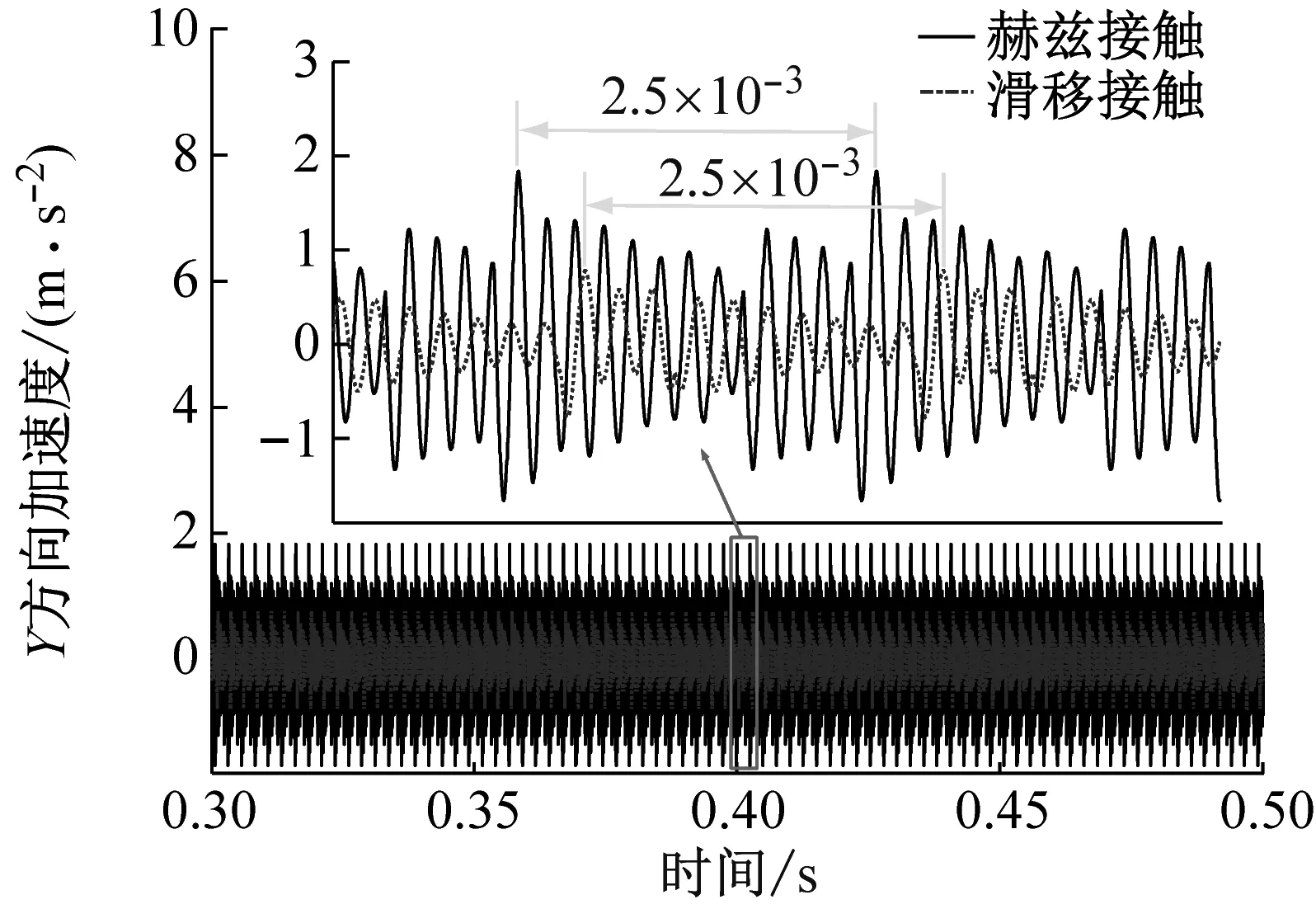
(b) Y方向加速度响应对比图13 5 000 r/min-9 000 N轴承内圈振动响应Fig.13 Vibration response of bearing inner ring of 5 000 r/min-9 000 N

(a) X方向频谱对比

(b) Y方向频谱对比图14 5 000 r/min-9 000 N轴承振动频谱Fig.14 Bearing vibration spectrum of 5 000 r/min-9 000 N

5 结 论

本文以NU306圆柱滚子轴承为研究对象，从理论上分析滚子与滚道的滑移接触特性，并推导了滑移非理想赫兹接触下的载荷-变形公式。以ANSYS中LS-DYNA为平台，获得滑移接触下的接触刚度和变形指数，并通过建立滚动轴承动力学模型，对比分析了不同工况滑移接触和赫兹接触下轴承的振动特性，主要结论如下：

(1) 滑移接触下，滚子与滚道之间存在摩擦力与切应力的作用，滚子与滚道接触面增大，故接触变形大于理想赫兹接触下的接触变形，且在重载工况，与赫兹接触的变形值偏差更为明显。

(2) 在中低速工况，滑移接触引起的变形更大，滚子与滚道之间接触力增大，故轴承的振动冲击能量要大于赫兹接触；而在高速工况，由于刚度和阻尼力等作用，滑移接触下轴承振动信号的幅值和能量较低。

(3) 在低速轻载工况，滑移接触存在滑移区，轴承振动信号存在滞后现象，而随转速升高，滚子经过滑移区时间缩短，振动信号滞后现象减弱；而在重载工况，接触斑增大，滚子在接触区时间增加，滑移接触下振动信号存在明显滞后。

(4) 考虑滑移非理想赫兹接触对轴承振动特性的研究与理想赫兹接触存在明显的差异，滑移非理想赫兹接触进一步考虑接触面间相对滑移的作用，与实际工况更贴近。