分数阶非线性隔振系统的超谐波共振与周期运动转迁规律分析

屈鸣鹤， 吴少培， 俞力洋， 丁旺才， 李国芳， 黄 然

(兰州交通大学 机电工程学院，兰州 730070)

黏弹性隔振元件被广泛应用于机械设备中，如航空器的辅助动力装置隔振器[1]、轨道车辆二系悬挂的橡胶堆、汽车底盘中的悬架缓冲块[2]、机床的减震垫等。其中橡胶只有在变形较小时才可近似看作线性弹性材料，超出这个范围表现为非线性弹性。由于其特殊的结构可以同时表现出黏弹性，能集缓冲、隔振、降噪等功能于一身，并且可根据实际需要来设计外形、刚度及阻尼[3]。为了更好地描述黏弹性隔振系统的力学特性，有学者提出三元件固体整数阶模型，可以更好地反映黏弹性材料的松弛和蠕变特性[4]。学者们将可以等效橡胶材料的三参数力学模型称为Zener模型和Ruzicka模型[5-7]。

分数阶微积分由于缺乏实际应用背景使其长期以来没有得到研究和发展，近几年分数阶微积分的定义、特性和计算才得以在工程领域应用[8]。虽然传统的整数阶模型可以描述橡胶材料的力学特性，但不足以描述黏弹材料的频率相关性。分数阶力学模型可以对黏弹性加以修正，进而将整数阶模型优化为分数阶模型描述材料的本构关系[9]。罗文波等[10]为准确描述沥青混合料的动态黏弹性力学行为，在分数阶Zener模型的基础上提出了改进的分数阶Zener模型。Martin等[11]对黏弹性纳米梁的分数阶动力学行为进行研究，借助拉普拉斯变换等方法对黏弹性特性进行了研究分析。Bratu等[12]通过分数阶Zener模型描述了道路的复合土结构，并分析了系统的动态响应。Lewandowski等[13]用分数阶Zener模型来反应材料的流变特性。Ciniello等[14]分析了温度对黏弹性材料的影响。

针对隔振系统的非线性特性，常宇健等[15]提出一种含有分数阶微分的金属橡胶黏弹性本构模型，在此基础上建立了非线性动力学模型，并结合实验验证了模型的准确性。秦浩等对Caputo定义下的分数阶Duffing振子解析解和数值解的比较，验证了分数阶项化简为一阶三角函数形式系统产生分岔和混沌的必要条件。孔凡等[16]通过谐波平衡法研究了简谐激励下同时具有滞回特性和分数阶阻尼单元系统的稳态响应，采用不同方法求解系统的迟滞回线，发现谐波平衡法与逐步积分法得到的相关结果吻合较好。Zhen等[17]通过高次谐波平衡法求解了含负刚度几何非线性系统的动力学响应，并对其隔振性能进行了分析。余慧杰等[18]通过三次非线性函数描述金属橡胶的非线性特性，用分数阶模型描述其黏弹性，所建立的分数阶非线性模型可以更加准确描述橡胶动态特性。

由于恢复力包含三次方非线性项，系统的动力学响应更加复杂，低频区甚至存在超谐波共振。零部件的疲劳破坏与不同频率的幅值相关，忽略低频的幅值会对零部件的疲劳寿命设计带来误差[19]。对于隔振系统而言，准确预测每个频带区间的动力学响应是有必要的。精密仪器设备经常处于低频微幅的振动环境中，金属橡胶隔振器是一种广泛应用于微振动隔离的装置[20-22]。随着激励频率改变，系统的动力学响应也会发生变化，甚至出现分岔和混沌，进而影响了系统的稳定性，对系统的隔振性能以及疲劳寿命预测带来影响。非线性系统还存在周期运动多样性，运动转迁过程更加复杂，甚至存在多态共存现象，这影响了低频区隔振系统动力学响应的准确预测。针对整数阶非线性系统的动态特性研究已相对成熟，而分数阶非线性系统的周期运动多样性及转迁规律有待揭示[23-26]。

为了揭示分数阶非线性隔振系统的动力学响应，本文对系统的超谐波共振和周期运动多样性研究分析。首先对分数阶项进行化简处理，其次采用高阶谐波平衡法求解系统的稳态响应，数值仿真系统的动力学性能并对近似解析结果进行比较。接着建立两个Poincaré映射描述系统周期运动的多样性及周期运动的转迁规律，采用Floquet理论对分岔类型加以判定。最后对超谐波共振和周期运动多样性之间的关系分析研究，进一步揭示系统参数对幅频特性、分岔及混沌的影响。

1 模型建立及响应求解

1.1 分数阶非线性Zener模型建立及分数阶项处理

采用分数阶非线性Zener模型描述橡胶的黏弹性如图1所示，其中M为系统的质量；F为外激励幅值；X1为质量块的位移；X2为节点的位移；Ω为外激励频率；K1为线性弹性恢复力刚度系数；C为黏性阻尼系数；FK为三次非线性弹性恢复力；D为分数阶微分项；K为分数阶项的系数。引入外激励幅值F的对照参数进Fs，进行如下变量代换

图1 分数阶非线性Zener模型Fig.1 Fractional nonlinear Zener model

分数阶非线性Zener模型无量纲微分方程为

(1)

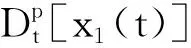
(2)

Γ(y+1)=yΓ(y)

(3)

式中,Γ(n)为Gamma函数，满足式(3)。设质量块的稳态响应为

(4)

将式(4)代入式(2)并引入文献[24]中的公式

(5a)

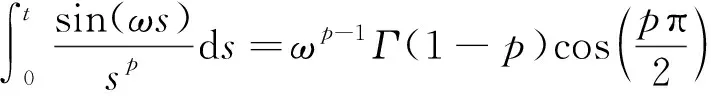
(5b)

取分数阶项的一阶近似化简可得

(6)

式(6)所得分数阶项不仅具有阻尼作用也具有刚度作用与很多文献结果相同，其中文献[16]通过参数识别验证了分数阶项采用一阶三角函数表示在实际工程应用的合理性。本文主要研究隔振系统高次谐波幅值相比基波幅值是小量的情况，进而分数阶化简忽略高阶项，只取一阶近似。

1.2 等效线性刚度系数和等效阻尼系数分析

将分数阶项化简所得一阶三角函数式(6)代入到式(1)中，系统的无量纲微分方程变为

βx1(t)]=fcos(ωt)

(7)

系统等效线性刚度系数Keq和等效阻尼系数Ceq为

(8)

(9)

由式(8)和式(9)可知，分数阶的系数λ、分数阶的阶数p对等效线性刚度系数Keq和等效阻尼系数Ceq都有一定影响。下面对系统的等效线性刚度系数Keq和等效阻尼系数Ceq进行研究。选取系统结构参数ξ=0.1，μk=2，ε=0.2，f=5，取分数阶的阶数p=0.5。由图2(a)可以看出分数阶系数λ越大，等效线性刚度系数Keq越大，且随频率ω的增大而增大。分数阶系数λ越小，等效阻尼系数Ceq越小，且随频率ω的增大在低频区快速减小，离开低频区等效阻尼系数Ceq无明显变化。其次取分数阶系数λ=0.01，由图2(b)可以看出频率较小时，分数阶项的阶数p越小，等效线性刚度系数Keq越大；而频率ω较大时，分数阶的阶数p越小，等效线性刚度系数Keq越小；等效线性刚度系数Keq随着频率ω增大而增大。在超低频区，分数阶的阶数p越小，等效阻尼系数Ceq越大；离开超低频区，分数阶的阶数p越大，等效阻尼系数Ceq越大。在低频区等效阻尼系数Ceq随着频率ω的增大迅速减小，随着频率ω继续增大离开低频区，等效阻尼系数Ceq无明显变化。

(a) 系数λ与等效线性刚度系数和等效阻尼系数的关系

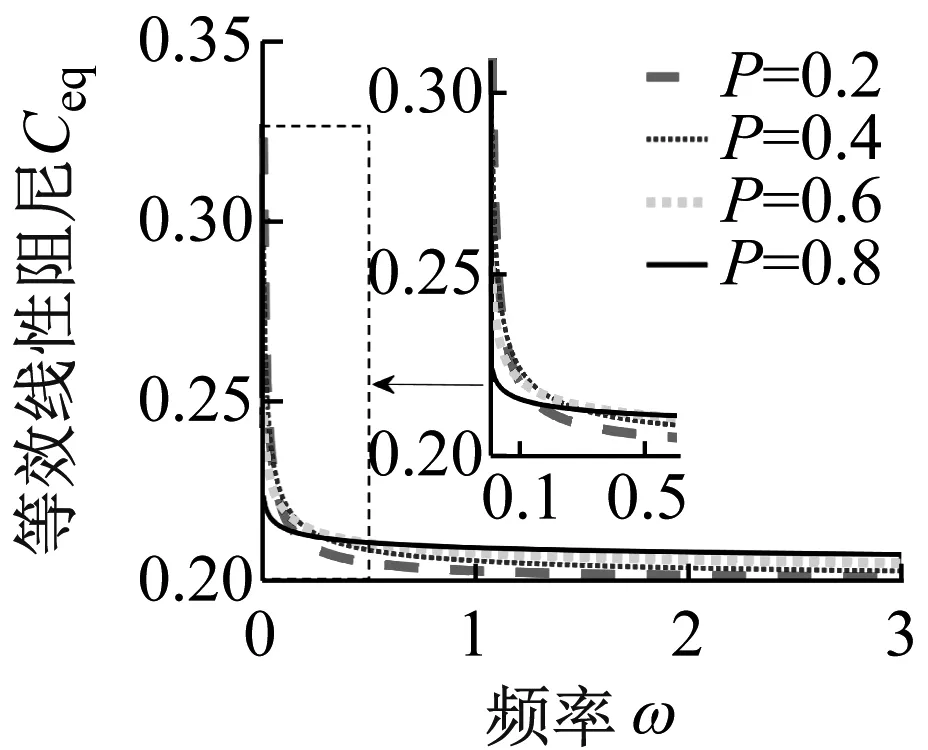
(b) 阶数p与等效线性刚度系数和等效阻尼系数的关系图2 分数阶项与等效线性刚度系数和阻尼系数的关系Fig.2 Relationship between fractional order term and equivalent linear stiffness and damping

不同分数阶的系数λ和分数阶的阶数p会改变系统的等效阻尼系数Ceq和等效线性刚度系数Keq，进而会改变系统的固有频率。

1.3 谐波平衡法求解系统稳态响应

设节点的稳态响应为

(10)

其中(2n-1)表示高阶谐波的阶次。当n=1时根据式(4)和式(10)可得质量块和节点的一阶谐波响应为

x1=A1cos(ωt)+B1sin(ωt)=A11sin(ωt+θ1)

(11a)

x2=a1cos(ωt)+b1sin(ωt)=a11sin(ωt+φ1)

(11b)

将式(11)代入到式(1)中进行一阶谐波平衡，可得质量块与节点幅值和相位的关系

(12)

将式(12)代入到式(11a)中可得到质量块的一阶稳态响应

(13)

将式(13)和式(11b)代入式(7)可得

(14)

(15)

进而可以求解出节点的一阶幅值与相位

根据以上方法获取的水体信息如图1所示，同时根据Landsat OLI成像的准确时间，借助于磨盘山水库同一时间的水文观测资料、水库水位和流量等水文数据，基于库容曲线计算出当时的库区水面面积值为22.012 km2，并将不同方法所获取的水库面积与实测值进行对比，如表1所示。

(16)

(17)

系统的高次超谐波响应需先求解节点处的各阶谐波幅值系数，再选取时间历程图中节点的最大位移作为幅值，进而得到质量块的高次响应。当n=2时采用三阶谐波平衡法设节点处的响应为

(18)

对式(18)进行三阶谐波平衡可得如下方程组。

(19a)

(19b)

(19c)

36εω3a1b1b3ξ3-30εω2a1a3b1ξ2-3εωa1b1b3ξ+

(19d)

系统参数确定的条件下借助计算机求解并对结果进行数据处理，即可得到节点幅值系数a1、b1、a3、b3的值[17]，再将节点幅值系数代入式(1)可得质量块的幅值系数

(20)

进而得到质量块的三次稳态响应。

(21)

根据三阶谐波平衡法的求解过程以此类推可得系统的高次谐波响应。

1.4 数值方法对比

随机选取一组系统参数：μk=0.5，f=5，ξ=0.1，ε=0.1，λ=0.1。采用四阶Runge-Kutta法对系统数值求解，通过动力学仿真软件UM对隔振系统进行虚拟实验仿真，不同方法求解系统动力学响应结果接近，如图3所示。

(a) 质量块瞬态响应

(b) 质量块稳态响应图3 质量块时间历程图Fig.3 Time history diagram of mass block

一阶谐波平衡法只能求解系统的主共振，无法求解系统的超谐波共振，为进一步研究系统在低频区的动力学响应，采用三阶谐波平衡法对系统进行求解进而得到超谐波共振如图4所示。

图4 不同方法求解系统的幅频响应曲线Fig.4 Amplitude-frequency response curve by different methods

2 系统运动状态与分岔类型

3 超谐波共振下的周期运动多样性

为方便描述系统运动规律，定义符号T-N来描述系统的运动状态，其中T为系统运动的周期数，N为周期运动内简谐振动的次数。为避免混沌出现，选取阻尼系数相对较大的基准参数：μk=0.15，ε=0.6，p=0.5，λ=0.1，f=5，ξ=0.5。选取n=5采用高阶谐波平衡法可得系统质量块的幅频曲线如图5所示。

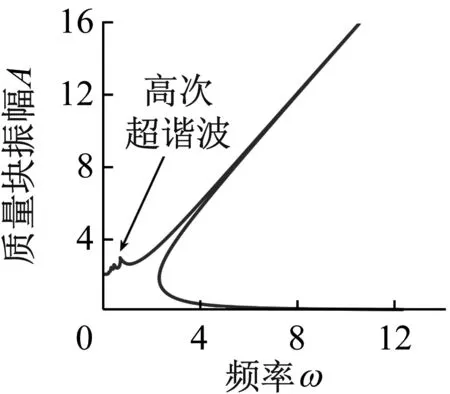
(a) 主共振及超谐波共振

(b) 超谐波共振局部放大图图5 幅频特性曲线图Fig.5 Amplitude-frequency response curve

从图5中可见高次超谐波共振幅值相比较主共振幅值非常小，但是在扫频的过程中高次超谐波也存在跳跃现象如图5(b)所示，系统在低频区也存在多态共存现象且动力学行为更加复杂。随着激励频率改变，系统的动力学响应出现分岔和混沌，这影响了隔振系统的稳定性，对系统的动力学响应预测带来影响。随着频率ω的降低，数值模拟系统的运动状态规律：1-1→1-2→1-1→1-3→1-5→1-7→1-9，如图6所示。

(a) 定相位面

(b) 定极大位移面图6 系统质量块的运动状态Fig.6 Motion state of system mass block

对比超谐波共振的阶次可见超谐波共振的阶次越高，周期运动内的简谐振动次数越多，周期运动内简谐振动的次数与超谐波共振的阶次近似一致。随着超谐波次数的增加，幅频曲线跳跃的距离减小且跳跃方向与分岔图中SNB突变的方向一致。由于设解的形式均为奇数次谐波，无论谐波平衡法设其解的阶次为多大，该方法都具有一定局限性。从图7相图可以看到在ω<1的低频区，随着频率ω减小系统始终保持周期一运动，但是周期内的简谐振动次数增加。

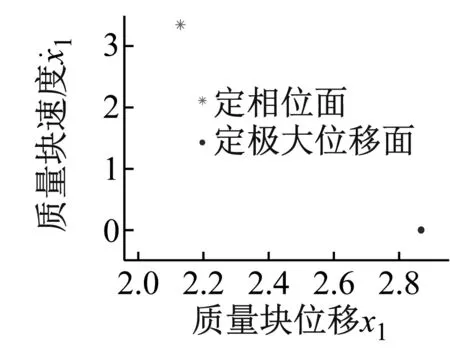
(a) ω=1的Poincaré截面图和相图(1-1运动)

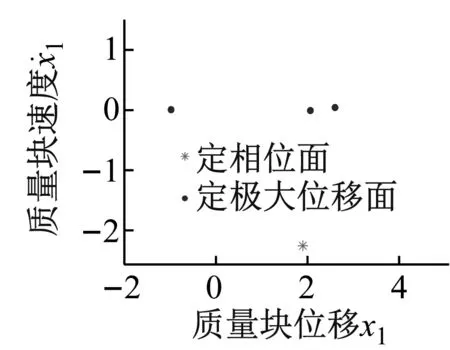
(b) ω=0.696 1的Poincaré截面图和相图(1-3运动)

(c) ω=0.440 6的Poincaré截面图和相图(1-5运动)

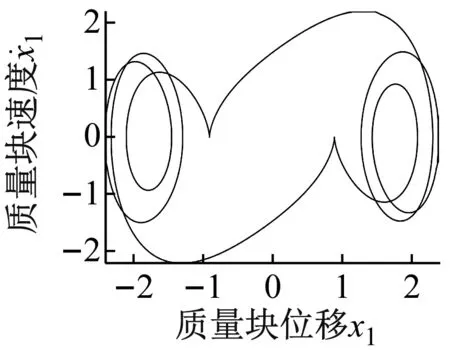
(d) ω=0.328 6的Poincaré截面图和相图(1-7运动)

(e) ω=0.230 6的Poincaré截面图和相图(1-9运动)图7 系统的Poincaré截面图和相图Fig.7 Poincaré section diagram and phase diagram of the system

由于Duffing系统的恢复力为奇函数，这也导致系统的运动状态在相图中也呈现为反对称的运动轨迹，运动状态及运动转迁过程更加复杂。

4 分数阶项对超谐共振及周期运动转迁的影响

下面主要研究分数阶微分项的系数λ和阶数p对系统超谐波共振和周期运动转迁的影响，选取n=5采用高阶谐波平衡法求解系统响应，数值仿真系统动力学响应。

首先分析分数阶系数λ对超谐波共振的影响，选取基准参数为：μk=0.15，ε=0.6，f=5，ξ=0.01，取分数阶的阶数p=0.5，分数阶系数分别取λ=0.1、λ=0.2、λ=0.3，系统在低频区的超谐波共振如图8(a)所示。由于分数阶项不仅具有阻尼作用也具有刚度作用，进而随着分数阶系数λ增大，超谐波共振的幅值与弯曲程度减小。当分数阶系数继续增大到λ=0.3时，9次超谐波共振消失，可见较大的分数阶系数λ不仅可以有效降低超谐波共振的幅值，还可以抑制高次超谐波共振的出现。

(a) 不同分数阶的系数λ

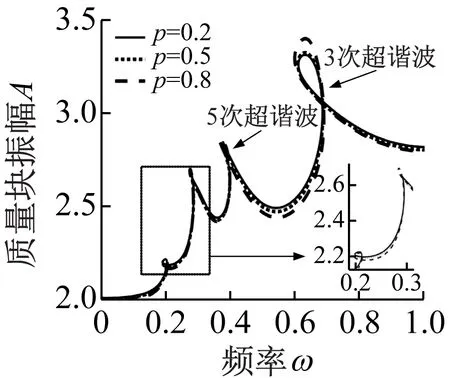
(b) 不同分数阶的阶数p图8 超谐波共振幅频曲线图Fig.8 Super harmonic resonance amplitude frequency characteristic curve

其次分析分数阶的不同阶数p对系统超谐波共振的影响。选取基本参数为μk=0.15，ε=0.6，f=5，ξ=0.01，分数阶系数取λ=0.1，分数阶的阶数分别取p=0.2、p=0.5、p=0.8，系统在低频区的超谐波共振如图8(b)所示。从图8(b)可见在频率ω<0.3的局部放大图中，分数阶的阶数p越小，7、9次超谐波共振的峰值越大；当频率ω>0.3时，3、5次超谐波共振的峰值随阶数p的增加而增高。

接着研究分数阶系数λ对系统周期运动转迁的影响。数值仿真得到不同分数阶系数λ所对应系统质量块的分岔图如图9所示，虚线表示系统发生鞍结分岔SNB。从图9可见分数阶系数λ由0.1增加到0.2时，分岔图中的SNB的个数由4减小为1并且3次超谐波和5次超谐波转迁过程中的混沌消失；随着分数阶系数λ继续增加为0.3时，鞍结分岔SNB也消失。可见分数阶系数λ的增大还可有效避免系统出现分岔和混沌。

(a) λ=0.1的频率正扫分岔图和频率反扫分岔图

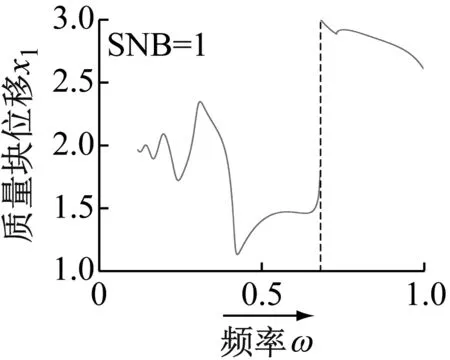
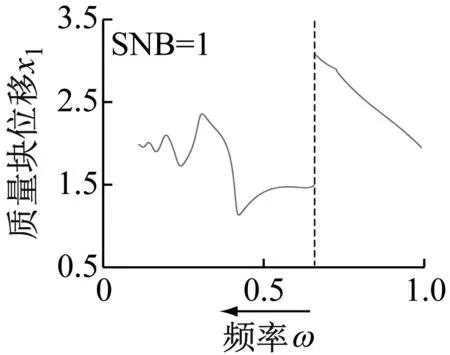
(b) λ=0.2的频率正扫分岔图和频率反扫分岔图

(c) λ=0.3的频率正扫分岔图和频率反扫分岔图图9 不同分数阶系数对应质量块的分岔图Fig.9 Bifurcation diagram of mass block corresponding to different fractional order coefficients

其次研究分数阶的不同阶数p对系统周期运动转迁规律的影响如图10所示，虚线表示系统发生鞍结分岔SNB。当分数阶的阶数p由0.2增加为0.5时，SNB的个数由5减小为4，在频率ω=0.234 2的SNB消失，在频率ω=0.31处的混沌消失；随着分数阶的阶数p继续增加为0.8时，SNB的个数由4又增加为5，在频率ω=0.234 2处再次出现SNB，可见在本节基准参数下为有效抑制在超低频区出现分岔和混沌，分数阶的阶数p应取值适中。

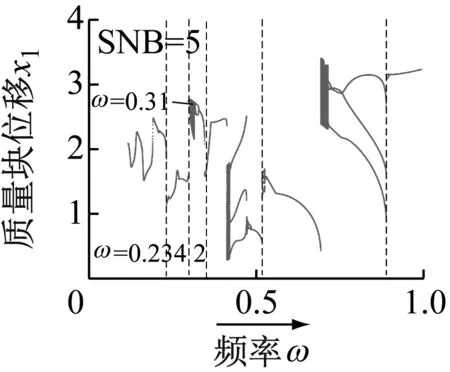
(a) p=0.2的频率正扫分岔图和频率反扫分岔图

(b) p=0.5的频率正扫分岔图和频率反扫分岔图

对比幅频曲线和分岔图可见在相邻次数超谐波共振的转迁过渡区存在混沌，并且存在多态共存现象。为进一步确定多态共存下的运动状态及转迁规律，在本节选取基准参数下，选取分数阶的系数λ=0.1和分数阶的阶数p=0.5，系统多态共存区域主要分布在主共振和3次超谐波共振转迁过渡区，以及3次超谐波共振和5次超谐波共振转迁过渡区，系统运动状态的多样性如图11所示。

图11 多态共存及其相邻区域分岔图Fig.11 Multi state coexistence and its adjacent region bifurcation diagram

由于系统存在SNB、倍周期分岔(PDB)、叉式分岔(PFB)以及边界激变(BC)等多种分岔，在这些分岔的诱导下甚至会出现混沌，并且该过程不可逆，具体转迁规律如图12所示。

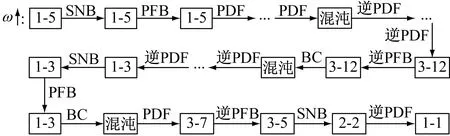
图12 多态共存及相邻区域运动转迁规律Fig.12 Multi state coexistence and movement transition law of adjacent regions

在橡胶工业中，可根据上述规律选择恰当的系统参数，进而避免隔振系统动力学响应出现非线性跳跃现象以及分岔和混沌，使橡胶隔振系统的动力学性能更佳。

5 结 论

本文采用分数阶非线性Zener模型描述黏弹性隔振系统，采用高阶谐波平衡法求解了系统的稳态响应并结合多种方法对结果进行比较，阐述了低频区系统幅频特性与周期运动多样性之间的关系，研究了分数阶项对中低频范围内隔振系统的分岔、混沌和多态共存等复杂非线性动力学行为的影响，得出以下结论：

(1) 针对系统在低频区域的超谐波共振，分岔图中出现鞍结分岔SNB对应的频率与幅频曲线发生跳跃的频率一致，鞍结分岔SNB突变的距离随谐波次数增加而减小。

(2) 分数阶系数λ的增大不仅可有效降低超谐波共振的峰值，还可有效避免系统发生分岔和混沌。

(3) 相邻次数超谐波共振转迁过程中存在多态共存的现象，转迁过程中相继出现PFB、SNB、PDF和BC等多种分岔类型，在分岔诱导下甚至会出现混沌且该过程不可逆。

上述研究结果与方法可为高次谐波为小量的隔振系统在微振动下的动力学响应预测提供一定理论依据。