考虑分层梯度的筒状蜂窝基座隔振性能研究

黄江成， 肖正明， 刘 涛， 刘卫标

(1.昆明理工大学 机电工程学院，昆明 650500；2.云南昆钢重型装备制造集团有限公司，昆明 650501)

振动不仅会影响机械设备本身的精度和使用寿命，甚至使零件损坏，也会传递给周围的设备，使之产生振动无法工作，所以，有效地采用隔振技术是现代工业的前沿课题。传统的船舶设备隔振大都采用弹簧或者橡胶制作而成，一般为线性隔振系统，这些用作隔振缺点比较明显，包括：加工制造较复杂、价格昂贵、承载能力差、寿命较短易老化等。近年来，蜂窝结构凭借其高孔隙率、低密度的特点，能够满足隔振、轻量化要求[1],为船舶设备隔振基座设计提供了新思路。

针对蜂窝结构的隔振抗冲击性能，国内外专家学者们展开了广泛的讨论与研究。Banerjee等[2]以普通六边形蜂窝结构为例，借用等效连续介质模型分析了其自由振动特性。Hayes等[3]运用微极理论分析了正六角形蜂窝的谐响应情况以及变形情况。Valeev[4]致力于振动隔离的准零刚度超材料的研究，利用准零刚度系统原理，可以获得低自然频率和高隔振效果。Liu等[5]提出的具有智能开关力学性能和隔振效果的零泊松比超材料，使用形状记忆的4D打印方法制备，可以感知温度变化和调节机械性能。张相闻等[6-7]提出了一种可控可调胞元参数的抗冲击隔振蜂窝基座，综合考虑了抗冲击、隔振性能进行胞元参数优化设计,该基座在中高频段隔振效果显著。秦浩星等[8-9]通过引入周期声学超材料结构，并建立声子晶体蜂窝基座动力学模型，研究了其局域减振规律，结果表明声子晶体的引入使得蜂窝基座隔振性能大幅度提升。上述研究主要基于均匀胞元参数的增加或减少对隔振性能的影响，对其胞元参数进行了匀质单目标的优化设计，其次设计的基座类型多为规则方形，易出现基座结构应力集中现象以及牺牲了基座面内刚度来获得较高的隔振性能。

基于梯度材料的概念，梯度蜂窝材料在受到面内冲击载荷时，其内部微结构的梯度设计可实现对变形模式和应力应变曲线的可控、可调。刘颖等[10]通过分层梯度递变模型,探讨了梯度变化控制蜂窝材料动态能量吸收特性。吴鹤翔等[11]研究了屈服强度梯度变化和冲击载荷对蜂窝结构的抗冲击性能的影响。李谱等[12]研究了厚度梯度箭形负泊松比蜂窝基座在瞬态冲击载荷下的动态性能，结果表明基座的厚度梯度设计有利于提升其抗冲击特性。李坚等[13]考虑分层密度梯度，研究蜂窝材料面内动态压缩及吸能特性。Li等[14-15]基于典型拉胀材料，探讨了梯度设计对蜂窝夹层板以及环状胞元结构的声振性能的影响。Ajdari等[16-17]也运用了结构分层梯度的概念，利用分层梯度带来的性能优势，对蜂窝结构进行了性能提升。学者们在蜂窝结构静力学性能控制方面、准静态或强制位移加载变形方面，传声控制以及瞬态爆炸冲击响应情况等方面，均进行了相关研究并取得了不错的进展。但是，目前蜂窝结构隔振性能的研究大都停留在均匀参数的基础上，对于蜂窝结构分层梯度变化与隔振性能之间的联系尚需系统地建立，分层梯度的蜂窝结构在隔振基座的应用还需要进一步分析讨论。

综上所述，本文提出了一种圆筒状蜂窝基座，对比分析了圆筒状蜂窝基座与方形蜂窝基座抗变形承载能力。通过OptiStruct内置的序列二次规划算法，以振级落差和极限屈服应力为约束条件，最小质量为目标函数，优化出了圆筒状蜂窝基座最佳的壁厚，内凹角度参数。在优化得出的均匀胞元参数的基础上，分别以胞元壁厚和胞元内凹角度为设计变量，对蜂窝基座进行了厚度梯度，角度梯度设计，分别探讨了两种梯度设计对其隔振性能的影响。以期建立蜂窝结构隔振性能与胞元分层梯度之间的联系，旨在为隔振蜂窝基座设计提供参考。

1 筒状蜂窝基座结构性能分析及评价指标

1.1 筒状蜂窝基座结构参数

综合考虑隔振基座的强度、质量和隔振性能，内六角蜂窝型轻量化隔振基座具有较好的减振性能，且强度合格，质量轻，加工制造难度相对低，应用面广，更适合工程实际应用，因此本文提出的圆筒状蜂窝隔振基座内部蜂窝芯选用内凹六边形胞元。胞元相关参数定义为宽度B，高度H，壁厚t，内凹角度θ，内凹肋杆l，如图1所示。蜂窝基座内部采用纵向排列的胞元，横向依次圆环形周期排列，如图2所示。实际工程应用尺寸取决于设备(振源)振动频率，设备大小及质量，基座安装空间等因素。在初始设计中，以船舶典型设备基座尺寸为参考，基座高度为300 mm，圆筒外径为420 mm，内径为360 mm。纵向设计6层蜂窝芯胞元，胞元形状为内凹等高度可闭合内六角蜂窝(胞元形态比B/l=2，2lcosθ=const)。内凹角变化范围为[-45°，0°]，在此范围凹角大小与胞元泊松比及隔振性能影响关系较明显。

圆筒状蜂窝基座固定于板架，基座上方安装机械设备(振源)，板架长1 800 mm，宽1 000 mm，板厚6 mm，板架纵骨用T型材TN50×50×5×5，肋骨用等边角钢 L30×3，扶强材用T型材TN25×25×3×3，板架参数与张相闻等的一致。由于在实际仿真过程中，机械设备与螺栓并不是研究的重点，所以有限元模型对螺栓与设备进行了简化处理。整个减振系统如图3所示，设备质量为300 kg，用质量点代替，重心相对于基座上面板高度为200 mm，质量点与基座上面板选择MPC连接模拟，板架和蜂窝基座均采用高强结构钢，弹性模量为210 GPa，密度为7 800 kg/m3，泊松比为0.3，板架四周简支。

图3 圆筒状蜂窝基座减振系统Fig.3 Cylindrical honeycomb base damping system

1.2 有限元模型可靠性分析

为了验证有限元模型的可靠性，本文建立了与文献[18]参数相同的计算模型。设置相同的频响分析步骤，然后提取了蜂窝隔振基座的一阶垂向模态。有限元模型的一阶模态振型,如图4所示。张相闻研究试验与仿真的一阶固有频率分别为90.63 Hz，88.4 Hz，本文有限元模型一阶固有频率为88.2 Hz。结果可见，在材料参数，载荷参数和边界条件设置一致的情况下。本文计算结果与张相闻结果较吻合，证明了该有限元建模的有效性。

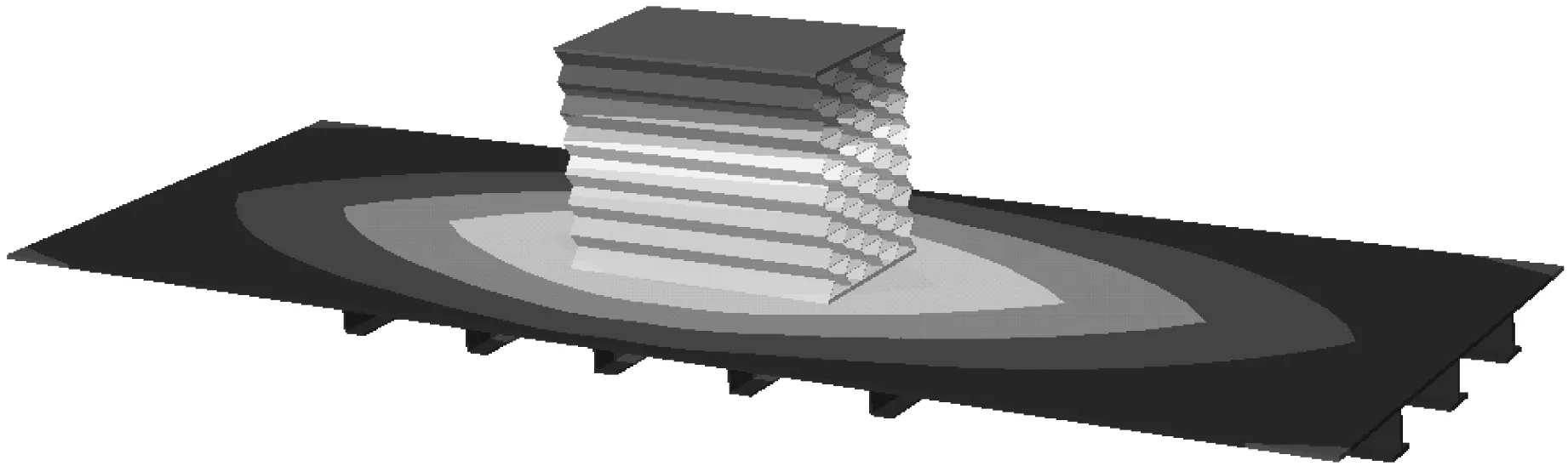
(a) 本文

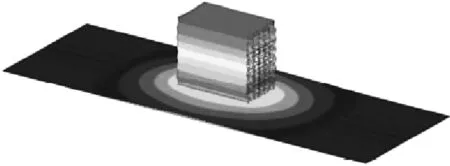
(b) 文献[18]图4 蜂窝隔振基座一阶垂向模态Fig.4 First vertical mode of honeycomb vibration isolation base

在对常规方形蜂窝基座研究的基础上，本文将采用相同的方法建立圆筒状蜂窝基座有限元模型，用于后续讨论它们的刚度及隔振性能。

1.3 筒状蜂窝基座比刚度优势分析

本文为了验证圆筒状蜂窝基座承载性能优异，建立方形蜂窝基座模型和圆筒状蜂窝基座模型，进行了静力对比分析。两种基座模型保持内部蜂窝芯胞元壁厚，胞元内凹角等参数全部一致。

船用隔振基座，不仅要求高强度、高刚度，且需要以轻质为目标。所以工程中一般引用“比刚度”的概念来比较承载能力的好坏。对于轻质蜂窝结构材料，一般对比其比刚度的大小，即相同质量(密度)条件下的承载刚度比较。定义结构抗变形能力的比刚度计算公式如下[19]

k=EI/λ

(1)

式中:k为比刚度;EI为等效刚度;EI=F/S;F为蜂窝结构的作用载荷;S为该作用载荷下产生的位移；λ为线密度，λ=M/h;M为蜂窝基座质量;h为蜂窝材料面内结构长度。

利用有限元软件ABAQUS分别对方形和圆筒状蜂窝基座进行静力学分析。将基座底部施加固定约束，并在基座上顶面施加均布力3 000 N，基座材料均为高强结构钢，胞壁之间选择通用接触且无摩擦。得到基座结构位移云图如图5、图6所示，垂向最大位移均发生在基座上表面，方形蜂窝基座最大位移为3.79 μm，圆筒状蜂窝基座最大位移为11.2 μm。

图5 方形蜂窝基座静载位移云图Fig.5 Static displacement cloud image of square honeycomb base

图6 圆筒状蜂窝基座静载位移云图Fig.6 Static displacement cloud image of cylindrical honeycomb base

通过式(1)计算出方形蜂窝基座与圆筒状蜂窝基座比刚度如表1所示。由表1可知，蜂窝芯胞元参数一致，周期排列组合成不同的基座结构形式其比刚度也不一样。圆筒状蜂窝基座由于其圆筒形的构造，可以让整个基座稳定性更好，当圆筒基座受力时各蜂窝芯能够快速传递内力，内力沿着整个圆周表面扩散和分布，能把所承受的外力变成压力均匀地扩散到圆筒各处，所以整体可以承受较大的压力且受力均匀，避免了传统基座的应力集中现象。蜂窝芯不易破损，与方形蜂窝基座比较，其比刚度提升了12%。因此，本文提出的圆筒状蜂窝基座在承载能力方面具有一定优势。

表1 方形基座与圆筒状基座比刚度分析Tab.1 Analysis of specific stiffness of square base and cylindrical base

1.4 圆筒状蜂窝基座隔振性能评价指标

为了定量分析船舶基座隔振性能，需要在基座面板以及板架上选取相关的评价点。板架取点情况如图7所示，为避免局部共振影响其评价点响应情况，板架取点选择在骨材上，共6个点。基座取点为上顶面螺栓连接点附近共4个点，如图8所示。

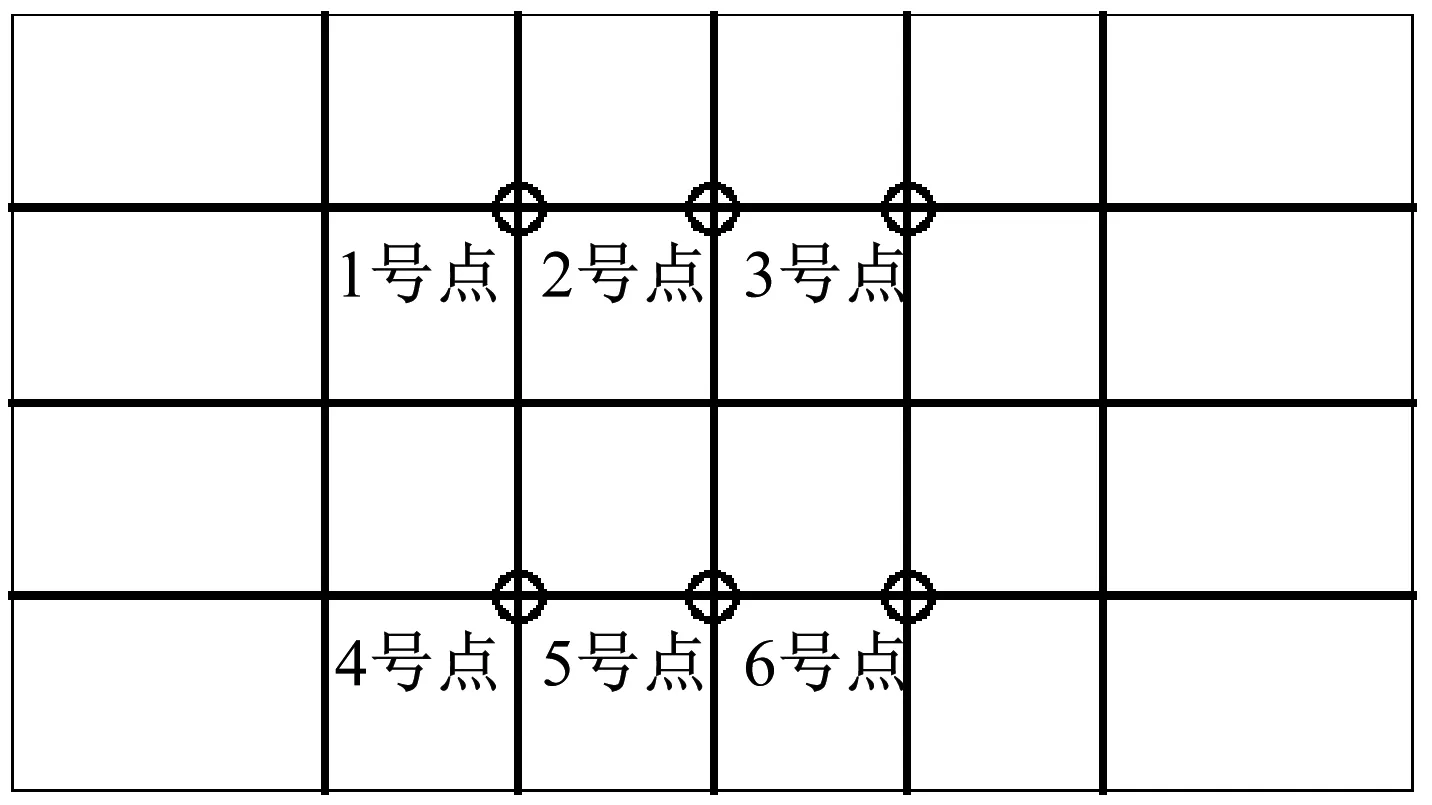
图7 板架评价点分布Fig.7 Distribution of evaluation points of the plate

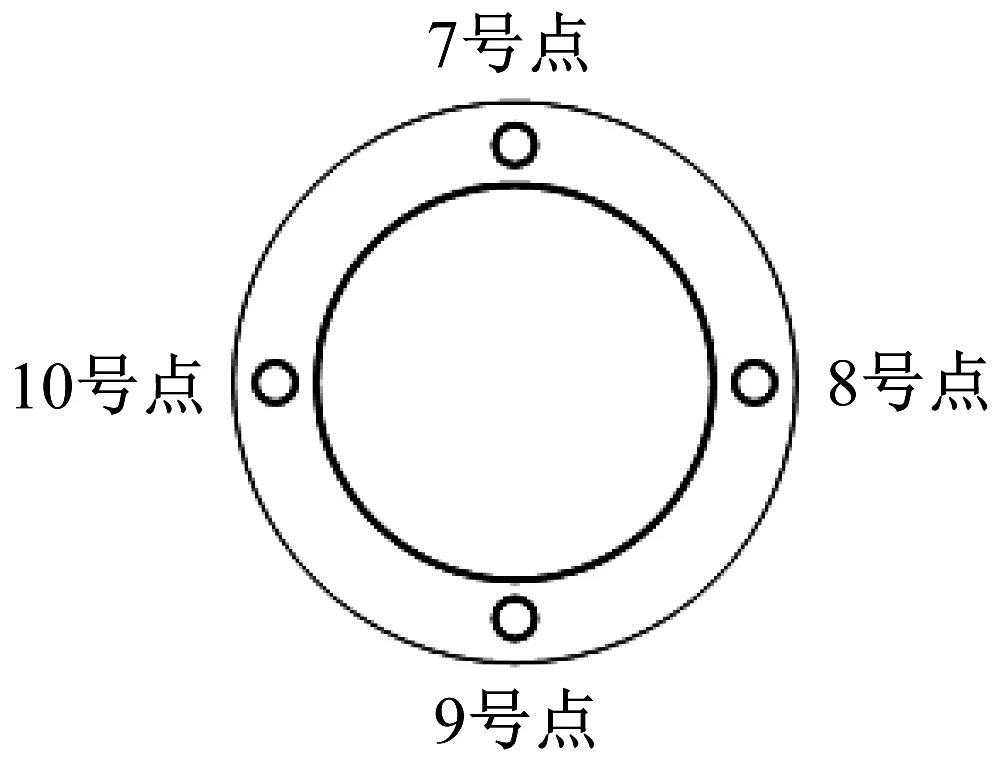
图8 基座上顶面评价点分布Fig.8 Top surface evaluation point distribution on the base

在实际工程应用中，加速度振级落差便于测量、方便计算，可以作为定量评价船舶基座的减振效果。某个频率点下加速度振级表示为

(2)

式中：Li为第i频率点下加速度振级，单位为dB;ar为所取评价点实际加速度响应有效值，单位为mm/s2;a0是基准加速度，根据我国GB 50894—2013《机械工业环境保护设计规范》取10-3mm/s2。

通过式(2)分别计算出基座上面板和板架上各个评价点的加速度振级大小，然后分别对基座上面板4个测点，板架6个测点取平均。由式(3)将各评价点各频率点加速度振级转化为分析频带内平均加速度振级。

(3)

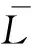
最后取基座上面板测点平均加速度振级与板架测点平均加速度振级的差值，得到振级落差Lr。

(4)

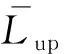
2 基座胞元的隔振性能优化设计

蜂窝基座隔振性能受到胞元参数的影响，由其胞元尺寸定义可知，影响因素有胞元宽度B,胞元高度H，胞元壁厚t，内凹角度θ，为探讨基座隔振性能最佳对应的胞元参数，采用OptiStruct软件对蜂窝基座隔振性能进行优化设计。

优化设计流程首先进行的是动力学响应分析。考虑评价点受激响应情况，用Lanczos法进行频响分析。对其设备质心(质量点)处施加10～1 000 Hz幅值1 000 N的垂向简谐激振力，阻尼系数为2%。计算上文定义的相关测点的加速度响应情况。本文后续所有涉及频响分析的仿真计算均采用相同设置。得到的测点频响曲线如图9所示，基座上顶面7、8、9、10号测点响应情况一致。

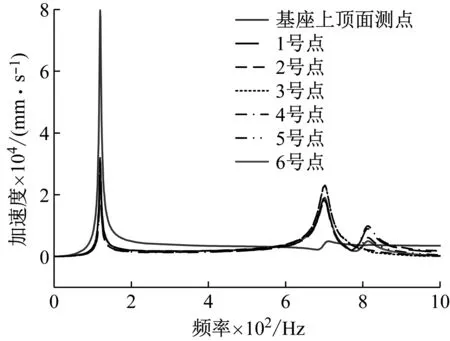
图9 评价点加速度频响曲线Fig.9 Evaluate the point acceleration frequency response curve

由于本文研究的重点在于角度梯度、厚度梯度变化对隔振性能的影响，且为了简化数学列式的求解，所以固定胞元宽度B和胞元高度H构建优化设计。将设计变量定义为胞元壁厚t和胞元内凹角度θ，约束条件为振级落差和屈服应力，目标函数为最小基座质量。

考虑基座屈服应力约束上限和振级落差约束下限，设定振级落差约束下限Lmin，极限屈服应力约束上限σmax，保护结构不损坏。胞元壁厚上、下限分别为tmax和tmin，胞元内凹角上、下限分别为θmax和θmin，根据设计变量、约束条件和目标函数三要素列出优化设计数学列式如下

(5)

式中:胞元内凹角θ取值范围为[-45°，0°];胞元壁厚取值范围为[0.6 mm，4.0 mm];振级落差约束下限为3 dB，最大屈服应力上限为400 MPa，胞元壁厚和胞元内凹角随迭代步变化曲线如图10、图11所示。随着迭代步的不断寻优，胞元壁厚曲线呈下降趋势，壁厚逐渐降低。内凹角度迭代曲线也呈下降趋势，内凹角逐渐增大，最后趋于一稳定值。目标函数迭代曲线如图12所示，总质量降低，符合其轻量化设计目标。振级落差迭代曲线如图13所示，随迭代步增加振级落差增大。从迭代曲线也可以看出，随着胞元壁厚的减小，基座刚度降低，振级落差增大。当胞元壁厚t=2 mm，胞元内凹角θ=0°时，振级落差为1.3 dB;当胞元壁厚取优化下限值t=0.6 mm，胞元内凹角θ=-30°时，振级落差达到最大值为5.01 dB，且基座质量下降了2.6 kg。对比文献[20],胞元结构与本文一致，均为内凹六边形，基座结构不一致，其优化得到的最大振级落差对应壁厚为1 mm，迭代曲线逼近于设计变量最下限，与本文优化得到的结果保持一致，最优壁厚稳定于约束最下限。

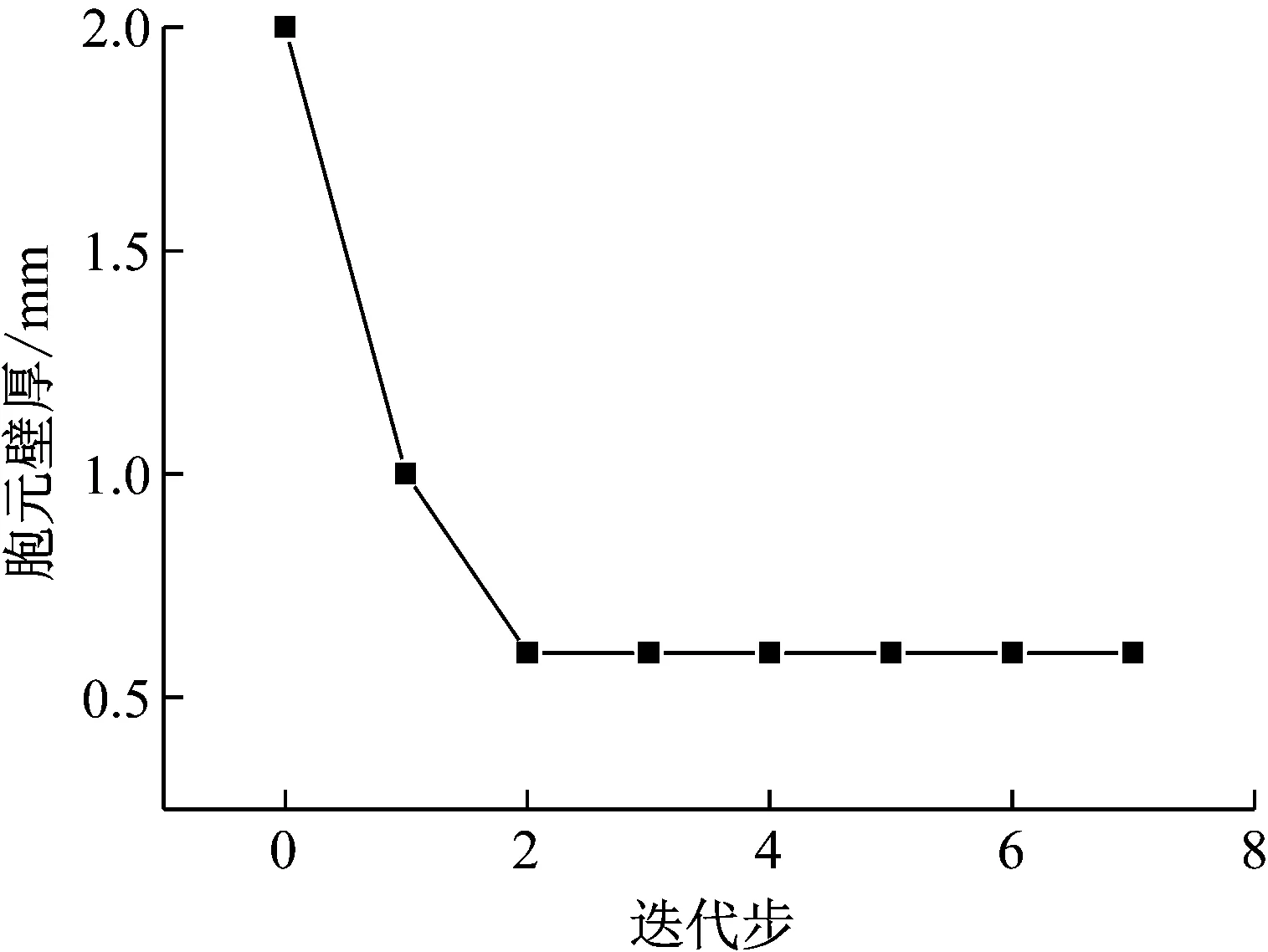
图10 胞元壁厚迭代曲线Fig.10 Cell wall thickness iteration curve

图11 胞元内凹角迭代曲线Fig.11 Cell cell concave angle iteration curve

图12 基座总质量迭代曲线Fig.12 Base total mass iteration curve

图13 振级落差迭代曲线Fig.13 Vibration stage drop iteration curve

3 分层梯度设计对基座隔振性能的影响

在20世纪80年代，“功能梯度材料”的概念首次被日本学者提出。具体指在均匀材料属性中引入不同成分或者在均匀空间构型中引入参数梯度变化，以期实现材料性能呈现梯度变化来控制局部变形模式。本文基于功能梯度材料的概念，以胞元壁厚和胞元内凹角度为自变量，分别设计探讨蜂窝基座隔振性能与厚度梯度、角度梯度变化之间的具体联系。为蜂窝基座隔振性能多目标优化设计提供了可能。

3.1 厚度梯度设计对隔振性能的影响

基于第2章约束振级落差和屈服极限应力优化得到的均匀参数结果，以胞元壁厚为自变量，保持胞元内凹角度一致(30°)。为方便描述，圆筒状蜂窝基座梯度设计没有全部显示，如图14所示，仅展示平面展开的部分梯度分布形式。将该基座沿振源激励方向分成了三层，每一层有两行纵向蜂窝芯胞元，每一层的壁厚保持一致。相邻部分区域的厚度变化量为Δt=±0.4 mm， 从基座上顶面至基座下底面，定义Δt>0为顺厚度梯度，即沿着振源激励方向，蜂窝基座相对密度逐渐增大。反之逆厚度梯度，沿振源激励方向，蜂窝基座相对密度减小。

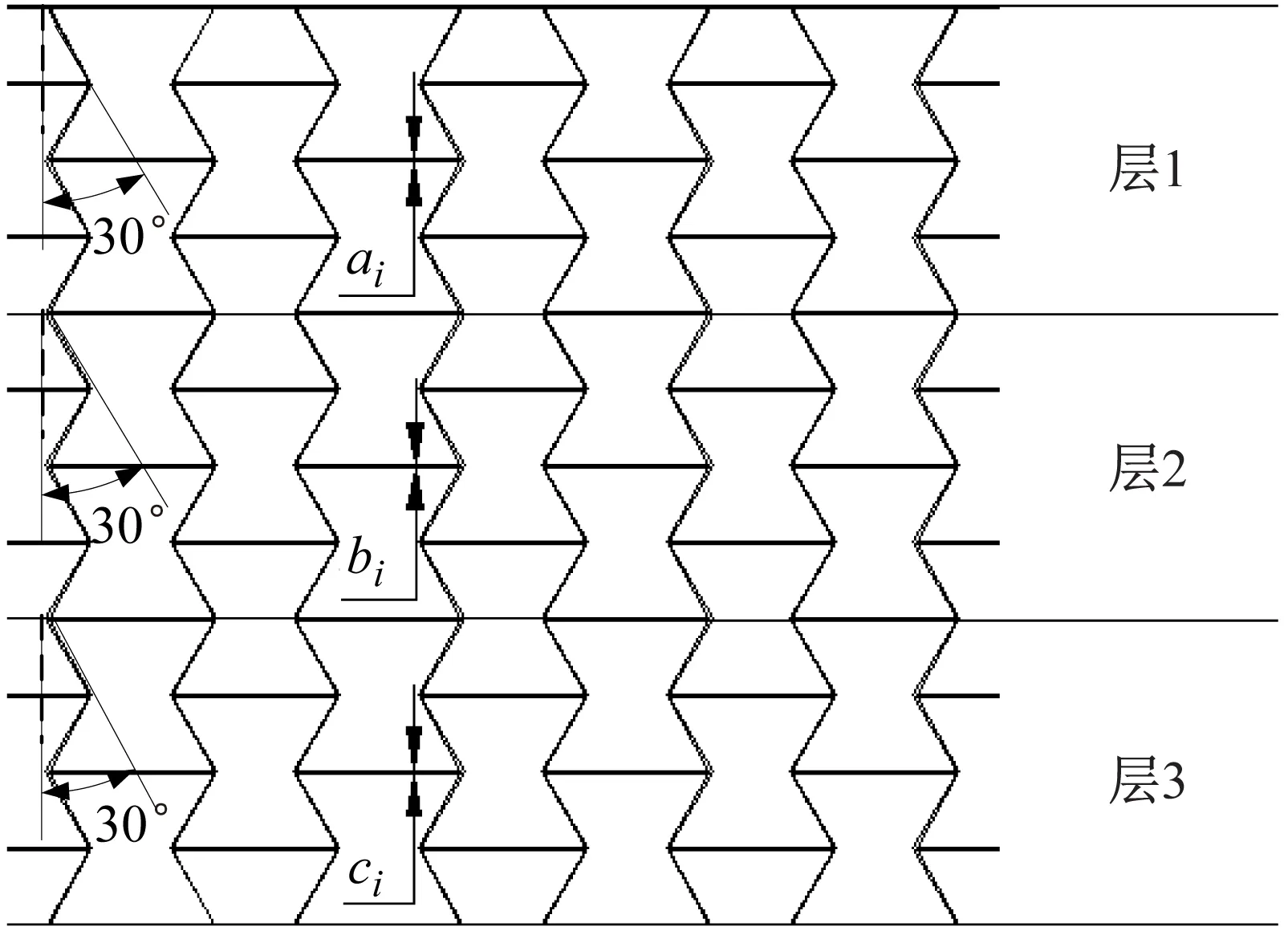
图14 厚度梯度型蜂窝基座结构示意Fig.14 Thickness gradient honeycomb base structure schematic

为了研究质量体积不变前提下，蜂窝基座厚度梯度设计对隔振性能的影响，本节设置同一胞元内凹角下顺厚度梯度、逆厚度梯度两种工况进行频响分析。具体梯度参数设计如表2所示。

表2 厚度梯度参数设计Tab.2 Thickness gradient parameter design

由于均匀厚度基座在第2章已经计算，本节仅对顺厚度梯度与逆厚度梯度基座进行频响分析，得到基座上面板测点平均加速度振级与板架测定平均加速度振级曲线如图15、图16所示。由图15、图16可知，两种梯度基座频响曲线变化几乎一致，基座一阶垂向振动固有频率为110 Hz左右，基座上面板测点平均加速度与板架测点平均加速度差值有微小差异。

图15 顺厚度梯度基座上面板和板架平均加速度振级对比Fig.15 Comparison of mean acceleration vibration level between panel and frame on base along thickness gradient

图16 逆厚度梯度基座上面板和板架平均加速度振级对比Fig.16 Comparison of mean acceleration vibration level between panel and frame on inverse thickness gradient base

3.2 角度梯度设计对隔振性能的影响

本节主要探讨角度梯度变化对基座隔振性能的影响，所以控制基座厚度不变，其他分层设置与3.1节保持一致，如图17所示，每两层胞元一个角度，相邻部分内凹角度变化量Δθ=5°。从基座上顶面至基座下底面，定义胞元内凹角逐渐变大为顺角度梯度，即沿振源激励方向，相对密度逐渐增大，反之为逆角度梯度，沿振源激励方向，相对密度逐渐减小。具体梯度参数设计如表3所示。

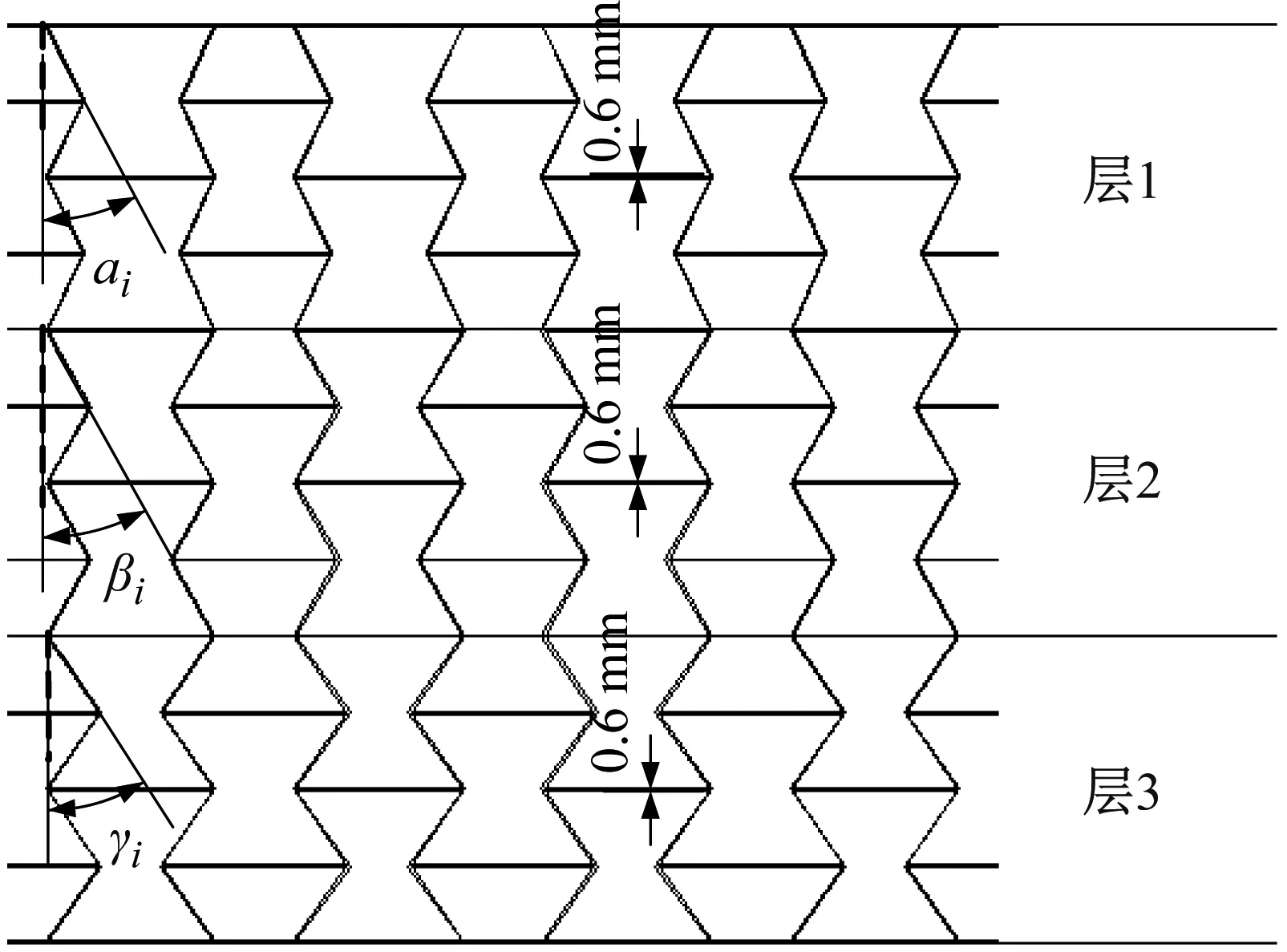
图17 角度梯度型蜂窝基座结构示意Fig.17 Structure diagram of angular gradient honeycomb base

表3 角度梯度参数设计Tab.3 Angular gradient parameter design

均匀胞元壁厚、均匀胞元内凹角频响分析已计算，本节对顺角度梯度、逆角度梯度基座分别进行频响分析。基座上面板测点平均加速度振级与板架测点平均加速度振级曲线如图18、图19所示。基座一阶垂向振动固有频率为119 Hz左右。角度梯度的变化并没有较大影响加速度响应曲线。

图18 顺角度梯度基座上面板和板架平均加速度振级对比Fig.18 Comparison of mean acceleration vibration levels of panel and frame on base along angular gradient

图19 逆角度梯度基座上面板和板架平均加速度振级对比Fig.19 Comparison of average acceleration vibration level between panel and frame on inverse angular gradient base

3.3 结果与讨论

由式(3)、式(4)计算上述仿真结果，得到各梯度基座振级落差如表4所示。由几种基座隔振性能对比可看出，厚度梯度的设计有利于提升基座隔振性能，逆厚度梯度基座隔振性能最好，逆厚度梯度基座较之均匀参数基座隔振性能提升了21%，顺厚度梯度基座对隔振性能的提升略低于逆厚度梯度基座；角度梯度的设计对基座隔振性能影响不大。

表4 振级落差结果对比表Tab.4 Comparison table of vibration stage drop results

综合加速度振级曲线以及基座振级落差结果可以得出：分层梯度设计不影响加速度振级曲线变化趋势，对于厚度梯度型蜂窝基座，应采用逆厚度梯度基座，即机械设备安装于胞元壁厚较大的蜂窝层隔振效果最佳，随着胞元壁厚的分层减小，加速了衰减过程，隔振效果显著。

4 结 论

本文提出了一种圆筒状蜂窝基座，分析了圆筒状蜂窝基座的抗变形能力，对该蜂窝基座进行隔振性能参数优化设计，基于优化得到的匀质设计参数，以胞元壁厚和胞元内凹角为自变量，分别讨论了厚度梯度设计、角度梯度设计对基座隔振性能的影响，结论如下：

(1) 蜂窝基座隔振性能的提升可以通过优化设计结合分层厚度梯度设计来实现，胞元壁厚越薄其基座刚度越低，振级落差越大，隔振效果越佳。

(2) 厚度梯度基座较之均匀参数基座隔振性能有所提升，逆厚度梯度基座隔振效果最佳，隔振性能提升了21%，角度梯度的设计对隔振性能影响不大，建议工程实际中采用逆厚度梯度等内凹角蜂窝芯胞元设计。

(3) 圆筒状的设计能增加基座比刚度，整体能承受较大压力且受力均匀，避免了应力集中，较之于规则方形基座，比刚度提升了12%，承载能力更强。该圆筒状基座构思可方便地推广到诸多设备基座设计中。