挠性印制板基板自然对流换热仿真研究

寻千秋 王志宝

（苏州维信电子有限公司，江苏 苏州 215100）

0 引言

随着电子行业的发展，印制电路板（printed circuit board，PCB）正向小型精密化和高频高速化方向发展，这对PCB 的热可靠性提出了更大挑战。在电子产品设计中，热仿真分析能够有效改善电子产品性能，提升产品可靠性，提高产品市场竞争力［1］。近年来，国内外许多学者针对PCB设计提出了许多热分析技术。

在理论研究方面，Janicki等［2］运用格林函数求解多热源的多层PCB 传热方程，并获得PCB 温度分布。Zhang 等［3］提出了一种基于傅里叶级数变换和笛卡尔网格的有限体积分析法，研究PCB线路和热过孔对PCB 传热能力的影响。陈文虎等［4］建立了求解PCB空芯冷板散热的强迫对流数学理论模型，并验证了此模型求解的正确性。汪玲等［5］对比研究了三维模型导入法与常用的覆铜层等效导热系数仿真法，结果表明三维模型导入法优于等效导热系数仿真法。

在应用研究方面，李长民等［6］总结了某PCB布线中电流生热仿真法，通过理论计算与Flotherm 计算结合的方法得到模型的温度分布。马岩［7］利用Icepak研究某PCB结构及元器件板级热设计，分析PCB 在热传导与强迫对流换热下的温度分布。契程亮［8］利用Flotherm 研究了PCB 铜厚、直流变换器（DC converter，DCDC）效率、散热片、外壳等因素对PCB散热的影响。黄艳飞［9］利用Icepak 软件结合模拟退火算法优化PCB 板上电子器件的布局，降低了电子设备的最高工作温度。李逵等［10］通过热仿真分析和实验测试研究石墨复合PCB 板、普通PCB 板和铝基板的散热性能，验证了石墨复合PCB板的优异热传导能力。

综上所述，众多学者针对PCB 热分析及散热改善展开多方面的深入研究，涵盖理论分析、实践应用等方面。大部分研究是针对PCB 元器件为热源展开，忽略了PCB 内部线路本身产生的焦耳热及其影响。对于PCB 中的挠性印制电路板（flexible printed circuit board，FPCB），目前自然对流下的热分析研究极少，相关经验系数并不完全适用于FPCB，因此开展FPCB 的热仿真分析技术显得尤为重要。基于此，本文针对某规格的FPCB 基板—挠性覆铜板（flexible copper clad laminate，FCCL）做机理性方面的热电流耦合仿真分析，同时考虑了铜线宽度以及电流大小对FPCB 在自然对流下换热的影响，分析结果可为FPCB产品端热分析提供参考依据。

1 物理模型及网格划分

为了研究FPCB 自然对流换热的规律，需要对物理场准确建模。本文分别以单层和双层FCCL为研究对象，基材长度均为450 mm，单面基材铜层厚度为12.0 μm，聚酰亚胺（polyimide，PI）层厚度为12.0 μm，双面基材铜层厚度13.5 μm，聚酰亚胺层厚度为12.0 μm，周围建立尺寸为400 mm×420 mm×450 mm的空气域，如图1所示。

图1 FPCB仿真计算模型

采用结构化网格对物理模型划分三维网格。为了保证壁面Y+接近1，第1 层网格高度设为1×10−5mm。由于FCCL 厚度为微米级，为了保证网格长宽比，分别在宽度和长度方向加密，最终网格数量为250万，如图2所示。

图2 FPCB仿真网格示意

2 数学模型

2.1 自然对流换热数学模型及边界条件

对于FPCB的应用场景，由于板面少有功率元器件，其热流密度相对较低，大部分情况下无需采用强迫对流散热，在自然对流状况下完成换热。

连续性方程如下：

式中：u、v、w分别为3个方向上的速度分量，m/s；x、y和z分别为3个方向上的尺寸分量，m。

动量方程如下：

式中：ρ为空气密度，kg/m³，作重力项时为温度的函数；μ为分子动力黏度，Pa·s；p为压力，Pa；T为介质温度，℃；T0为周围环境空气的参考温度，℃，取26 ℃；gz为z轴方向的重力加速度分量，m2/s；β为参考温度下的空气热膨胀系数，取值为0.003 67；

能量方程如下：

式中：λ为介质导热率，W/（m·K）；Cp为介质的比热容，J/（kg·K）；S为源项，流体域的能量方程不包含源项，即S=0，且Cp为比定压热容；固体域能量方程中u=0，v=0，w=0，S即为焦耳热源项，且σ为固体介质电导率，S/m；φ为电势，V。

设定边界条件为空气域外侧，给定压力出口边界条件，压力值为101 325 Pa，将FCCL 在空气域内部的表面定义为无滑移壁面，指定其端面的电流密度，开启焦耳热计算模型，各壁面热边界条件均为耦合边界条件，环境温度26 ℃。

自然对流分为层流自然对流和湍流自然对流，判断依据一般为瑞利数，可得方程式如下：

式中：Ra为瑞利数；g为重力加速度，取值9.81 m2/s；L为特征长度，m；△T为温差，℃；α为热扩散系数，m2/s，取值0.000 024 m2/s。

一般，Ra大于1×108时，散热过程为湍流自然对流，本文Ra为3.7×107，因此采用层流模型、Coupled耦合算法进行求解计算；压力离散格式采用体积力加权，动量与能量离散格式采用Ⅱ阶迎风格式。

2.2 材料

本文的FCCL 材料为铜和聚酰亚胺，其主要物性参数见表1。铜的电导率是温度的函数，随着温度升高而变化，如图3所示。本研究已将温度对铜的电导率影响拟合到计算软件中。

表1 FPCB仿真材料属性

图3 铜的电导率随温度变化曲线

3 计算结果分析

3.1 实测数据比对

为了验证仿真数据的准确性，实测FCCL 铜层表面最高温度，并与仿真数据对比。采用直流稳压源分别对单面板和双面板通入直流电，调节稳压源电压，实现FCCL 的不同电流加载，使用手持红外热成像仪采集温度数据，各仪器如图4所示。

图4 FPCB实测仪器示样

单面板不同电流和双面板不同线宽条件下，FCCL铜层表面最高温度的测试结果与仿真结果比对如图5所示。由图可知，仿真结果与实测结果吻合较好，误差为0.5%～4.0%，最大误差出现在单面板10 A时，在工程应用领域可被接受。

图5 仿真数据与实测数据对比

在FPCB 实际线路设计中，主要参数为加载电流I和铜线宽W。本文针对这2 个参数展开研究，加载电流I分别取1、5、10 和15 A，铜线宽W分别取15、20和30 mm。

3.2 单面板电流的影响

当W=20 mm 时，不同截面的电流流速云图如图6所示。由图可知，FCCL 表面空气对流效果明显，不同电流加载下的流场具有共同现象，即在FCCL热源加热后空气发生膨胀，密度减小。在浮力作用下，气流在FCCL 中间表面位置呈旋流汇聚，并向上运动，在顶部出口位置向两侧分散运动，整体上呈对称分布。在低电流，即低Ra数时，FCCL表面流速明显低于高电流，尤其是正中间的低流速区域的范围随着电流增加逐渐减小，对流现象更加明显。这是因为电流增加时，FCCL表面温度随之上升，与周围环境空气的温差变大，FCCL 表面气流密度差也随之增大，浮力作用增强，自然对流的幅度也随之加大，导致FCCL 表面气流流速加快。

图6 W=20 mm，不同电流流速分布云图

与流场一样，温度场围绕中心线呈对称分布，如图7所示。不同电流下，X=0平面高温区在FCCL上方呈锥型向外扩散，随着电流增加，锥形区域面积逐渐增大，对流换热作用增强，靠近FCCL处的温度梯度较大，电流为1 A时，Ra数相对较低。由图7可知，在4种电流加载下，此种情况对流作用较弱，温度梯度较小。FCCL与空气的导热在整个换热过程中十分重要，Ra数随着电流增加而增加，对流效果更加明显，且以对流换热为主。

图7 W=20 mm，不同电流温度分布云图

3.3 线宽的影响（单面板）

不同线宽下，流场整体分布与上述分析一致，如图8所示。随着线宽增加，FCCL 横截面面积增大，阻值减小，同等电流下焦耳热随之减小，自然对流换热作用相对减弱。FCCL表面的高速区范围随着线宽的增加而减小，表明在一定电流加载的情况下，适当加宽铜线有助于减少FCCL 产生热量，同时FCCL 的表面积随着线宽的增加而增大，有利于增强自然对流换热。

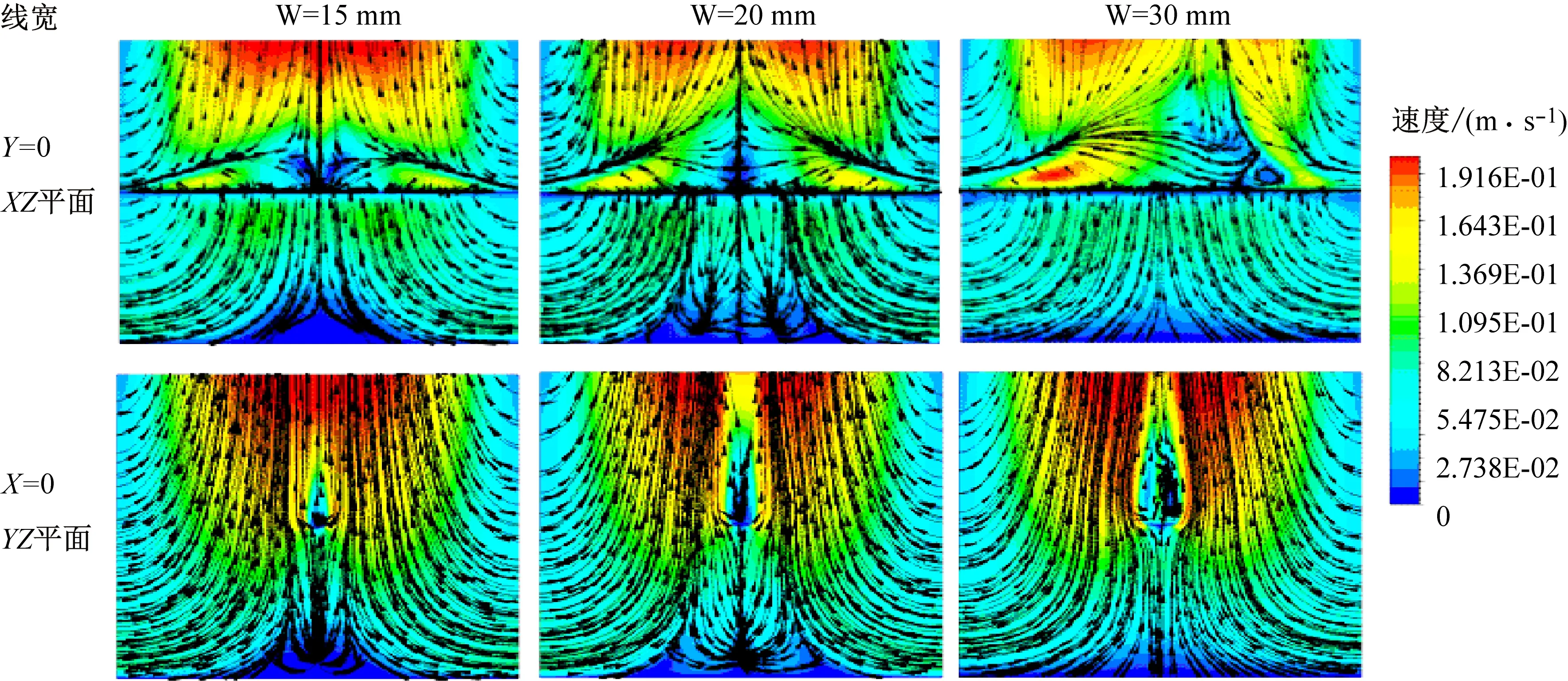
图8 I=5 A，不同线宽流速分布云图

不同线宽下的温度场分布如图9所示。温度场围绕中心线呈对称分布，X=0 平面的高温区在FCCL上方呈锥型向外扩散，随着线宽增加，锥形区域面积逐渐缩小，温度梯度和数值逐渐减小。一方面是因为FCCL 产生的焦耳热量减少，另一方面FCCL表面积增加有利于散热。

图9 I=5 A，不同线宽温度分布云图

3.4 换热特性比对（单面板与双面板）

为了给实际工程应用提供指导，需要提取对流换热系数，对FCCL 上、下壁面的平均换热系数h展开分析，可得方程式如下：

式中：Tw为固体壁温，℃；A为导热垂直方向截面积，m2。

不同电流与线宽情况下，铜层与聚酰亚胺（PI）层表面平均换热系数比对如图10和图11所示，换热系数的数值范围为4.2～12.5 W/（m2·K）。由图可知，FCCL上表面的换热效率与下表面相比显著降低，其下表面与低温流动空气完全接触，换热效率高，由于FCCL 的阻挡，空气在向上流动的过程中被加热，同时在宽度方向两侧的流动相对较快，而上表面中间区域气流流速较慢，因此FCCL 上表面换热效率较低。同时单面板与双面板表面的平均换热系数分别随电流的增加而增大，随着线宽的增加而减小。

图10 单面板换热系数h比对

图11 双面板换热系数h比对

由图10可知，电流由1 A增加至15 A时，单面板铜层表面h由5.85 W/（m2·K）变为7.52 W/（m2·K），提高28.5%；PI 层h由9.95 W/（m2·K）变为11.7 W/（m2·K），提高17.5%，增长幅值小于铜层表面，说明电流增加时，上表面的换热效果提升更加明显。电流由10 A 增加到15 A 时，单面板铜层表面换热效果的提升趋于平缓；双面板上层铜表面h由4.65 W/（m2·K）变为6.8 W/（m2·K），提高46%；下层铜表面h由9.9 W/（m2·K）变为10.9 W/（m2·K），提高10%。

综上所述，随着电流的增加，双面板上下铜表面的平均换热系数变化规律与单面板不同，电流为10～15 A 时，两者上升趋势更明显，这是因为双面板的两层铜均为热源，电流增加时，双热源焦耳热的增加多于单热源焦耳热。

铜线宽由15 mm 增加至30 mm 时，单面板铜层表面h由7.2 W/（m2·K）变为5.7 W/（m2·K），减小20.0%；PI 层表面h由11.5 W/（m2·K）变为8.4 W/（m2·K），减小26.9%。双面板上层铜表面h由6.3 W/（m2·K）变为5.7 W/（m2·K），减小9.5%；下层铜表面h由11.8 W/（m2·K）变为9.3 W/（m2·K），减小21.2%。由图11可知，电流一定时增加线宽，单面板与双面板上下表面的平均换热系数减小趋势保持一致。

4 结语

（1）本文对于FPCB 基板FCCL 的对流换热仿真结果是可信的，不同电流I和不同线宽W的温度数据与实测结果对比较好，对比误差为0.5%～4.0%，可采用该仿真方法分析FPCB 散热问题，对于工程设计具有指导意义。

（2）随着加载电流的增加，FCCL 发热量增加，表面温度逐渐升高，对流换热幅值增加，空气流场中对称分布结构也随之发生变化，热气流逐渐靠拢上浮。电流由1 A 增加至15 A 时，单面板铜层表面平均换热系数提高28.5%，PI 层表面换热系数提高17.5%；双面板上层铜表面平均换热系数提高46%，下层铜表面平均换热系数提高10%。电流增加至15 A 时，单面板的h增加趋势逐渐平缓，双面板趋于线性变化。

（3）随着铜线宽的增加，FCCL 发热量减少，表面温度逐渐降低，对流换热幅值减小。线宽由15 mm 增加至30 mm 时，单面板铜层表面h减小20.0%，PI层表面h减小26.9%；双面板上层铜表面平均换热系数减小9.5%，下层铜表面平均换热系数减小21.2%，两者变化趋势基本一致，均趋于平缓。