智慧馆员视角下线性回归分析课堂教学探索
胡 乙
(江苏经贸职业技术学院,江苏 南京 211168)
引言
针对智慧馆员数据分析课程教学研究,目前国内外尚未有专门论述。罗格尔[1]从培养数据科学家角度,主张以python为工具,系统地介绍当今数据科学与数据分析中使用的通用算法及背后的数学思想。针对初学者,周红[2]主张利用电子表格Excel强大的函数功能学习线性回归、聚类、交叉验证等数据挖掘方法。国内研究中,吕盛坪[3]、王海林、李君讨论了现有数据分析与挖掘软件的不足,提出重新开发个性化的学习平台以适应数据分析教学需要。但目前多数数据分析软件或者平台对学生隐藏了数学模型的构建步骤,省略了几乎所有公式的建立与推导过程,故学生难以理解数据挖掘与分析背后隐藏的数学原理。区别于流行的工具,Excel可以让学生以一种完全透明的方式处理数据。对于初学者而言,Excel是物美价廉且功能强大的数据分析学习工具,值得学生实践。据此,研究拟从数理统计理论与数据分析软件实践两方面出发,引导学生理解回归分析、回归模型、回归方程、估计的回归方程、判定系数等相关概念。同时,以Excel为工具建立样本数据库,引导学生分步骤建立所有相关公式,使学生深入了解回归分析的数学原理与软件操作方法,为后续学习更高级的数据挖掘与分析课程打下理论与实践基础。
一、智慧图书馆、智慧馆员与大数据分析
智慧图书馆的特征就是收集、形成大数据,并利用算法进行数据挖掘与分析,以提供智慧与知识服务。
(一)智慧图书馆与大数据分析
伴随物联网、云计算、大数据分析等信息技术的不断进步,特别是阿尔法机器人在围棋比赛中的出色表现,智慧图书馆与人工智能技术日益受到学界重视。智慧图书馆一词,最早于2003年由芬兰奥卢大学图书馆Aittola等人提出,智慧图书馆是不受空间限制的,可被感知的移动图书馆[4]。大数据是海量庞杂的数据,其特征包括数据大量化、类型多样化、处理快速化、分析复杂化等。智慧图书馆的智慧来源就是大数据,图书馆的大数据分为生产大数据与分析大数据两方面。此外,图书馆保留了科研与生产数据,且科研数据管理与服务也成为智慧图书馆服务的新热点。科研数据管理涵盖了数据管理标准制定、元数据创建、语义注释、数据关联等活动。而科研数据服务一般包括创造和管理机构数据、提供数据挖掘与可视化工具等,要实现以上目标,开展智慧馆员数据分析教学研究刻不容缓。
(二)智慧馆员与数据科学课程
“没有智慧馆员,就没有智慧图书馆”[5]。伊安·约翰逊深刻指出了智慧馆员对于智慧图书馆建设的重要性。由于目前国内外尚缺乏统一定义,研究将智慧馆员定义为在新兴技术背景下,以满足用户个性化需求为目的,能提供数据管理服务、智慧智能服务的新型图书馆学情报学人才。其能在数据管理基础上,为科研人员提供数据开发、数据搜集、数据分析等科学数据服务。据此,智慧馆员型图情专业学生应学习数据科学与分析课程,掌握数据分析概念、数据性质、数据分析过程。其中,回归分析是解决变量间关系难题的最基本的数据分析方法,深刻理解回归分析背后的数学原理与实践过程,有助于学生学习数据分析与挖掘高级技术,成为更好地知识服务提供者与指导者。
(三)回归分析的数学原理与相关概念
数据分析中最常见的是对两个变量之间关系的分析。例如,管理人员可运用最高气温与图书馆自习人数的关系,根据未来最高气温的预报值,来估计对应图书馆的自习人数。传统上人们经常依靠个人直觉与经验判断两个变量的关系,但如果能取得样本数据,则可以运用数据分析方法建立方程来描述变量之间相互关系,以上方法即为回归分析。
1.回归模型与回归方程
在回归分析中,被预测的变量y为因变量,而用来预测因变量的一个或者多个变量称为自变量x。其中最简单的回归分析称为简单线性回归,它只包括一个自变量与因变量,可以用一条直线近似描述二者关系。以气温与图书馆自习人数为例,因为图书馆有免费空调和免费书刊等学习资源,故通常气温越高,则图书馆自习人数越多。从回归分析中可以建立气温影响自习人数的方程。区别于单一的样本,从总体考虑,假设总体是由所有特定类型图书馆组成的集合,则对于总体中每一个图书馆都有一个气温值x与自习人数y,描述y依赖x与误差项的方程称为回归模型,其中简单线性回归的回归模型为y=β0+β1x+ε。模型表示:β0与β1为模型的参数,ε为误差项,误差项描述了包含在y中但不能被x与y之间线性关系解释的变异性。图书馆总体也可以视为由若干图书馆子集组成的全集,每一个子集都对应一个y的分布,而y的每一个分布都有自己的平均值或者期望值。据此可引出回归方程概念。回归方程是描述x如何影响y的期望值E(y)的方程,其中,简单线性回归方程为:E(y)=β0+β1x[6]。该方程的图形是一条直线,β0是回归直线的y轴截距,β1是斜率或者导数,
2.估计的回归方程系数与最小二乘法
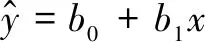
公式1
公式2

3.误差平方和与判定系数

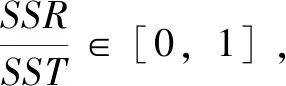
二、电子表格函数的运用与回归分析实践
在课堂教学中,Excel能以一种清晰的方式处理数据,在Excel中有三种方法可构建估计的回归方程,即组合函数、数组函数、趋势线。
(一)电子表格函数与最小二乘法的实践

第二种计算系数的方法是利用电子表格内置的Linest函数,在M1中输入b1,在N1中输入b0,选中M2:N2,输入“=LINEST(C2:C11;B2:B11,TRUE,TRUE)”,按住CTRL+SHIFT+ENTER后显示b1、b0。该函数为数组函数,输出个数为n+1,其中n是自变量个数。该函数先计算斜率,后计算常数。同时,该函数先输入因变量数组,后输入自变量数组,数组公式中出现大括号表示函数是数组函数。

(二)电子表格函数与判定系数的计算
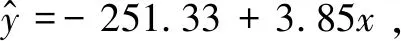
以此类推,可计算SSE=308,SST=3812。在J12中输入“=(H12-G12)/H12”,可得r2=0.919,可见,图书馆自习人数变异性的约92%能被估计的回归方程所解释,拟合程度较高。
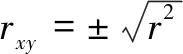
大数据为智慧图书馆发展提供了难得的机遇,分析应用大数据是获得智慧的关键。建设智慧图书馆,提供知识服务,首先要培养合格的智慧馆员。智慧馆员应掌握信息分析、数据挖掘、机器学习、网络安全与维护等技术与知识。智慧馆员在一定程度上可以说是一名优秀的数据科学工作者。当前随着数据量急剧增加,从已知大数据中发现统计规律,进而利用这些规律来计算未来生产、工作中的估计值,已经成为智慧馆员智慧服务的热点之一。深入学习简单线性回归概念及应用、有助于为后续学习打下坚实基础。
结语
在进行回归分析时,对于简单线性回归方程,可利用最小二乘法分别求出方程参数β0、β1的估计值b0、b1,从而得到估计的回归方程。
利用r2能测量估计的回归方程的拟合度,但仅仅根据判定系数值,不能得出变量间关系在统计学上是否显著的结论。这一结论必须建立在对最小二乘法估计量抽样分布性质的研究上。在对假定模型的合理性进行检验前,仍然不能应用这个估计的回归方程,要确定假定的模型是否合理,则要对变量间关系的显著性进行检验。
未来课堂教学研究应引导学生对模型的误差项ε作出概率假设,并对变量间关系的显著性进行统计检验,同时运用Excel创新实践教学研究。

