应变速率对零件加工过程材料性能影响分析
李炎粉,李雪珂,刘义付,杨铁皂
(1.黄河交通学院汽车工程学院,河南 焦作 454950;2.河南科技大学,河南 洛阳 471000)
1 引言
汽车用钢板的加工过程并非绝对的静态过程,而是在较低的速度下的准静态过程。HC340LA是一种常用的汽车结构钢,具有良好的吸能特性,应用广泛[1]。在较低的应变速率下材料的力学性能和加工硬化与静态时特征相比,均发生了一系列的变化;如果仍以静态力学性能进行表征加工过程,则存在较大的误差。因此,对材料在不同应变速率下性能的变化趋势,对成形加工分析和模具设计具有重要的参考意义。
国内外学者对此进行了一定的研究:文献[2]采用网格应变的方式,对加工前后材料变形过程厚度变化进行测试;文献[3]采用在线应变测试技术,对汽车零件加工过程材料性能变化进行测试;文献[4]采用有限单元法,模拟材料的加工过程中应变的变化规律;文献[5]采用试验与模拟相结合的方法,对不同的冲压速度影响材料性能进行分析。
针对材料成形过程中应变速率对性能影响进行分析,选取HC340LA进行8个准静态低应变速率拉伸性能测试,获取不同应变速率下材料的力学性能变化和加工硬化变化,同时基于John⁃son−Cook模型获取材料的应变速率敏感性因数;将应变速率的影响嵌入到有限元仿真分析模型中,获取材料的成形极限FLD图,并与试验结果和经验公式结果进行对比;为指导实际设计生产提供参考依据。
2 试验材料和过程
2.1 试验材料
所研究的HC340LA 组织,如图1所示。由铁素体和珠光体组成[6]。化学成分,如表1所示。
图1 HC340LA组织Fig.1 HC340LA Organization

表1 材料化学成分Tab.1 Chemical Composition
2.2 试验过程
整个实验依据GB/T 30069.2−2016和ISO 26203−2:2011[7−8],试样尺寸,如图2所示。试样编号、拉伸速率及应变速率,如表2所示。

图2 试验用拉伸试样Fig.2 Tensile Test Specimen
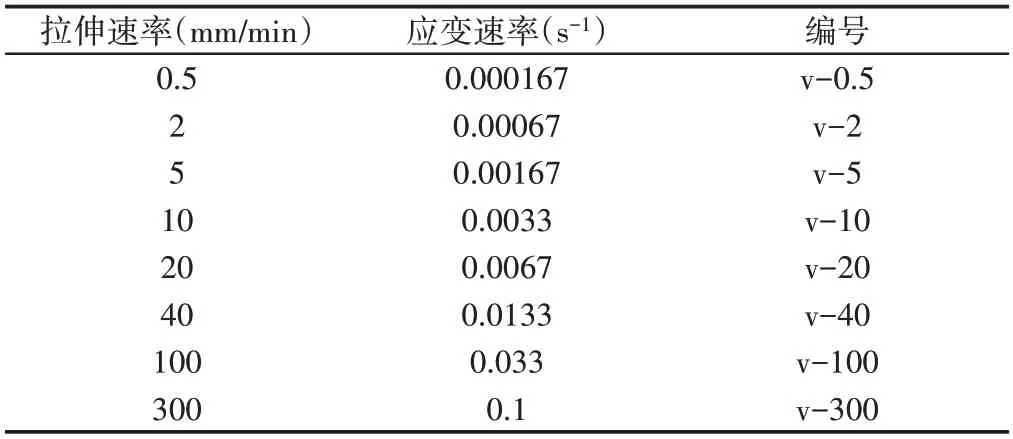
表2 拉伸速率与应变速率对应Tab.2 Tensile Rate Corresponds to Strain Rate
3 对性能影响分析
3.1 力学性能变化
根据试验结果,获取不同的拉伸速率下材料的性能,如表3所示。所得曲线,如图3所示。

表3 不同应变速率下力学性能Tab.3 Mechanical Properties at Different Strain Rate

图3 不同应变速率工程应力应变曲线Fig.3 Stress and Strain Curves of Different Strain Rate Engineering
根据图3所示可以看出,不同的应变速率下HC340LA 在拉伸工程应力应变曲线上都有较短的屈服平台和上下屈服点,得出不同应变速率并不能消除HC340LA 的屈服平台,可见在HC340LA试样拉伸过程中形成了柯氏气团[9],继续拉伸过程中位错摆脱气团的钉扎,出现屈服平台。同时可以发现,材料的断后延伸率随应变速率的增大而减小,而强度则随之而增大。
根据表2和图3力学性能和曲线,获取不同参数随应变速率的变化曲线,如图4所示。
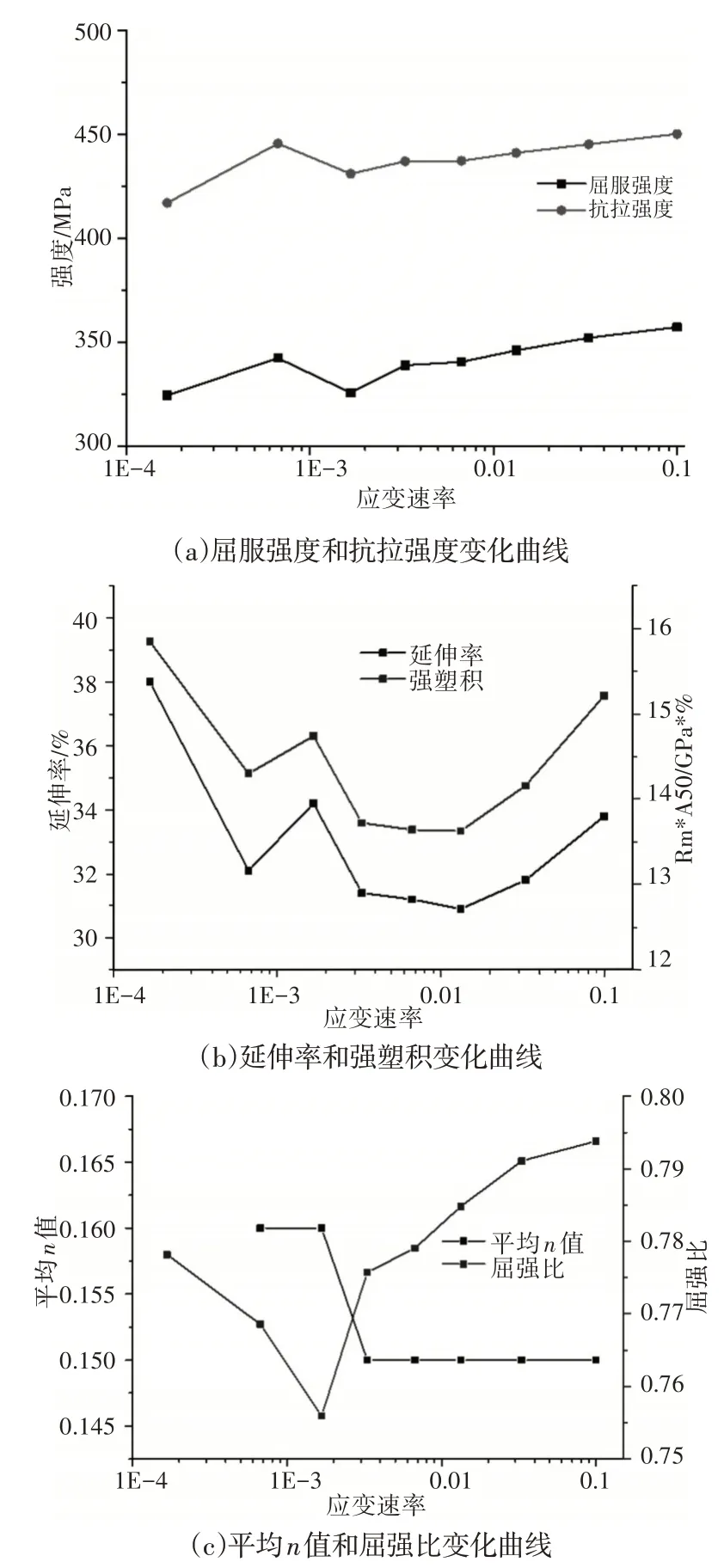
图4 各参数变化曲线Fig.4 Variation Curve of Each Parameter
由图中所示曲线变化可以知道,随着拉伸速率的提升,材料的强度整体呈现出缓慢增加的趋势,抗拉由324.5MPa 增加到357MPa,而抗拉强度则由417MPa增加到450MPa。同时,观察屈服强度和抗拉强度变化曲线,两者的变化规律较一致,根据屈强比的变化曲线也可以得出,屈强比的变化随着应变速率变化幅度很小,因此可以得出,应变速率对HC340LA的屈服强度和抗拉强度的影响规律一致。根据图4(b)中HC340LA不同应变速率拉伸的延伸率和强塑积变化曲线可以看出,延伸率和强塑积都是随着应变速率的增大先较小,最后在应变速率为0.0133/s时又开始随着应变速率的增大而增大,但是延伸率还是在应变速率最低是最高,究其原因是:在低的应变速率下,组织变形协调充分,降低了应力集中现象,不宜出现微缩孔洞导致材料拉伸断裂。同时观察测试得到的平均n值,随着应变速率的变化,基本不变。
3.2 材料应变速率敏感性因数
Johnson−Cook本构模型可以描述材料不同应变速率下的力学特征[10],表达式如下所示:
式中:σ—等效应力(MPa);εp—等效塑性应变;—无量纲塑性应变率;其他4个待定的参数A、B、n、C是与材料相关的系数。试验中选取拉伸速度为最慢0.5mm/min,即拉伸速率为0.000167s−1作为准静态拉伸速率。为按照式(3)计算得出的无量纲塑性应变率。
通过试验参数拟合,可以得到相关数值如下:A=325.8、B=487.2、n=0.609、C=0.017,于是HC340LA对应的本构模型为:
3.3 拉伸速率对加工硬化的影响
根据不同拉伸速率得到的真实应力—应变曲线及Hollomon方程[11],得到了HC340LA 单轴拉伸时在不同拉伸速率下的瞬时加工硬化指数,如图5所示。
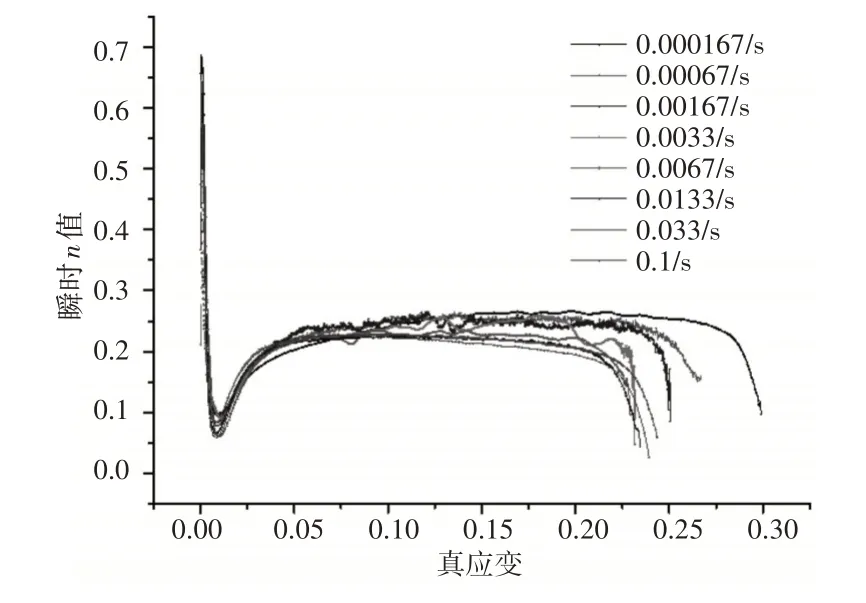
图5 瞬时加工硬化曲线Fig.5 Instantaneous Work Hardening Curve
图中分析结果可知,从0.000167/s的应变速率到0.1/s,材料的瞬时加工硬化指数变化不是很明显,瞬时加工硬化指数在不同的应变速率下整体维持在0.2左右,可见在准静态的应变速率范围内,应变速率对HC340LA的加工硬化影响能力较弱。
4 材料成形极限分析
材料成形极限FLD图,是用来描述材料各路径下最大应变的曲线[12]。通常一条完整的FLD需要6种线性加载路径,如图6所示。它们代表了从单向拉伸应力状态,到平面应力状态,再到等双拉应力状态等成形极限所必须要求的6种应力状态。而凸模胀形实验,就是通过运用不同长宽比的试件,实现多种应变路径,来得到完整的FLD。

图6 FLD所需要的线性加载路径Fig.6 Linear Load Path Required by the FLD
4.1 成形极限试验分析方法
成形极限试样形状,如图7所示。试样各尺寸参数,如表4所示。

图7 试样几何形状Fig.7 Sample Geometry

表4 试样各参数(mm)Tab.4 Sample Parameter(mm)
试样经过试验后的照片,如图8所示。试验中试样的压边力设定为150kN,凸模的运行速度设定为10mm/min。

图8 成形极限试样Fig.8 Forming Limit Specimen
从图8各个不同宽度试样可以清晰的看出开裂位置,几乎所有的试样的破裂位置都是在试样的最顶部,此部位的应变最大。通过应变测试各试样的应变数据,得到材料的FLD曲线,如图9所示。

图9 成形极限图Fig.9 Forming Limit Diagram
FLD0点为试样平面应变特征点,是试验材料在平面应变下的应变极限,此时的e2=0。其大小可以反映材料抵抗破裂的能力,也是FLD上的关键点,从图中可以看出,FLD0约为41%,主要是由于在此应变状态下,材料受到的应力约束较大,变形过程困难,所以达到的极限应变值最低。
4.2 经验公式拟合方法
根据Keeler−Brazier 经验公式[13],可以由经验公式计算得到的FLD曲线。
胀形变形区(次应变e2>0)
拉深变形区(次应变e2<0)
式中:t—材料厚度值;n—平均加工硬化指数,其中式(5)适用于厚度值小于2.5mm 的试样,而式(6)适用于厚度区间(2.5~5.5)mm。
4.3 有限元模拟方法
对成形过程进行有限元模拟实验,有限元模拟实验的板坯厚度t=1.2mm,凸模球头半径rp=50mm,凹模内径D=102.64mm,圆角内径rd=5mm,采用B−T单元划分网格。采用半球形凸模实验方法来获取FLD时,即使润滑足够好,在主要变形区板料和模具之间仍然会发生相对的运动,因此摩擦对这种实验模型的影响是很大的,并且板料所受的摩擦力是随时变化的。
为了与加工过程变化速率保持一致,这里要求凸模冲压速度低于5mm/s。但运用有限元软件进行模拟时,如果冲压速度设置的太小,那么计算所需要的时间会非常久。为了在可接受的时间内完成分析,通常采用较大的冲压速度。一般情况下选择的冲压速度使模型的形变能小于整个模型的能量的10%就是合理的,冲压速度定为1000mm/s。设拉延阻力为300kN,有限元模拟直接采用不同应变速率下的本构方程如式(2)所示,提高模拟精度所搭建的有限元分析模型,如图10所示。
图10 有限元模型Fig.10 Finite Element Model
4.4 不同方案结果对比
通过以上三种方案,获取材料的FLD图,如图11所示。
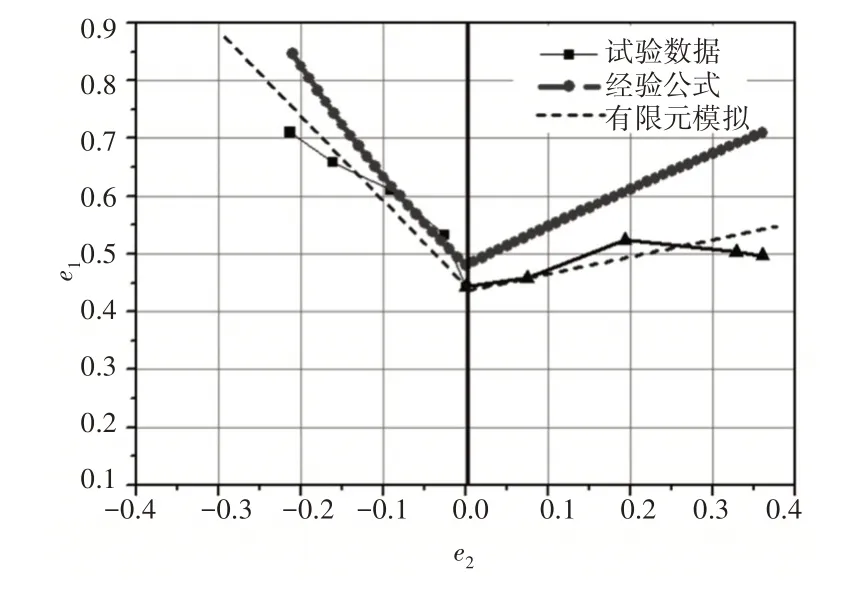
图11 三种方式FLD曲线对比Fig.11 Comparison of Three Ways FLD Curves
从图中可以看出,经验公式拟合得到的FLD 曲线和试验获得的FLD曲线及有限元分析获得的曲线在拉深变形区(次应变e2<0)较为吻合,而在胀形变形区(次应变e2>0)公式拟合与试验获得曲线的差别较大,尤其是在胀形变形区的大应变区,曲线走势不一致,而有限元分析结果与试验曲线变化趋势基本一致。分析原因可能是该经验公式不具有普遍适用性,不能很好的拟合在延展变形部分的成形特点,同时分析FLD试验过程中的各影响因素包括压边力、控制载荷、润滑条件、冲压速度等条件的影响导致最后获取的试验结果也有一定的偏差。同时根据试验测试得到的r值为1.111,说明材料具有较好的成形性能。r值越大,表明在板厚方向上越不易变形,有利于压延成形。
5 结论
(1)应变速率对高强钢HC340LA的强度和塑形都有影响;随着应变速率增大先降低后增大;应变速率对屈强比和平均n值影响很小几乎可以忽略;(2)通过基于Johnson−Cook 模型的高强钢本构方程研究,HC340LA的应变速率敏感性参数C值为0.017,应变速率敏感性较大;(3)在所研究的材料加工过程,由于拉伸速率较低,对加工硬化影响较弱;(4)经验公式拟合和试验获得的FLD曲线及有限元分析获得的曲线在拉深变形区较为吻合;而在胀形变形区公式拟合与试验获得曲线的差别较大,尤其是在胀形变形区的大应变区,曲线走势不一致,而有限元分析结果与试验曲线变化趋势基本一致,应变特征点误差小于3%。结果表明:引入应变速率后结果的准确性明显提升;对成形性的影响不能忽略。

