基于数字孪生的中机身对接装配三维偏差分析
刘娇,惠越,康永刚
(1.中国飞行试验研究院改装部,陕西 西安 710089;2.西北工业大学机电学院,陕西 西安 710072)
1 引言
在飞机从零件到组件再到部件最后到整机的过程中,对接装配质量的优劣直接影响着整架飞机的装配准确度[1]。受自身结构特点、部件刚度低、加工制造误差等因素的影响使得实际部件外形与理论制造模型之间存在一定偏差,该偏差伴随着装配过程产生、传递和累积,影响最终装配的准确度。目前需要寻求一种能够真实反映实际加工制造出来的零、部件偏差与装配最终准确度之间映射关系的方法,实现对最终装配准确度的预测。
在建立公差数学模型及分析方面,国内外学者的研究重点仍是针对零件的设计阶段,对产品尺寸、形状和位置等信息不确定度的简单描述[2−3]。在反映零件制造误差下真实表面模型的几何描述方面,文献[4]基于主成分分析的全局建模法将非理想表面模型用离散数学的方法表达出来。文献[5]在文献[4]工作的基础上将制造误差分为系统误差和随机误差。文献[6]运用小波及谱密度分析方法对非理想表面产品宏微观形貌误差进行了研究。数字孪生[7−9]理念的提出为解决工程实际问题提供了新的思考方向,但基于数字孪生技术的应用仍停留在概念的描述层面。
面向中机身筒段对接装配体,构建了基于数字孪生的三维偏差分析模型,为大部件对接装配过程提供了姿态优化调整的参考数据与参数,实现了实际工况下装配偏差的准确预测。
2 中机身对接模型构建
采用激光轮廓传感器,获取部件表面外形数据,结合工业相机,获取部件上的关键特征点的位置信息,配备一套三个坐标轴的转动角位移台、三个坐标轴的平动位移台用于控制部件的六个方向自由度,真实反映筒身调姿对接过程的实际工况,如图1所示。图中的关键目标点为两端面特征x方向之间的装配间隙。

图1 筒体对接测量与调整结构示意图Fig.1 Schematic Diagram of Barrel Butt Joint Measurement and Adjustment Structure
3 数字孪生模型构建
3.1 数字孪生模型
基于数字孪生的装配分析不同于以往产品公差设计,具体区别,如图2所示。随着数字孪生概念的提出以及现代先进测量技术的发展,可通过三维数字化测量设备获得较高精度的零件表面数据,构建能够一一映射零件的真实状态信息的数字孪生模型,以数学分析的方法预测实际工况下的零件装配完成后的关键特征点的精度。

图2 数字孪生装配体偏差分析Fig.2 Deviation Analysis of Digital Twin Assembly
采用新一代产品几何技术规范(Geometrical Product Specifi⁃cation,GPS)标准体系,对数字孪生下的零件特征进行定义。其中,新一代GPS中给出了表面模型的概念,它是各阶段规范表达的基础,选定其中获取认证表面模型[10]的思想理念,作为用于反映实际状况下几何量变化的数字孪生模型建立的指导方法,通过分离、提取、滤波、拟合四个操作步骤实现模型的构建。
主要通过高精度三维扫描设备获取实际工况下零件表面上的采样点数值,对这些离散点进行上述四个步骤的处理,将关注的非理想特征以理想特征的形式表示出来,从而得到可以用于偏差分析的数字孪生模型,实际建立过程,如图3所示。

图3 用于偏差分析的数字孪生模型建立过程Fig.3 The Process of Establishing the Digital Twin Model for Deviation Analysis
3.2 圆柱面拟合算法
3.2.1 圆柱面数学模型构建
根据圆柱面的几何特征,对圆柱模型进行构建,需要7个参数,分别为圆柱中心轴线的方向向量(a,b,c)和中心轴线上的某一点坐标(x0,y0,z0),以及圆柱的半径r,因此得到圆柱面数学模型为:
参数拟合的过程即为估计(x0,y0,z0,a,b,c,r)这7个参数。
3.2.2 柱面拟合效果实验验证
对样件进行测量,采用RANSAC算法拟合初值,之后采用最小二乘算法对剔除离群点后的测量数据进行拟合实验,如表1所示。利用残差对拟合结果进行评价,如图4所示。可以看出整体残差分布均匀,大部分测量点集中在(±0.1)mm内,且对于离群点较多的测量数据具有较好的稳健性,该算法适用于圆柱面拟合。

图4 柱面拟合结果与残差统计直方图Fig.4 Cylindrical Fitting Results and Rresidual Tatistiscal Histogram

表1 圆柱面模型参数拟合结果Tab.1 Fitting Results of Cylinder Model Parameters
可以看出整体残差分布均匀,大部分测量点集中在(±0.5)mm内,且对于离群点较多的测量数据具有较好的稳健性,说明该算法适用于圆柱面拟合。
3.3 平面拟合算法
3.3.1 平面数学模型构建
3.3.2 端面拟合效果实验验证
对样件端面外形进行标识点测量,使用奇异值分解来求解待定参数的整体最小二乘解,得到部件模拟样件的端面模型参数(A,B,C,D),如表2所示。利用残差对拟合结果进行评价,如图5所示。可以看出,整体残差分布均匀、大部分测量点集中在(±0.1)mm范围内,说明该算法适用于平面拟合。

表2 平面模型参数拟合结果Tab.2 Fitting Results of Plane Model Parameters

图5 平面拟合结果与残差统计直方图Fig.5 The Plane Fitting Results and the Residual Statistical Histogram
4 基于数字孪生几何装配体的三维偏差模型构建
4.1 中机身部件位姿计算
制造误差使得部件端面与部件轴线之间存在一定的夹角,为获得实际制造误差下部件端面与部件轴线之间的姿态的变动量,需要将端面姿态与柱面姿态绑定,即重新定义中机身部件拟合后的局部坐标系,如图6所示。

图6 部件局部坐标系定义Fig.6 Part Local Coordinate System Definition
设部件轴线的方程为:
联立端面方程得到轴线与端面的唯一交点O1(x1,y1,z1)的坐标值,该点为部件拟合后局部坐标系原点。P为部件端面上关键目标点,将其坐标统一到全局坐标系下,根据坐标之间的转换关系,得到局部坐标系到全局坐标系的旋转和位移。结合偏差分析模型式(4)、式(5)用于描述零件几何特征之间的变动关系及传递方式。
4.2 软件平台开发
在Visual Studio 2013 开发环境下,基于MFC 编程框架进行开发,平台主要由圆柱面拟合模块、端面拟合模块、装配体偏差计算模块组成,系统界面及实现流程,如图7、图8所示。
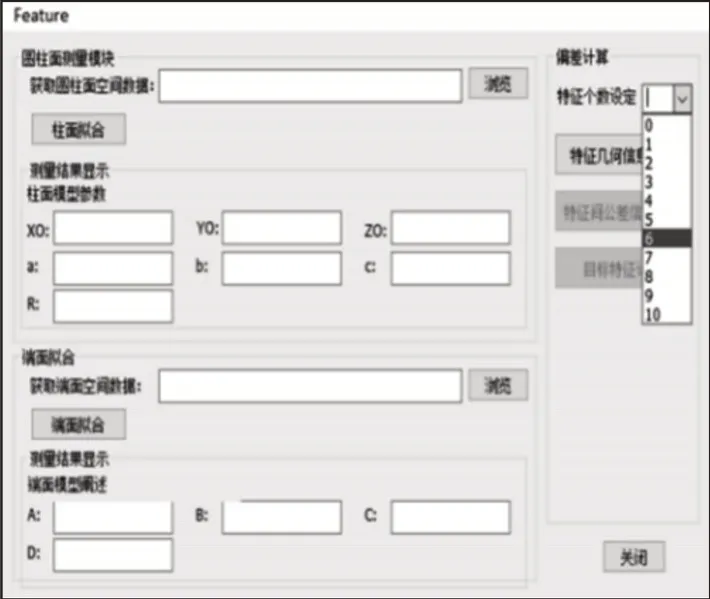
图7 软件界面Fig.7 Software Interface
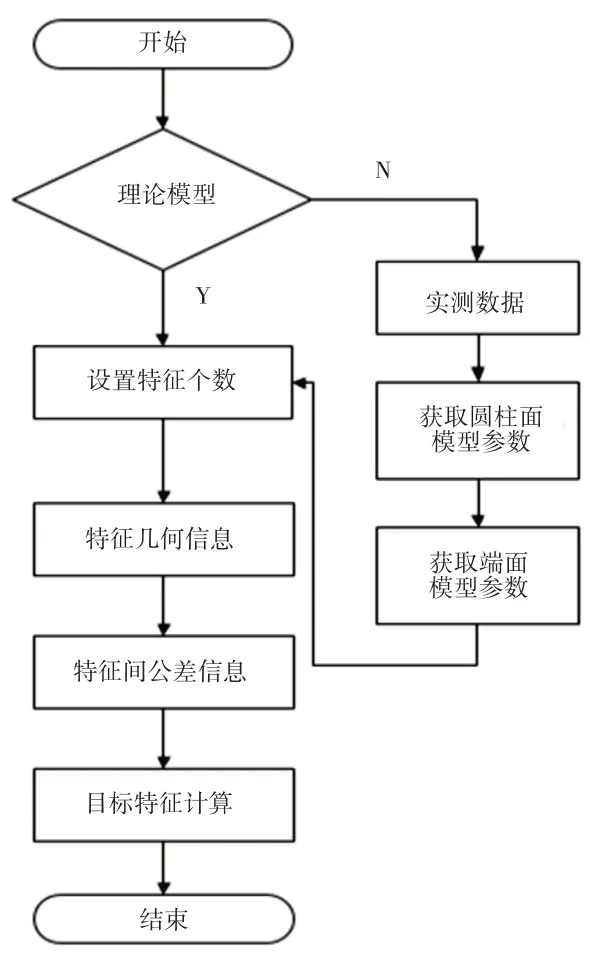
图8 系统功能实现流程Fig.8 System Function Realization Process
5 建模分析正确性验证
5.1 3DCS仿真分析
以国际上专业用于偏差分析的软件3DCS 的计算结果为标准,验证本文软件系统偏差预测分析结果的正确性。
通过输入零件几何模型信息、零件公差信息、定义装配顺序和定位方式、设定产品装配测量关键目标,最终获得关键特征的装配偏差,如图9所示。

图9 3DCS偏差分析结果Fig.9 3DCS Deviation Analysis Results
根据本文提出的方法,计算结果,如表3所示。

表3 偏差计算结果Tab.3 Deviation Calculation Result
5.2 结果比对
由于关键目标点为两端面特征x方向之间的装配间隙,从表中可以看出x方向的变动范围为:x=±1.1857mm,即[182.1143,184.4857]mm。以仿真分析结果为标准,比对发现计算结果有92%的偏差落在标准变动范围内,认为该方法具有一定的可行性,即验证了方法的正确性。
经过分析,导致结果存在一定偏差的因素有:
(1)在实际测量过程中存在测量误差,因此存在新的偏差源带来的干扰。
(2)在拟合过程中,测量数据点的选取对拟合算法本身存在一定的影响。
6 结论
提出的数字孪生模型的偏差分析系统的应用具有以下优势:
(1)基于数字孪生装配体的分析,采用实测数据通过计算部件的外形几何参数,与理论模型对比,能够在对接装配开始前,分析部件的制造准确度是否满足对接装配要求,达到了预装配分析的目的,减少了人工参与次数,提高了对接装配效率。
(2)对关键特征偏差的计算过程简单运行次数少,从而可以大大减少现有的装配分析次数,提高了装配效率。
(3)端面拟合模块和柱面拟合模块的生成的参数数值,结合角度转换公式,为大部件对接过程姿态优化问题提供了优化参量和调姿依据,有效控制了对接装配质量。

