在问题探究中“生长数学”——以《一次函数》期末复习课为例

代 影

(江苏师范大学附属实验学校，江苏 徐州 221011)

卜以楼老师提出的“生长数学”理论，从凸显教育价值、塑造核心素养、营造思维必然、创设意识唤醒等多方面，提出了数学系统教学与素质思维培养的重要性，强调数学课堂实践应找准知识生长点，选好生长路径，教给学生具有生长力的数学.下面以苏科版教材《一次函数》期末复习课为例，借助问题引导教学手段，探讨一下课堂教学如何探寻数学知识生长点，引领学生构建知识结构体系.

1 “生长数学”下的问题提出

《一次函数》是初中阶段“数与代数”中的重要教学内容.它既是学生接触“函数”的起始，也是后续学习的基础.本节授课对象为初中八年级学生，所用教材为苏科版数学八年级上册教科书.本节为期末复习课，倘若在教学中仅限于单元内容回顾，拘囿于教材章节编设框限，则不利于学生整体知识体系构建，更不利于创新思维与数学能力培养.笔者在本课执教过程中进行了以下思考：《一次函数》作为初中“数与代数”的重要衔接内容，如何向内充分发掘其内涵、向外充分拓展其外延，让学生在知识生长中自然厘清其内在关联，自觉建构完整数学知识体系，在学会数学知识的同时有助于其数学素养发展.

2 “生长数学”下的教学研判

2.1 学情分析

学生学习本章后已初步掌握了一次函数概念、性质与运用等相关知识，能根据函数关系画出图像或根据图像确定函数解析式，对具体问题中函数变量之间的关系也具备初步分析能力.由于初次接触函数，学生对函数的理解程度有待加强.对一次函数所蕴含的“由数到形”或“从形到数”的数学思维认知有待深入.

2.2 目标设定

临近学期结束，学生章节学习情况尚可，但期末复习需对全册数学知识融会贯通，将全册数学知识以整体化视角进行综合构建.基于上述考虑，笔者对本节复习教学设定如下目标.

2.2.1 教学目标设定

(1)了解一次函数的形式、图像及性质，能灵活运用一次函数解决数学问题.

(2)借助具体数学问题，进一步理解“分类”“数形结合”“几何直观”等数学思想方法，提升学生数学综合能力.

(3)对本章涵盖的数学知识与方法进行系统梳理，使其结构化，发展数学经验.

2.2.2 本课教学重点与难点

重点：一次函数的数形结合应用.

难点：章节知识体系构建，理解分类数学思想，用函数与方程解决数学问题.

3 “生长数学”下的教学设计

3.1 以问题建构知识网络

师：临近期末，本节课我们一起来复习一次函数.复习之前，通过一道题让大家回顾一下一次函数.

问题1下列函数：(1)y=x；(2)y=2x-1；(3)y=1；(4)y=1002-3x；(5)y=x2-1中，是一次函数的有( ).

A.4个 B.3个 C.2个 D.1个

生1：选项(3)y=1，没有自变量x，选项(5)y=x2-1，x是二次幂，只有(1)(2)(4)符合一元一次函数概念的要求.

师：学生1回答得很好.借助这道题，大家回顾一下什么是一次函数？

生：(集体思考，回顾章节知识)

【设计意图】引导学生回顾函数、变量、一次函数的概念与内涵，为生成数学奠定知识基础.

问题2已知点A(0,6)与点B(8,0)是一次函数y=kx+b图像上的点，试求出这个一次函数的具体表达式.

师：回答得很好.大家能否画出这个一次函数的图像.

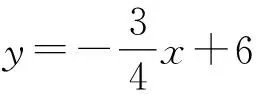
【设计意图】引导学生回忆一次函数y=kx+b(k≠0)的图像及性质，将一次函数与其特例正比例函数关联起来，引发学生数形结合地思考.

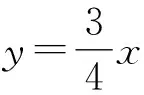
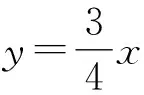
师：非常好！很好地运用了“一元二次方程与一次函数”的关系.还有其他解法吗？

生5：我觉得可以用画图解决.(上台示意，见图1).

图1

师：生5给出了另外一个解题思路：图像法.大家还记得我们在学习二元一次方程组与一次函数的关系时，提到用一次函数来解决二元一次方程组的话，通常采用什么方法？

生：图像法.

【设计意图】启发学生对章节内容进行系统回顾与整理，帮助学生形成数学知识系统.

3.2 以问题生长数学思维

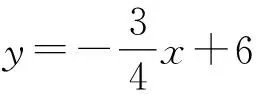
生6：可以用两点间距离公式计算，答案为10.

师：很好，两点距离公式可求平面直角坐标系内任意两点间的距离.还有什么其他解法吗？

生7：我觉得可以用图像法求解，根据题目条件，可求出A、B两点坐标分别为(0,6)、(8,0).画图(见图1)可知，△AOB为直角三角形，根据勾股定理，可计算出斜边AB=10.

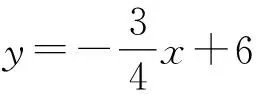
生：(纷纷举手，在台下喊)用图像法，用等积法.

【设计意图】助函数表达式建构图像，培养学生“数形结合”解题思维与习惯，是一次函数教学的重要任务.

问题5假设一次函数y=kx+b中自变量x的取值范围为-2≤x≤6，其对应的函数值范围为-11≤y≤9.求该函数的解析式.

师：大家觉得生8的解法怎么样？有没有什么补充？

生9：老师我认为他的思考不全面，他只考虑了函数值y随x变大而变大的情况，即k>0的情况；而y随x变大而减少，即k<0的情况他没有考虑到.

师：应该怎么做？

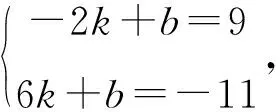
师：这种解题思维也被称作为“分类”思想.布置一道课后思考题，想想会有几种情况出现，考查一下大家对“分类”思想的应用.

问题6直线y=4x+6与x轴交于点A，与y轴交于点B.过点B作直线BP与x轴交于点P，且使OP=2OA，求△ABP的面积.

【设计意图】对一次函数系统知识的深化与构建，同时也引出了对数学解题策略中“分类思想”的教学渗透，体现了生成数学对学生数学思维培养的重视.

卜以楼老师指出：“生长数学”是前后一致、逻辑连贯、一以贯之.“生长数学”理念的运用促使学生将过往学习经验与新学知识应用融于一体，体现了对学生数学整体知识的梳理与体系建构，对培养学生数学思维与能力生长创设了积极条件.借助复习课形式，如何体现“生长数学”纲举目张、前后贯通等教学要求，促使学生学习能力与素质得以全面提升，值得每位教师深刻思考.