引导学生在感悟中学习数学

耿 征

(徐州市第十三中学，江苏 徐州 221000)

1 发现问题

例1 已知xm=2，xn=5，求xm+n的值.

学生做法：因为xm=2，xn=5

所以xm+n=xm+xn=2+5=7

正确做法：因为xm=2，xn=5

所以xm+n=xm·xn=2×5=10

2 提出问题

为什么学生知道本题是逆用同底数幂的乘法法则，但逆用的过程却出错呢？

3 分析问题

幂的四种运算：

(1)积的乘方 (ab)n=anbn

(2)幂的乘方(am)n=amn

(3)同底数幂的乘法am·an=am+n

(4)同底数幂的除法am÷an=am-n

幂的运算法则的应用，主要关注的就是指数之间的进行运算.

幂的四种运算法则的逆用：

(1)积的乘方anbn= (ab)n

(2)幂的乘方amn=(am)n

(3)同底数幂的乘法am+n=am·an

(4)同底数幂的除法am-n=am÷an

幂的运算法则的逆用过程，只有幂之间的乘除关系，没有加减关系.

学生之所以出现错误，原因就在于对幂的运算法则的理解缺少感悟——没有明确幂运算法则的逆用只有乘除关系，没有加减关系，如果学生理解这一点，错误就不会发生了.

《义务教育数学课程标准》指出：数感主要是指关于数与数量、数量关系、运算结果估计等方面的感悟；关于“零指数”教学方案的设计可作如下考虑：教学目标不仅要包括了解零指数幂的规定，会进行简单计算，还要包括感受这个规定的合理性，并在这个过程中学会数学思考、感悟理性精神；学生在积极参与教学活动的过程中，通过独立思考、合作交流，逐步感悟数学思想.

教师的引导作用主要体现在：通过恰当的问题，或者准确、清晰、富有启发性的讲授，引导学生积极思考、求知求真，激发学生的好奇心.

由此可见，在数学教学过程中，我们不能轻易放过出现的问题，不能轻易放过学生提出的疑问，而是要带领学生及时对出现的问题、产生的疑问反思，找出问题的根源、疑问的解决方法，这就是对数学的感悟.

4 解决问题

4.1 增强对数学定义的感悟能力——看破本质

例2 分解因式6a(1-b)2-2(b-1)2

学生做法：6a(1-b)2-2(b-1)2=(1-b)2(6a-2)

教师引导过程：

教师：这位同学的做法错在哪里？

学生：(6a-2)没有分解完.

教师：那应如何继续分解？

学生：(6a-2)=3 (3a-1)

教师：为什么会出现这种错误呢？

学生：应该一开始就提取公因式

教师：所以正确的做法应该为？

学生展示：6a(1-b)2-2(b-1)2=6a(b-1)2-2(b-1)2=2(b-1)2(3a-1)

教师：正确!请大家继续思考，如何避免类似错误再次发生？

学生：……

教师：因式分解的结果要求分解到不能再分解为止，所以建议大家每次因式分解结束，请一定要检查，是否分解到位！尤其是公因式是否提取完整！

学生没有分解到位，而这也是学生最容易犯的错误.学生之所以没有分解到位，表面上是因为公因式提取不完整、不全面，而深层次的原因是对因式分解概念本质理解的不清晰.

因式分解是指将一个多项式写成整式乘积的形式，而因式分解的结果有三个要求：

(1)结果必须是乘积形式；

(2)结果每一项必须是整式；

(3)结果每一项必须分解到不能再分解为止.

这三个要求就是对因式分解本质的解读.上述案例出错的原因是没有达到因式分解的结果的第三个要求.

因此在教学过程中，引导学生每次分解结束，要检查结果是否分解到位；先考虑提取公因式，而公因式先要考虑系数.

4.2 增强对数学定理的感悟能力——逆向思维

例3如图1，直线AB、CD被直线EF所截，∠1=75°，下列说法正确的是( ).

图1

A.若∠4=75°，则AB∥CD

B.若∠4=105°，则AB∥CD

C.若∠2=75°，则AB∥CD

D.若∠2=155°，则AB∥CD

学生思路1：先看A选项，因为∠4=75°，所以∠3=105°，但∠3≠∠1，所以AB不平行于CD.依次类推，选择B

学生思路2：由AB∥CD，∠1=75°，可以得到∠2=∠3=75°，∠4=105°，从而确定B正确.

两种思维过程都是正确的，思路1是多数学生会想到的，是学生做题一般的思维过程.但为什么思路2也可以得到正确答案呢？因为“两直线平行，同位角相等”与“同位角相等，两直线平行”是一对互逆真命题，故可以逆向思考.

初中几何结论中，还有很多互逆真命题，像勾股定理及其逆定理，直角三角形两锐角互余与两角互余的三角形是直角三角形等等，教师要及时引导学生建立互逆命题之间的联系.

在具体解决数学题时，也可以引导学生进行逆向思考.

例4如图2，在ABCD中点O是边BC的中点，连接DO并延长，交AB延长线于点E，连接BD，EC．

(1)求证：四边形BECD是平行四边形；

(2)若∠A=50°，则当∠BOD为多少时，四边形BECD是矩形．

图2

在解决第(2)个问题时，可以考虑先假设四边形BECD是矩形，逆向推出∠BOD的度数.

4.3 提高对数学图形的感悟——比较还原

例5已知，∠AOB=90°，点C在射线OA上，CD∥OE．

(1)如图3，若∠OCD=120°，求∠BOE的度数；

(2)把“∠AOB=90°”改为“∠AOB=120°”，射线OE沿射线OB平移，得O′E，其他条件不变，(如图4所示)，探究∠OCD、∠BO′E的数量关系；

(3)在(2)的条件下，如图5，作PO′⊥OB垂足为O′，与∠OCD的平分线CP交于点P，若∠BO′E=α，请用含α的式子表示∠CPO′(请直接写出答案)．

图3 图4 图5

学生思路：

(1) 因为CD∥OE，所以∠EOC=∠OCD=120°,所以∠BOE=360°-∠EOC-∠COB=150°

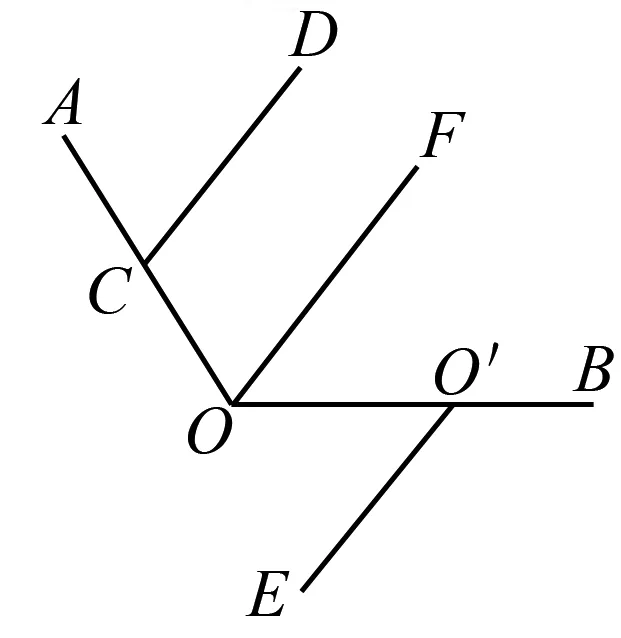
图6

(2)如图6，过O作OF∥CD，那么OF∥OE′，

所以∠COF=180°-∠OCD，∠FOB=∠OO′E

所以∠COF+∠FOB=180°-∠OCD+∠OO′E=∠AOB=120°,即∠OCD-∠OO′E=60°.

又因为∠OO′E=180°-∠BO′E,

所以∠OCD+∠BO′E=240°.

可以看出，学生把前两个图形孤立来看，两幅图两个思考过程.这无形增加了思维量，也降低了解题效率.

引导过程：

教师：请同学们仔细观察，图4与图3比较，哪里发生了变化？

学生：射线OE的位置，∠AOB的大小.

教师：通过你们的做法，可以看出∠AOB的大小，不影响思考过程.那么射线OE位置的改变，导致你们思维过程的变化.那能否还原O′E的位置到OE′)呢？

学生：平移不改变图形的大小、形状.也就不改变∠BOE的大小.(这就是感悟的过程)

教师：说的很好，这就是关键！当还原OE后，是否借助第(1)问的思维过程进行书写？

学生：可以发现，∠E′OC=∠OCD,

那么∠EO′B=∠E′OB=360°-120°-∠OCD=240°-∠OCD

教师：很明显，既简化了思维过程，也简化了书写过程.

教师：请同学们继续思考，前两问产生了联系，那么第(3)问呢？

学生：可以将结论∠OCD、∠BO′E的数量关系直接应用到.

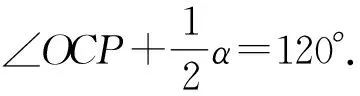
利用四边形COO′P内角和为360°，就可以用含α的式子表示∠CPO′.

教师：讲解正确.确实将发现的结论可以直接利用来解题.

总之，在数学教学过程中，既要时时刻刻关注学生出现的问题，又要时时刻刻对自己的教学进行反思，在感悟中提升，在感悟中进步.