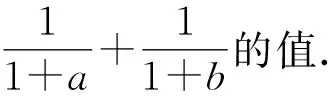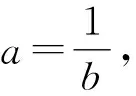初中数学解题中常见错误成因及应对策略
赖智勇
(福建省上杭县古田中学,福建 龙岩 364201)
小学与初中两个阶段的数学学习方法存在着较大的差异,部分学生进入初中之后,显得十分不适应,在数学解题中答频繁出错.作为初中数学教师,应当从常见的初中数学题型着手分析,了解学生常见的解题错误原因,分析题目的解题方法,减少学生解题失误,以提高学生的数学学习成绩.
1 初中数学解题教学存在的问题
其实在数学学习过程中,学生解题错误是不可避免,而教师对待学生错误的态度将会影响学生的数学学习效率.然而,在初中数学教学中,部分教师对学生的学习情况不够了解,并没有帮助学生正视自己解题错误的原因,没有从积极鼓励肯定的角度给予学生更多的学习帮助.如果教师没有深刻分析学生解答数学题目时存在的错误原因,不能帮助学生找到解题错误的原因,那么学生的解题效率是不可能得到有效提升的.
2 初中数学解题中常见错误成因
2.1 小学学习习惯影响
初一的学生在数学解题过程中容易出错,主要是受到小学阶段的学习习惯、学习方法的影响.而由于初中和小学两个阶段的数学学习是存在较大差异的,如果学生采用小学的数学学习方式、解题方式,可能会导致学生在解答初中数学题目的过程中存在一些错误思维,影响学生的解题正确性.甚至学生在小学数学学习过程中形成的一些定势思维,会妨碍学生对初中数学基础知识的深度学习,让学生对题目的理解产生错误.
2.2 学生解题粗心大意
部分学生解题习惯不好,在解答题目的过程中粗心大意,会造成题目信息阅读不全、审题不清等问题.这种不良的解题习惯导致学生在数学题目阅读的过程中会漏掉关键的题目信息.比如看错题目中的小数点、运算符号或者题目中的数字信息等等,这些都是粗心、马虎造成的解答出错.因此,教师应当加强学生的解题方法的训练,解题习惯的培养,帮助学生克服粗心、马虎问题,以严谨的态度对待初中数学学习和题目的解答.
2.3 基础知识不扎实
还有部分学生是由于对所学习的数学知识掌握不扎实而导致出错.首先,学生基础知识掌握不扎实,在解题的时候就时容易出现概念方面的错误,导致解题出现问题.特别是一些复杂的概念容易混淆,使学生出现张冠李戴现象,导致没有办法找准解题的突破口;其次,有些学生选择死记硬背的方式进行数学概念的学习,没有深层次理解数学概念内涵,在解题时就不能对知识灵活应用,解题出错就在意料之中了.
3 初中数学解题错误的应对策略
3.1 帮助学生正视解题错误
首先,教师应当正视学生的错误问题,引导学生从方法上正视自己数学题目的错误原因,继而培养学生良好的数学学习习惯.在初中数学教学过程中,教师要重点关注学生核心素养的培养与提升,使学生养成良好的学习习惯.教师切记不可在学生出现解题错误的时候,对学生进行严厉的批评和指责,这会给学生带来严重的心理压力,会导致部分学生丧失数学学习的自信心.反之,教师应该给予学生更多的耐心指导与讲解,让学生明白数学解题过程中需要注意哪些方面的问题,帮助学生自提高解题能力,这个过程可以让学生享受到数学学习的快乐.
其次,教师应当引导学生正确认识初中和小学的数学解题的区别,帮助学生树立良好的数学学习思维.例如小学学习的过程中,对“5-8”这个式子的理解,学生对“-”的认识,仅限于减法.而学习了初中数学之后,学生可以理解成减号与负号.因为减去一个数就等于加上这个数的相反数,这就是小学和初中数学的一个显著区别,而学生不能再局限于小学的数学解题思维中.
再次,教师要有足够的耐心,并且站在学生的角度,帮助学生解决掉解题过程中的困惑,使教师和学生之间的距离更贴近.当学生成功克服了一个又一个的数学难题之后,能感受到解答困惑的喜悦,从而产生数学学习的热情,在潜移默化中提高学生的数学解题能力.
例如,如图1,已知△ABC是等腰三角形,AC=BC,AC⊥BC,CD⊥AB,求证∠ACD=∠BCD.
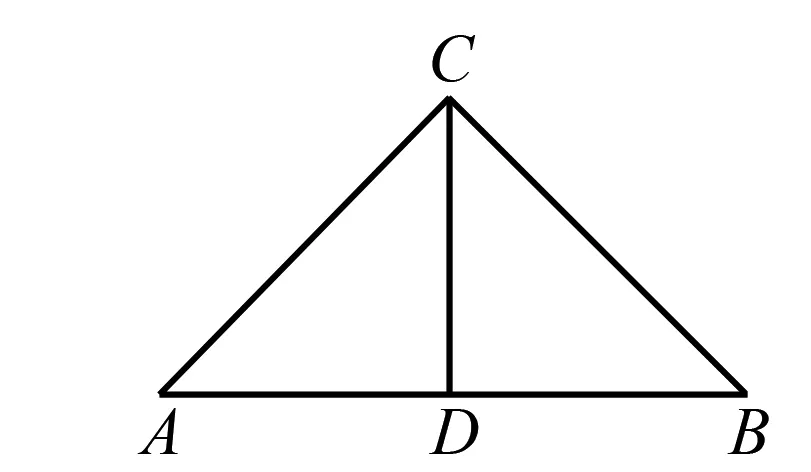
图1
在这个题目的解答中,教师应该从学生的数学基础知识角度做出分析,帮助学生进一步夯实基础知识,让学生深刻理解这道题目所考查的内容.从题目的已知信息可以看出,这道题目考查了三角形相关的概念,根据等腰三角形性质,题目信息AC=BC,结合垂直信息,得到∠A+∠ACD=90°=∠ACD+∠BCD,所以得到∠A=∠BCD,同理,得到∠B=∠ACD,在等腰△ABC中,因为∠A=∠B,所以∠ACD=∠BCD.根据题目中的已知条件进行论证推理,需要学生熟练掌握等腰三角形和直角三角形的基础知识,只有基础知识掌握扎实了,解题才会得心应手.
3.2 加强解题方法培养
在初中数学教学活动的开展中,教师需要帮助学生掌握学习多样化的解题方法,拓展学生解题思路,减少学生的解题错误,提高学生的解题信心,以此加强学生良好行为习惯的养成.数学学习是一个循序渐进的过程,由于数学学习过程中知识结构不深化,学生的认知发生了较多的变化,采用多样化解题方法能有效解决解题错误问题.
例2已知如图2,在四边形ABCD中,AB 图2 解因AB 在△BAD和△BED中, 因为BA=BE, ∠ABD=∠EBD, BD=BD, 所以△BAD≌△BED(SAS), 所以AD=ED, ∠A=∠BED. 又因为∠A+∠C=180°, ∠BED+∠DEC=180° 所以∠C=∠DEC, 于是ED=CD, AD=CD. 在这道题目的解答过程中,教师应该重点关注解题方法、解题思维的引导,让学生理解角平分线的辅助线构造.在平面图形的解答过程中,如果发现题目有角平分线,通过构造全等三角形的方法可以促进题目的解答完成.因为角平分线两侧存在一组相等的角,通过这样的造方式,再构造出一个合适的等价条件,就能证明三角形的全等.在三角形的教学过程中,教师除了引导学生学习角平分线的构造,还可以引导学生进行垂线构造法、中位线的构造法、中线构造法等等,从而更好完成题目的解答. 当学生在进行数学题目作答的时候,教师可以对学生常见的错误问题,通过范例分析的方式,引导学生发现数学解答过程中存在的问题,了解存在的错误原因,比如学生常见的数学概念理解不清、隐含条件没有把握住等等.通过案例展示可以避免更多类似错误情况的发生,使学生在解题操作中,将自己存在的错误原因进行反思并归纳总结.因此,这种教学模式可以帮助学生对自身错误原因进行深化认识,找到学习过程中的薄弱点,从而帮助学生提高数学的解题能力. 代入原式,得到 在这种代数求值问题中,教师就应进行分类教学,考虑如果题目没有给出a≠-1这个条件,那么就不能直接用这样的代数消元法进行题目的解答了,需要考虑不同的情况,以分类讨论的形式进行题目的. 综上所述,为了培养学生良好的解题习惯,锻炼学生的解题能力,初中数学教师应当关注学生在数学题目解答过程中常见错误的成因,并且整理归类,帮助学生树立良好的解题认知体系,形成良好的解题判断思维,从产生错误的根本原因着手分析,加强日常解题锻炼,提高学生的综合解题能力.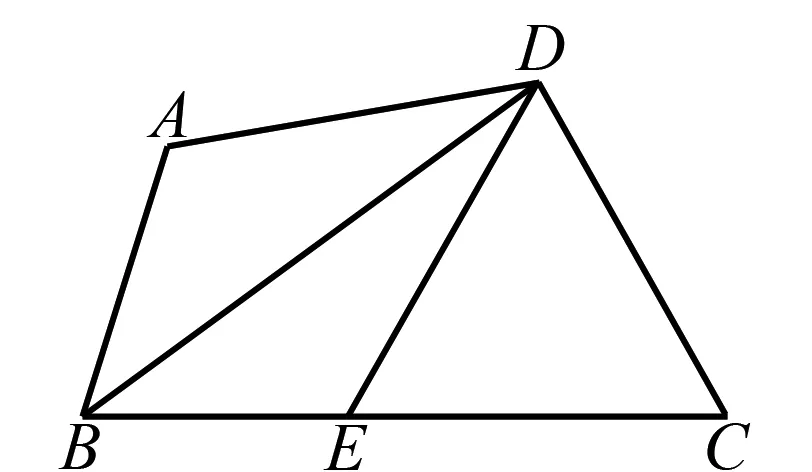
3.3 加强范例教学的应用