数形结合思想在初中数学解题中的应用

林明霞

(福建省莆田市秀屿区实验中学，福建 莆田 351100)

1 数形结合思想的内涵

“数”与“形”是初中数学教学过程中最为基本的两个概念.数形结合的思维运用其关键就是通过数量和图形相互结合，促进学生对数学解题有更加深刻的解题思维.数形结合需要将数学定理、公式与图形相结合，并引导学生对数学问题进行思考.在日常的教学过程中，普遍使用的教学形式主要表现在用数来研究图形与用图形来研究数，根据教学形式的不同分为了“以形助数”与“以数解形”两个方面.在初中数学中，数量问题主要分为代数问题、函数问题、集合问题等.在初中数学的解题步骤中要运用好数形结合的思想,将抽象的数量问题转化为具体的图形问题,或者将直观的图形转化为准确的数量.

2 数形结合思想在初中数学解题中的意义

2.1 培养学生的解题兴趣

初中数学题目涉及逻辑和思维，难度大，初中学生在数学解题过程中感到枯燥乏味，容易导致学生失去学习的信心.在日常教学过程中，教师要充分调动学生对数学这一课程的学习欲望，教师要对自身的教学观念进行不断更新.比如教师在教学过程中引入图像的表现方式，将二次函数以形象化的方式表现出来.同时可以结合互联网PPT对教学图像进行展示，从而达到吸引学生学习二次函数的欲望，激发学生对数学的学习热情，也实现了使学生在学习数学的解题思路中快乐学习的教学初衷.

2.2 发展学生的解题思维

初中数学的难度随着知识的深入不断加大，很多学生在解题过程中出现困难.数学解题过程中需要大量的思维能力，通过对数学问题的本质的剖析，数量关系与图形能够相互转化和补充，让学生能够快速把握问题的关键，并对题意有了更加深刻的印象，解题的思路也变得更加清晰，从而提高学生在数学问题中的审题与解题能力，拓宽了学生思维的发展.例如，在教授运用几何方法解决代数问题的课程时，教师可以通过代数与几何图形的关联度，剖析二者共同点，寻找到科学的解决方案，提高学生的逻辑思维能力.

2.3 提升学生的解题能力

数形巧妙结合的思想含义是通过两个数形概念之间存在的关系进行深入分析，同时对几何空间、数量关系等进行一个巧妙的结合,从而逐步找到一些解题方面的头绪,让许多问题可以从复杂变得更加清楚简单,最终得到解决问题的方案.初中数学教学中比较常见到的几何代数问题，就可以借助直角三角形、矩形、椭圆等解决.例如,可以考虑借助直角三角形来解决所有与勾股定理紧密相关的代数问题.

3 数形结合思想在初中数学解题中的应用

初中数学知识的基本概念有着抽象性的特点，导致学生对基本概念的理解容易产生偏差，影响了学生数学解题能力.比如:求得出任何一个二元一次方程和其中任意一个一元一次二方程间的正交点的坐标.在教学过程中,要让学生自己先以画图的解题思维方式，在一个坐标系图中画出表示两个方程式交点的一个函数图像,并能够在这个函数图中找到这两个方程式交点坐标.而在“以形助数”的教学过程中，要通过图像将抽象的数学概念正确地表达出来，图像还要表现出数字与数字之间的异同关系.例如，学生在解一元二次不等式时，可以直接将代数代入进行运算，但存在解题时间长、解题思路混乱的问题.通过图形可以充分解决一元二次不等式的这些问题，将不等式两边分别看做是一元一次方程和一元二次方程，并把两个方程的以图像的方式在坐标系中画出，同时根据不等式的方向，选择与方程有交集的图像，而不等式的解集便是被截取的那一部分.综上所述，数形结合的解题方式对学生了解初中数学解题思路有着极大帮助.

3.1 数形结合解决概念问题

初中数学概念的课程教学设计目标，不仅强调要让广大学生了解数学的基本概念,还要对其含义形成初步的正确理解.教师们必须反复对数学的教学理论进行分析，通过比对、总结和归纳概括三个环节,对数形结合相关概念论证的完整逻辑过程进行了详细的解析,让所有学生从中感知了解每个数学概念背后蕴含的数学思想.

3.2 数形结合解决函数问题

在初中数学课程设计中，往往会遇到学生对典型的函数问题或复杂型函数问题的主要概念性质关系无法正确理解.函数问题研究其实是一个包含各种简单代数知识内容与微分几何知识内容的有机数学综合体.教师在数形结合的教学基本思想中可以使用“以形助数”的教学思维方式.例如,小东正在击打羽毛球,其中小东的实际身高约为1.25m，且只能以直线高度BC来予以表示,而此时当他进行击打后，打飞出来后的羽毛球的实际最高直线飞行点的直线高度则恰为2.25 m,此时若羽毛球与小东的实际水平距离正好约为1 m,那么羽毛球实际的直线最终的拍落点A和小东的实际垂直距离应是约有多少米长?这个数学问题同样也有涉及到了关于“抛物线”知识中的“应用型函数”的一个知识点.通过图1我们可以很清楚准确地看到,题目主干信息是所要求函数的所求B点到函数所求的A点之间的一条直线距离,通过这个图，学生们可以对该函数题干信息整体有了一个更加清晰和直观地了解.

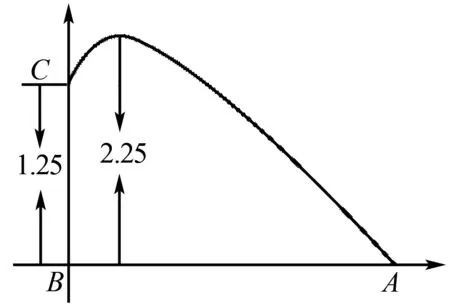
图1

3.3 数形结合解决不等式问题

“不等式”是初中数学教学过程中重要的的一个知识点，在解一元一次不等式的过程中要注意两点：第一是未知数前面的系数是负数时，当系数化1 后，不等式的不等号要变方向，“>”要变为“<”；第二是“≤、≥”表示实心，“>、<”表示空心.

如图2，在求不等式的解集时，为了清楚地得到不等式在数轴上的解集，重点在于x<1是空心，x≥-2的方向, 因而选择B.

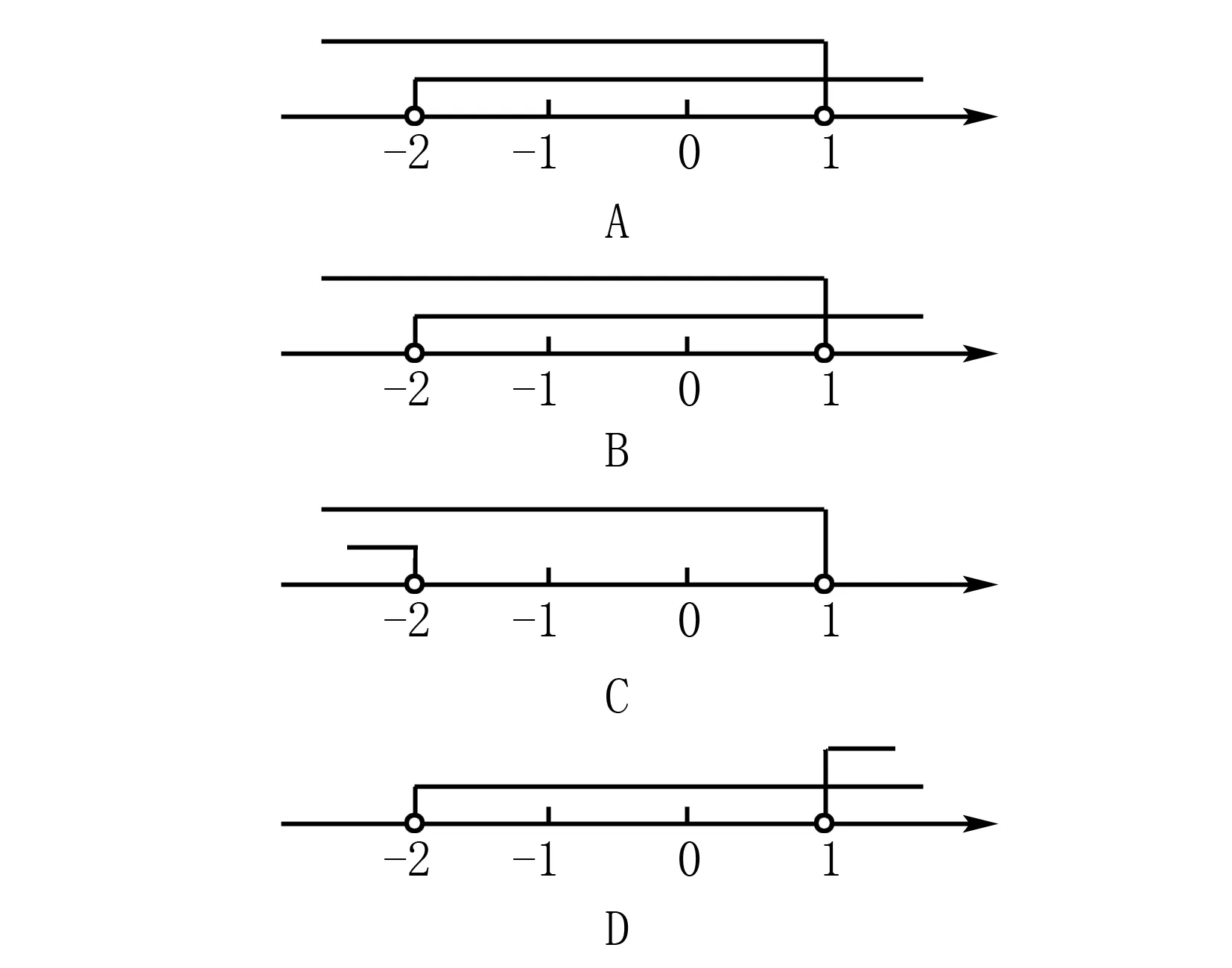
图2

利用数轴也可以解决找众数和中位数的问题，众数是指所有变量中出现次数最多的数值，中位数是将各个变量按大小的顺序排列后，处于中间的变量值.

3.4 数形结合解决几何问题

几何问题是初中数学的重要部分之一,是每年中考数学重点考查的问题.通过几何问题,不仅可以考查学生对数学知识的实际掌握情况及应用情况,还能考查学生的综合能力及数学思维.在图3中,已知正方形和另一直角三角形边长的三边长应各应分别设为3cm、4cm、5cm.若是要我们分别都是以上所述三条边中各一条为直径来分别去计算这样一幅的半圆形,那么该形图形中的阴影部分的投影总阴影面积是多少平方厘米呢?

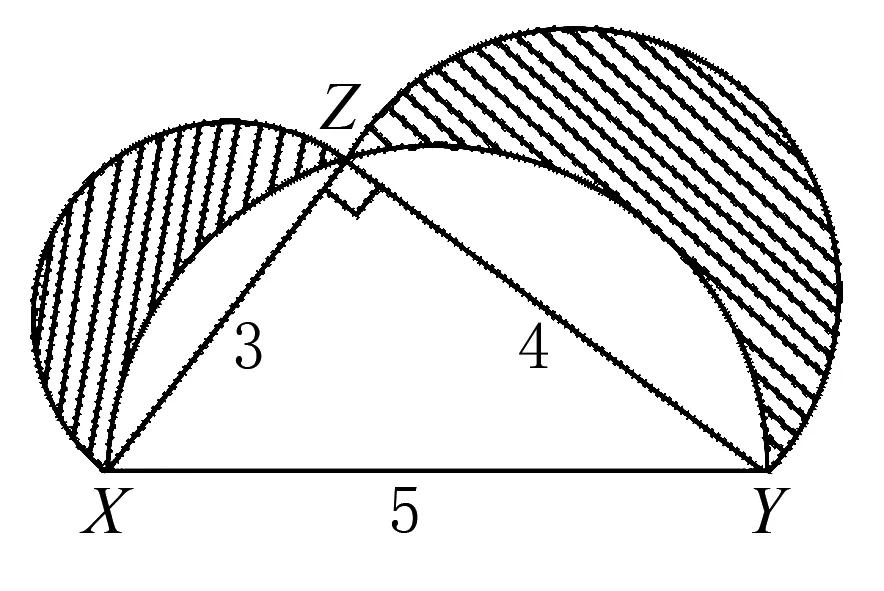
图3

通过对题干的分析可以看到，该题目的图形由三个直径分别是5cm、4cm和3cm的半圆和一个三条边长为5cm、4cm和3cm的直角三角形组成，要计算出阴影面积，就要计算出直径为3cm和4cm的两个半圆总面积，再减去它们各自的弧形面积.怎样计算这两个弧形面积的总和呢？是用直径为5cm的半圆面积减去直角三角形面积得出的.所以要想正确解答这道题，首先要计算出直径为5cm的半圆面积，然后减去直角三角形的面积，从而得到两个弧形面积的总数.随后将计算出直径为3cm与直径为4cm的半圆面积进行相加，然后减去两个弧形的总面积即可得到图中阴影部分的面积.通过这个例子，可以发现在几何问题的解答思路中数形结合思维逻辑的重要性，能够让学生快速审题，并得出问题的正确答案.

综上所述，数学结合思想对于初中数学学习与解题具有重要作用.数形结合思维逻辑可以让学生对数字与图形之间的关系产生更加深刻的理解，降低解题难度.教师要教会学生在数学解题的过程中将数形结合的思维逻辑运用起来，实现提高数学成绩的目标.