培养理性思维，提高关键能力

梁付元

摘 要：在人类社会进步与发展的历程中，特别是当今信息高度发达、技术高速发展的阶段，作为基础学科的数学，在一定程度上影响并决定着一个国家的综合实力.而渗透其中的理性思维是脉络与灵魂.其依托高考这一选拔人才的平台，借助中学数学教学，全面培养理性思维，有效提高关键能力，引领与指导高中数学教学与学习，以及人才的长远发展目标.

关键词：理性思维；关键能力；基础知识；基本技能；数学思想；思维过程

数学作为一门基础学科，也是一门思维的科学，其是培养学生的理性思维的重要土壤与关键载体之一.数学教育与数学教学的一个重要目标就是帮助学生构建、形成并发展学科思维，而其中理性思维是数学学科思维的一个综合体现.

1 夯实基础知识，完善知识结构

数学理性思维与关键能力不是独立于数学基础知识、基本技能、思想方法、数学经验之外的神秘概念，它们综合体现了对数学基础知识内在联系的理解、对数学基本技能方法的掌握、对数学思想方法的感悟、对数学思维活动经验的积累、对数学理性精神的体验等.

而“四基”（数学基础知识、基本技能、基本思想、基本活动经验）依托于数学基础知识以及由其反映出来的数学思想方法，夯实数学基础知识，掌握数学概念本质，全面完善数学知识体系与结构，是学好数学的必要条件，也是全面发展理性思维和取得理想成绩的捷径.

例1 （2022年高考数学新高考Ⅰ卷·14）写出与圆x²+y²=1和（x-3）²+（y-4）²=16都相切的一条直线的方程_________.

解析：（速解处理1）两圆外切，所以两圆相减，即得3x+4y-5=0；

（速解处理2）数形结合，直观分析，即得x=-1.

点评：以两圆位置关系为试题背景考查逻辑推理、运算求解与直观想象能力，强调数学理性思维、指向数学学科核心素养.圆的几何性质要深刻理解、灵活运用.同时还要融会贯通地理解“切线”的概念.注意用运动变化的观点以及极端化原理思考问题.

所以，数学理性思维与数学关键能力的源头是“四基”，离开了“四基”，它们就是无源之水、无本之木；没有数学理性思维的“四基”，就会失去目标与灵魂，就失去了核心价值.而“四基”的奠定又必须要求全面夯实数学基础知识，完善数学基础知识体系与整体结构.

因而，高考复习与教学必须回归数学课本，从教材体系中去全面梳理数学基础知识、基本思想方法等，并在此基础上构建全部的数学网络体系，形成一个完整的知识架构，方便由此整合知识、完善思想、优化技巧、提升效益.

2 强化基本技能，确保落实规范

数学的基本技巧主要包括以下一些基本技能：数学阅读技能——基于数学概念解读本质，在数学解题中要强调回到概念中去；数学作图技能——基于数学任务达到示意，在数学解题中要强调构建直观模型；数学推理技能——基于合情、演绎推理有理有据，在数学解题中要强调推理是命根子；数学运算技能——基于依据数学法则目标导航，在数学解题中要强调运算是“童子功”；数学表达技能——基于数学语言规范清晰简捷，在数学解题中要强调数学语言准确.

例2 （2022年高考数学新高考Ⅱ卷·7）已知正三棱台的高为1，上、下底面边长分别为33和43，其顶点都在同一球面上，则该球的表面积为（）.

A. 100π

B. 128π

C. 144π

D. 192π

综上，该球的表面积为100π，故选择答案：A.

点评：在具体求解过程中，很好地展示了数学作图技能，还要根据不同的场景进行分类处理；数学运算技能也能得以全面应用.综合解题过程中，多层面的数学技能往往都在解题过程中的不同阶段得以很好的发挥与应用，只有充分综合与利用这些数学技能，才能更好地处理与解决问题.

数学的基本技能要一以贯之地落到实处，深入到数学解题的“最前沿”，同时解题操作要规范、有序，数学运用要快速、准确.

3 感悟数学思想，培养理性思维

高考数学试卷对数学思想方法的考查融于数学基础知识的各种形式的考查之中，从而有效检测其对数学基础知识与思想方法等方面掌握的熟练程度.高考可以在选择题、填空题或解答题等不同题型中，进行数学思想方法与数学基础知识的全面考查，覆盖面更广，形式更灵活多变.

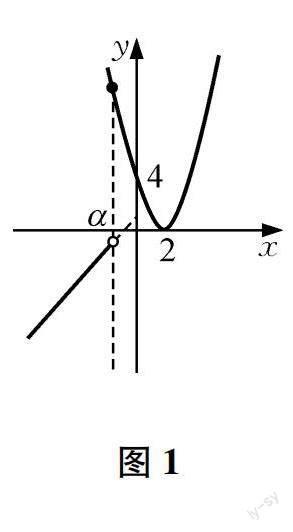
解析：当a＜0时，函数f（x）的图象如图1所示，不满足题意；

当a=0时，函数f（x）的图象如图2所示，满足题意；

当0＜a＜2时，函数f（x）的图象如图3所示，要使得函数有最小值，需满足-a²+1≥0，解得0＜a≤1；

当a=2时，函数f（x）的图象如图4所示，不满足题意；

当a＞2时，函数f（x）的图象如图5所示，要使得函数f（x）有最小值，需（a-2）²≤-a²+1，无解，故不满足题意；

综上分析，a的取值范围是［0，1］，故a的最大值为1；

故填答案：0（答案不唯一，只要在［0，1］内取值即可）；1.

点评：在实际解题过程中，借助函数自身的内涵与本质，可以回归其“数”的性质，也可以转化为“形”的结构，特别注重数形结合，这个过程中既要充分发挥“形”的直观性，又要注重“数”的严谨性，保证问题的本质属性，从而数形结合，达到繁中求简、以简驭繁是理性思维的内涵之一.

在具体数学解题过程中，要充分借助相关的数学知识体系以及技巧方法：利用严谨的方法进行逻辑推理与数学运算；利用函数或方程进行函数与方程思想应用；利用以“形”助“数”或以“数”论“形”进行数形结合思想应用；利用化整为零或聚零为整进行分类与融合思想应用；利用化繁为简、化生为熟等进行化归转化思想应用；以及特殊与一般思想、统计与概率思想的应用等，唯有如此才能培养理性思维，提高关键能力，进而提升数学学科核心素养，达到数学育人（立德树人）的目的.

4 重视思维过程，积累解题经验

某些解题技巧也许是可以传授的，但真正的解题智慧是难于口口相传的，它需要个体的亲身体会与深切感悟.“没有过程=没有思想”，只有经历概念的抽象过程、解题方法的获得过程，方能参悟到蕴含其中的思想方法，所以要给学生充分的时间进行“感悟”，切忌在匆忙中“赶误”.在此解题实践与思维过程中，通过感悟，不断积累解题经验，抽象解题智慧与解题技巧.

点评：对于以上三角函数问题，关键是挖掘题目内涵，综合三角函数的基础知识，思维角度多样，方法各异.具体解决问题中，抓住三角函数的本质，可以从定义、三角函数、平面向量、解析几何、构造对偶式及不等式等思维视角切入，结合不同的思维过程与对应的技巧方法等，实现问题的理性思维与巧思妙解.

5 總结

新高考命题越来越基础，越来越灵活，给了学生充分的时间“感悟”解题方法的来龙去脉，可以有效克服“机械刷题”的影响，这也为高中数学教学与学习指明方向，引领我们将数学应试能力的训练转向核心素养的培养，以及数学理性思维与关键能力的培育与提升等.

其实，理性思维是数学学科核心素养的一个灵魂，高考数学试卷将关键能力与理性思维、数学应用、数学探究、数学文化等数学学科素养聚焦于数学理性思维的主线之上，突出考查理性思维与关键能力.

参考文献：

［1］ 杨志芳.突出关键能力，凸呈理性思维［J］.中学数学，2021（2）：55-56.

［2］ 中华人民共和国教育部.普通高中数学课程标准（2017年版）［S］.北京：人民教育出版社，2017.