基于深度学习的概念课教学

王昭丽

摘 要：本文借助《对数函数的概念、图象和性质》这一高中数学概念课的教学实践与应用，结合深度学习的基本效益、课堂实践以及教学启示等方面，合理类比展开，阐述深度学习下概念课的基本教学实践与尝试，合理创新并应用于教学实践.

关键词：对数函数；概念；教学

基于机器学习的一种常见基本方式——深度学习，成为当今人工智能与AI技术深入发展的基础，这对学生在课堂学习与课后学习也是非常有借鉴与帮助作用的.特别是在课堂教学与学习实践中，合理联系教学课题与教学实践，利用恰当的深度学习，对数学知识与课题的联系与拓展，更深层次的理解与应用等方面有着非常重要的作用，成为新教材、新课程、新高考的“三新”背景下课堂教学的一种基本常态.

1 深度学习的基本思维

1.1 数学概念的深层理解

基于数学概念的教学与学习，借助深度学习，可以更好地挖掘不同概念之间的联系，以及相应概念的内涵与本质，联系相应概念的外延与应用，合理构建知识网络体系，形成不同数学概念之间的联系与转化.由一个概念联系到多个概念，形成有效的知识模块，合理构建更加完善的知识网络结构.

1.2 数学思维的深层拓展

从数学的基本思维入手，以课堂教学实践，通过深度学习，可以更加有效地拓展数学思维的深层理解与应用，特别是类比思维、构造思维、创新思维等，这也是深度学习所体现出来的重要优点与创新点.深度学习可以使数学思维与思想方法得到基本的提升与拓展.

1.3 数学应用的深层创新

深度学习可以让学生更深层次地学习相关的概念以及与概念相关的综合应用问题，对数学应用与数学创新都能起到更加直接的作用.由此，基于深度学习构建更多数学基础知识与基本应用之间的联系与转化，以及知识间的交汇融合等，对于数学应用与创新应用等更加得以突出与提升.

2 深度学习的课堂实践

2.1 导学聚焦

在实际高中数学概念课的课堂教学与学习时，基于相应课堂的学习目标，以及基本考点，针对对应的数学核心素养等，可以给课堂定基调，特别是数学课堂教学与学习，目的性更加明确，深度学习更加合理有效，从而紧紧围绕相应的教学与学习目标来达到目的.

2.2 问题导学

预习教材《数学》（必修第一册，人民教育出版社2019年版）第四章“指数函数与对数函数、方程和不等式”中的第四节“4.4对数函数”下的前两个小节，并思考下列相关问题：

（1）指数函数的概念是什么？它的解析式具有怎样的特点？类比拓展，对数函数的概念是什么？它的解析式具有怎样的特点？

（2）指数函数的图象是什么形状的？类比拓展，对数函数的图象是什么形状的？你能画出以下两个特殊对数函数y=log₂x与y=log_?x的图象吗？

（3）借助指数函数的图象可以观察得到相应的指数函数的基本性质，那么通过对数函数的图象，你能观察到对数函数的哪些基本性质呢？

只有真正带着问题去自主学习与自主探究，才能充分调动学生自身的积极能动性与主观性，这对课堂教学直接起到决定性的作用.特别是基于合理的问题，使得学生“跳一跳就够得着”，合理带着问题去自主学习与自主探究，借助深度学习，从而提升课堂教学质量与深度学习效益.

2.3 新知探究

2.3.1 对数函数的概念

（课本P130）一般地，函数y=log_ax（a＞0，且a≠1）叫作对数函数，其中x是自变量，函数的定义域是（0，+∞）.

2.3.2 對数函数的图象和性质

规律方法：（1）明确解决与对数函数有关的函数定义域问题时的基本原则与要求：对数的真数大于0，底数大于0且不为1.还要进一步结合函数的类型，结合分式中的分母不能为0，根式中根指数为偶数时被开方数非负等相关的应用场景加以综合与应用.

（2）求函数定义域的步骤：① 列出使函数有意义的不等式（组）；② 化简并解出自变量的取值范围；③ 确定函数的定义域.

2.4.3 对数函数的图象问题

图象的辨析判断

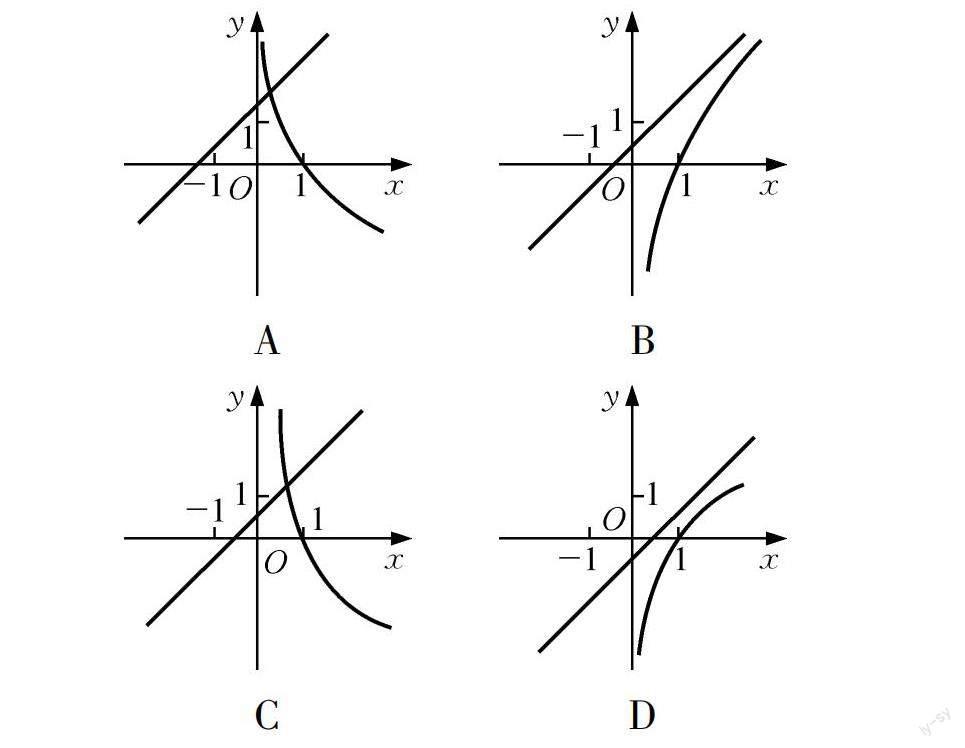
【例3】 已知a＞0，且a≠1，则函数y=x+a与y=log_ax的图象只可能是（）.

解析：当a＞1时，函数y=log_ax为增函数，且直线y=x+a与y轴的交点的纵坐标大于1；当0＜a＜1时，函数y=log_ax为减函数，且直线y=x+a与y轴的交点的纵坐标在0到1之间，只有选项C符合，故选择C.

3 深度学习的教学启示

3.1 立足基础，深度融合

基于数学概念课教学中的深度学习，立足数学的基本概念以及对应的数学基础知识，从概念的本质入手，合理加以多层面、多视角的深度学习，更加体系化、系统化地认识与理解概念的实质.

基于此，通过深度学习，从基本概念入手来强化、巩固数学基础，有效提升学习的维度与深度，从而对概念与应用等进行更加有效地深度融合，形成一个更加完善的知识体系.

3.2 把握实质，提升能力

基于数学概念课教学中的深度学习，可以更好地把握概念的实质，从而拓展与之相关的联系与应用，更加注重数学学科中的基本概念、基础知识的内核与精髓.

学生通过深度学习，可以将孤立的、碎片化的概念以及对应的知识串点成线、织网铺面，从而构建更加完整的数学知识体系，进行合理的创新与应用，夯实学生的“四基”，培养学生的创新意识与应用，培养学生的“四能”，培育理性思维，促进学生高阶思维、核心素养的发展.

参考文献：

［1］ 中华人民共和国教育部.普通高中数学课程标准（2017年版）［M］.北京：人民教育出版社，2017.