太阳同步回归轨道的轨道面外运动及在轨数据分析
杨盛庆,王文妍,杜耀珂,完 备,王嘉轶,穆少阳
(1.上海航天控制技术研究所,上海 201109;2.上海市空间智能控制技术重点实验室,上海 201109)
0 引言
太阳同步轨道由于其良好的光照条件,是对地观测卫星的一类重要轨道。近地太阳同步轨道一般为近极轨道,对地观测的纬度覆盖性能也较好。通过合理设计半长轴和轨道倾角组合,能够得到一组太阳同步回归轨道。为了使轨迹重访的轨道高度一致性较好,一般还会针对偏心率和近地点幅角进行设计,使得偏心率矢量周期运动的振幅较小,此即为冻结轨道[1]。
太阳同步回归轨道的保持,需要对轨道面内运动和轨道面外运动进行补偿控制,以实现地面轨迹的重访。轨道面内的运动主要由于大气阻力作用导致轨道衰减,轨道角速度的变化导致真实在轨的轨道相位相对于标称的轨道相位产生漂移,在地球自转的联合作用下使得地面轨迹产生漂移。轨道面外的运动,包括由于日月三体摄动引起的轨道倾角长期变化和复合多周期变化,由于轨道倾角和半长轴的差异使得地球非球形引力场下(主要是J2 项摄动)降交点地方时产生长期的漂移。文献[2]分析了倾角的长期变化,主要针对某个降交点地方时的太阳同步轨道的倾角年漂移量及其解析解,给出了半长轴的偏置控制策略以保持轨道的降交点地方时。文献[3]研究了通过近圆太阳同步轨道卫星倾角修正控制使卫星降交点地方时反向漂移的方法。上述方法从力学层面阐述了太阳同步回归轨道的轨道面外运动特征与控制方法。未来航天器的发展将朝着智能自主的方向发展[4-5],高性能的处理系统和复杂的导航制导算法将使得星上自主的轨道面外控制成为可能。国外在合成孔径雷达(Synthetic Aperture Radar,SAR)载荷成像卫星领域开展精确回归/严格回归轨道的技术研究和型号研制,目前在轨应用的主要有欧洲航天局(European Space Agency,ESA)的Sentinel 卫星和日本宇宙航空研究开发机构(JAXA)的ALSO 卫星[6]。在国内,上海航天技术研究院着力发展合成孔径雷达遥感技术[7],包括编队InSAR 干涉成像和空间轨迹重访干涉成像[8]。上海航天技术研究院研制了国内首个具有严格回归轨道控制任务的陆探一号卫星,已于2022 年初发射入轨,进入轨道高度约600 km 的太阳同步回归冻结轨道,具备自主管道导航[9]和管道保持能力[10]。管道导航与保持的参考轨道是一组考虑高阶地球非球形引力场作用的地固系位置、速度参数。为了使参考轨道能够重复使用,未考虑非保守力摄动和历元相关的日月三体摄动[9-10]。文献[6]中指出,轨道倾角的半月周期运动是卫星相对参考轨道运动突破管道边界的一项重要因素。陆探一号需要实现围绕空间轨迹的百米量级管径保持,轨道面外的运动不容忽视。基于轨道倾角的半月周期运动特性设计合理的管径并构造对应的控制策略,能够有效减少控制的总能耗需求。文献[11-12]分析了地球非球形引力场不同阶次影响下的降交点地方时漂移估计方法,文献[13]进一步给出了降交点地方时保持的偏置控制方法。但是,上述方法未考虑半月周期的倾角周期运动,该项运动主要由月球的天体运动造成[6]。文献[14-16]具体给出了日月三体摄动影响下,轨道倾角周期运动的解析解形式。
精确回归轨道一般选取太阳同步回归冻结轨道,是地球观测卫星的一类重要轨道。太阳同步轨道能源环境较好,同时回归冻结轨道特征实现了空间轨迹的高精度重访。太阳同步轨道的空间摄动环境较稳定,表现为卫星轨道面与太阳和月球的空间相对位置关系较确定,三体摄动长期效应、长周期效应、短周期效应明显且稳定。特别地,陆探一号的轨道属于太阳同步轨道中的晨昏轨道,其由三体摄动引起的长期效应基本可以忽略。这为分析三体摄动的周期效应提供了较好的空间环境基础。本文基于陆探一号的在轨遥测数据,分析了轨道面外运动的特性。针对轨道倾角的半月周期运动和降交点地方时的漂移进行了解析,同时,针对陆探一号自主管道导航与管道保持控制任务,分析了虚拟编队构形参数与轨道运动的面外参数(轨道倾角偏差、降交点地方时偏差)的相关性。
1 轨道动力学原理
1.1 轨道面外参数与坐标系统
已知惯性系位置r、速度v,轨道角动量h定义[17]如下:.
由此可以定义轨道倾角i和升交点赤经Ω如下[18-20]:
对在轨数据进行分析,最原始的轨道测量信息是时间历元和地球固联WGS84 坐标系下rWGS84、vWGS84。国际天球参考系(International Celestial Reference System,ICRS)与国际地球参考系统(International Terrestrial Reference System,ITRS)之间的坐标系转换涉及岁差PR、章动NR、地球自转ER和极移EP的修正。国际天文学联合会(International Astronomical Union,IAU,)定期发布坐标系转换标准。较新的标准有IAU2000、IAU2006等。轨道积分常用的J2000.0 历元惯性坐标系下rI、vI,属于平春分点平赤道参考坐标系。WGS84坐标系到J2000.0 历元惯性坐标系的转换公式如下:
式中:rWGS84为WGS84 坐标系位置。
分析轨道倾角的运动,应当在真春分点真赤道参考坐标系[16]。WGS84 坐标系到真春分点真赤道参考坐标系的转换公式如下:
使用真春分点真赤道参考坐标系下位置、速度可以计算得到轨道参数的瞬根。
1.2 非球形引力场及短周期项[18]
一阶长周期项Δ1il、Δ1Ωl,其解析式如下:
根据上述一阶短周期项和一阶长周期项,可以由轨道参数的瞬根计算得到平根。
1.3 天体运动[15]
太阳天体运动的参数主要有偏心率es、黄赤交角ε、太阳的几何平黄经Ls、太阳平近点角Ms:
式中:JC 为自历元J2000.0 起算的儒略世纪数。太阳的近地点平黄经ωs=Ls-Ms。
月球天体运动的参数主要有轨道偏心率em=0.054 879 905,轨道倾角im=5.129 835 017°,绕地球公转周期Tm=27.321 662d(恒星月)。白道的升交点黄经Ωm、月球的平黄经Lm、近地点平黄经ωm分别为
1.4 摄动项及其微分形式
对于近地太阳同步轨道,日月三体摄动是轨道倾角长期运动和周期运动的主要因素。由于太阳同步特性,使得不同降交点地方时的轨道面和太阳矢量的夹角状态稳定,因此轨道倾角的年累积漂移量与轨道降交点地方时相关,如图1 所示。太阳引力摄动作用下轨道倾角的微分形式[14]如下:

图1 不同降交点地方时轨道的倾角年累积漂移量Fig.1 Cumulative annual drifts of the orbital inclination at different local time of descending node
月球引力摄动作用下轨道倾角的微分形式[14]如下:
2 轨道倾角的周期运动
2.1 轨道倾角的解析解与周期运动特征[6]
式中:ns为太阳轨道运动的平均角速度;n为航天器轨道运动的平均角速度;Csk、αsk为周期运动的相关参数。
式中:nm为月球轨道运动的平均角速度;κm、Cmk0、Cm2-2、αm2-2为周期运动的相关参数;半月周期运动主要由引起,其解析式可由式(13)和式(14)代入式(12)相关项中计算得到,
2.2 虚拟编队构形参数的相关性
根据编队构形参数的定义[21-22],使用卫星与参考轨道的相对轨道拟平根数定义虚拟编队的轨道面外构形参数如下:
式中:aref为参考轨道的半长轴;iref为参考轨道的轨道倾角。
虚拟编队构形参数的漂移量可以表示为轨道面外参数的漂移量,公式如下:
式中:偏导数项满足式(17);下标ref 表示参考轨道。
从式(18)可以观察到,对于虚拟编队构形参数s、φ,轨道面外参数Δi、ΔΩ产生的影响与其当前比值相关,且φ的变化与Δi的变化极性相反。
2.3 参考轨道的轨道面外运动特征
对自主管道导航使用的参考轨道进行分析,确定了其轨道面外的运动特征。基准目标轨道为地面优化设计的严格回归轨道,太阳同步特性好(降交点地方时变化小),如图2(a)和图2(b)所示。设计严格回归轨道时未考虑日月三体摄动,因此轨道倾角无长期累积项和半月周期运动。回归周期为8 d,从图2(a)和2(b)中可以观察到无半月周期的特征。
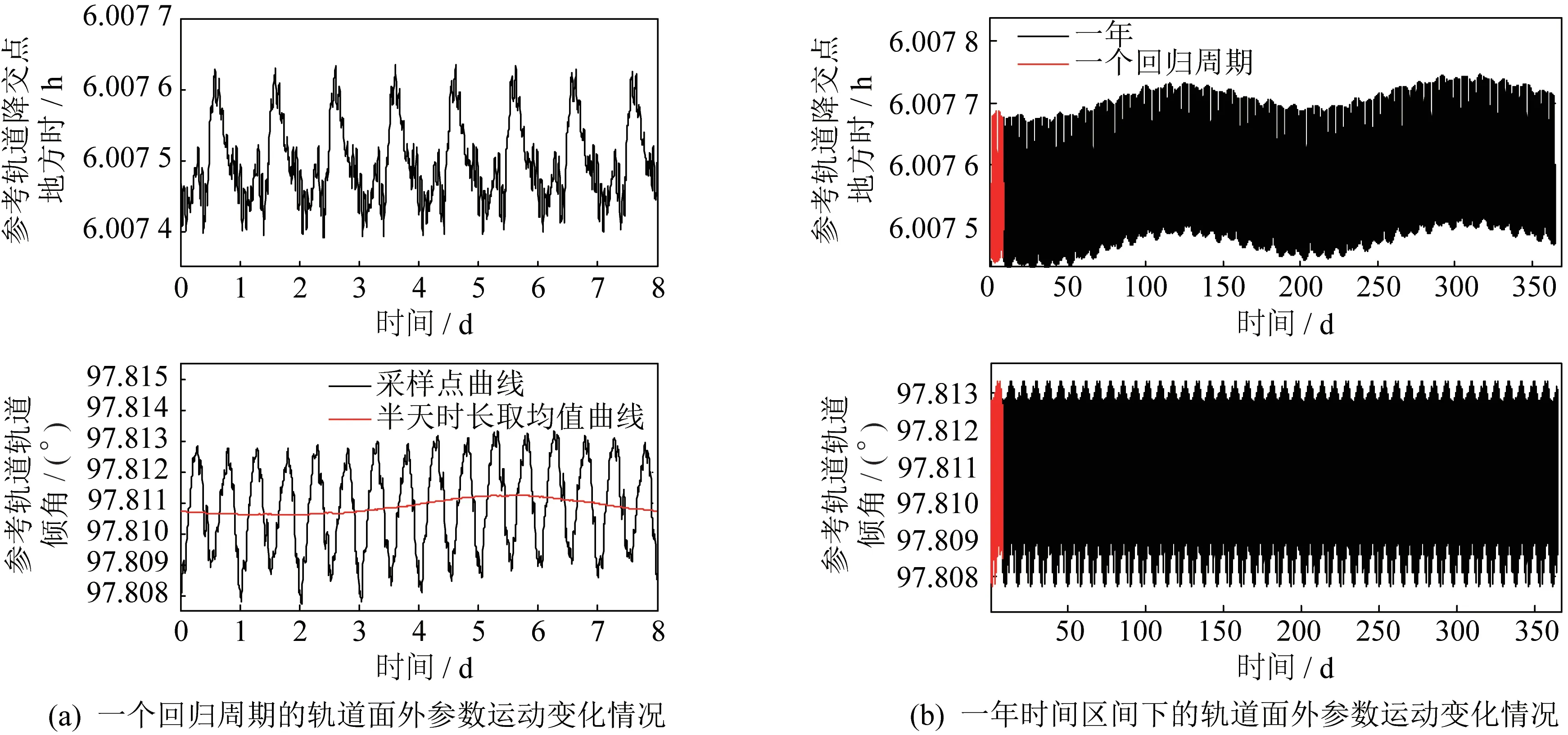
图2 参考轨道的轨道面外参数运动变化情况Fig.2 Out-of-plane orbital parameter motion of the reference orbit
3 轨道倾角的运动特性
3.1 轨道倾角的周期运动特征
对陆探一号卫星及其前序型号卫星的在轨遥测数据进行分析处理,如图3(a)和图3(b)所示平春分点平赤道坐标系下轨道倾角的运动变化包含岁差、章动的修正效应,轨道倾角的年周期运动幅值较大。在真春分点真赤道坐标系下,轨道倾角能够真实反映日月三体摄动导致的年周期和半月周期运动特征。

图3 在轨的轨道倾角运动变化情况Fig.3 In-orbit motion of the orbital inclination
3.2 降交点地方时确定
轨道的降交点地方时可以根据相同历元下升交点赤经和太阳几何平黄经计算确定,陆探一号卫星入轨后2 个月时间内的降交点地方时运动变化情况如图4(a)所示,前序型号在轨两年时间内降交点地方时变化情况如图4(b)所示。通过比对可以观察到,陆探一号卫星的严格回归轨道保持稳定,使得轨道的降交点地方时变化较小。

图4 在轨的降交点地方时运动变化情况Fig.4 In-orbit motion at the local time of descending node
3.3 倾角的半月周期运动与数据驱动分解
针对轨道倾角存在的半月周期运动,对陆探一号卫星及其前序型号卫星的在轨遥测数据进行数据驱动的周期运动分解。得到半月周期的运动规律如图5(a)下分图和图5(b)下分图所示,其周期运动的幅值约1×10-3°。
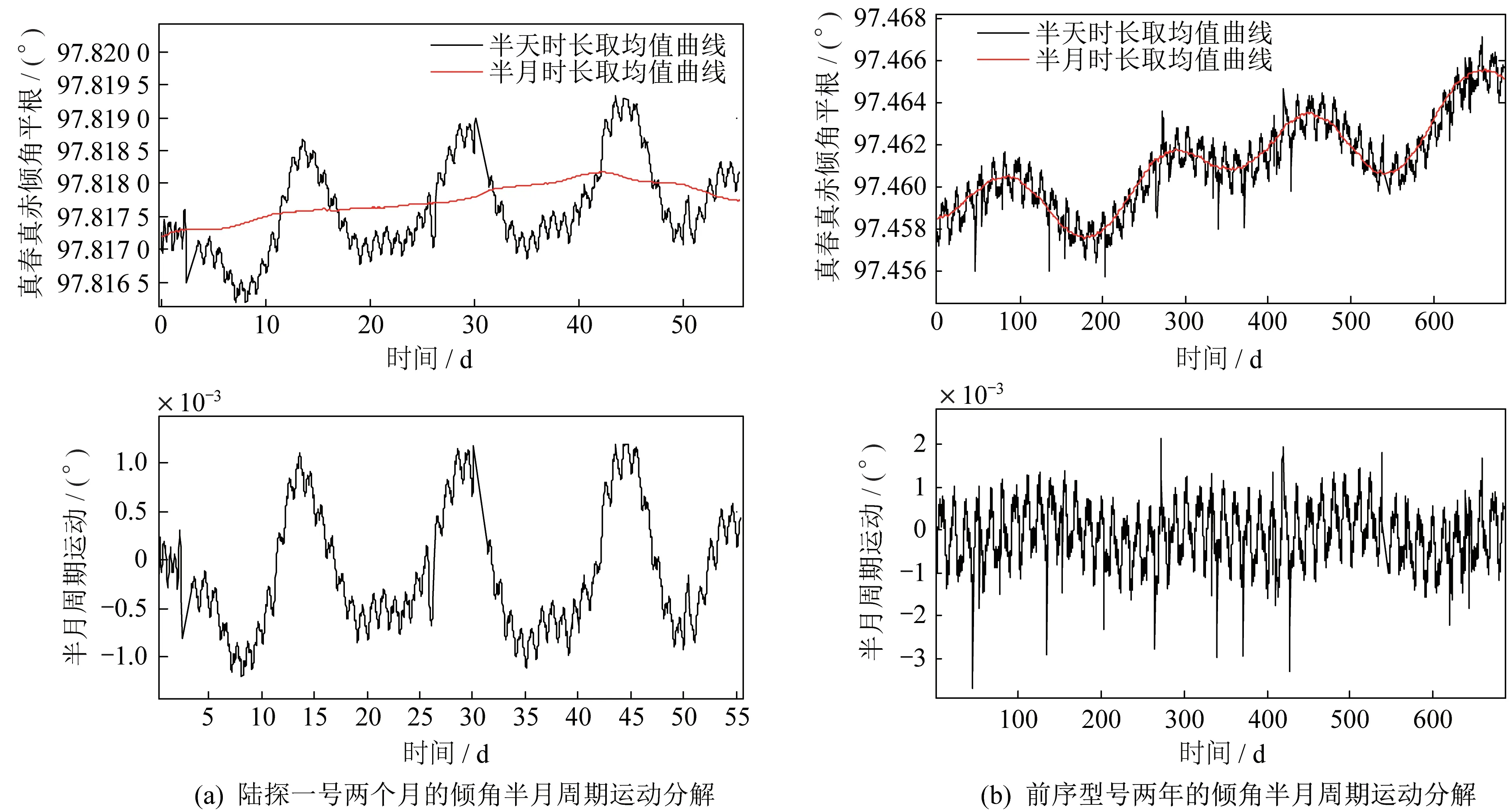
图5 在轨数据的倾角半月周期运动分解Fig.5 Half month period motion identification of the orbital inclination based on the in-orbit data
使用式(12)~式(14)计算轨道倾角半月周期运动的解析解,并与数值分析数据进行比对,进一步验证了倾角的半月周期运动特性,轨道倾角的半月周期运动与解析解的比对情况如图6 所示。数值解的计算基于地面获取的批量GNSS 测量数据,窗口平均的分析方法所需的数据存储量和计算量较大。解析解仅由时间历元和卫星轨道根数确定,无需存储大量数据且计算量小。能够快速高效地得到轨道倾角的变化状态,可以作为轨道面外运动轨迹优化的基础。解析解基于日月势场函数表述的摄动模型,卫星在轨除受到三体摄动影响外,还受固体潮、液体潮摄动(主要源于三体摄动)的叠加影响。目前,解析解和数值解确定的周期性波动,其相位吻合,峰值残差约4×10-4°。利用解析解进行自主轨道面外控制规划时,若残差是一个稳定状态,可以进行标定和补偿。

图6 轨道倾角的半月周期运动与解析解的比对情况Fig.6 Comparison of the in-orbit data and analytical solution for the half-month period motion of the orbital inclination
3.4 虚拟编队构形与轨道面外运动的相关性验证
根据陆探一号在轨数据确定卫星相对参考轨道的轨道面外参数Δi、ΔΩ,根据式(15)计算虚拟编队构形参数如图7 所示。当前,根据式(18)可知,s的变化主要响应ΔΩ的变化,φ的变化主要响应Δi的变化且极性相反。
4 结束语
本文基于陆探一号的在轨遥测数据,分析了入轨后2 个月内轨道倾角和降交点地方时的运动变化规律。基于数据驱动方法对日月三体摄动导致的轨道倾角的周期运动进行了辨识与分解,对于主要由月球天体运动导致的倾角半月周期运动,在轨数据与经典的解析解基本一致,解析解可以作为倾角半月周期运动的预报依据。本文所得的轨道面外运动特性能够印证自主管道导航计算的虚拟编队构形参数的变化情况,相关结论能够有效支撑自主管道导航的应用拓展和自主管道保持的管径优化设计。

