一种基于在轨深度学习的压缩率确定方法

张舒啸，施 琦，陈 雯，余金培

（1.中国科学院 微小卫星创新研究院，上海 201203；2.上海科技大学 信息科学与技术学院，上海 201210；3.中国科学院大学，北京 100049）

0 引言

如何对遥感图像中的重要目标进行精确的识别分类，是卫星遥感领域的一个难点和重要研究方向。近年来，对遥感图像目标检测的技术有不少发展，钮赛赛等［1］、方青云等［2］都基于YOLO 模型实现了遥感图像目标检测。但是遥感在轨图像存在数据量大，存储、下传到地面的速度受限，时间延迟大的问题。如果能及时进行在轨识别处理，可提高时效性，降低对星上存储及数据下传的压力，当然这会增加在轨识别处理的资源要求。星上硬件设备受限，计算能力不足，要做到在轨识别，需要以识别精度为代价来降低计算成本，在计算量受限的条件下进行遥感图像目标识别则更是困难。深度学习能较好地解决识别分类的问题，但是深度学习模型有大量参数，会消耗大量计算和存储资源，不利于在星上部署。模型压缩可以有效地去除冗余信息，节省存储空间，减少计算量，适合于这种资源受限的应用场景。剪枝作为模型压缩的重要手段，已被广泛运用。

对于剪枝技术的研究有很多：LUO 等［3］提出了过滤器级别的剪枝方法ThiNet；HE 等［4］提出基于软更新的软滤波器剪枝（Soft Filter Pruning，SFP）方法对网络进行剪枝；YU 等［5］提出了一种根据情况自适应修改通道数量的网络模型，将不同压缩率的网络训练到一个网络里。以上几种方法都是预定义的剪枝方法，除此之外还有一些自动剪枝的方法。HE［6］提出了一种基于深度确定性策略梯度（Deep Deterministic Policy Gradient，DDPG）的自动压缩方法。LIN 等［7］提出了ABCPruner 修剪方法，LIU 等［8］提出了一种基于元学习的修剪方法，DONG 等［9］使用可变形结构搜索和知识蒸馏的方法来搜索小型网络。

预定义剪枝方法的压缩率以及每一层的剪枝比例一般通过人工设置，缺乏选择依据。自动剪枝方法如果通过人工设置总的压缩率，同样缺乏选择依据。自动剪枝方法如果通过相应算法得到每一层的剪枝比例，压缩算法结束之前不知道总的压缩率是多少，且最终得到的总的压缩率可能不满足资源限制要求。该搜索方法无法折衷考虑准确率和运算量对实际应用场景的影响。为了根据应用需求确定压缩率，本文研究贡献如下：1）提出了一种描述压缩后计算量与准确率关系的函数模型；2）运用该模型可以根据不同应用场景需求确定合适的压缩率；3）运用该模型可以对不同的压缩方法进行比较。

1 压缩方法

本文从预定义剪枝方法中选取等比例剪枝作为代表，从自动剪枝方法中选取自动机器学习（Automated Machine Learning，AMC）算法作为代表进行实验。

1.1 等比例剪枝

MITTAL 等［10］通过实验论证了对过滤器的随机裁剪能得到基于权重裁剪模型相似的准确率。LIU 等［11］则提出了剪枝的本质是对模型的结构的调整，而不是对重要权重的保留。在此之前的压缩方法主要是手动设置模型结构，调整压缩率，如Thi-Net，或者是对每一层的结构采用相同的比例进行剪枝，如SFP。由于手动调整结构不具有一般性，本文将对每一层采用相同的比例进行剪枝，剪枝后从头开始训练，然后对剪枝效果进行评估。对神经网络的第i层进行剪枝如图1 所示。

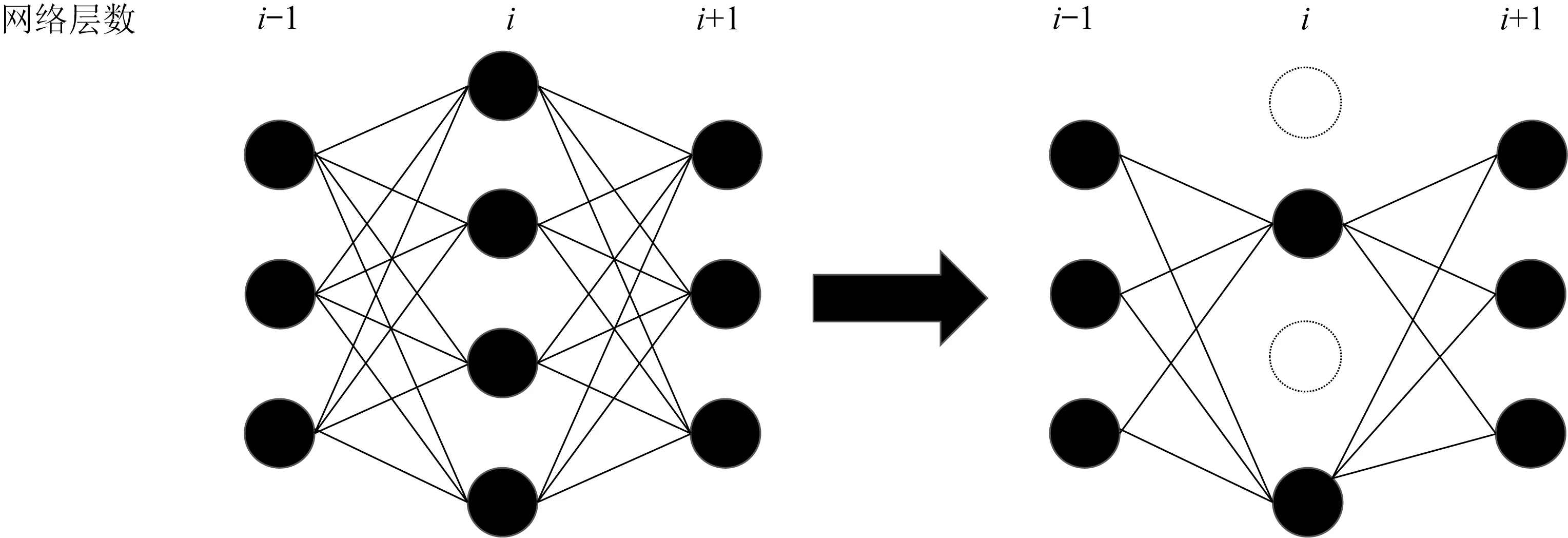
图1 对神经网络的第i 层进行剪枝Fig.1 Pruning of the ith layer of the neural network

1.2 AMC

AMC 算法［6］由HE 等提出，是一种基于强化学习的压缩方法，此压缩方法的核心是DDPG。动作空间at∈(0，1]，表示第t层的剪枝率，状态空间S为(t，n，c，h，w，stride，k，FLOPs[t]，reduced，rest，at-1)。其中：t为层数；n为输出通道数；c为输入通道数；h为输入层的高；w为输入层的宽；stride为步长；k为卷积核的大小；FLOPs[t]为第t层浮点运算次数（floating point operatens，FLOPs）；reduced 是之前层减掉的FLOPs；rest 是剩余层的FLOPs；at-1是一个（0，1］的动作空间，表示第t-1 层的剪枝率；奖励函数R=-Error 或R=-Error*log(FLOPs)，这两种奖励函数前一种是确定FLOPs，只针对准确率进行学习，后一种奖励函数要同时对两者进行学习。此方法有两个神经网络：Actor和Critic，其损失函数分别为

式 中：ri为 第i个奖励函数；si为第i个状态；ai为 第i个动作；Q为动作价值函数；b为奖励函数的均值；θ为网络参数；γ设置为1；μ(si)为状态si下的动作a。

2 计算量与准确率的函数关系

一般情况下，模型压缩后的计算量越小，即模型压缩率越大，此时准确率越低。模型压缩就是用准确率的下降换取资源需求的减少。然而不同的应用场景，对于压缩率的要求不同，对压缩后模型的准确率要求也不尽相同。为了更加清晰地展示不同情况下准确率下降与消耗资源减少的关系，以便更好地确定压缩率，用函数来拟合准确率与模型压缩之后计算量之间的关系。

由于模型的准确率和计算量之间关系的限制，需要拟合的函数需满足以下条件：1）对于任何分类任务，定义域是［0，100］，值域是［0，100］的子集，单位是%；2）函数在定义域内连续且单调递增。

选择满足上述条件的函数能在一定程度上避免过拟合。通过分析比较多种函数模型后发现分子分母为同阶多项式的函数可以很好地拟合出准确率与计算量的关系改变趋势。而深度学习模型计算量大，考虑实际需求，减少拟合函数所需要的最少数据点，可以减少总的计算量，定义函数关系如下：

式中：x为剪枝后模型所需计算量占初始模型所需计算量的百分比，即x=1-ratio，ratio 表示压缩率，即压缩的计算量占初始模型计算量的百分比；y为模型的Top1 准确率，即正确分类的目标数量占总数的百分比；p1、p2、p3、q1、q2为要拟合的参数。

3 模型参数的拟合

要用函数（3）拟合准确率与计算量的关系，需要在定义域［0，100］内采样n个点(x1，y1)，(x2，y2)，…，(xn，yn)。为了更完整地拟合整条曲线，取一个极限的点(0，y0)，其中y0的值为理论情况下的极限值，即在不通过模型计算的情况下将随机生成的结果作为模型输出结果能得到的准确率的理论值，最后最小化损失函数F为

接下来，需要针对p1、p2、p3、q1、q2计算F的偏导数；再使用梯度下降法来得到p1、p2、p3、q1、q2的值。梯度下降的参数的迭代更新公式为

式中：φ可以用p1、p2、p3、q1、q2这些参数替换；lr为学习率；为偏导数。

通过式（5）可以得到计算量与准确率的关系，并可根据准确率或者准确率与压缩率的折衷关系来确定压缩率。不同的场景对压缩率的要求各不相同，可根据实际需要求压缩率，如设定一个阈值ε，并求，或者直接根据准确率求，此时的压缩率即可满足要求。

4 仿真分析及结论

本次实验使用了CIFAR10 数据集［12］和遥感图像数据集UCMerced Land-Use［13］，其中CIFAR10 数据集有60 000 张图片，其中50 000 张为训练集，10 000 张为测试集，分为10 个类，每张图片的大小为32×32×3。UCMerced Land-Use 数据集共有21类，每个类100 张图片，每张图片的大小为256×256×3，训练时将图片裁剪为224×224×3，随机将每个类别的80 张图片作为训练集，20 张图片用作测试集。

实验内容为在CIFAR10 数据集上分别用等比例剪枝和AMC 自动剪枝方法对ResNet20、ResNet56［14］、VGG16［15］深度神经网络以不同的压缩率进行剪枝，将剪枝后的模型在数据集上进行训练和测试，并将结果中80%的数据用函数拟合不同模型下准确率与计算量的关系，剩下的20%的数据用来检验拟合数据的效果。

神经网络都采用交叉熵损失函数，等比例压缩方法采用压缩后从头训练方式，AMC 方法按照原文采用训练后微调的方式，两种方法都训练200 批次，初始学习率为0.1，并在第100、150 批次分别衰减0.1，AMC 微调100 个批次。

拟合函数采用随机梯度下降法，等比例压缩算法共有19 个数据点，其中15 个用于拟合，4 个数据点用于测试，AMC 算法共有7 个数据点，其中6 个数据点用于拟合，1 个数据点用于测试，共迭代60 000 次，初始参数为1 到100 的随机数；初始学习率为0.1，并在第500次和第59 500次迭代衰减0.1。

除了上文提到的函数模型式（3）外，还尝试使用其他模型来拟合准确率与计算量关系的曲线，如图2 所示。

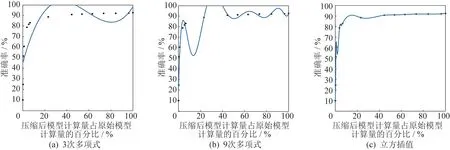
图2 其他常用模型拟合效果Fig.2 Fitting effects of other commonly used models

这些数据为用等比例剪枝的方法在ResNet20上压缩后在CIFAR10 上分类的结果。这三种方法在测试集上的均方根误差分别为13.96、19.22、4.66。这些方法的拟合效果都不够理想，而线性插值方法要得到好的结果需要的数据点过多。分子分母为更高阶的函数也可以拟合，但是更容易出现间断点，且对数据量的需求更高。因此，式（3）给出的函数可以较好满足应用需求。拟合曲线参数及拟合效果见表1。表1 第一列中的Method1 为使用等比例剪枝的方法，Method2 为使用AMC 自动剪枝算法，最后一个数字表示数据集，1 表示CIFAR10，2 表示UCMerced Land-Use 数据集，第一行的p1、p2、p3、q1、q2表示拟合参数，RMSE 是拟合的曲线在测试数据上的均方根误差，用以检测拟合曲线的拟合效果。

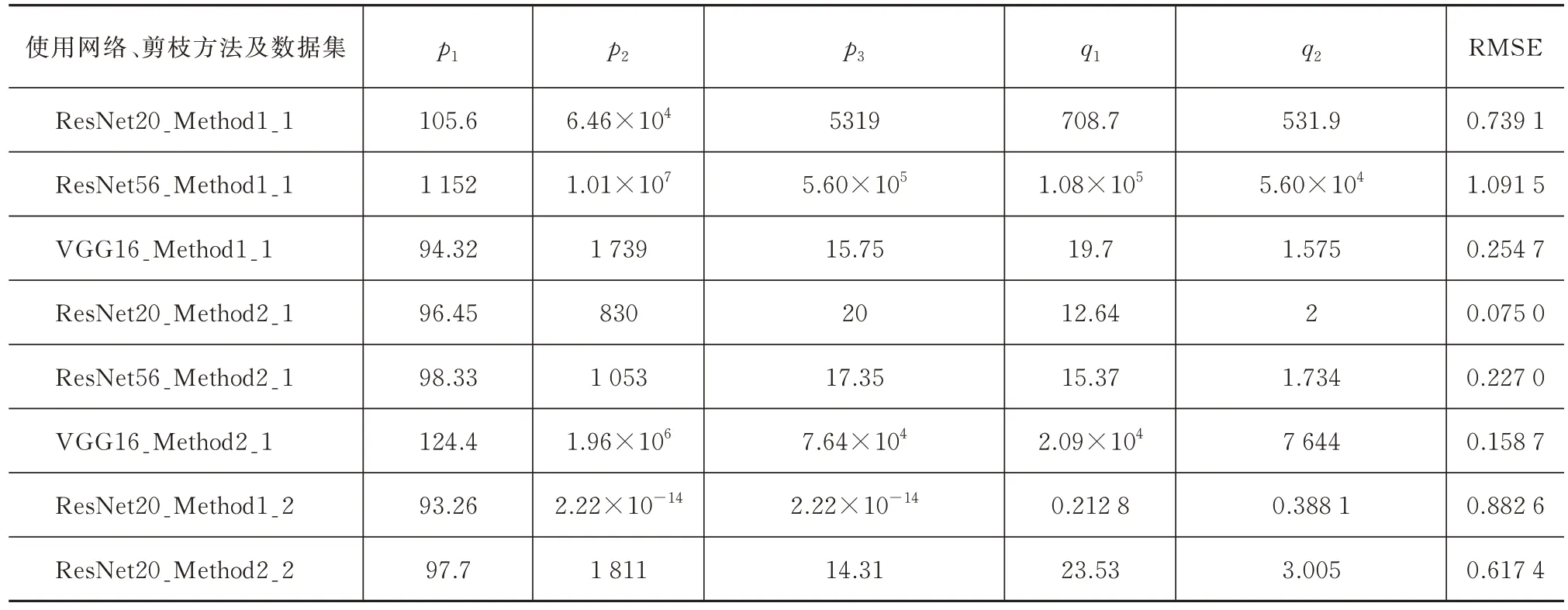
表1 拟合曲线参数及拟合效果Tab.1 Fitting curve parameters and fitting effects

不同剪枝方法在相同模型上进行压缩后的比 较图如图3 所示。

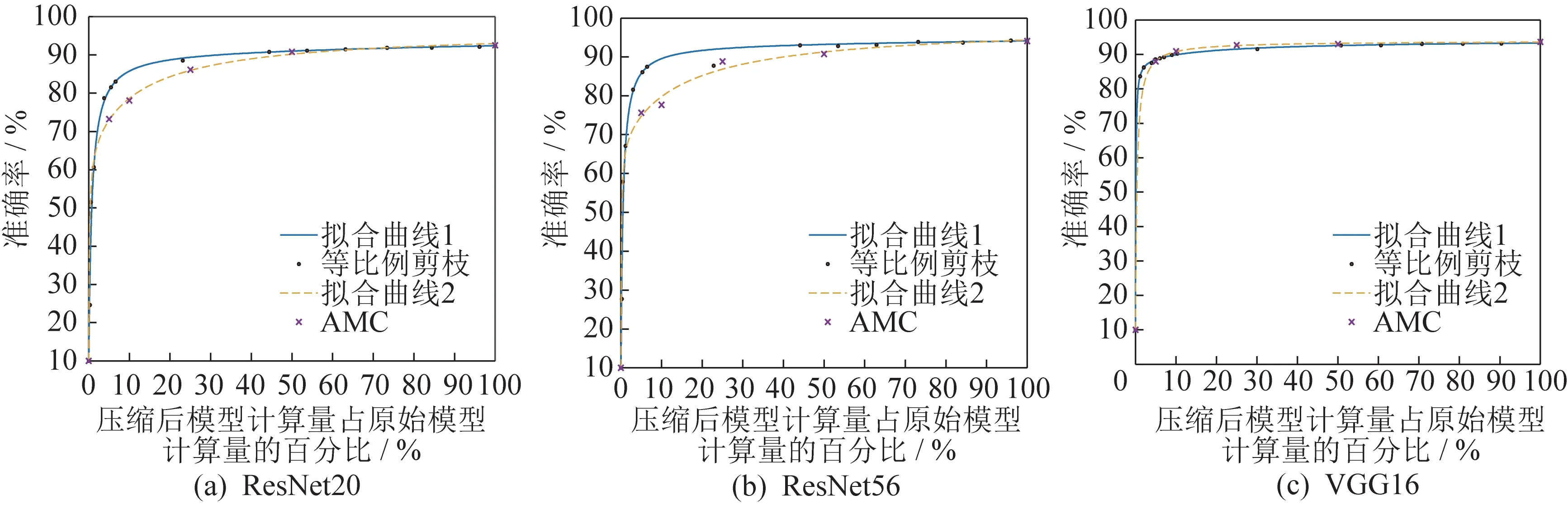
图3 不同剪枝方法在相同模型上进行压缩后的准确率比较Fig.3 Comparison of the accuracy of the same model obtained by different pruning methods after compression

图2中的3张图片分别为对ResNet20、ResNet56、VGG16 用2 种方法以不同的压缩率压缩后在CIFAR10 数据集上的准确率，其中，横坐标表示压缩后的模型的计算量占原始模型的百分比，纵坐标表示准确率。可以看到，在压缩率较低时，两种压缩方法各有优劣，在压缩率较高时等比例剪枝方法较好。2 种压缩方法压缩ResNet20 后在UCMerced Land-Use 数据集上的结果如图4 所示。

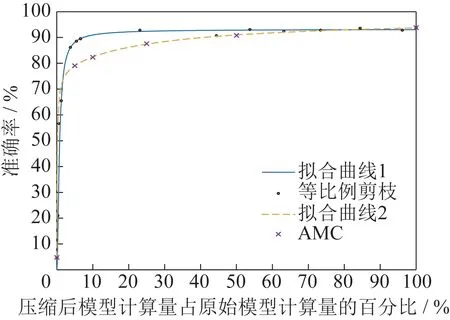
图4 两种压缩方法压缩ResNet20 后在UCMerced Land-Use 数据集上的结果Fig.4 Results of the ResNet20 model on the UCMerced Land-Use dataset obtained by the two compression methods after compression

图4 中的图片表示以同样的方法使用ResNet20在UCMerced Land-Use 数据集上的结果，可以看到数据的变化趋势与在CIFAR10 数据集上相同。

通过以上实验可以得到以下结论：

1）采用式（3）拟合的曲线与其他函数形式相比误差较小，能较好地反映变化的趋势。

2）有了以上曲线模型后，可以针对应用场景需求，根据准确率要求或者准确率与压缩率的折衷人工确定模型压缩率后进行压缩，从而可解决选择压缩率时无选择依据的问题。

3）可以根据得到的拟合曲线对不同的压缩方法性能进行比较，只要比较曲线与x=0、x=100、y=0 三条直线围成的面积大小（即曲线在定义域内的定积分）即可。从图3 可以看出，不同的压缩方法要减少相同的计算量时损失的准确率是不一样的，等比例剪枝和AMC 算法在压缩率较小时，效果不相上下，当压缩率较大时，等比例剪枝效果更好。

4）压缩方法对同一个模型压缩后在不同数据集上的表现相似，使用该方法可以在一定程度上根据一个数据集上的表现推断此压缩方法在另一个数据集上的表现。

5 结束语

本文针对卫星在轨识别使用深度学习方法时压缩率的选择问题，给出了计算量降低与准确率损失的量化关系拟合方法。该方法可给出压缩率与准确率两者之间的折衷关系，为设置压缩率提供依据，可以避免使用算法搜索得到压缩率方法存在的问题。同时，有了压缩率与准确率之间的折衷关系的曲线后，还可以对不同的压缩方法进行比较。