复杂运动下弹载雷达杂波建模方法

杨 豪，余渝生，王志城，孙永岩，刘艳阳，林 欣，黄鹏辉，邹子豪

（1.上海交通大学 电子信息与电气工程学院，上海 200240；2.上海航天技术研究院，上海 201109；3.上海卫星工程研究所，上海 201109）

0 引言

近年来，随着战场环境的快速变化和先进军事运动目标的出现，现代战场态势变得越来越复杂，高威胁动目标难以被检测和跟踪。导弹作为一种战略武器，能够有效地实现对时敏运动目标的打击，在现代战争中发挥着越来越重要的作用［1-5］。为了进一步提高导弹的攻击性能，需要精确制导技术和主动制导能力，使新一代导弹在全天候条件下展现出强大的昼夜超视距发射能力［6］。在导弹的导引头上装载雷达可以实现雷达的精准索敌与主动制导，但导弹的运动情形与飞机不同，为了精确打击目标，除平动之外，在弹道飞行过程中还具有俯冲运动［7］。此外为了保持弹体飞行稳定性，同时减少推心偏力，导弹会进行自旋，自旋会进一步引起进动与章动现象［8-9］。因此弹载雷达与机载雷达回波的特性有所区别，导致传统对平动情形下的雷达平台接收杂波的建模方法不再适用于弹载雷达。

对弹载平台的雷达接收杂波进行准确的建模和仿真，对后续分析其杂波特性、进行杂波补偿以及杂波抑制具有重要意义。但导弹的复杂运动使得分析其杂波特性十分困难。王永良等［10］在传统机载正侧视雷达的基础上考虑了不同类型雷达的杂波建模，将相控阵、多输入多输出（Multi-input Multi-output，MIMO）雷达和共形阵雷达等平台的杂波建模方法进行了统一，但其雷达平台只考虑了平动飞行，对于弹载平台而言不适用。许京伟等［11］在弹载雷达前视的基础上，考虑了导弹俯冲的运动情形，对前视俯冲的弹载雷达回波进行建模，并分析了其杂波特征，比传统的平动模型更加贴合实际，但并未考虑到导弹具有自旋、进动与章动等复杂运动的影响。孙璟潇等［12］在弹载平台前视俯冲的基础上，对导弹自旋时的回波特性进行了建模与分析，但忽略了导弹自旋引入的进动与章动影响。

针对弹载平台复杂运动情形下杂波特性不再匹配平动杂波模型的问题，本文对弹载平台具有俯冲、自旋、进动与章动的运动情形进行精确建模，结合弹载平台的运动模型，给出了多通道弹载雷达的地面杂波精确信号模型。最后通过仿真结果分析其杂波的空时特性，为杂波的补偿、抑制等处理建立理论基础。

1 平台运动模型

1.1 进动与章动

弹体除了绕自身对称轴旋转以外，其对称轴还会绕另一矢量方向进行旋转，这种运动呈现一个锥体的形状，称为锥旋，自旋加上锥旋即为进动（Precession），如图1 所示。平底锥体为导弹头，Oprecx是其对称轴，弹体绕Oprecx轴自转，OprecA方向为进动轴，进动点Oprec是OprecA与Oprecx的交点，Oprecx轴绕OprecA矢量方向旋转，角ξ称为章动角，ωs与ωp分别是自旋角速度与进动角速度。

如章动角ξ在导弹飞行过程中发生变化，即弹体在章动角所在的平面内进行较小波动时，这种现象称为章动（Nutation），如图2 所示。弹体以Oprec为中心在OprecA轴与Oprecx轴所确定的平面内进行波动，此时波动角度θnut表达式为

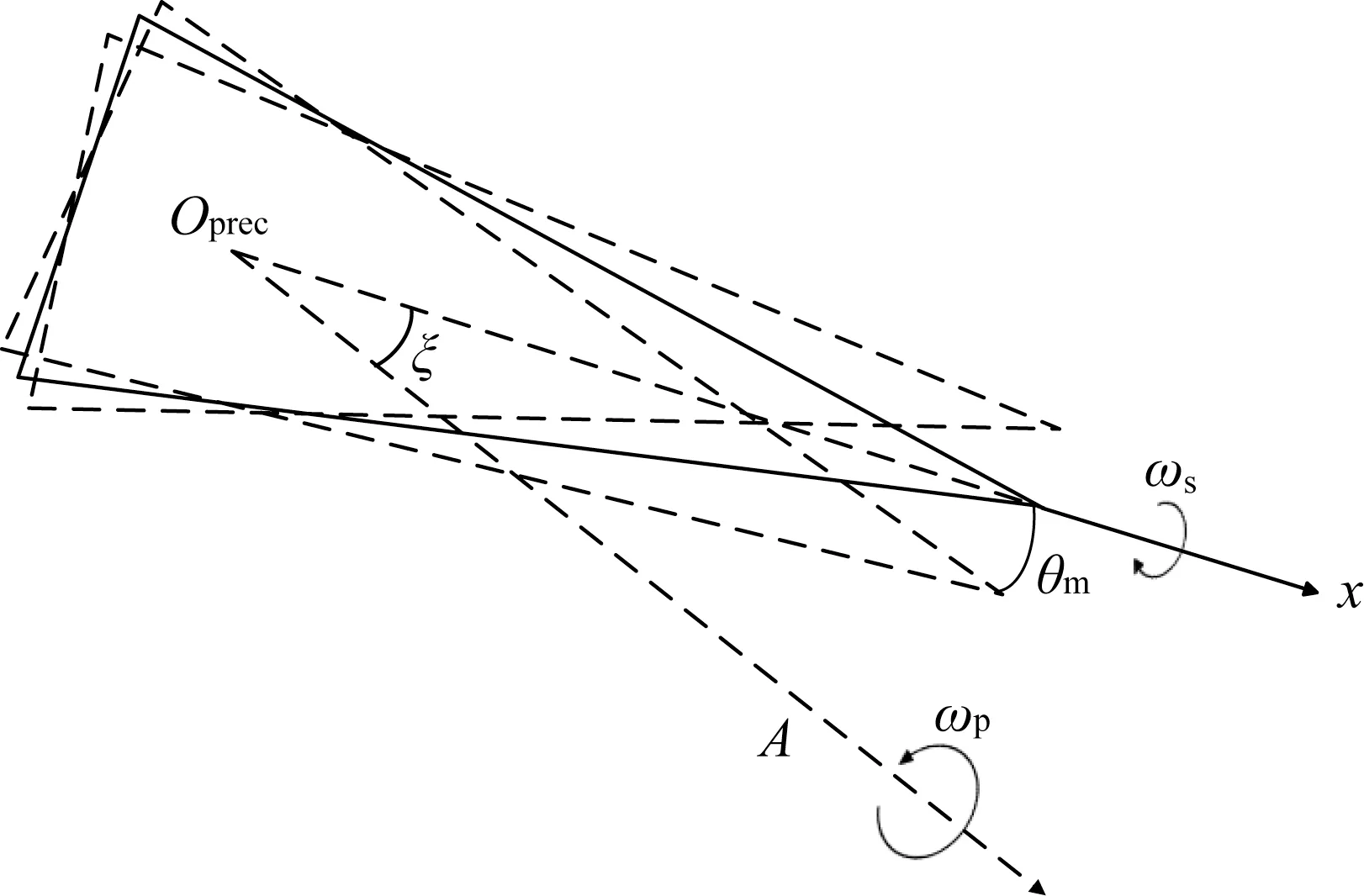
图2 章动Fig.2 Schematic diagram of nutation

式中：ωn为波动角度变化的角速度；θm为波动的最大角度，当导弹的锥形运动趋于稳定时，θm呈现为固定值［13］。

此时的章动角ξa=ξ+θnut，章动的产生使导弹对称轴具有了绕Oprec点的位于波动平面内的角速度ωnθmcos(ωntm)，其中tm为慢时间变量。

1.2 弹载雷达运动模型

考虑前视情形下进行俯冲，并具有自旋、进动以及章动的弹载雷达运动模型如图3 所示。设其初始时刻已自旋β0角度，锥旋α0角度。图中，Oap为此时的天线面板中心，虚线圈为天线面板中心在锥旋过程中的轨迹；Oap，ref为锥旋到最高处时Oap的位置；OprecA为锥旋时的旋转轴，自旋轴Oprecyprec绕OprecA进行旋转，两条旋转轴的交点为进动点Oprec；弹体的平动速度vap沿其锥旋轴方向；γ为导弹俯冲角，是锥旋轴OprecA与水平方向的夹角；ξa为锥旋轴与自旋轴之间的夹角；L1为进动点Oprec与天线面板中心Oap的距离；H为平台高度；ωs、ωp分别为弹体绕自旋轴Oprecyprec与绕锥旋轴OprecA旋转的角速度；φi、θi为地面散射点Pi相对于雷达阵列的下视角与方位角；d为相邻两接收通道间的距离；dn=，表示第n个接收通道与参考通道间的物理距离（选择第1 个方位接收通道作为参考通道），N为方位接收通道总数。

图3 复杂运动下弹载雷达平台运动模型Fig.3 Schematic diagram of the missile-borne radar platform motion model under complex motion situation

为分析方便，建立了进动坐标系Oprec-xprecypreczprec，其中Oprecyprec为弹体的对称轴线，Oprecxprec平行于天线面板的基线，Opreczprec由右手定则确定；建立了天线面板坐标系Oap-xapyapzap，Oapxap轴与进动坐标系的Oprecyprec重合，均为弹体的对称轴，Oapyap沿弹体的基线方向，Oapzap由右手定则确定；建立了地面场景坐标系O-xyz，其中z轴通过此时的天线面板中心Oap，y轴的位置使得锥旋轴OprecA位于平面zOy内，x轴由右手定则确定。

1.3 散射点斜距模型

为求解杂波的信号模型，需要计算在慢时间tm时刻散射点Pi距发射通道和第n个方位接收通道的双程瞬时斜距，公式如下：

式中：RT(tm)、RR，n(tm)分别为慢时间tm时刻散射点到发射通道与接收通道的单程瞬时斜距。

散射点在地面参考坐标系中的坐标可以表示为

式中：R0，i为初始斜距，且有关系H=R0，icosφi。

为计算式（2）的精确解析式，需将散射点转换到进动坐标系Oprec-xprecypreczprec中。

1.3.1 坐标转换

首先计算进动点Oprec在地面场景坐标系的坐标，从x轴正向看入，几何关系如图4 所示。

图4 空间坐标以x 轴投影到yOz 平面的关系Fig.4 Projection of the spatial coordinate into the yOzplane from the x-axis

其中，E点为天线面板中心锥旋时的轨迹圆圆心；点F为天线面板中心到线段Oap，refE的投影点；α0为天线面板中心距其最高参考点Oap，ref的旋转角度，即锥旋旋转角度。由图4 可知，Oprec的x轴坐标为

式中：α0为锥旋角度；ξa为锥旋轴与自旋轴之间的夹角。

由图4 中的几何关系，最终可得出Oprec在地面场景坐标系中的坐标为

式中：γ为导弹俯冲角，即锥旋轴OprecA与水平方向的夹角。

此时平移关系已经确定，将地面场景坐标系原点平移到进动点Oprec处，对于散射点Pi，其此时的坐标可表示为

坐标系因为俯冲及旋转关系，并未与此时平移后的地面场景坐标系重合。因此须首先将y轴旋转至锥旋的锥面上消除俯冲的影响，为此需要绕此时的x轴顺时针旋转γ-ξa角度。旋转后的y轴与OprecOap，ref重合，此时散射点的坐标为

考虑自旋的影响，自旋即绕y轴顺时针旋转，因此再将此时的坐标系绕y轴顺时针旋转β0角度，可得此时散射点的坐标为

式中：(x2，y2，z2)T、(x3，y3，z3)T为两个中间坐标。

最后考虑锥旋的影响，需绕锥旋轴OprecA逆时针旋转α0角度。OprecA并未在坐标轴上，此时的旋转矩阵需要借助罗德里格斯旋转公式的矩阵形式，一个坐标系绕单位矢量k=(kx，ky，kz)T逆时针旋转α0角度的旋转矩阵表达式为

式中：κ=1-cosα0。

求得此时坐标系中OprecA的单位矢量nOprecA，由简单的几何关系可得

因此，将式（10）代入式（9）可得锥旋的旋转矩阵ΜtrA完整表达式，将此时的坐标系以ΜtrA进行旋转即可转换到进动坐标系Oprec-xprecypreczprec中，有散射点的坐标为：

式中：ΜtrB为总的旋转矩阵，满足

在坐标转换完成后，以下计算发射与接收斜距均在进动坐标系Oprec-xprecypreczprec中求解。

1.3.2 发射斜距计算

首先求解发射斜距，自旋对发射通道无影响，因此发射通道的速度包括平动速度vap、锥旋线速度vp以及章动线速度vnut。其中vap的表达式为

式中：nOprecA为OprecA方向的单位矢量。

进动线速度vp的大小‖vp‖=ωpL1sinξa，方向沿天线面板中心轨迹圆的切线方向，与平动速度vap和矢量OapE垂直，可知OapE在进动坐标系中的单位矢量nOapE的坐标为

式中：β0为自旋角度。

可知发射通道进动速度的表达式为

在进动坐标系中，章动速度的方向垂直于yprec轴且在平面OprecOapA内，由式（1）可得其大小为‖vnut‖=ωnθmL1cos(ωntm)，因此发射通道章动速度的表达式为

式中：nnut为章动速度的单位方向矢量。

最终可得发射斜距的表达式为

1.3.3 接收斜距计算

第n个接收通道具有平动速度vap、自旋速度vs、锥旋速度vp，n与章动速度vnut，n，其平动速度与发射通道相同，自旋速度vs指向zprec轴，大小为ωsdn，即

求锥旋线速度vp，n需要求得旋转矢径。进动点Oprec到第n个方位接收通道点On的方向矢量在进动坐标系中的坐标为

从OprecOapA平面的视角看入，可得此时第n个接收通道在直线OprecE上的投影点En与E的距离为

由此得出第n个方位通道进动旋转中心En在进动坐标系中的坐标矢量为

因此第n个方位接收通道因锥旋产生的线速度vp，n表达式为

为求第n个方位接收通道因章动产生的线速度vnut，n，空间位置关系如图5 所示。

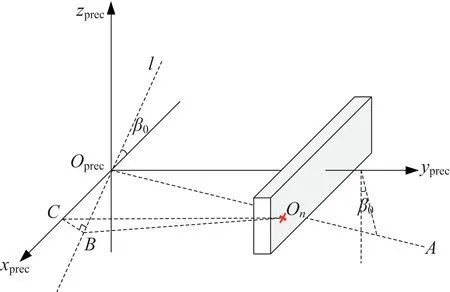
图5 第n 个接收通道章动旋转半径BOnFig.5 Schematic diagram of the nutation radius BOn of the nth receiving channel

由图可知，章动等效于自转轴绕1 条直线旋转（反复转动1 个微小的圆弧），其中位于平面xprecOpreczprec内的直线l是章动时天线面板的旋转轴，垂直于yprec轴和OprecA（即自转轴和锥旋轴），由On在xprec轴的投影C向直线l作垂线，交点为B，此时BC⊥l且OnC⊥l，BOn⊥l，因此第n个接收通道的旋转半径为BOn，章动速度垂直于BOn和l，表示式为

式中：nl为直线l的单位方向矢量。

最终可得接收斜距的表达式为

1.3.4 瞬时斜距模型

将式（17）与式（25）代入式（2），可得双程斜距的表达式为

2 信号模型的建立

假设弹载雷达采用线性调频（LFM）信号作为发射信号波形，即发射信号可表示为

式中：rect(·)为矩形窗；f0以载波频率为准；Te为传输信号的脉冲持续时间；为条频率，B为信号带宽。

在距离脉冲压缩后，对位于斜距为r的距离环内的地面散射点Pi，弹载雷达的第n个方位通道接收到的回波信号可以表示为

式中：Rn，i(tm)为杂波点和雷达平台之间的双程瞬时斜距，如式（26）所示；Ar，i为r-tm域中的回波信号振幅。

假设位于斜距为r的距离环上的杂波信号由Nc个杂波块组成，则第n个方位通道接收的总回波信号表达式为

考虑到弹载雷达系统中波束驻留时间相对较短，可以使用先验雷达系统参数近似补偿式（31）中的二次项［14］。在执行方位傅里叶变换（Fourier Transform，FT）之后，距离-多普勒域的回波信号表达式为

式中：σr，i为第i个杂波块在r-fa域的信号幅度；fa为多普勒频率变量。

根据式（26）和式（27），可得多普勒频率的表达式为

由式（33）可知，杂波多普勒频率不仅与平台的平动速度有关，还与自旋线速度、锥旋线速度、章动线速度等有关，同时因为旋转的关系，也与自旋角α0、锥旋角β0以及章动角ξa有关。因此，弹载平台的复杂运动将使杂波多普勒频率和空间角频率不再保持一一对应关系，这表明弹载雷达系统中的杂波将出现严重的非平稳现象。

3 仿真试验及结果分析

3.1 不同运动情形下杂波仿真结果

使用Morchin 散射模型［15］的高山地形对杂波进行仿真，将地面依据雷达的分辨率切分成细小的网格，将每一个网格视为单个的杂波点，实现对成片的分布式地面杂波进行仿真，其散射系数表达式为

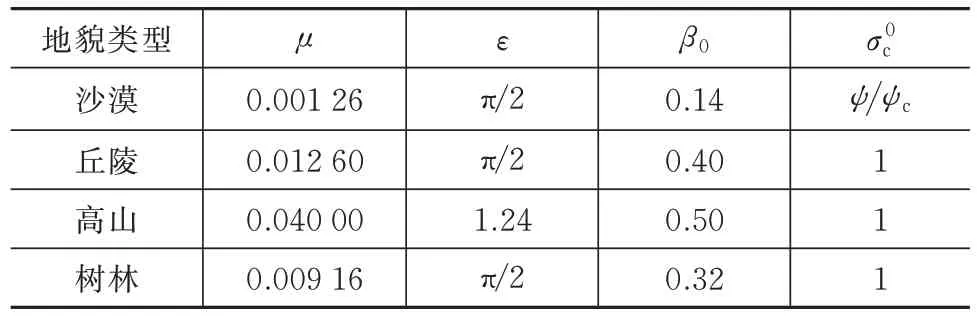
表1 Morchin 模型常数配置Tab.1 Constant configuration of the Morchin model

表2 弹载平台系统参数Tab.2 System parameters of the missile-borne platform

3.1.1 平飞前视运动

平飞前视弹载雷达下高山杂波的距离-多普勒谱和空-时二维功率谱如图6 所示。由图可知，对于前视雷达，多普勒谱中心随距离单元发生变化，呈现距离依赖性。由于主瓣杂波的多普勒频率大于旁瓣杂波，因此只有主瓣左边存在旁瓣。

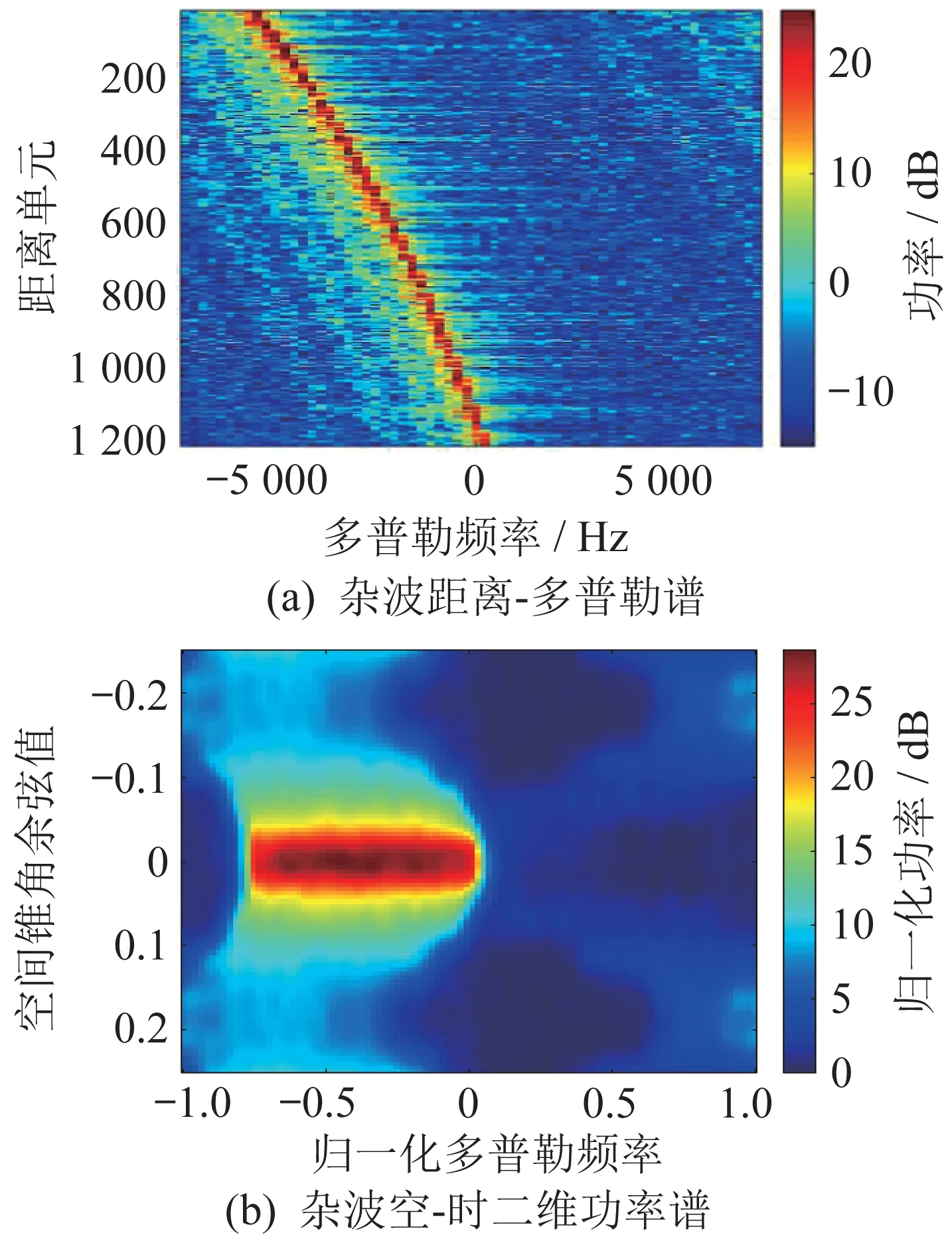
图6 平飞前视杂波仿真结果Fig.6 Simulation results of clutter in forward-looking and level flight case

3.1.2 俯冲前视

俯冲角γ为10°、20°和30°时高山杂波的距离-多普勒谱和空-时二维功率谱如图7 所示。当俯冲角等于俯仰角，即俯冲角为下视角的余角时，多普勒频率达到最大的173 kHz。俯冲角不等于俯仰角时，多普勒频率随角度差增大而减小，多普勒谱中心偏移，呈现距离依赖性。从空时谱中可见：当俯冲角等于俯仰角时，杂波谱扩散程度较轻；当俯冲角与俯仰角差距越大，多普勒频移随距离的变化程度越大，杂波扩散程度越剧烈。

3.1.3 俯冲前视附带进动以及章动运动

固定俯冲角为10°，自旋角度β0分别为15°、30°和45°的处理结果如图8 所示。

从距离多普勒谱可以看出，多普勒频率随着旋转角度增大出现扩展；从空时谱可看出，因旋转导致其不同距离单元的空间频率产生差别，与只有俯冲的前视情况下所有空间频率均为零的情形不同。

接下来固定俯冲角为10°，自旋角为15°，同时在不同的章动角ξa下变化锥旋角α0，仿真结果如图9 所示。由图可知，当ξa变大时，空-时二维谱的空间频率会发生变化，对多普勒频率的影响较小。自旋与锥旋均为旋转，因此带来的影响也大致类似，即多普勒频率扩展和空间频率发生变化。进动的引入除了使得多普勒谱向左扩展以外，还导致空-时二维谱中的空间锥角余弦值不再呈现关于空间角频率中心对称的关系，使得线性的杂波补偿方法可能失效，章动的引入则导致杂波的空-时二维谱在空间余弦方向发生偏移，使空间角频率中心进一步变化。

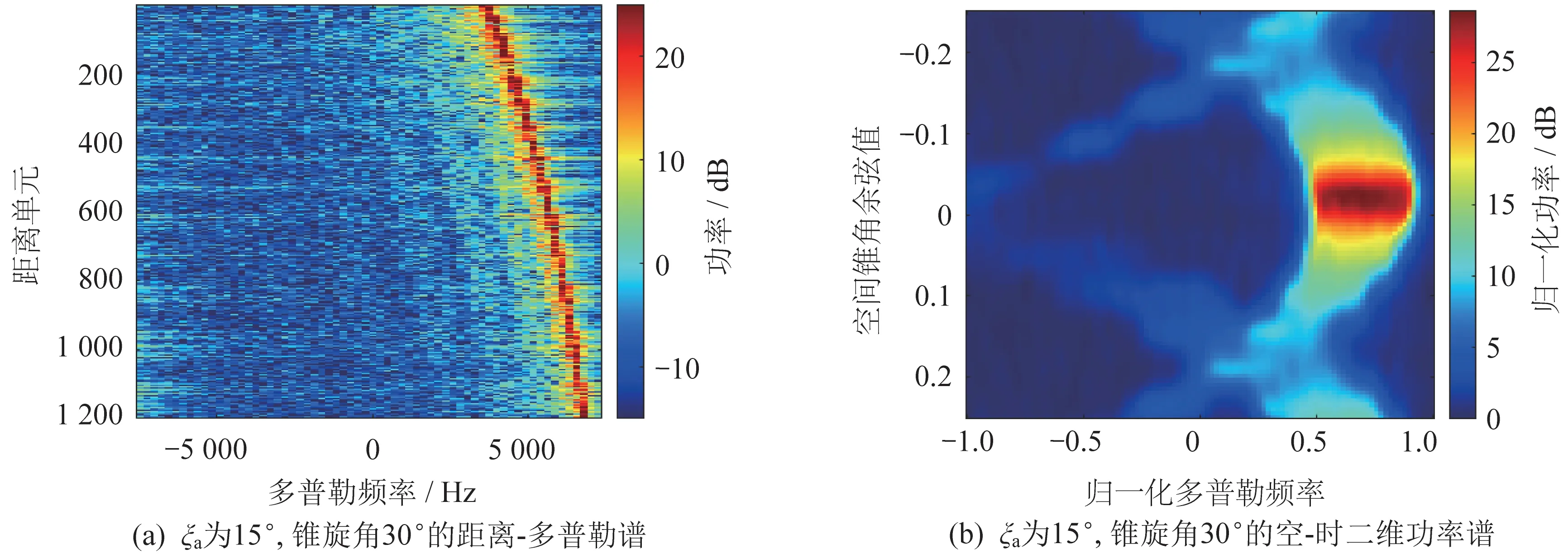
图9 不同锥旋角和章动角的杂波仿真结果Fig.9 Simulation results of clutter with different coning angles and nutation angles

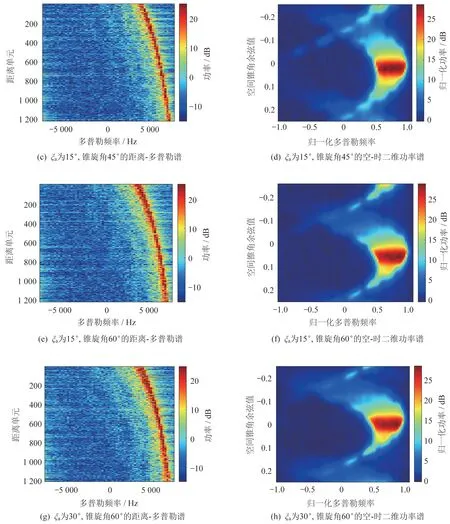
续图9 不同锥旋角和章动角的杂波仿真结果Continue Fig.9 Simulation results of clutter with different coning angles and nutation angles

3.2 结果分析

由3.1 节的仿真结果可知，在进动与章动存在的条件下，弹载平台与杂波间的径向速度不再只由弹体的平动速度决定，同时还引入了自旋速度、进动速度与章动速度，导致杂波的多普勒频率发生扩展，空间角频率因为旋转的关系也发生改变，不再聚集于零频，传统的只考虑平动的杂波模型对于具有复杂运动特性的弹载雷达将会因为不匹配其运动特性而产生较大的误差。

4 结束语

本文研究了基于弹载雷达平台复杂运动情形下的杂波建模方法，给出了较为精确的考虑俯冲、自旋、锥旋以及章动等各种运动情形下的弹载平台运动模型，并基于此推导了弹载平台的回波信号模型。仿真结果表明：本文所提的方法相比传统的平动杂波模型，更加适用于实际中复杂运动的弹载雷达，为后续对弹载雷达进行杂波补偿以及杂波抑制等处理打下了理论基础。