命题逻辑中一类扩展子句消去方法

刘凌荣, 陈树伟*, 吴贯锋

(1. 西南交通大学 数学学院, 四川 成都 610031; 2. 系统可信性自动验证国家地方联合工程实验室, 四川 成都 610031)

1 预备知识

子句集的简化是命题逻辑可满足性判定的重要研究方向,研究子句集冗余性质能提高求解器的求解能力和效率,可满足性判定过程中删除冗余子句，已被国内外学者广泛研究[1-4].目前，命题逻辑子句集的冗余性质的研究主要分为2种[5]:基于逻辑等价的冗余性质和基于可满足性等价的冗余性质.

早期基于逻辑等价的冗余子句的消去方法主要有恒真消去[6](tautology elimination)和包含消去[7](subsume elimination).Heule等[8]将隐藏和不对称概念与恒真和包含概念结合,提出了一系列逻辑等价的冗余子句消去方法,其中包括隐藏恒真子句消去方法(hidden tautology elimination,HTE)、不对称恒真子句消去方法(asymmetric tautology elimination,ATE)、隐藏包含子句消去方法(hidden subsumption elimination,HSE)和不对称包含子句消去方法(asymmetric subsumption elimination,ASE).

相比于基于逻辑等价的冗余性子句消去方法,可满足性等价的冗余性子句消去方法有更强的能力简化子句集.Jarvisalo等[9]提出了封锁子句消去方法(blocked clause elimination,BCE),该方法被嵌入到求解器预处理中,极大地简化了原始子句集,提高了求解器的求解效率.同年,Heule等[10]将封锁子句推广,提出了覆盖子句消去方法(covered clause elimination,CCE).Jarvisalo等[11]将归结原则和文献[8]中的冗余性质结合,发现若归结原则前置后,基于子句C的某个文字l的所有归结式都具冗余性质P,那么称子句C具性质RP,且性质RP仍然是冗余的,并且基于子句C的所有l-归结式都具有AT性质(即C具有RAT性质),广泛存在于求解器中作为预处理的一部分.Kiesl等[12]提出了集合封锁和语义封锁,该方法将封锁子句进一步推广,对于指派翻转也由一个文字演变为多个文字.Heule等[13]提出了传播冗余,该方法通过翻转子句的封锁指派来判断子句的冗余性.Heule等[14]利用传播冗余性质提出了SDCL(satisfaction-driven clause learning)求解框架.宁欣然等[15]将Kiesl等[16]提出的一阶逻辑上的蕴涵模归结合一原则降到命题逻辑,提出了基于命题逻辑的蕴涵模归结理论的子句消去方法,该方法的求解效率和求解能力均强于封锁子句.

以上研究都对求解器的发展起到了推动作用,虽然近十年来冗余性质的研究取得了很大的进展,但之前的子句消去方法都是通过研究子句本身在子句集中是否满足冗余条件,忽略了对所需要判断的子句添加冗余文字是否有助于满足冗余条件.事实上,添加冗余文字后的子句在子句集中更容易满足冗余条件.本文基于命题逻辑中冗余性的基础知识,在它们的基础上对需要判断的子句先进行冗余文字添加,通过隐藏或不对称文字添加方法提出一系列新的子句消去方法,如不对称归结包含消去(asymmetric resolution subsumption elimination,ARSE)、不对称归结不对称恒真消去(asymmetric resolution asymmetric tautology elimination,ARATE)和不对称集合封锁(asymmetric set blocked,ASETBC).最后,提出L-集合蕴涵模理论(L-setimplication modulo resolution，L-SETIMR)和L-不对称集合蕴涵模理论(L-asymmetric set implication modulo resolution,L-ASETIMR),并且证明了这些子句消去方法在命题逻辑上的可行性.

命题逻辑子句集的定义如下.在命题逻辑中,称原子及其否定为文字(literal)、子句(clause)为有限多个文字的析取,子句集为有限多个子句的合取,只含一个文字的子句被称为单元子句.用l表示文字,C表示子句,F表示子句集.真值指派是将文字映射到{0,1}上的函数,l在指派τ下为真，则有τ(l)=1,同时也有τ(┐l)=0；否则,l在指派τ下为假(指派τ弄假文字l),即τ(l)=0,同时也有τ(┐l)=1.若指派τ满足子句C(子句C在指派τ下为真),则τ至少满足子句C中的一个文字,指派τ满足子句集F当且仅当τ满足每一个子句.解释是对子句集中文字进行指派,当一个解释使得子句集F为真时,则称该解释是子句集F的一个模型(model).当子句集F的任意模型均为子句C的模型时,称F蕴涵(imply)C(记F|=C).显然,子句集F蕴涵它中的每一个子句C.2个子句集是逻辑等价的，当且仅当对于2个子句集在任意相同真值指派下具有相同的真值；2个子句集是可满足性等价的当且仅当2个子句集具有相同的可满足性[5].当一个子句同时包含文字l和文字┐l时,称该子句为重言式(恒真式)子句.若子句C1中所有的文字都在子句C2中出现,则称C1包含于C2(即C1⊆C2).记符号τl表示翻转指派τ中的文字l的真值,符号τL表示翻转指派τ中的文字集合L中所有文字的真值.Fl表示由子句集F中包含文字l的所有子句构成.FL表示由子句集F中至少包含一个文字l∈L的所有子句构成.若存在子句消去方法S1和S2,对任意相同子句集F分别使用子句消去方法S1和S2，得到简化子句集S1(F)和S2(F),若S1(F)⊆S2(F),则称子句消去方法S1至少与S2一样有效；若存在子句C∈S2但C∉S1,即S1(F)⊂S2(F),称子句消去方法S1比S2更加高效[10].

定义 1.1[8]给定命题逻辑子句集F及子句C∈F,隐藏文字添加子句HLA(F,C)是一个不断重复以下步骤得到的子句:子句C中包含文字l1∈C,子句集F{C}中存在二元子句l1∨l,则可将文字┐l添加到子句C中,即C:=C∪{┐l},此时,称┐l为子句C的隐藏文字(hiddenliteral).

定义 1.2[8]同上,不对称文字添加子句ALA(F,C)是一个不断重复以下步骤得到的子句:若子句C=l1∨l2∨…∨ln在子句集F{C}中存在子句C=li1∨li2∨…∨lik∨l(其中lij∈C,j=1,2,…,k),则可将文字┐l添加到子句C中,即C:=C∪{┐l},此时,称┐l为子句C的不对称文字(asymmetricliteral).

例 1.1考虑命题逻辑子句集F=(a∨b∨c)∧(a∨b∨d)∧(a∨┐d∨e),则对子句a∨b∨c进行不对称文字添加得到子句ALA(F,a∨b∨c)=a∨b∨c∨┐d∨┐e.

定理 1.1[15]在命题逻辑子句集中,若文字l为子句C的隐藏文字或不对称文字,则F{C}|=(C≡C∨l).

该定理说明子句C和子句C∨l在子句集中具有相同地位,即子句集F与子句集(F{C})∪{C∨l}保持逻辑等价.

定义 1.3[15]设子句C=C1∨l,子句D=D1∨┐l,称子句C⊗lD=C1∪D1为子句C和D的l-归结式(记⊗l为基于文字l的归结符号).

2 子句消去方法

2.1 保持逻辑等价的子句消去方法Heule等[8]提出表1所示的冗余性质P,基于冗余性质P得到的子句消去方法PE(PE为子句集中删去具有性质P的子句)是保持逻辑等价的,即简化后的子句集与原子句集保持在任意相同指派下仍具有相同的真值.

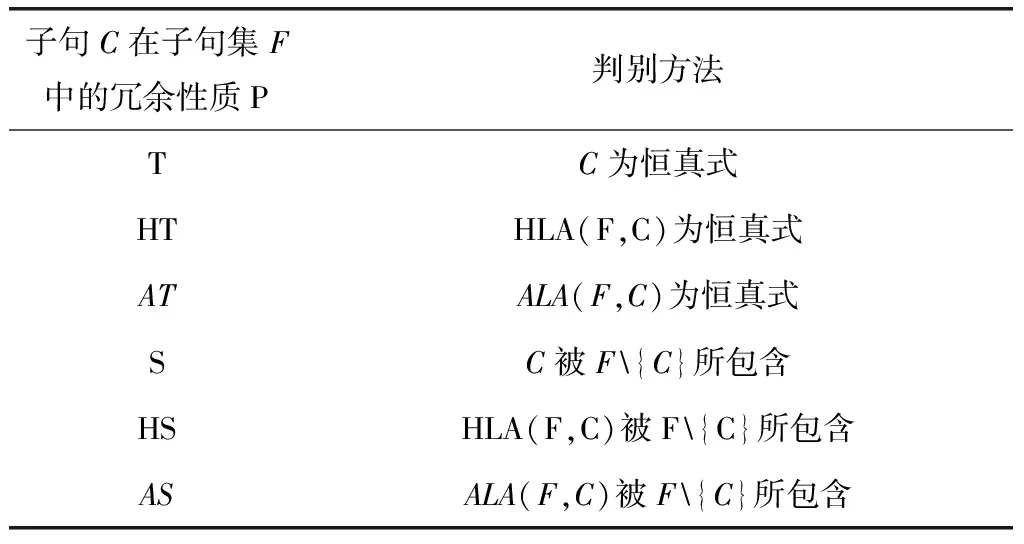
表 1 基于逻辑等价的冗余性质

2.2 保持可满足性等价的子句消去方法Jarvisalo等[11]将归结原则前置后提出了表2所示的冗余性质RP,基于冗余性质RP得到的子句消去方法RPE(RPE为删去具有性质RP的子句)是保持可满足性等价的,即删除具有性质RP的子句,简化后的子句集与原子句集具有相同的可满足性.

表 2 将归结原则前置所得到可满足性等价的冗余性质

综合表1和表2的性质,得到如图1所示的冗余性质有效传递图[11],箭头A指向B,表示冗余性质A比冗余性质B更加高效,即子句C在子句集F中具有性质B,那么它在子句集F中也一定具有性质A.

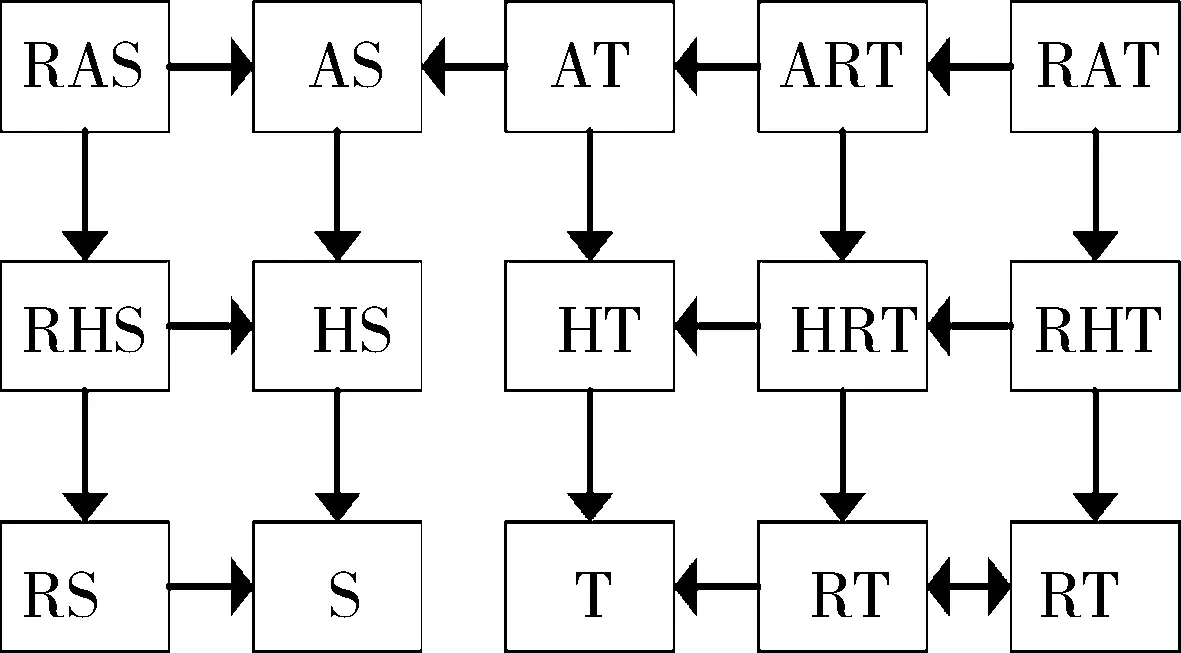
图 1 冗余性质有效性传递比较

2.3 扩展子句消去方法对比图1中的冗余子句判定方法,同样可以将需要判定的子句先进行隐藏或不对称文字添加得新子句,因为对子句进行隐藏或不对称文字添加后的子句集与原始子句集是逻辑等价的.因此,可以通过判断新子句是否具有图1的性质反过来确定原始子句的冗余性.因为隐藏文字是不对称文字的特殊形式,以下为方便叙述,将隐藏文字也视为不对称文字.

定义 2.1在命题逻辑子句集中,给定一个子句集F和一个子句C∈F,C具有性质ARS当且仅当(i)子句C在子句集F中具有表2中性质RS,或(ii)子句ALA(F,C)在子句集(F{C})∪ALA(F,C)中具有表2中性质RS.

定理 2.1在命题逻辑子句集F中,若子句C具有性质ARS,则子句集F与子句集F{C}可满足性等价.

证明假设子句C在子句集F中具有ARS性质.若在任意指派下,子句集F和子句集F{C}都不可满足,则子句C在子句集F中是冗余的.因此,现假设存在指派τ弄假子句C但满足子句集F{C}.指派τ弄假子句C,则对子句C进行不对称文字添加得到子句ALA(F,C).由定理1.1知,指派τ同样弄假子句ALA(F,C).由于子句C在子句集F中具有性质ARS,所以:(i)当子句C在子句集F中有性质RS时,子句C冗余;(ii)子句ALA(F,C)在子句集F{C}∪ALA(F,C)中具有性质RS,即子句ALA(F,C)中存在文字l,其所有的l-归结式均被子句集F{C}所包含,则翻转文字l的真值得到新指派τl既满足子句C,也满足子句集F{C}.因为翻转文字l的真值仅可能会弄假F┐l中的子句,但对于任意子句D∈F┐l,其l-归结式ALA(F,C)⊗lD被子句集F{C}所包含.由τ满足子句集F{C}知,τ满足子句ALA(F,C)⊗lD,由于子句ALA(F,C)⊗lD中不含文字l和┐l,所以指派τl满足ALA(F,C)⊗lD.又指派τl弄假子句ALA(F,C){l}中所有文字,所以指派τl满足子句D且也满足子句C.

定理2.1说明在命题逻辑子句集F中具有性质ARS的子句是冗余的,子句消去方法ARSE可以删去子句集中具有性质ARS的子句.

定理 2.2ARS性质比RS性质更高效.

证明ARS性质至少与RS性质一样高效.因为子句C⊆ALA(F,C),假设子句C的所有l-归结式为Rl(C)；子句ALA(F,C)的所有l-归结式为Rl(ALA(F,C)).同样满足Rl(C)⊆Rl(ALA(F,C)).因此,若Rl(C)中子句被子句集F{C}所包含,则Rl(ALA(F,C))中子句也一定被子句集F{C}所包含.此外,ARS子句不一定是RS子句,例如考虑如下子句集.

例 2.1在命题逻辑子句集中F={a∨b∨c,a∨x,b∨┐x∨e,┐x∨d∨f,┐e∨d∨g,┐a∨b∨d∨f∨g,┐a∨b∨d∨h∨g},设子句C=a∨b∨c,基于文字a,子句集F中有2个含有文字┐a的子句能与子句C进行归结,得到a-归结式为b∨c∨d∨f∨g和b∨c∨d∨h∨g,显然2个子句均不被子句集F{C}所包含.对子句C进行不对称文字添加的新子句ALA(F,C)=a∨b∨c∨┐x∨┐e,基于文字a,对子句ALA(F,C)与子句集F中子句进行归结,得到a-归结式为b∨c∨d∨┐x∨┐e∨f∨g和b∨c∨d∨┐x∨┐e∨h∨g,在子句集F{C}中存在子句┐x∨d∨f和┐e∨d∨g分别包含于2个a-归结式,这说明子句C具有ARS性质.

定义 2.2在命题逻辑子句集中,给定一个子句集F和子句C∈F,C具有性质ARAS当且仅当:(i)子句C在子句集F中具有表1中性质S,或(ii)子句ALA(F,C)在子句集(F{C})∪ALA(F,C)中具有表1中性质S或(iii)子句ALA(F,C)在子句集(F{C})∪ALA(F,C)中具有表2中性质RAS.

定理 2.3在命题逻辑子句集F中,若子句C具有性质ARAS,则子句集F与子句集F{C}可满足性等价.

证明假设子句C在子句集F中具有ARAS性质,且假设存在指派τ满足子句集F{C}但弄假子句C.对子句C进行不对称文字添加得到子句ALA(F,C),子句集(F{C})∪ALA(F,C)与子句集F逻辑等价.因此,指派τ同样弄假子句ALA(F,C).由于子句ALA(F,C)具有性质RAS,所以存在文字l∈ALA(F,C),使得ALA(F,C)⊗lF┐l中任意子句可以通过子句集F{C}中选取子句进行不对称文字添加后均被子句集F{C}所包含,即子句ALA(F,C)中存在文字l,其所有的l-归结式均被子句集F{C}所包含.由指派τ满足F{C}知,τ满足任意子句C1∈ALA(F,C)⊗lF┐l.因为指派τ弄假子句ALA(F,C)但满足子句C1,所以指派τ至少满足F┐l中子句的2个文字(其中一个文字为┐l).因为翻转指派τ中文字l的真值仅可能会弄假F┐l中的子句,但τ至少满足F┐l中子句的2个文字.因此,翻转指派τ中文字l的真值得到指派τl既满足子句集F{C}且也满足子句ALA(F,C),因此指派τl也满足子句C.

定义 2.3在命题逻辑子句集中,给定一个子句集F和子句C∈F,C具有性质ARAT当且仅当:(i)子句C在子句集F中具有表1中性质T,或(ii)子句ALA(F,C)在子句集(F{C})∪ALA(F,C)中具有表1中性质T,或(iii)子句ALA(F,C)在子句集(F{C})∪ALA(F,C)中具有表2中性质RAT.

例 2.2在命题逻辑子句集中,考虑子句集F={a∨b∨c,a∨x,a∨b∨e,┐a∨f∨h,┐x∨f∨g,┐e∨h∨┐g},在子句集F中对子句C=a∨b∨c进行不对称文字添加后得到子句C=a∨b∨c∨┐x∨┐e,对于子句a∨b∨c∨┐x∨┐e在子句集F{C}的所有a-归结式为b∨c∨┐x∨┐e∨f∨h,又子句b∨c∨┐x∨┐e∨f∨h在子句集F{C}中具有AT性质.因此,子句a∨b∨c在子句集F中为ARAT子句.

定理 2.4在命题逻辑中,对于子句集F和子句C∈F,若子句C具有性质ARAT,则子句集F和子句集F{C}可满足性等价.

证明现假设存在指派τ满足子句集F{C}但弄假子句C.对子句C进行不对称文字添加得到子句ALA(F,C),子句集F和子句集(F{C})∪ALA(F,C)逻辑等价.所以,指派τ弄假子句ALA(F,C).由于子句ALA(F,C)具有性质RAT,所以存在文字l∈ALA(F,C),使得ALA(F,C)⊗lF┐l中任何子句可以通过子句集F{C}中选取子句进行不对称文字添加后成为恒真子句,因此指派τ满足任意子句C1∈ALA(F,C)⊗lF┐l.因为指派τ弄假子句ALA(F,C)但满足子句ALA(F,C)⊗lF┐l,所以指派τ至少满足F┐l中子句的2个文字(其中一个文字为┐l).因为翻转指派τ中文字l的真值仅可能会弄假中F┐l的子句,但τ至少满足F┐l中子句的2个文字.因此,翻转指派τ中文字l的真值得到指派τl既满足子句集F{C}且也满足子句ALA(F,C),因此指派τl也满足子句C.

定理 2.5在命题逻辑子句集F中,ARAT性质与RAT性质一样高效.

证明如果子句C具有性质RAT,对子句C进行不对称文字添加得到子句ALA(F,C),必然满足C⊆ALA(F,C).因此子句C在子句集F中具有的RAT性质,子句ALA(F,C)也必然具有.说明ARAT性质至少与RAT性质一样高效.反过来,若子句C具有ARAT性质,对子句C进行不对称文字添加后的到子句ALA(F,C),存在文字l∈ALA(F,C),其所有的l-归结式具有性质AT.1) 若归结文字l∈C,则可以通过与子句C进行l-归结的子句D,对Rl(C)添加不对称文字l,此时,说明C⊆Rl(C)∪{l}； 2) 若归结文字l∈ALA(F,C){C},则在子句集F{C}中至少存在一个子句D,子句D中包含文字┐l且满足子句ALA(F,C)中的不对称文字l是通过子句D添加所得,于是ALA(F,C)⊗lD⊆ALA(F,C),这说明若子句ALA(F,C)⊗lD具有性质AT,则子句ALA(F,C)也为恒真式.由1)和2)知,RAT至少与ARAT一样高效.

由定理2.5知,在子句集中ARAT性质和RAT性质高效性一样,但ARATE子句消去方法是先对子句进行不对称文字添加,再删除具有性质RAT的子句.因此,在冗余文字添加过程中可以通过表1中的冗余性质P删除子句集中部分冗余子句,从而避免了对子句选取文字进行归结.

定理 2.6在命题逻辑子句集中,ARAT冗余性质比ARAS性质更高效.

证明假设在子句集F中,子句ALA(F,C)基于文字l∈ALA(F,C)具有RAS性质,则子句ALA(F,C)基于文字l∈ALA(F,C)具有性质RAT.因为,任取子句C1∈ALA(F,C)⊗lF┐l,子句C1具有性质AS,即子句C1可以通过子句集F{C}中子句添加不对称文字得新子句ALA(F,C1),且在F{C}中至少存在一个子句D使得D中文字均在子句ALA(F,C1)中出现,即D中任意文字的非均为子句ALA(F,C1)的不对称文字,说明子句ALA(F,C1)具有性质AT.因此,子句C具有性质ARAS就一定具有性质ARAT,但ARAT子句不一定是ARAS子句,例如子句集F={a∨┐a},子句a∨┐a是恒真子句,因此具有性质ARAT.显然,子句a∨┐a不是ARAS子句.

定义 2.4[15]在命题逻辑子句集F中,若子句C基于文字l∈C的所有l-归结式被F{C}所蕴涵,则称子句C为蕴涵模归结子句,满足蕴涵模归结原则(implication modulo resolution,IMR).

下文将提出基于不对称文字添加的蕴涵模归结原则.

定义 2.5设在命题逻辑子句集F中,基于子句C,对子句C进行不对称文字添加得到子句ALA(F,C),若子句ALA(F,C)基于文字l∈ALA(F,C)的所有l-归结式被F{C}所蕴涵,则称子句C为不对称蕴涵模归结子句,满足不对称蕴涵模归结原则(asymmetricimplicationmoduloresolution,AIMR).

定理 2.7在命题逻辑子句集中,满足不对称蕴涵模归结原则的子句是冗余的.

证明设在子句集F中,基于子句C∈F,假设存在指派τ弄假子句C但满足子句集F{C}.先对子句C进行不对称文字添加得到子句ALA(F,C),显然τ弄假子句ALA(F,C).由子句C满足不对称蕴涵模归结原则知,所以存在文字l∈ALA(F,C)使得所有l-归结式被F{C}所蕴涵.由τ满足子句集F{C}知,对于任意子句D∈F┐l,指派τ满足ALA(F,C)⊗lD,则τ至少满足子句D中2个文字(其中一个为┐l),因为翻转文字l的真值仅可能会影响子句集中包含文字┐l的子句,因此τl至少满足子句D中一个文字,所以指派τl满足子句集F{C}∪ALA(F,C),所以指派τl满足子句集F.

3 不对称文字前置与文字集合翻转相结合

3.1 不对称文字前置与集合封锁理论相结合命题逻辑集合封锁子句消去方法是Kiesl等[12]提出的,其将封锁子句理论中单个文字真值的翻转提升到多个文字真值的翻转,与封锁子句相比该方法能够更加有效的缩减子句集的规模.

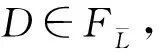
下边将给出基于不对称文字前置的集合封锁理论.

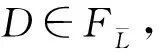
定理 3.1在命题逻辑子句集中,不对称集合封锁子句(ASETBC)是冗余子句.

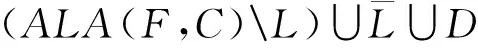
1) 若┐l∈D,即D为恒真式,则翻转文字集合L的真值不影响子句D的真值.

2) 若┐l∈(ALA(F,C)L),由τ弄假子句ALA(F,C)知,τ(┐l)=0,即τ(l)=1.翻转文字集合L的真值不影响文字┐l的真值,即τL(l)=1.由子句D中含有文字l知,翻转文字集合L的真值不会弄假F{C}中子句D.

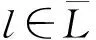
因此翻转文字集合L得到新指派τL满足子句集F{C}∪ALA(F,C),再由子句集F与子句集F{C}∪ALA(F,C)逻辑等价知,翻转文字集合L也满足子句集F.

定理 3.2不对称集合封锁子句(ASETBC)比集合封锁子句更高效.

证明由于不对称集合封锁子句是在集合封锁子句的基础上添加不对称文字,因此,若一个子句C在子句集中具有性质SETBC,那么该子句一定具有性质ASETBC.但若子句具有性质ASETBC,该子句不一定是SETBC子句,如例3.1所示.

例 3.1在命题逻辑子句集中,考虑F1={a∨b,b∨x,x∨b∨┐a,┐b∨┐x,┐b∨a}.对子句集F1中a∨b进行不对称文字添加得到子句集F2={a∨b∨┐x,b∨x,x∨b∨┐a,┐b∨┐x,┐b∨a}.由定义3.1知,子句集F1中子句a∨b不是集合封锁子句,但在子句集F2中子句a∨b∨┐x是集合封锁子句,所以子句a∨b在子句集F1中为不对称集合封锁子句.

3.2 不对称文字前置与L-集合蕴涵模理论相结合

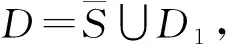
定理 3.3在命题逻辑子句集F中,若子句C在子句集F中满足L-集合蕴涵模归结原则,则子句C是冗余的.

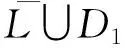
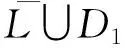
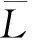
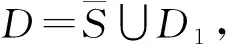
定理 3.4在命题逻辑子句集F中,若子句C在子句集F中为L-集合封锁,当且仅当子句集C在子句集F中为集合封锁.

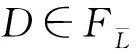
必要性 若子句C在子句集F中为L-集合封锁子句,则子句C一定是集合封锁子句.

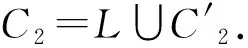
定理 3.5在命题逻辑子句集中,若子句在子句集中为L-不对称集合蕴涵模归结子句,那么该子句在子句集中冗余.

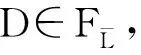
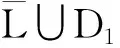
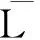
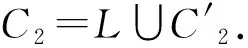
定理 3.6若子句在子句集中为L-不对称集合封锁子句,那么该子句在子句集中冗余.

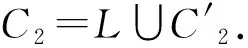
定理 3.7若子句在子句集中为L-不对称集合包含子句,那么该子句在子句集中冗余.

4 结束语

通过对子句集中的选取子句进行逻辑等价处理,根据不对称文字添加后的子句在子句集中是否冗余,反过来确定原子句在子句集中的冗余性.将该方法与冗余性质RP的子句相结合,提出了多种性质,并证明了子句集中这样性质的子句是冗余的,即消去具有这样性质的子句后,与原始子句集是可满足性等价的.之后,将该方法分别与命题逻辑蕴涵模归结原则(IMR)和集合封锁(SETBC)相结合,提出了不对称蕴涵模归结原则(AIMR)、不对称集合封锁(ASETBC).最后,提出了L-集合蕴涵模归结原则(L-SETIMR)和L-不对称集合蕴涵模归结原则(L-ASETIMR).目前本文只是在理论层面提出了一系列冗余子句消去方法,在未来研究中将这些方法实现于求解器预处理中,以期提高求解器的效率.