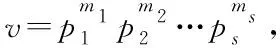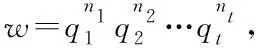跳频序列部分汉明相关理论界及其最优构造
周正春
(西南交通大学 数学学院, 四川 成都 610031)
1 前言
跳频多址技术目前广泛应用于超宽带(UWB)、军事通信和蓝牙等现代通信系统中.跳频序列是跳频多址通信系统的一个组成部分[1].例如,在多接入跳频分组无线网络中,每个发送器被分配一个唯一的签名序列,以控制无线电在一帧内为连续的分组使用的频率.在帧异步和包同步的假设下,当2个或多个无线电以相同的频率同时发送它们的包时,碰撞的包有可能互相破坏.这些碰撞可以通过数字签名序列的汉明相关来测量.为了减小频率冲突引起的多址干扰,必须减小所采用的跳频序列的汉明相关.
一般来说,跳频序列的汉明相关大致可分为3种类型[2]:周期汉明相关、非周期汉明相关和部分汉明相关.跳频序列的周期汉明自相关的研究可以追溯到著名的Lempel-Greenberger界[3].在2004年,Peng和Fan[4]推导了跳频序列集的周期汉明相关的界.文献[5-6]报道了关于周期汉明相关的跳频序列集的编码理论界.在过去的40 a中,已经有许多文献(如文献[3,6-15])达到了这些界的跳频序列的构造.
在实际应用中,跳频序列集的周期相关性决定了系统中可适应用户的数量和容错率[16],而它的非周期性和部分周期相关性影响它在接收端的同步和捕获性能[16-17].如上所述,关于跳频序列集的周期汉明相关性已有大量的研究,但是对于非周期相关和部分相关却知之甚少,而这些性质在理论意义和实际应用中都很重要.特别地,在同步时间有限或硬件复杂的许多应用程序场景中[17],相关窗口的长度应该比选定的跳频序列的周期短得多[4,17].同时,根据信道条件,窗口长度可能会随时间变化而变化.因此,我们希望所采用的跳频序列应具有良好的部分汉明相关性.
已有的跳频序列(集)部分汉明相关的理论界主要分为2种:
一是给定频率数目和序列长度条件下的部分汉明相关理论界.2004年,Eun等[17]建立了单个跳频序列的最大部分汉明自相关的下界.2012年,Zhou等[2]将Peng-Fan界推广到了部分汉明相关的情形,得到了跳频序列集最大部分汉明相关的下界.2014年,Cai等[18]改进了上述理论界,分别给出了单个跳频序列和跳频序列集的最大部分汉明相关的下界.
二是限定部分汉明相关条件下的序列数目的理论界.2016年,Cai等[19]从纠错编码的一些经典界出发,得到了在限定部分汉明相关条件下的序列数目的2个上界.此外,2010年,Niu等[20]发现了低碰撞跳频序列集的最大部分汉明相关的理论界.
下面介绍跳频序列部分汉明相关的研究进展.2004年,Eun等[17]提出一类具有最优部分汉明自相关的跳频序列的构造.Udaya等[12]基于多项式剩余类环上的m序列和Gordon-Mills-Welch序列提出了一类具有最优部分汉明自相关的跳频序列的构造.2012年,Zhou等[2]基于阵列结构提出一类具有严格最优部分汉明自相关的单个跳频序列和一类具有严格最优部分汉明相关的跳频序列集的构造.2012年,Niu等[21]基于广义m序列和广义Gordon-Mills-Welch序列提出了一类最优部分汉明相关的跳频/跳时序列集的构造.2014年,Cai等[18]基于广义分圆提出了一类强最优部分汉明相关的跳频序列(集)的构造.2016年,Cai等[19]提出一类具有最优序列集大小的强最优部分汉明相关跳频序列集的构造.2016年,Fan等[22]基于不相交循环完美Mendelsohn差族提出一类强最优部分汉明相关跳频序列的构造.2016年,Bao等[23]基于多重可划分平衡嵌套循环差填充提出几类强最优部分汉明相关跳频序列(集)的构造.2019年,Liu等[24]基于可划分差填充提出几类强最优部分汉明相关跳频序列(集)的构造.此外,2018年,Liu等[25]提出2类具有严格最优部分汉明相关的低碰撞区跳频序列集的构造.2019年,Han等[26]利用交织技术提出一类具有严格最优部分汉明相关的低碰撞区跳频序列集的构造.
2 基本概念
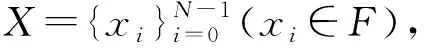
S={X1,X2,…,XM}.
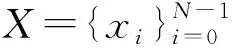
τ=0,1,…,N-1,
其中〈x〉n是x模N的最小非负余数,
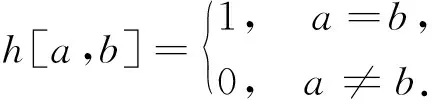
当X=Y时,称HXY(τ)为周期汉明自相关;当X≠Y时,称HXY(τ)为周期汉明互相关.
对于任意给定的跳频序列集S,最大汉明自相关Ha(S)、最大汉明互相关Hc(S)和最大汉明相关Hm(S)分别定义为:
Ha(S)=max{HXX(τ)|X∈S,0<τ Hc(S)=max{HXY(τ)|X,Y∈S,X≠Y, 0≤τ Hm(S)=max{Ha(S),Hc(S)}. 为简单起见,本文用(N,q,Ha)表示定义在大小为q的频隙集F上、长度为N的、最大汉明自相关为Ha的跳频序列,其中 Ha={HXX(τ):1≤τ 用(N,M,q,Hm)表示一个大小为q的频隙集上长度为N的M个跳频序列组成的集合,其最大汉明相关为Hm=Hm(S). 2.2 部分汉明相关函数 (1) 其中,0≤τ,j≤N-1,1≤L≤N. 特别地,如果L=N,j=0,(1)式就是周期汉明相关;如果L=N-τ,j=0,则(1)式就是非周期汉明相关函数. 当X=Y时,HX,X(τ;j|L)称为X的部分汉明自相关函数;当X≠Y时,HX,Y(τ;j|L)称为X和Y的部分汉明互相关函数. 定义 2.3对于F上任意2个不同的序列X和Y,任给整数L(1≤L≤N),它们的最大部分汉明自相关函数Pa(L)和最大部分汉明互相关函数Pc(L)分别定义为 和 设S是F上长度为N的M个跳频序列组成的集合,对于任给的相关窗长L,序列集S的最大部分汉明相关函数Pm(L)定义为 跳频序列的参数(长度、频隙集大小、最大相关值、序列集合大小)相互制约,本节主要介绍这些参数的理论界. 3.1 给定频率数目和序列长度条件下的部分汉明相关理论界在2004年,Eun等[17]发现跳频序列的最大部分汉明自相关下界. 定理 3.1(Eun-Jin-Hong-Song界[17]) 设X是大小为q的字母集F上的一条长度为N的跳频序列,那么对于任意的相关窗长L(1≤L≤N),有 (2) 其中,r是N模q的最小非负余数. 当L=N时,(2)界恰好是Lempel-Greenberger界[3]. 2014年,Cai等[18]改进(2)界,得到了如下结果. 推论 3.1(Cai-Zhou-Yang-Tang界[18]) 设X是大小为q的频隙集F上的一条长度为N的跳频序列,则对于任意的相关窗长L(1≤L≤N),有 (3) 其中,r是N模q的最小非负余数. 在实际系统中,相关窗口长度可能会根据信道条件的不同而变化.因此,希望跳频序列对任何窗口长度都具有最佳的部分汉明相关性. 定义 3.1令X是F上长度为N的跳频序列,如果对于任意相关窗长L(1≤L≤N),(3)界等号成立,则称X为强最优的. 当L=N时,(2)和(3)界恰好是Lempel-Greenberger界.显然,任何强最优跳频序列关于Lempel-Greenberger界也是最优的,但反之不然. 2012年,Zhou等[2]将Peng-Fan界推广到部分汉明相关的情形,得到如下结论. (4) 和 (5) 2014年,Cai等[18]改进了(4)和(5)界,得到下面的推论. (6) 和 (7) 显然,当L=N时,定理3.2和推论3.2中的界恰好是Peng-Fan界[4].这就表明,强最优跳频序列集关于Peng-Fan界也是最优的;反之不然. 虽然“每日优鲜”承诺两小时送达,现在甚至90%的订单都能在1小时内送达,但对于距离前置仓较远的的订单,不少顾客反映自己下单的产品在次日都未能送达。 3.2 限定部分汉明相关条件下的序列数目上界2009年,Ding等[5]基于经典的编码理论界,得到跳频序列集的周期汉明相关理论界.受Ding等[5]思想的启发,Cai等[19]提出在限定部分汉明相关条件下的序列数目的上界. 设S是F上长度为N的M个跳频序列组成的集合.Pm(L)表示S在所有长度为L的相关窗上的最大部分汉明相关函数.对于任意给定的L(1≤L≤N),将S中所有长度为L的子序列放在一起,得到一个F上参数为(L,NM,L-Pm(L);l)纠错码CS(L),其中 CS(L)={(ai,a〈i+1〉N,…,a〈i+L-1〉N): {a0,a1,…,aN-1}∈S,0≤i≤N-1}. (8) 将Plotkin界和Singleton界[27]应用到(8)式的纠错码CS(L)中,可得定理3.3. 定理 3.3[19]设S是由大小为q的频隙集上的长度为N的M个跳频序列组成的集合,则有 L>q·Pm(L)} (9) 和 (10) 一个很自然的问题是,已知的强最优跳频序列集对于(9)或(10)界是否也有最优的序列族大小?下面的定理给出了肯定答案. 定理3.5表示,当r≥2时,文献[2]中的强最优跳频序列集关于(9)界是紧的;当r=2时,关于(10)界也是紧的. 定义 3.2[17]如果对于任意的相关窗长L(1≤L≤N),(2)界等号成立,则跳频序列X∈F称为严格最优的. 当L=N时,(2)界恰好是Lempel-Greenberger界.因此,任何严格最优的跳频序列,关于Lempel-Greenberger界也是最优的;反之不然.文献[17]的跳频序列关于Lempel-Greenberger界最优,但不是严格最优的. 类似于3.2中严格最优跳频序列的定义,严格最优跳频序列集定义如下. 定义 3.3[4]如果对于任意的相关窗长L(1≤L≤N),(4)或者(5)界等号成立,则跳频序列集S是严格最优的. 当L=N时,(4)和(5)界正好是Peng-Fan界.因此,任何严格最优跳频序列集关于Peng-Fan界也是最优的;反之不然. vb(t)=(Trqn/q(b0αt),Trqn/q(b1αt),…,Trqn/q(bk-1αt)). (11) 当n=2时,定理4.1给出了文献[17]相同的参数;当n>2时,定理4.1的参数是新的. ub(t)=(Trqn/q(b0βt),Trqn/q(b1βt),… (12) 定义序列集 (13) 4.2 第二类最优部分汉明相关跳频序列集设p是素数,且q=pm,r、k是正整数且满足k|r,f(x)是GF(q)上的r次本原多项式,α是f(x)的根.设l是一正整数,且满足l|(qr-1)和gcd(r,l)=1.定义 3) 构造跳频序列集S={su,0≤u≤l-1}. 定理 4.3[21]由构造4.1生成的跳频序列集S具有以下性质: 本节先回顾一下广义分圆的基本理论,然后介绍一类基于广义分圆的强最优部分汉明相关跳频序列(集)[18]. pi-1=efi, 且集合 对于任意的Iv1=(i1,i2,…,iπ(v1))∈Ψv1,定义 (14) (15) 定义集合 且Iv1∈Ψv1}∪{{0}}. (16) Δ(x)=〈i〉e, (17) (18) ii)S关于(6)和(7)界是强最优的; iii)S中的每一条序列Si关于(3)界都是强最优的. 构造 6.1[19]令m和n是2个正整数且满足gcd(m,n)=1. (19) (20) t1=〈t〉n,t2=〈t〉m. 基于构造6.1,可以得到如下结论. 定理 6.1[19]定义序列集 (21) 1)S是由Fpr上长度为p(pr-1)的pr-1个跳频序列组成的集合; 3) 集合S关于(6)和(10)界都是最优的. CPMDF[30-31]由Fuji-Hara和Miao在构造最优光正交码时首次提出.首先,回顾CPMDF的定义. 基于不相交CPMDF,可得如下结论. (22) 其中,0≤t1<(v-1)/k,0≤t2 下面利用循环群中的差分矩阵提出一个不相交(v,k,1)-CPMDF的递归构造. 定理 7.2[22]设u和v是2个正整数.如果存在一个不相交的(u,k,1)-CPMDF、一个不相交的(v,k,1)-CPMDF以及一个(v,k+1,1)-CDM,则存在一个不相交的(uv,k,1)-CPMDF. 定理 7.3[22]设v和k是2个正整数.如果v和k满足以下条件之一: 根据定理7.1中给出的强最优跳频序列与不相交CPMDF之间的联系,可以得到如下结论. 推论 7.1[22]设v和k是2个正整数,当v和k满足定理7.3的3个条件之一时,则存在定义在大小为v的频隙集上的长度为kv的强最优跳频序列. 8.1 一类强最优跳频序列2004年,Fuji-Hara等[33]指出跳频序列与可划分循环差填充(CDP)之间的联系.基于此,文献[23]给出几类强最优跳频序列的构造. 使得 其中 K={|Br|:0≤r≤l-1}. 如果n=8a+1,则 B0={0,4a+1,8a},B1={4a-1,4a}, B1+r={r,2a-2+2r}, 1≤r≤a, Ba+1+r={a+r,2a-1+2r}, 1≤r≤a-1, B2a+r≡B1+r+4a+1(mod n), 1≤r≤2a-1. 如果n=8a+3,则 B0={0,4a+1,4a+2},B1={2a,6a+3}, B2={2a+1,6a+1}, B3={6a+2,6a+4}, B3+r={r,4a+1-r}, 1≤r≤2a-1, B2a+2+r≡B3+r+4a+2(mod n), 1≤r≤2a-2. 如果n=8a+5,则 B0={0,4a+2,4a+3}, B1={2a+1,6a+5}, B2={2a+2,6a+3},B3={1,6a+4}, B3+r={2a+2+r,6a+3-r}, 1≤r≤2a-1, B2a+2+r≡B3+r+4a+3(mod n), 1≤r≤2a-1. 如果n=8a+7,则 B0={0,4a+3,4a+4}, Br={r,2a+2r}, 1≤r≤a+1, Ba+r={a+1+r,2a+1+2r}, 1≤r≤a, B2a+r≡Br+4a+4(modn), 1≤r≤2a+1. 利用分圆类构造可分解的CRDFs,可以得到强最优的跳频序列. 5) 存在一个强最优的(6p,2;2p+1)跳频序列,其中p≡5(mod 8)是素数. 8.2 强最优跳频序列集的组合构造2009年,Ge等[34]给出跳频序列集与可划分平衡嵌套循环差填充(BNCDP)之间的联系.基于上述用于设计强最优跳频序列的组合方法,文献[23]给出强最优跳频序列集的组合构造. 下面利用分圆类得到一类具有特殊性质的可划分BNCDPs,并由此得到一类新的强最优跳频序列集的构造. K0=…=Kf-1={e}. 推论 8.1[18]设参数v、e、f与引理8.1中的假设相同,则存在一个强最优的(ev,f,e;v)跳频序列集S,其部分汉明相关为 8.3 强最优跳频序列集的两类递归构造第一个递归构造是基于循环差分矩阵(CDM)[23]的. 下面是第二类递归结构. 本节介绍一类强最优跳频序列集的构造方法[24]. 1≤τ≤N-1, 其中,Bi+τ={b+τ(mod N):b∈Bi}. Γ(B,τ)={(x,y):x-y≡τ(mod N),x,y∈B},1≤τ≤N-1. (23) i=0,1,…,q-1}, (24) 下面构造几类PDPs. B0={0,q+1,q-2}, Bj={j,2q+2-j}, B0={0,q+2,q}, B1={q+3,q+4},B2={1,2,2q+2}, B6={2q-2,6,2q+3}, Bq-4={q-4,q+8,q+1}, j≠q-4. B0={0,q+4,q+2}, B1={q+5,q+6}, B2={1,2,2q+6}, B3={q,q+8}, B6={6,2q+2,2q+7}, B12={12,2q-4,3}, B14={14,2q-6,2q+5}, Bq-10={q+18,q-10,q+1}, Bq-8={q+16,q-8,q+7}, Bq-2={q+10,q-2,q+3}, Bi={i,2q+8-i}, 4≤i≤q-1, i≠6,12,14,q-10,q-8,q-2. Bi0,i1,…,im-2={i:Tr(αi)=i0,Tr(αi+1)=i1,…, Tr(αi+m-2)=im-2,i=0,1,…,qm-2}. (25) (26) (27) χ(x1,x2)=x, B0,0={χ(0,k)f+m:k=0,1,…,e-1,m=0,1,…,f-1} (28) 和 Bi,j={χ(ihmgk,j+k)f+m: k=0,1,…,e-1,m=0,1,…,f-1}. (29) B={pm-1(pm-1)u+v:u=0,1,…,p-1, v=0,1,…,pm-1-1}, 0≤b≤pm(pm-1)-1,b∉B},i∈GF(pm). 9.1 强最优跳频序列的设计本节给出了一类强最优跳频序列的构造. s=(s0,s1,…,s(ξ-1)N-1), 其中 0≤i≤q-1, 0≤j≤ei-1, 0≤v≤ξ-2. 对于构造9.10生成的跳频序列,有以下结果. 定理 9.10[24]当l=1时,由构造9.10生成的跳频序列s是一个((ξ-1)N,qξ,Ha)跳频序列,且最大部分汉明自相关为 其中k=1,2,…,Ha. 定理 9.11[24]通过选择不同的PDPs,可以得到下列强最优跳频序列: 2) 在构造9.4中选择一个大小为q的[2q+4,{2,3},2]PDP,由构造9.10可以得到一个 ((ξ-1)(2q+2),qξ,2) 3) 在构造9.5中选择一个大小为q的[2q+8,{2,3},2]PDP,由构造9.10可以得到一个 ((ξ-1)(2q+8),qξ,2) 9.2 无限类强最优跳频序列的设计在本节中,基于构造9.10,下面给出强最优跳频序列的递归构造. 定理 9.13[24]对于l=1,如果 (30) 那么,由构造生成的跳频序列s,s1,s2,…,su都是强最优的. 根据构造9.12,得到以下结果. 定理 9.14[24]通过选择不同的PDPs,可以得到以下强最优跳频序列集: 3) 在构造9.8中选择一个大小为pm的[pm(pm-1),{pm-1},p]PDP,由构造9.10可以生成一个大小为pmξ的[pm(pm-1)(ξ-1),▽′,p]PDP.那么,由构造9.12生成一个 (p(pm-1)(ξ-1),pm-1,pmξ,p) ξ≥2m-1(2m-1), 且m≥3,则S4是强最优的. 跳频序列一直是扩频通信领域的基础理论研究课题.跳频序列理论包括理论界与序列设计2个方面.长期以来,跳频序列的研究成果很丰富,但部分跳频序列的研究结果不多.本文系统地阐述部分汉明相关跳频序列(集)的研究成果. 表1中列出了具有最优部分汉明相关的跳频序列(集)的参数. 表 1 具有最优部分汉明相关的跳频序列(集) r>1是整数,且r|gcd(e,q1-1,q2-1,…,qt-1); d和n是正整数,p是一素数,ξ和ξ′是一素数幂;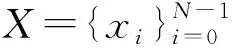
3 部分汉明相关理论界
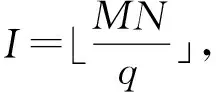
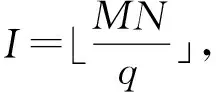
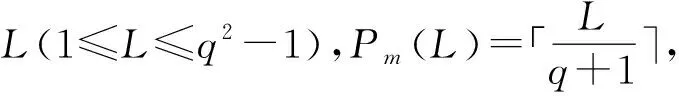
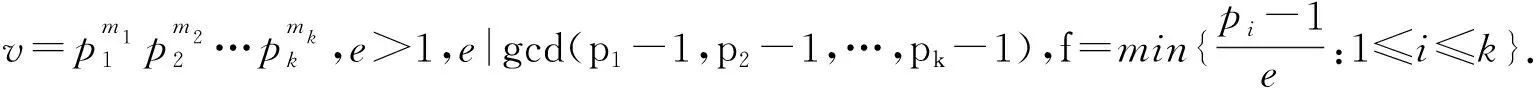
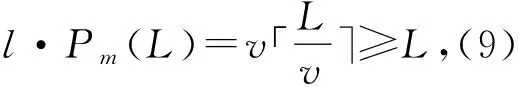
4 基于广义m序列和广义GMW序列的严格最优跳频序列集
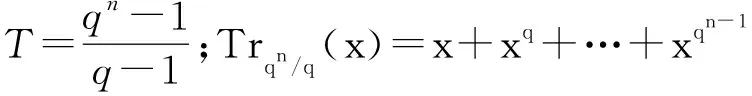
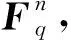
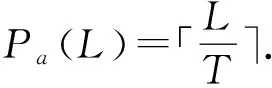
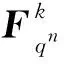
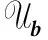
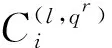
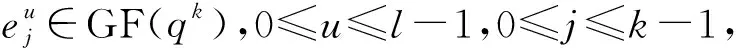
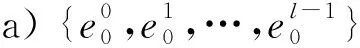
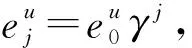
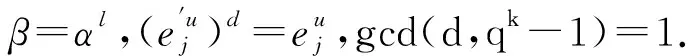
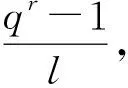
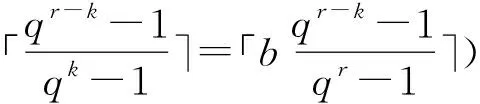
5 基于广义分圆的强最优部分汉明相关跳频序列(集)
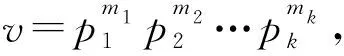
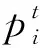


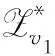
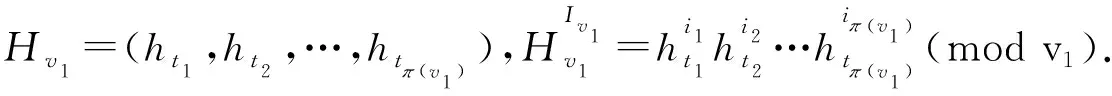
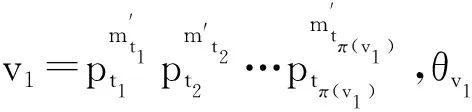
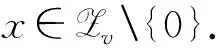
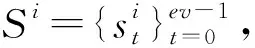
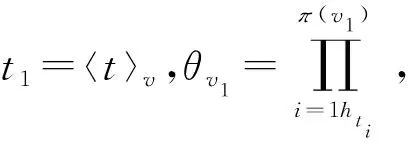
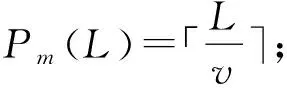
6 具有最优序列集大小的强最优部分汉明相关跳频序列集设计
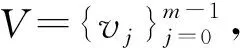
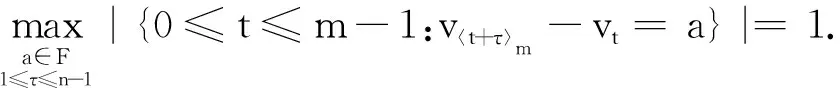
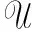
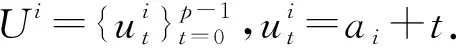
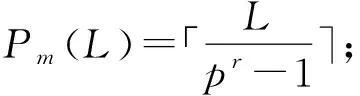
7 基于不相交循环完美Mendelsohn差族的强最优跳频序列设计

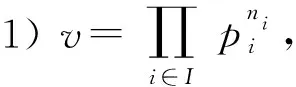
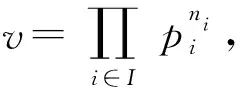
8 基于多重可划分平衡嵌套循环差填充的强最优跳频序列集设计
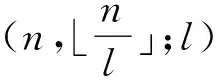

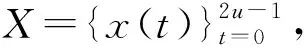
9 基于可划分差填充的强最优跳频序列集设计
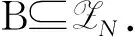
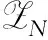
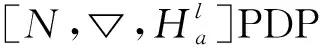
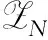
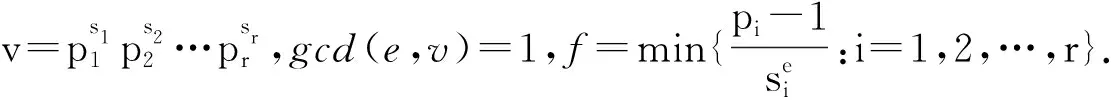
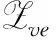

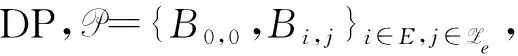
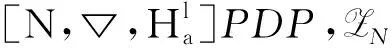
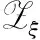
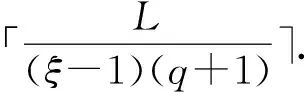
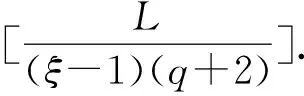
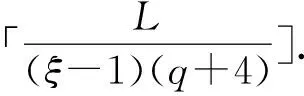


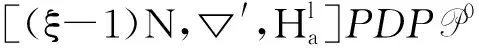
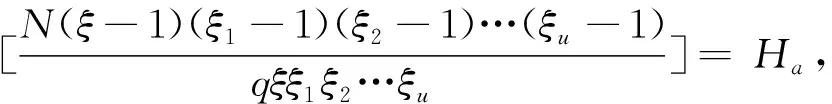
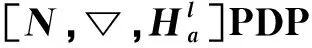
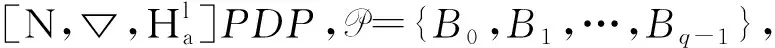
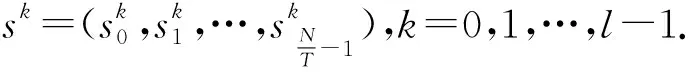
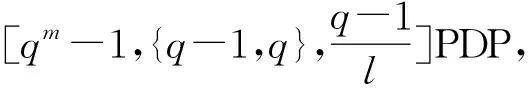
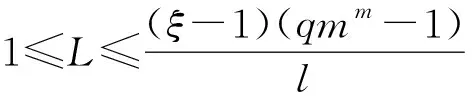
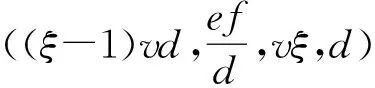
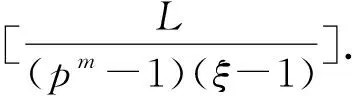
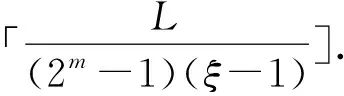
10 结束语