丰富表象储备 培养数学思维

江苏省南京市西善花苑小学 蔡 琦

一、表象储备概述

表象是指客观对象不在主体面前呈现时，在脑海中所保持的客观对象的形象和客体形象在观念中复现的过程。表象不仅是一个人的印象，而且是一种操作，即心理操作可以以表象的方式进行，也就是形象思维活动。从生理学来说，表象储备属于一种由感官加工过的信息，它是当下进行的，只有对外物进行刺激且由感官转化得到的信息才是表象的物理状态，当外物刺激消失时，它就会转变为储存的信息。

二、拓展感知渠道，丰富表象储备

（一）数形结合，构造表象

在低年级的数学教学中，有关数的教学对刚刚迈入小学的低年级学生来说是比较抽象的。学生可能在幼儿园的时候就已经知道数、会写数、会数数，但是大部分学生没有真正理解数的意义。因此，在数的教学过程中，教师需要遵循低年级学生的思维特点和心理特征，结合学生的生活经验，借助具体直观的模型，通过多种途径丰富学生的表象储备，给予学生认识数、理解数的意义一个直观的支撑。

例如，在教学苏教版数学一年级上册“认识0~10各数”时，为了帮助学生认识数、理解数，教师可以借助圆片、小棒、计数器等直观模型（见图1），让学生经历数一数、摆一摆、拨一拨的过程，把数形结合的表象变成储存在脑海里的信息，把抽象的数变得具体、鲜活，为培养学生的思维能力奠定基础。

图1

在高年级数的教学过程中同样存在借助表象进行理解的需要。例如，在教学苏教版数学五年级上册“认识负数”时，由于大部分学生在之前的学习中从未接触过负数，对于负数了解仅仅停留在会读、会写的层面。因此，在教学过程中，教师可以引导学生自主表达对负数的理解，可以画实物图，可以是生活化的场景，如电梯按键上的负一楼、气温中的零下几摄氏度，甚至可以是计算结果的呈现。接下来，教师通过整理学生提供的实物图以及运算解答等多维度的表达方式，帮助学生构建了多方面、多角度的表象材料，不仅促进了学生对负数的认知，也为学生思维的发展提供了丰富的表象储备。

（二）多感官参与，丰富表象

在数学学习中，所有的表象都不能缺乏感知。因此，在数学教学中，教师要帮助学生树立良好的感知。小学生的实际感知能力通常来说处于感知初级阶段，教师要通过多种多样的实物材料来丰富学生的表象储备，进一步提高学生的感知能力，从而达到一定的感知效果。

例如，在教学苏教版数学六年级上册“长方体和正方体的认识”一课时，教师可以让学生提前准备日常生活中常见的小纸箱、牙膏盒、魔方等物体。首先，引导学生通过摸一摸，明确哪些是长方体的物体，哪些是正方体的物体，唤醒学生对不同图形的认知，帮助学生快速地形成长方体和正方体的表象积累；其次，引导学生通过说一说长方体和正方体的特征，帮助学生总结长方体和正方体的特征，逐步形成对长方体和正方体关键特征的认知；最后，引导学生不断对比图形来调整脑海中的图形形象（见图2）。在这样触觉、听觉、视觉等多感官的参与中，学生增加了对长方体和正方体不同特征的表象储备，对长方体和正方体的特征也形成了比较牢固的感知。

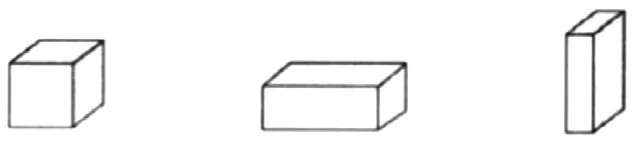
图2

三、强化表象储备，提升数学思维

数学新课标中明确指出：在数学课堂教学活动中，要以激发学生学习兴趣、提高学生学习的积极性、调动学生对数学问题的思考、鼓励学生的数学创造性思维为目的。

（一）以类比与联想教育为桥梁，重建表象储备

培养学生的思维能力是数学教学的重要内容之一，对学生的思维能力进行全面培养是推动现代教学应用的必要手段。学生的思维能否有创造性的发展，主要取决于其头脑中所存在的表象储备的重新构建与改造，类比和联想的思维方法便能支撑这些表象的重新构建与改造，让在场和不在场的互相沟通与关联，构成思维发展的空间。

例如，在教学苏教版数学六年级下册“圆柱的体积”一课时，圆与圆柱便是能够沟通和关联的数学表象。在学习圆柱之前，学生已经学习过圆的面积，圆的面积推导便是学生已有的表象储备，作为与圆柱紧密相连的表象储备，在实际教学中，教师可以有意识地引导学生把圆和圆柱进行类比，学生便可以由圆的面积推导想到圆柱体积的推导（见图3）。

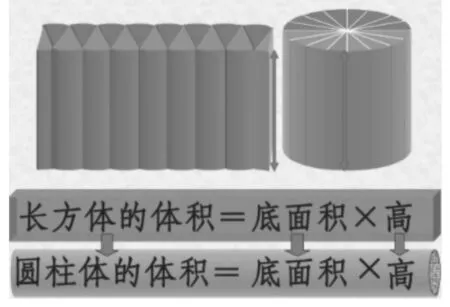
图3

而类比的进阶便是联想，它是一种发散性思维。学会联想有利于在解决新问题时进行发散性的思考，提供多种创造性解决问题的路径，促进问题的解决。

例如，在教学苏教版数学五年级上册“小数乘整数”一课时，教材提供给学生的是卖西瓜的真实生活情境，情境图出示夏天西瓜0.8元/千克，买3千克西瓜需要多少钱？结合自身的实际，不同的学生会有不同的表象储备，因此也会产生不同的思维触发，学生可能会呈现出不同的联想：（1）通过0.8×3这个乘法算式，学生可以联想到乘法的意义这一表象储备，得到加法算式0.8+0.8+0.8=2.4（元），从而利用加法解决乘法问题；（2）学生可能想到3个0.8合起来是24个0.1，也可以得出0.8×3=2.4的结论；（3）学生也可能通过0.8元联想到8角，便将这个小数乘整数的问题转化成整数乘法，0.8元=8角，8×3=24（角），24角=2.4元，从而解决问题。

不同的学生基于提供的数学信息和自身已有的表象储备会产生不同的联想，建立不同的联系。建立了不同的联系，学生就会有不同的表象储备加工和重组的方式，因此也会产生多样的解决问题的方法。正是这些不同才能使学生的思维在课堂上相互碰撞、开枝散叶，使数学课堂更加具有生命力。

（二）多种方式建立完善的表象，培养学生思维能力

在数学教学中，教师需要在学生初步建立表象的过程中对学生进行思维引导，帮助学生在丰富表象储备的同时提升自身的思维能力。如在数学概念课的教学中，由于数学概念对学生来说也是比较抽象的，针对学生的认识能力和心理特征，开展教学问题设计是很有必要的。教师精心设计不同的教学问题的目的主要是强化学生的表象储备，从而提升学生的思维能力。教师要提出能够发散学生思维、充分调动学生学习积极性与主动性的数学问题，并通过多样化的问题和个性化的提问方式来促进更为全面的课堂应用。学生的思维能力只有在思维活跃的时候，才能得到有效的提升。因此，教师要根据教学内容和学生的实际表象储备情况提出难度适中且具有思考性与发展性的问题，这样才能激活每个学生的思维，将被动的教学转化为主动的学习，提高学生的思维积极性和发散性。

教学手段的使用在一定程度上可以丰富并完善学生的表象，促进学生的数学形象思维。传统的教学模式给学生提供的直观表象毕竟有限，思维能力较弱的学生也许只能初步建立表象，这样传统单一的教学方式往往是流于形式，不有利于学生在头脑中产生直观的印象，忽略了课堂互动的积极性，不能真正地帮助学生完善表象、培养思维能力。随着科学技术的发展，越来越多的现代教学手段逐渐出现，并广泛应用在数学教学中。教师可以根据不同的教学内容，运用合适的教学手段，例如动画演示、动手操作演示、模型、展台、微课、翻转课堂等。这些先进而又丰富的教学手段弥补了传统教学手段的不足，拓展了教师直观教学的手段。教师在教学过程中运用直观的教学手段，可以在学生建立表象的基础上辅以生动形象的动画，也可以在学生操作的过程中不断提问、对比、交流，帮助学生获得生动而又具体的直观认识，完善建立的表象。同时给学生提供了思维碰撞的平台，真正发展了学生的思维能力。

综上所述，在数学教学中，通过多种教学手段对学生的思维能力进行培养和提升是目前数学教学的重难点。学生通过储备丰富清晰的表象材料，掌握类比、联想的思维技能；教师通过多种方式完善学生的表象，培养学生的思维能力。这样的数学课堂是真正从学生的认知特点和心理特征出发，丰富并完善学生的表象储备，对学生开展有针对性的思维能力培养，加强教学过程中的师生互动，提高学生学习的主动性与感知能力，并促进学生形象思维、逻辑思维和创造能力的发展，使学生的“思维之树”在课堂中开枝散叶。