完全AC分解

侯婷婷, 杨晓燕

(西北师范大学 数学与统计学院, 兰州 730070)

1 预备知识

若无特殊说明, 本文所有的环R均为结合环, 所有的R-模均为左R-模.复形ΣsM定义为

则

M⊆n=0→Cn(M)→Mn-1→Mn-2→….

对

supM=sup{n∈|Hn(M)≠0},

如果M正合, 则记supM=-∞.设M,N是复形,

dM⊗RN(x⊗y)=dM(x)⊗y+(-1)|x|x⊗dN(y).

如果对任意的n∈,Hn(f):Hn(M)→Hn(N)是同构, 则称f:M→N是复形同态间的拟同构.令f:M→N是复形同态, 映射锥复形cone(f)定义为

如果A⊥1=B, A=⊥1B, 则称(A,B)是左R-模中的余挠对, 其中

定义1[4,7]令(A,B)是左R-模中的余挠对,X是链复形.

1) 如果X正合, 且对任意的n,Zn(X)∈A, 则称X是A复形;

2) 如果X正合, 且对任意的n,Zn(X)∈B, 则称X是B复形;

3) 如果对任意的n,Xn∈A, 且对任意B复形B有HomR(X,B)正合, 则称X是dg-A复形;

4) 如果对任意的n,Xn∈B, 且对任意A复形A有HomR(A,X)正合, 则称X是dg-B复形.

定义3[9]1) 如果存在左R-模的正合列

…→P1→P0→F→0,

则称左R-模F是FP∞的, 其中Pi是有限生成投射模;

定义4[6]如果存在一个平坦模的正合列

F=…→F1→F0→F-1→F-2→…,

使得:

1)M≅Ker(F0→F-1);

2) 对任意绝对clean右R-模A,A⊗-作用上述正合列仍是正合的.

则称左R-模M是Gorenstein AC平坦模.

将Gorenstein AC平坦模类记为GFac.

注11) {平坦模}⊆{Gorenstein AC平坦模}⊆{Gorenstein平坦模}.

2) 由文献[9]中定理2.12知, 对于任意环R,N是level模当且仅当N+是绝对clean模,N是绝对clean模当且仅当N+是level模.由文献[9]中命题A.5知, 若C是链复形,M是右R-模, 则M⊗RC正合当且仅当HomR(C,M+)正合, 从而在上述Gorenstein AC平坦模的定义中, 对任意绝对clean右R-模A,A⊗-作用正合等价于对任意level左R-模L, HomR(-,L)正合.又因为所有的平坦模是level模, 所以对任意平坦左R-模F, HomR(-,F)正合, 从而可保证下面构造完全AC分解的可行性.

证明: 因为G1是Gorenstein AC平坦模, 所以由文献[6]中引理4.4知, 存在短正合列

0→G1→F→G2→0,

其中F是平坦模,G2是Gorenstein AC平坦模.考虑下列推出图:

从而有下列推出图:

在正合列

0→G0→G→G2→0

中,G0和G2是Gorenstein AC平坦模, 所以G是Gorenstein AC平坦模.由上述两个推出图可得

0→K→F→G→M→0

正合, 其中F是平坦模,G是Gorenstein AC平坦模.另一个正合序列可对偶地由拉回图得到.

2 主要结果

1)π是M的一个dg-平坦分解;

2)T是一个对任意的绝对clean右R-模A,A⊗-作用正合的平坦模的正合列, 且对任意的i∈,Zi(T)是Gorenstein AC平坦模;

3)τ:T→F是一个态射, 使得对任意的i≫0时, 有τi=idTi.

如果对任意的i∈,τi是可裂满态射, 则称M的一个完全AC分解是可裂的.

定义6令R是环,M是复形.M的Gorenstein AC平坦维数记为GFac-dimM, 定义为

GFac-dimM=inf{sup {l∈

若M正合, 则记GFac-dimM=-∞, 若不存在满足上述条件的n, 则记GFac-dimM=∞.

定理1令R是环,M是复形,n是整数, 则下列结论等价:

1) GFac-dimM≤n;

3) supM≤n, 且对任意的F≃M有Cn(F)∈GFac, 其中F是dg-平坦复形;

3)⟹4).由3)知supM≤n, 且存在一个dg-平坦复形F≃M, 使得Cn(F)∈GFac.由文献[6]中引理4.4可得A⊗-作用正合的正合列

0→Cn(F)→Tn-1→Tn-2→…,

其中Ti是平坦模,A是任意的绝对clean右R-模.令

T′=…→Fn+1→Fn→Tn-1→Tn-2→…,

且T′是正合的.又

cone1F≤n-1=0→Fn-1→Fn-1⊕Fn-2→Fn-2⊕Fn-3→…,

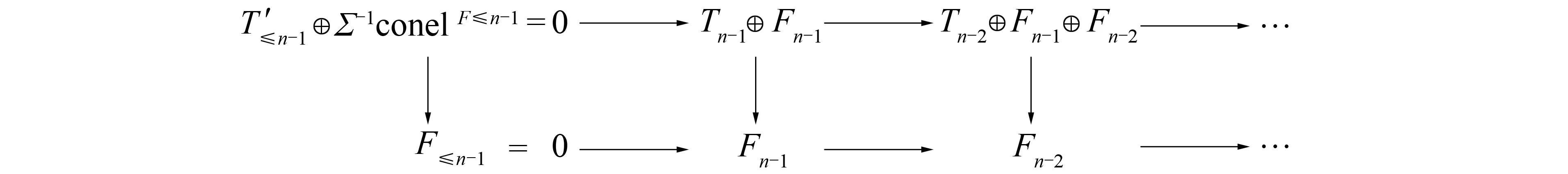
令

4)⟹5)显然成立.

推论1令R是环,M是复形.则GFac-dimM≤fdRM成立, 且当fdRM<∞时等号成立.

证明: 如果fdRM=∞, 则不等式显然成立.若M正合, 则结论显然成立.下面假设M不正合,fdRM=n<∞, GFac-dimM=m, 则由定理1可得m≤n.下证m=n.用反证法, 设m

0→Cn(F)→Fn-1→…→Fm→Cm(F)→0,

且当n>i≥m时有Ci(F)∈GFac, 于是Cn-1(F)∈GFac, 且

0→Cn(F)→Fn-1→Cn-1(F)→0

是正合列.因为fdRM=n, 所以Cn(F)是平坦模, 从而Cn-1(F)有有限的平坦维数.又因为Gorenstein AC平坦模是Gorenstein平坦模, 所以Cn-1(F)是有有限平坦维数的Gorenstein平坦模, 从而由文献[11]知Cn-1(F)是平坦模.故

F⊆n-1=0→Cn-1(F)→Fn-2→…

是平坦模的序列.因为F≅M, 所以F⊆n-1≃M, 且存在复形的短正合列

0→F′→F→F⊆n-1→0.

又因为F⊆n-1是平坦模的序列, 所以上述复形短正合列是层次纯正合的.由文献[12]中命题6.2知,F⊆n-1是dg-平坦复形, 因此fdRM≤n-1.矛盾.故m=n, 从而GFac-dimM≤fdRM.

注2M的Gorenstein AC平坦维数也可定义为

GFac-dimM=inf{n∈是M的完全AC分解, 使得对i≥n有τi是双射}.

0→M→C→L→0,

0→K→F′→C→0,

进而F→M是M的dg-平坦分解.因为GFac-dimM≤n, 所以由定理1可得Cn(F)∈GFac.由文献[6]中引理4.4知, 存在A⊗-作用正合的正合列

因此T′是A⊗-作用正合的正合列, 其中A是任意的绝对clean右R-模.则可得如下拉回图: