5类图的优美性
唐保祥, 任 韩
(1.天水师范学院 数学与统计学院, 甘肃 天水 741001; 2.华东师范大学 数学科学学院, 上海 200062)
1 引言与预备知识
优美图在晶体结构中的原子位置测定、物流运输、编码设计、通讯网络、X射线密码技术、天文学、导弹控制、雷达和数据库管理等领域应用广泛[1-2].但目前对一般图的优美性研究尚无系统性理论.研究表明, 判定任意一个图是否为优美图是一个NP难问题.目前, 对图优美性的证明一般仍用构造性方法[3-17].
最省刻度尺问题为: 设m,n为正整数, 在长为n(任意一个确定的值)厘米的无刻度尺上添加m个刻度(包括直尺两端的刻度), 使其可以度量1~n内任何整厘米长度的尺寸, 求m的值至少是多少.该问题的一般情形目前尚未解决[17].
定义1[1]设图G=(V,E), 若存在单射θ:V(G)→{0,1,2,…,|E(G)|}, 使得∀e=uv∈E(G), 由θ′(e)=|θ(u)-θ(v)|可导出双射θ′:E(G)→{1,2,…,|E(G)|}, 则称图G是优美图,θ称为图G的一个优美标号,θ′称为由θ导出的边标号.
定义2[12-13]给定边数的优美图中顶点数最少的优美图称为极小优美图.
把完全二部图K2,n的顶点w与全图K3的顶点u0连接一条边, 再把K2,n的顶点v0与K3的顶点u0,u1,u2分别连接一条边得到的图记作K2,n-1-3-K3, 如图1所示.把完全二部图K2,n的顶点w与全图K3的顶点u0,u1分别连接一条边, 再把K2,n的顶点v0与K3的顶点u0,u1分别连接一条边得到的图记作K2,n-2-2-K3, 如图2所示.

图1 图K2,n-1-3-K3Fig.1 Graph K2,n-1-3-K3
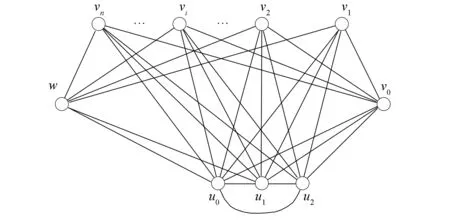
图2 图K2,n-2-2-K3Fig.2 Graph K2,n-2-2-K3
把完全二部图K2,n的顶点w与全图K3的顶点u0连接一条边, 再把K2,n的顶点v0与K3的顶点u0,u1分别连接一条边得到的图记作K2,n-1-2-K3, 如图3所示.把完全二部图K1,n的顶点v0与K3的顶点u0,u1分别连接一条边得到的图记作K1,n-2-K3, 如图4所示.把完全二部图K1,n的顶点v0与有3个顶点的路P3的顶点u1,u0,u2分别连接一条边得到的图记作K1,n-3-P3, 如图5所示.

图3 图K2,n-1-2-K3Fig.3 Graph K2,n-1-2-K3

图4 图K1,n-2-K3Fig.4 Graph K1,n-2-K3
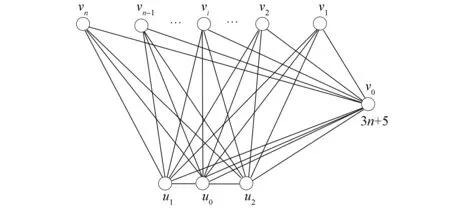
图5 图K1,n-3-P3Fig.5 Graph K1,n-3-P3
n个整数单位长度的直尺, 最少添加m个刻度(这m个刻度包括尺子的两个端点), 使得能度量1~n内任何整数单位长度的尺寸, 这样的直尺度量方式, 对应一个图: 有m个顶点、n条边的图, 任意一对顶点的两个数值较大数与较小数之差恰好是1,2,…,n.此时该图形为一个极小优美图.
本文证明5类结构相似但不同构的图是优美图.当1≤n≤5时, 图K2,n-1-3-K3,K2,n-2-2-K3,K2,n-1-2-K3和K1,n-3-P3都是极小优美图.因此, 每个n值对应图的顶点标号, 均可给出对应尺长(图的边数)的最省刻度.图K2,n-1-3-K3,K2,n-1-2-K3和K1,n-3-P3中n=1~5, 得到15组对应尺长最省刻度的数值.
2 主要结果

图6 图K2,n-1-3-K3的优美标号Fig.6 Graceful labeling of graph K2,n-1-3-K3
定理1∀n∈+, 图K2,n-1-3-K3是优美图.
证明: 设图K2,n-1-3-K3的顶点集合为{u0,u1,u2,w,vi|i=0,1,2,…,n}, 由图K2,n-1-3-K3的定义知
|E(K2,n-1-3-K3)|=5n+7,
|V(K2,n-1-3-K3)|=n+5.
定义图K2,n-1-3-K3顶点的标号θ1如下:
θ1(u0)=0,θ1(u1)=n+1,
θ1(u2)=2n+3,θ1(w)=3n+5;
θ1(vi)=4n+7+i,i=0,1,2,…,n.
图K2,n-1-3-K3的标号θ1如图6所示.根据标号θ1的定义, 图K2,n-1-3-K3的集合为{u0,u1,u2,w,vi|i=0,1,2,…,n}, 定义的标号集合为{0,n+1,2n+3,4n+7+i|i=0,1,2,…,n}.所以映射θ1:V(K2,n-1-3-K3)→{0,1,2,…,5n+7}是单射.
映射θ1导出的边标号如下:

定理2∀n∈+, 图K2,n-2-2-K3是优美图.
证明: 设图K2,n-2-2-K3的顶点集合为{u0,u1,u2,w,vi|i=0,1,2,…,n}, 由图K2,n-2-2-K3的定义知,
|E(K2,n-2-2-K3)|=5n+7,
|V(K2,n-2-2-K3)|=n+5.
定义图K2,n-1-2-K3顶点的标号θ3如下:
θ2(u0)=0,θ2(u1)=n+1,θ2(u2)=2n+3,θ2(w)=3n+5;
θ2(vi)=4n+7+i,i=0,1,2,…,n.
图K2,n-2-2-K3的标号θ2如图7所示.
类似定理1的证明易知,θ2是图K2,n-2-2-K3的一个优美标号, 因此图K2,n-2-2-K3是优美图.
定理3∀n∈+, 图K2,n-1-2-K3是优美图.
证明: 设图K2,n-1-2-K3的顶点集合为{u0,u1,u2,w,vi|i=0,1,2,…,n}, 由图K2,n-1-2-K3的定义知
|E(K2,n-1-2-K3)|=5n+6,
|V(K2,n-1-2-K3)|=n+5.
定义图K2,n-1-2-K3顶点的标号θ3如下:
θ3(u0)=0,θ3(u1)=n+1,θ3(u2)=2n+3,θ3(w)=3n+4;
θ3(vi)=4n+6+i,i=0,1,2,…,n.
图K2,n-1-2-K3的标号θ3如图8所示.

图7 图K2,n-2-2-K3的优美标号Fig.7 Graceful labeling of graph K2,n-2-2-K3

图8 图K2,n-1-2-K3的优美标号Fig.8 Graceful labeling of graph K2,n-1-2-K3
类似定理1的证明易知,θ3是图K2,n-1-2-K3的一个优美标号, 所以图K2,n-1-2-K3是优美图.
定理4∀n∈+, 图K1,n-2-K3是优美图.
证明: 设图K1,n-2-K3的顶点集合为{u0,u1,u2,vi|i=0,1,2,…,n}, 由图K1,n-2-K3的定义知,
|E(K1,n-2-K3)|=4n+5,
|V(K1,n-2-K3)|=n+4.
定义图K1,n-2-K3顶点的标号θ4如下:
θ4(u0)=0,θ4(u1)=n+1,θ4(u2)=2n+3;
θ4(vi)=4n+5+i,i=0,1,2,…,n.
图K1,n-2-K3的标号θ4如图9所示.
类似定理1的证明易知,θ4是图K1,n-2-K3的一个优美标号, 所以图K1,n-2-K3是优美图.
定理5∀n∈+, 图K1,n-3-P3是优美图.
证明: 设图K1,n-3-P3的顶点集合为{u0,u1,u2,vi|i=0,1,2,…,n}, 由图K1,n-3-P3的定义知,
|E(K1,n-3-P3)|=4n+5,
|V(K1,n-2-K3)|=n+4.
定义图K1,n-3-P3顶点的标号θ5如下:
θ5(u0)=0,θ5(u1)=n+1,θ5(u2)=2n+3;
θ5(vi)=3n+5+i,i=0,1,2,…,n.
图K1,n-3-P3的标号θ5如图10所示.

图9 图K1,n-2-K3的优美标号Fig.9 Graceful labeling of graph K1,n-2-K3

图10 图K1,n-3-P3的优美标号Fig.10 Graceful labeling of graph K1,n-3-P3
类似定理1的证明易知,θ5是图K1,n-3-P3的一个优美标号, 所以图K1,n-3-P3是优美图.
3 应 用
文献[12]已经证明: 边数为m的极小优美图G的顶点数为f(m), 则
其中[x]表示大于等于x的最小整数.
根据上述结论, 当1≤n≤5时, 图K2,n-1-3-K3,K2,n-2-2-K3,K2,n-1-2-K3和K1,n-3-P3都是极小优美图.因此, 每个n值对应图的顶点标号, 都给出了对应尺长(图的边数)的最省刻度.图K2,n-1-3-K3,K2,n-1-2-K3和K1,n-3-P3中n=1~5, 对应尺长的最省刻度分别列于表1~表3.

表1 K2,n-1-3-K3的边数、顶点数及对应的最省直尺刻度值

表2 K2,n-1-2-K3的边数、顶点数及对应的最省直尺刻度值

表3 K2,n-3-P3的边数、顶点数及对应的最省直尺刻度值

