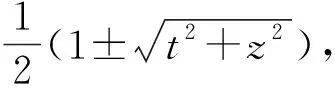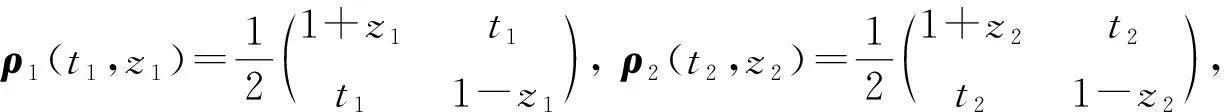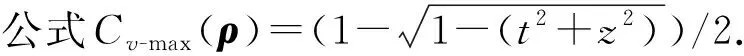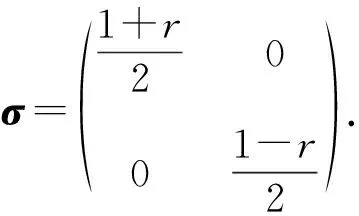单量子系统中基于相干度量的态排序

胡晓会, 玄东平, 南 华

(延边大学 理学院, 吉林 延吉 133002)

量子相干性在低温热力学、量子生物学和纳米物理学等领域应用广泛.文献[1]提出了量化相干资源理论框架；文献[2]提出了另一个量化相干框架.在量子信息处理进程中存在不同相干度量, 如l1-范数相干度量、相对熵相干度量和鲁棒相干度量等.与量子纠缠类似, 不同的量子相干度量可表征不同量子态, 一个给定的量子态可能在一次信息处理中表现较好, 但在其他信息处理中该量子态的适用性可能相对较差.若2个纠缠度量对纯态有相同排序, 则任意2个态就会有相同排序, 从而纯态中存在的排序关系即可延拓至任意的量子态[3].若2个相干度量对所有量子态有相同排序, 则可在某种程度上识别它们.由于不同的相干度量有不同排序, 因此在不同的量子相干度量下如何对量子态进行排序已引起人们广泛关注[4].

文献[5-7]研究了l1-范数相干度量、相对熵相干度量以及α亲和相干度量的量子态排序关系；文献[8]研究了Tsallis-α相对熵相干度量的量子态排序.本文基于相对熵相干度量、斜信息相干度量和Hellinger距离相干度量等研究单量子系统中的态排序.

1 几种相干度量和态排序

(1)

其中Dmax(ρ‖σ)=min{λ:ρ≤2λσ}是量子态ρ相对于量子态σ的最大相对熵.

定义1[6]设CA和CB是2个相干度量, 对于Hilbert空间H中任意2个态ρ1和ρ2, 若

CA(ρ1)≤CA(ρ2) ⟺CB(ρ1)≤CB(ρ2),

则称CA和CB提供相同的态排序.否则, 称这2个度量不能提供相同的态排序.

由于C(ρ)是一个非负实数, 因此根据不同相干度量, 所有的态总可以进行排序.

2 基于相干度量的纯态排序

根据不同相干度量研究纯态的单量子比特系统中态排序问题.

结论1对于单量子比特系统中的纯态, 相对熵相干度量Cr、斜信息相干度CI以及Hellinger距离相干度量CH提供相同的态排序.

证明： 单量子系统中任意量子态设为

(2)

(3)

以及Hellinger距离相干度量

(4)

由式(3)和式(4)可知,CI(ρ)和CH(ρ)均为关于|b|的增函数, 因此相干度量CI(ρ)和CH(ρ)具有相同的态排序.即对任意2个纯态ρ1和ρ2, 有CI(ρ1)≤CI(ρ2)⟺|b1|≤|b2|⟺CH(ρ1)≤CH(ρ2).

任意的单量子比特态ρ通常还可表示为

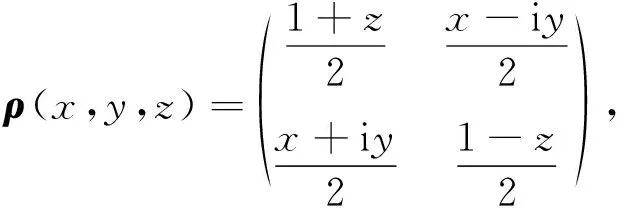
(5)

其中x2+y2+z2≤1(纯态时等号成立).令

(6)

例1考虑如下2个单量子比特纯态:

通过计算可得

Cr(σ1)=0.721 9

CH(σ1)=0.350 8

从而验证了上述相干度量提供相同的态排序.

例2考虑如下2个单量子比特混合态:

由定义可得

Cr(σ1)=0.627 1>Cr(σ2)=0.533 8,CI(σ1)=0.241 0>CI(σ2)=0.201 2,

CH(σ1)=0.257 6>CH(σ2)=0.212 5.

3 基于相干度量的混合态排序

下面讨论混合态Cr,CI,CH的态排序问题.根据CI(ρ)和CH(ρ)的定义解析表达式可知, 由于CI(ρ)和CH(ρ)对任意态提供相同的态排序, 因此仅需讨论Cr(ρ)和CI(ρ)的态排序,Cr(ρ)和CH(ρ)必有类似的结果.

图1 当时, ΔCI的三维图像Fig.1 Three-dimensional image of ΔCI when t1=4/5,

(7)

结论2对单量子比特系统中的混合态,Cr和CI及Cr和CH不能提供相同的态排序.

例3对单量子系统中的2个量子态:

可直接计算求得基于不同度量的相干性：

CI(σ1)=0.32>CI(σ2)=0.304 0,CH(σ1)=0.350 8>CH(σ2)=0.331 5,

Cr(σ1)=0.721 9

例2中Cr(ρ)和CI(ρ)及Cr(ρ)和CH(ρ)同序, 但在这里是反序, 因此Cr和CI及Cr和CH不能提供相同的态排序.

结论3对单量子比特系统中的混合态,Cv-max(ρ)和Cr(ρ),Cv-max(ρ)和CI(ρ)及Cv-max(ρ)和CH(ρ)均不能提供相同的态排序.

例4对如下3个混合态:

Cv-max(σ1)=0.334 9>Cv-max(σ2)=0.201 2

(8)

CI(σ1)=0.241 0>CI(σ2)=0.201 2

(9)

Cr(σ1)=0.627 1>Cr(σ2)=0.533 8

(10)

式(8)～(10)中至少有一个不等号方向不一致, 表明Cv-max(ρ)和Cr(ρ),Cv-max(ρ)和CI(ρ)及Cv-max(ρ)和CH(ρ)均不能提供相同的态排序.

结论4对单量子比特系统态(纯态或混合态), 最大相对熵相干度量Cmax(ρ)与l1-范数相干度Cl1提供相同的态排序.

由此可得Cmax(ρ)与其他相干度量的态排序关系.

综上, 本文研究了在单量子比特系统中基于几个相干度量的态排序问题, 并讨论了Cv-max(ρ)以及Cmax(ρ)与其他相干度量的态排序问题.结果表明：l1-范数相干度量、相对熵相干度量、斜信息相干度量及Hellinger距离相干度量对纯态提供相同的态排序, 对混合态则不能提供相同的态排序, 并给出了例证; 基于von Neumann测量的最大相干度量、相对熵相干度量及斜信息相干度量对混合态也不能提供相同态排序.