中间特征向量灵敏度的自适应迭代计算

陈锦洪, 钟慧湘, 吴柏生

(广东工业大学 机电工程学院, 广州 510006)

在结构动力学模型校正、优化和损伤检测等领域, 均需用到特征值和特征向量的导数[1-3].其中, 特征值的导数计算较容易, 但特征向量的导数计算则较复杂, 这主要是由于特征向量导数控制方程的系数为奇异矩阵所致.目前, 关于特征值和特征向量导数的计算方法可分为精确解法和近似解法两类.精确解法主要有模态叠加法[4]、Nelson方法[5]和改进的Nelson方法[6]等.模态叠加法需已知整个结构所有振型信息才能准确计算特征值与特征向量的导数, 但不易获得工程结构的全部振型信息.Nelson方法和改进的Nelson方法直接改变系数矩阵的奇异性, 前者仅适合单特征值的特征向量导数计算, 后者可用于单和重特征值的特征向量导数计算.但这类方法在计算每个频率对应的特征向量导数时均需对系数矩阵进行换行换列, 且需分解新形成的矩阵, 在编程和实施上均较繁琐.Yang等[7]提出一种计算特征向量灵敏度的方法, 但未讨论重特征值的情况, 且引入的正则项破坏了原有系数矩阵的稀疏性.为计算特征向量导数, 人们以模态叠加法为基础, 发展了计算特征向量导数问题的近似解法: Wu等[8]将预处理共轭梯度法(PCG)应用到特征向量导数问题中; Li等[9]通过修改系数矩阵(不同于Nelson方法和改进的Nelson方法)并利用迭代法实现了中间特征向量导数的计算; Lin等[2]对特征值和特征向量导数的理论和工程应用进行了较全面的综述.

针对特征向量导数计算问题, 本文提出一种自适应迭代方法用于计算任意频段内特征向量的导数.先自适应计算参与模态叠加所需的中间特征对, 再通过迭代方法自适应计算所需频带的特征向量导数.本文方法仅需求解移位特征值时已完成的移位刚度矩阵分解, 无需任何其他矩阵分解.数值算例验证了所提方法的有效性.

1 中间特征值对应特征向量导数的计算

对无阻尼系统自由振动, 其特征问题满足如下方程：

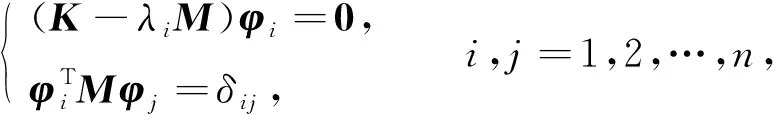
(1)

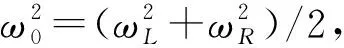
(2)

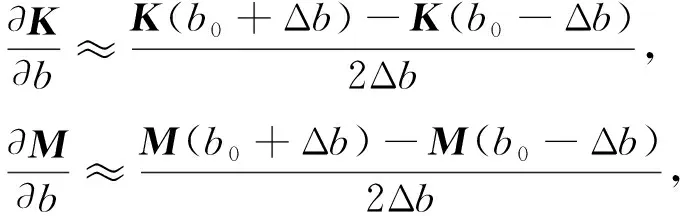
(3)

(4)

其中Δb为步长, 可通过文献[11]确定.

当m0>1时, 对应重特征值的情况.由于其重特征值对应的特征向量不唯一, 即φs+1,φs+2,…,φs+m0的任何线性组合仍是一个特征向量, 因此需找到可定义导数的特征向量.令λ0对应的特征向量矩阵为X=(φs+1,φs+2,…,φs+m0), 则重特征值的导数∂λi/∂b可通过求解

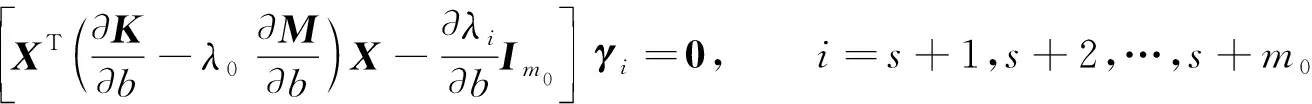
(5)

的特征值计算[12-13].假设所求重特征值的导数∂λi/∂b互不相同.设Γ=(γs+1,γs+2,…,γs+m0)为由方程(5)的特征向量构成的m0阶正交矩阵, 则可求导的重特征向量可表示为Z=XΓ.

设重特征向量导数的解为

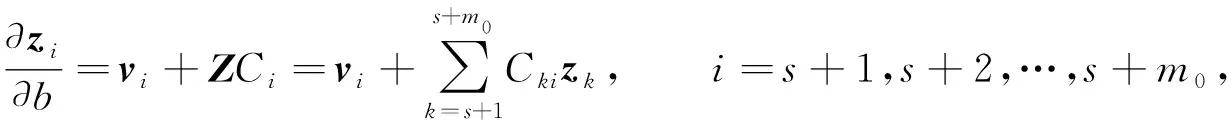
(6)

式中特解vi满足

(7)

当特解vi确定后, 系数Ci可由

(8)

求得.

文献[14-15]讨论了重特征值导数相同的情况, 本文只研究重特征值导数互不相同的情况, 其中m0=1对应单特征值, 其结果可简化.

2 中间特征向量导数的自适应迭代计算

由式(7)可知,K-λ0M是秩为n-m0的n阶矩阵, 其核空间由Z=(zs+1,zs+2,…,zs+m0)组成.基于Fox等[4]的模态叠加法, 特解vi(i=s+1,s+2,…,s+m0)可由所有除重频外对应的n-m0特征向量叠加求得, 即

(10)

其中

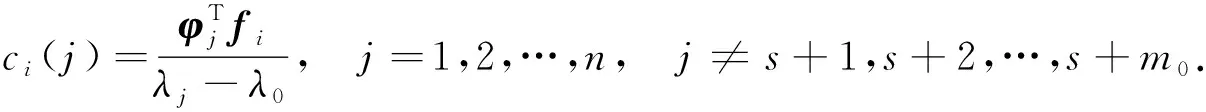
(11)

将方程(10)改写为

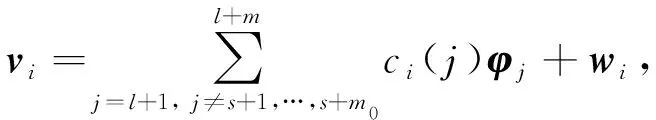
(12)

其中

(13)

模态叠加法需知道全部的模态信息, 但对大规模有限元模型, 不易求解全部模态.所以仅能对特解的一部分, 即中间特征向量Φm中对应的部分实施模态叠加；其补偿部分wi用

(14)

求解.由于K-λ0M为奇异矩阵, 因此文献[9]将式(14)修改为

(15)

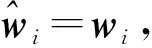
文献[9]给出了迭代式

wi,k+1=Gwi,k+f,k=0,1,2,…,

(16)

其中

(17)

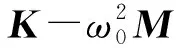
迭代矩阵G的谱半径

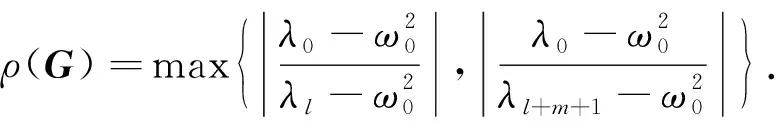
(18)

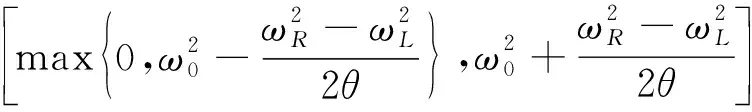
(19)

内, 这些中间特征对确定后, 由谱半径公式(18)可知, 在频带[ωL,ωR]内的特征对, 迭代矩阵的谱半径小于θ.

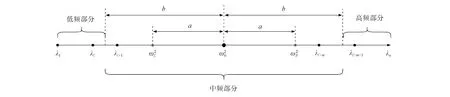
图1 特征值分布Fig.1 Eigenvalue distribution

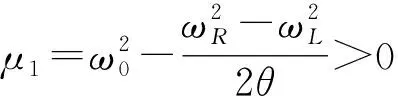
由式(16), 定义wi,k在第k次迭代后的残量相对于右端项fi的相对残差为

(20)

其中‖‖2为2-范数, 并取wi,0=0.定义容许误差ε, 当ri,k<ε时, 迭代解wi,k满足收敛精度要求.

基于上述讨论, 求解指定频带内重特征向量导数(单特征值的情形同样适用)的步骤如下：

1) 设定θ, 0<θ<1, 先计算由式(19)确定区间内的特征对Λm和Φm;

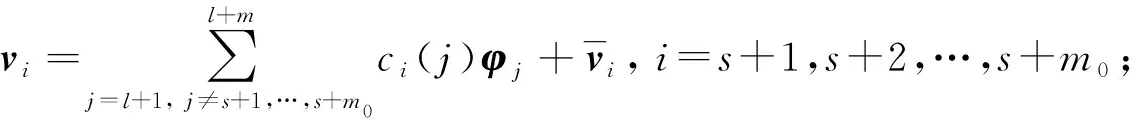
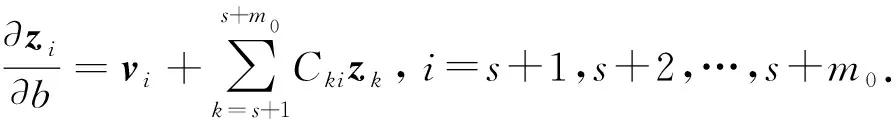
3 数值实验

下面通过数值算例验证本文方法的有效性.本文数值算例在配置如下的计算机上运行： 处理器为Intel(R) Xeon(R) Gold 6226R CPU@2.90 GHz 2.89 GHz(2处理器), 内存为256 GB, 系统为64位Windows 10.本文方法与改进Nelson方法的编程均采用软件MATLAB R2021a实现.采用MALTAB的eigs函数(采用默认收敛容差)求解移位特征值.相关的刚度矩阵和质量矩阵信息由ABAQUS建模获得.

本文方法比改进Nelson方法的优势通过CPU计算时间衡量, 自适应迭代方法的计算精度采用相对误差公式衡量.定义两特征向量导数的相对误差

考虑如图2所示的一个四边固定矩形板的固有振动问题.其长度x=2 m, 宽度y=2 m, 板厚h=0.01 m.材料的弹性模量E=78 GPa, Poisson比μ=0.32, 材料密度ρ=2 770 kg/m3.将该板划分成1 600个单元, 单元类型为Shell单元S8R5, 含31 205个自由度.以图3单元(黑色单元)的厚度为设计变量b, 其初始值b0=0.01 m, 步长Δb=0.000 1 m.假设频带为[260 Hz,320 Hz], 容许误差ε=10-4.

图2 矩形板结构Fig.2 Rectangular plate structure

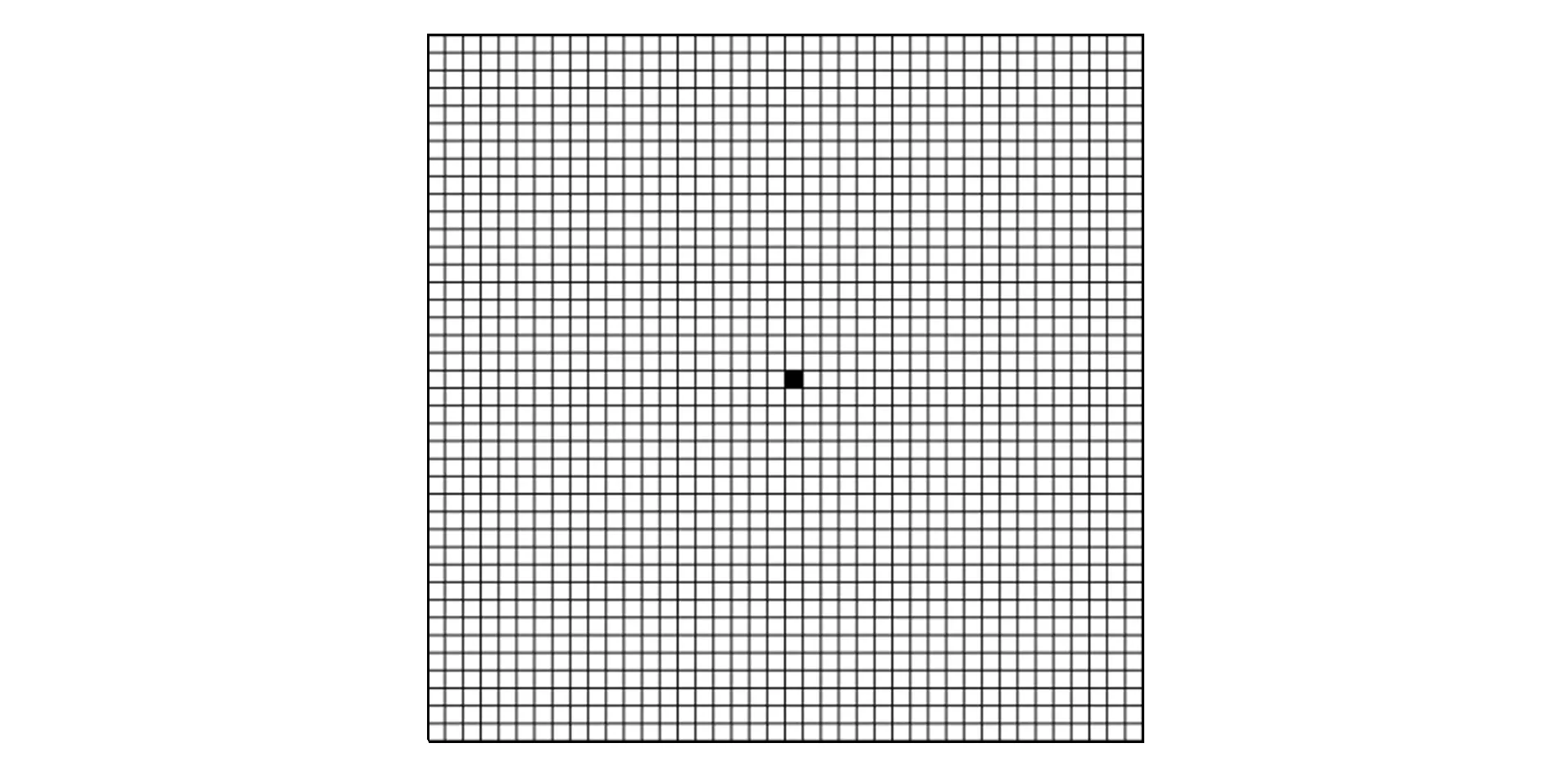
图3 板结构设计变量Fig.3 Design variables of plate structure

设θ=0.5.求解在区间[224.05 Hz,346.12 Hz]内的特征对Λm和Φm.通过Sturm定理求得该区间特征对的个数为11.采用本文方法计算关注频带内频率的导数列于表1, 采用本文方法与改进Nelson方法求解特征向量导数的相对误差列于表2.

表1 矩形板的频率及关注频带内频率的导数

表2 关注频带的特征向量导数的相对误差

由表2可见, 最大相对误差小于0.624%.计算关注频带的特征向量导数的总CPU时间, 采用本文方法需81.6 s, 采用改进Nelson方法需104.2 s, 总时间约缩减了22%.

综上所述, 针对特征向量导数计算问题, 本文提出了一种自适应迭代方法用于计算中间任意频带内的特征向量导数.通过设定θ值(小于1), 自适应计算参与模态叠加所需的中间特征对, 再通过迭代算法自适应求得关注频带内的特征向量导数.本文方法仅需在求解移位特征值时分解一次移位刚度矩阵, 无需任何其他矩阵分解.数值算例验证了本文方法的有效性.