基于对比学习方法的小样本学习

付海涛, 刘 烁, 冯宇轩, 朱 丽, 张竞吉, 关 路

(1.吉林农业大学 信息技术学院, 长春 130118；2.长春理工大学 经济管理学院, 长春 130022)

当前深度学习的应用大多数需要使用大规模的有标注数据进行监督学习, 而实际中制作精确标注且样本均衡的数据集需要大量的人力成本, 且在很多应用领域中数据的获取和标注可能还会遇到隐私和安全等方面的困难[1].实际应用中很多数据在分布上存在长尾分布的特征, 即数据种类与数量分布不均衡, 某些种类的数据量非常充足, 而另外一些种类的数据量较少, 导致相同模型在数据分布的两端表现不同[2].目前, 解决样本数据不足或不均衡问题的方法有许多, 如自监督学习、对比学习、元学习、小样本学习等, 其中小样本学习是研究在样本数量较少时, 如何既能学习利用分类特征又防止过拟合, 使机器学习系统能像人一样可通过少量样本的学习获得较鲁棒的判别能力[3].

数据增强是包括小样本学习在内很多技术都会采用的辅助方法, 其利用算法处理数据上采样训练集从而改进网络训练, 以解决样本缺乏或不均衡问题[4].利用数据自适应增强方法设计网络求解模型, 通过噪声、剪切、形变等方法增加新的数据用于训练, 但由于增强的数据与原数据具有特征的相似性, 本质上是一种人类知识的注入, 所以并未从根本上解决样本匮乏导致的过拟合问题[5]；基于迁移学习解决小样本学习问题, 先用充足的数据去训练原问题的模型, 再利用目标域中的少量数据进行模型微调[6]; 此外, 还有从特征角度进行迁移的方法, 如利用高级编码器提取特征并应用到小样本目标域中[7], 这类方法可提高模型的泛化能力, 但模型极易遗忘经验信息并依然会面临过拟合问题；结合元学习方法进行小样本学习, 该类方法利用任务或数据之间的共性使模型从少量样本中进行算法学习, 并能快速获得解决新任务的能力[8].为给模型找到更好的初始化, 可采用对参数进行梯度调整再训练的方法[9], 这类方法的分类效果显著, 但其过于复杂的网络结构会降低模型效率, 模型训练通常需要大量时间.

为改进小样本学习的求解, 结合深度学习方法的特点, 本文设计一种基于对比学习的小样本网络(contrastive networks for few-shot learning, CNFS)模型.针对小样本数据量少且分布不均衡的特点, 模型整体结构上采用对比学习方法, 网络的主体结构使用类孪生网络结构[10]；进行对比学习前, 模型首先用数据增强方法并且在特征提取部分的网络中采用经典的深度卷积网络作为骨干网络, 增加了重叠池化结构以加强特征提取[11]；在特征提取网络后, 使用分类网络学习样本之间的距离；针对对比学习模型训练时收敛慢和模型易过拟合的问题, 参考元学习方法的思想设计网络训练算法, 用嵌套循环在单组数据和小批量数据的规模上交替更新网络参数[9], 使网络能快速学习小样本特征并不影响整体的收敛趋势, 从而较快完成C-wayK-shot(C类,K样本)的小样本学习, 在每轮训练后都把正样本的特征向量拉近, 把负样本的特征向量拉远, 且不影响整体的收敛性.实验结果表明, 该网络在训练效率和准确率上都有提高.

1 预备知识

1.1 小样本学习

小样本学习是一种致力于通过少量样本, 甚至一个样本的训练使系统获得新分类能力的深度学习方法, 即在少量样本的基础上解决实际问题的机器学习方法.实际应用中很多场景下的学习都属于小样本学习, 如儿童通过画本上的几张图像即可“认识”老虎或者大象[12].这种通过少量的增量学习获得新的分类能力的方法, 称作微调或知识蒸馏.小样本学习的一个解决方案是结合元学习(meta learning)方法, 该方法在学习类间区别时还要保证模型的泛化能力, 使能在现有模型的基础上对新类别进行分类.小样本学习的训练是在几个种类下针对少量样本[13]进行的.当模型训练时, 先从中选取C个类别, 每类选取K个样本(样本数量为C×K个), 这些数据构成元学习模型的支持集；再从剩余类别抽取一些作为预测对象, 即C-wayK-shot问题, 从C×K个样本中学会区别C个类别, 显然增大C会增加难度, 增大K会降低难度.

1.2 对比学习

对比学习是一种空间映射方法, 其目标在于通过学习编码器对数据进行编码, 使编码后的数据便于在隐空间聚类[14].这里将对比学习的思想抽象, 如用空间视角考虑对比学习, 如图1所示.由图1可见, 正样本间的距离小, 负样本间的距离大, 对任意数据x, 如以其为锚点, 则最终学习目的就是通过编码器f使正样本与锚点的距离远小于负样本与锚点的距离.

1.3 孪生网络

孪生网络通常用于执行训练样本不充分的分类任务, 是一种在学习过程中对两个需对比的输入数据使用相同权重的同结构网络进行处理的网络结构.基于样本相似度方法, 孪生网络从输入样本中学习不同样本的相似性度量[15], 在测试时, 根据相似性程度判定样本属于哪一类别.对比学习端到端方法如图2所示.图2中两个子网络的结构和参数完全相同, 在某些系统中甚至是由一个网络并行调用了两次实现的, 通过对成对的输入样本(x1,x2,y), 利用对比度损失函数进行训练, 使同类别的一对样本间距离随训练轮次不断变小, 同时使不同类间样本距离变大.

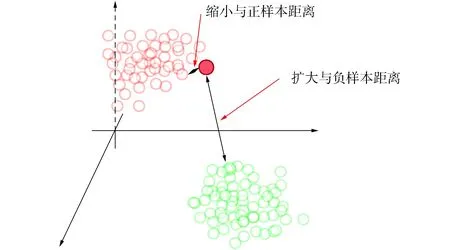
图1 对比学习方法示意图Fig.1 Schematic diagram of contrastive learning method

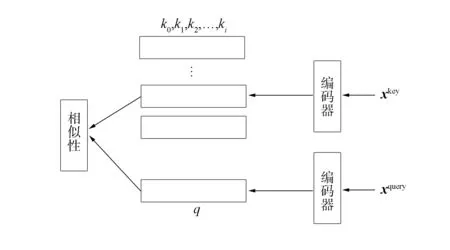
图2 对比学习端到端方法Fig.2 Contrastive learning by end-to-end ways

2 模型设计

2.1 多尺度特征提取

在深度神经网络的特征提取过程中, 通常越深层的网络提取到的特征图越抽象, 特征之间的关系也越复杂.在进行图像分类时, 神经网络会在一个小区域内频繁地进行特征对比, 这种性质使在对应区域内进行最大值池化有助于突出特征.为防止小样本学习中常见的过拟合问题, 在特征嵌入部分设计了多尺度的重叠滑动池化方式突出特征图中的判别特征, 以这种简单方法对不同层次的特征进行互补.在小样本图像学习中, 常用的特征嵌入模块是以卷积神经网络为基础构成的, CNFS的设计中也采用了类似的结构, 并且在此基础上设计了复合的多尺度重叠滑动池化层, 如图3所示.

图3 特征嵌入模块Fig.3 Feature embedded module

为更好地突出特征图中的分类特征, 设计不同尺寸的池化核组合成一组多尺度重叠滑动池化层.为网络设计方便, 在保证网络性能的前提下设计了不改变特征图尺寸的滑动池化层, 在该组合滑动池化层中分别使用尺寸为6×6,6×2,2×6的3种卷积核.组合滑动池化层在实现过程中由3层等尺寸的滑动池化层组合而成： 第一层池化核为6×6, 特征图填充为池化核同方向尺寸的一半[3,3], 步长为[1,1]；第二层池化核大小为6×2, 填充仍然为池化核同方向尺寸的一半[3,1], 步长为[1,1]；最后一层池化核大小为2×6, 填充仍然为同方向的池化核尺寸的一半[1,3], 步长也为[1,1].这3种尺度依次对应得到3种特征图, 又因为每层步长和填充设置一致, 所以它们分别输出的特征图在合并时不需要额外处理.利用这种多尺度池化方法不仅可获得更精准的特征, 还能提升整体网络模型对图像分类的准确率和检测精度.

2.2 分类度量模块

在度量模块中, 利用余弦相似度度量输入特征数据的相似度.当训练集有N个样本时, 对于任意一个样本xi∈d, 给定一对样本xi和xj(j=i+kmodN), 将经过嵌入模块后的特征向量记作X,Y, 其在特征空间的余弦相似度计算公式为

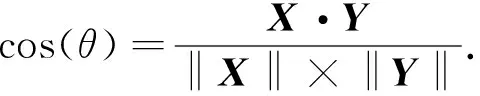
(1)

如果是二维空间, 可得如下形式：

(2)

对于多维特征向量, 利用嵌入空间中两个特征的夹角余弦值衡量两个特征之间差异的大小, 相似度值越大表示两个样本越相似, 用公式表示为

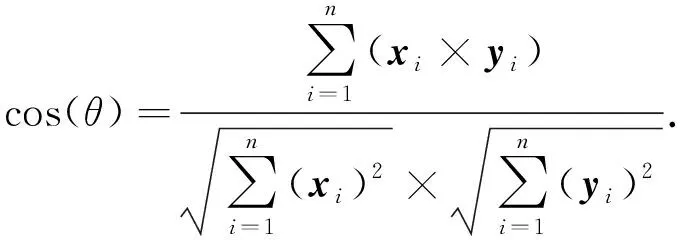
(3)

2.3 损失函数

在孪生神经网络进行对比学习的过程中, 用于指导模型参数训练的损失函数衡量的不是图像间分类的距离, 而是特定图像间的距离.因此, 采用如下的对比损失:

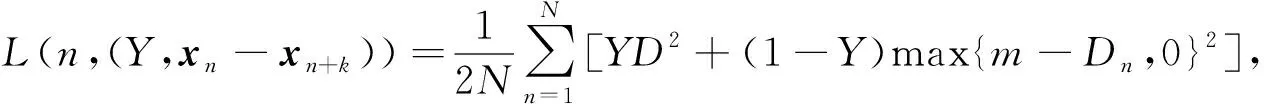
(4)

其中

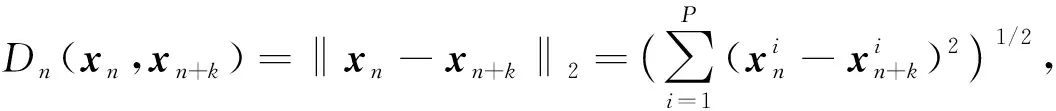
(5)

式中Dn表示抽样样本对xn和xn+k的二范数距离,Y表示两个样本是否匹配的标签,Y=1表示输入样本相似,Y=0则表示不相似,m是设定的阈值,N是样本个数.所以对于孪生神经网络, 当输入同一张图像时, 二者之间的距离小, 损失也小；当输入不是同一张图像时, 距离大, 损失也大.即要最小化相同类数据之间的距离, 最大化不同类之间的距离.而上述损失函数既可很好地表示输入样本间的相似匹配度, 也能更好地训练特征模型.

当Y=1即样本匹配, 损失函数的值需随特征间的距离单调递增, 损失函数为

(6)

当Y=0即样本不匹配时, 损失函数的值需随特征间的距离单调递减, 损失函数为

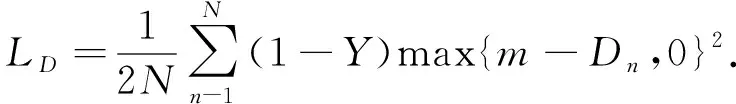
(7)

2.4 整体模型构建

基于对比学习和孪生网络的小样本识别算法的核心思想是在嵌入空间中学习图像特征之间的距离或相似度函数, 通过寻找邻近类别, 根据得到的待分类样本与已知分类样本之间的距离, 最终确定待分类样本的分类结果.分类算法主要分为两个阶段： 1) 分别提取支持集和查询集的图像特征, 并将图像映射到特征嵌入空间；2) 比较支持集特征与查询集特征之间的距离, 最后采用度量算法对测试图像进行分类.

图4 CNFS整体模型框架Fig.4 Framework of CNFS model

目前, 大多数基于对比学习的小样本模型仍存在识别率低的问题, 这主要是因为模型仅使用具有语义信息的顶层特征, 而忽略了对小样本识别也至关重要的低层特征, 使得提取到的图像特征不具有充分的表达能力, 对易混淆物体的识别也较困难.因此, 本文提出的系统基于对比学习的小样本网络CNFS模型, 并结合多尺度重叠滑动池化, 整体模型框架如图4所示.由图4可见, 本文模型框架由支持集(B)、查询集(G)、特征嵌入模块(J)和度量模块(K)组成, 通过特征嵌入模块提取到支持集和查询集的特征并映射到特征空间中, 然后在度量模块中计算样本特征向量的余弦相似度, 相似度越高样本越相似, 样本间距离越近, 相反, 若相似度值低则表示样本不相似, 距离也相对较远.

2.5 模型训练

CNFS模型采用传统的随机批梯度下降方法时收敛速度较慢, 为更好地进行C-wayK-shot的小样本学习, 本文设计了分层次更新参数的网络训练算法.在K-shot(K个学习样本)的学习任务下, 从B(G)分布中随机采样一个新任务Gi, 在任务Gi的样本分布Xi中随机采样K个样本, 用这K个样本训练模型, 获得损失, 实现对模型f的内循环更新.然后再采样Query(查询)个样本, 评估新模型的损失, 对模型f进行外循环更新.重复上述过程, 最终使模型按任务分布B(G), 在训练时较快收敛, 并能得到泛化性良好的训练结果.

算法1模型训练算法.

B(G): 任务的分布;

α,β: 两个学习率;

初始化参数集合0;

while

从目标分布中抽取一批数据Gi←B(G);

forGi：

从集合Gi中随机采样K个数据D={Xj,Yj}；

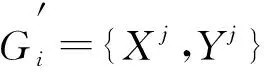
end for

end while.

模型采用的损失函数为对比损失, 以式(4)的形式计算.在损失函数中引入阈值margin, 为控制不相似样本间距离过大, 将范围控制在0～margin内, 如果超过阈值, 则损失可视为0.图5为损失函数值与样本间特征距离的关系, 其中虚线表示相似样本的损失值, 实线表示不相似样本的损失值.

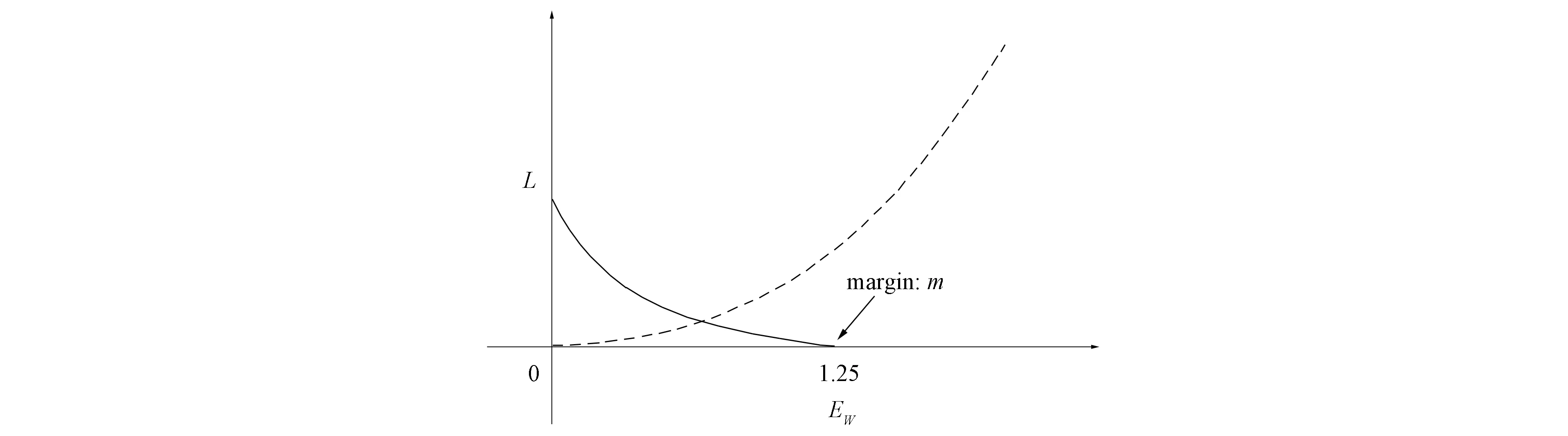
图5 阈值损失函数Fig.5 Threshold loss function

3 实 验

3.1 实验环境

实验操作系统为Ubuntu20, 程序设计语言为Python3.7, 采用机器学习框架Paddle Paddle的2.02版本, 硬件环境为CPU 4核, 内存32 GB, 显存32 GB, 磁盘512 GB, GPU Tesla V100.

3.2 实验数据与预处理

将模型在两个小样本学习常用的标准数据集Omniglot和MiniImageNet上进行系统验证.数据集Omniglot是人类手写符号集合, 包含50个不同的字母表共1 623类手写字符, 每类含有20个不同人手绘的20个灰度图像数据样本, 该数据集类别较多但每类样本数据量很少, 适用于小样本学习.数据集MiniImageNet是Google公司的Deep Mind在大数据集ImageNet上构造的小样本标准数据集, 包含100个类别, 每类600张84×84的彩色图像, 共60 000张.实验分别采用数据集Omniglot和MiniImageNet的训练集, 在训练集上进行多种数据增强, 如特定角度旋转、加入噪声(模糊增强)、剪切拼贴(软标签增强)等方法将数据集扩展到10倍数据量.实验数据集基本信息列于表1.

表1 实验数据集基本信息

实验基于5-way 1-shot, 表示在测试阶段执行5个分类任务, 每个类别提供1个支持样本, 将批处理大小设为600, 进行2 000轮训练, 每轮训练随机从训练集中取出50个类别的字符图像, 每类字符取1张图像作为支持样本, 取5张图像作为查询样本.验证模型时, 随机从训练集中取出5个类别的字符图像, 每类字符取1张图像作为支持样本, 取15张图像作为查询样本.为保证验证结果的可靠性, 多取一些样本作为查询集, 在实验中选取充分利用显存的批量数据以提高训练效率.

3.3 实验结果及分析

在两个标准数据集Omniglot和MiniImageNet上进行分类任务的交叉验证, 复现了经典的小样本方法MAML和TADAM, 并在相同的参数设置和软硬件配置条件下与CNFS模型性能进行比较.为凸显小样本学习的特殊性, 还将经典的网络VGG和Resnet引入到实验中.分别使用VGG,Resnet和改进的CNFS模型在小样本数据集上进行分类问题比较实验, 并进行多个模型之间形成滑动池化、小样本优化和按层次更新参数这3种方法的消融对比.各模型在进行2 000轮训练保证收敛后, 在分类任务的测试集上10轮测试平均准确率结果列于表2.

表2 各模型消融实验结果对比

由表2可见, 通用的分类方法VGG和Resnet在小样本数据集上的性能较差, 在同样超参数设置下它们在测试集上的预测效果都不如其在普通图像分类数据集上的性能.CNFS模型在数据集Omniglot和MiniImageNet上的性能不仅超过了通用的分类方法, 也超过了经典小样本方法MAML和TADAM.模型使用多尺度池化获得的特征信息不仅能解决低数据问题, 而且还能使模型在不同尺度下获得有利于图像分类的有效特征信息；通过对孪生神经网络输入的成对样本进行相似度匹配, 得到待测样本的类别和准确率.

综上所述, 小样本学习方法的主要目标是训练一个泛化能力较强的特征处理器.改进模型以对比学习为主要结构, 结合孪生网络方法并在网络中的特征嵌入部分加入多尺度滑动池化方法, 模型训练部分采用类似嵌套的小样本元学习训练算法.在两个经典的小样本数据集上进行实验, 分别与常用的机器视觉模型和小样本模型做交叉验证实验, 实验结果证明了本文模型在同等条件下有更好的效果和泛化能力.