3D打印火箭壳体Kagome蜂窝加筋结构压溃性能预测和实验验证
祝雪峰, 杨子康, 徐隆坤, 徐金亭, 胡 平
(大连理工大学 汽车工程学院, 辽宁 大连 116024)
0 引 言
蜂窝结构是典型的多孔结构, 具有平面内二维单元阵列、平面外平行堆叠和周期性拓扑分布的特征.蜂窝结构相比其基体材料具有更高的孔隙率和更低的质量密度, 因此具有较高的比刚度[1]、比强度[2]和比吸能[3-4], 广泛应用于航空航天[5]、汽车工程[6]以及医疗设备[7]等领域.在各种蜂窝结构中, Kagome蜂窝结构具有较好的机械性能和力学性能[8-10].Kagome蜂窝结构由六边形蜂窝结构和三角形蜂窝结构组合形成, 如图1所示.Kagome蜂窝在能量吸收、超分子结构、量子材料和可编程材料等领域应用广泛.Zhang等[11]推导出了各向同性N-Kagome单元的等效力学性能;Hyun等[12]采用拓扑优化和H-S弹性模量上界法, 证明了Kagome蜂窝结构切边模量优于等边三角形蜂窝;为提高Kagome蜂窝的平面刚度, Sun等[13]提出了分级结构的各向异性蜂窝(AMHH);Wang等[14]提出通过优化Kagome蜂窝结构的相对密度和单胞结构大小, 获得了更优的散热性能以及更好的多功能性;Hutchinson等[15]研究了Kagome桁架的刚度、强度以及致动特性;徐胜利等[16]推导出了正交各向异性Kagome蜂窝材料的宏观等效力学性能;Niu等[17]推导出了周期性正交各向异性Kagome蜂窝结构的面内力学性能的解析公式以及波在其结构中传播的性质.
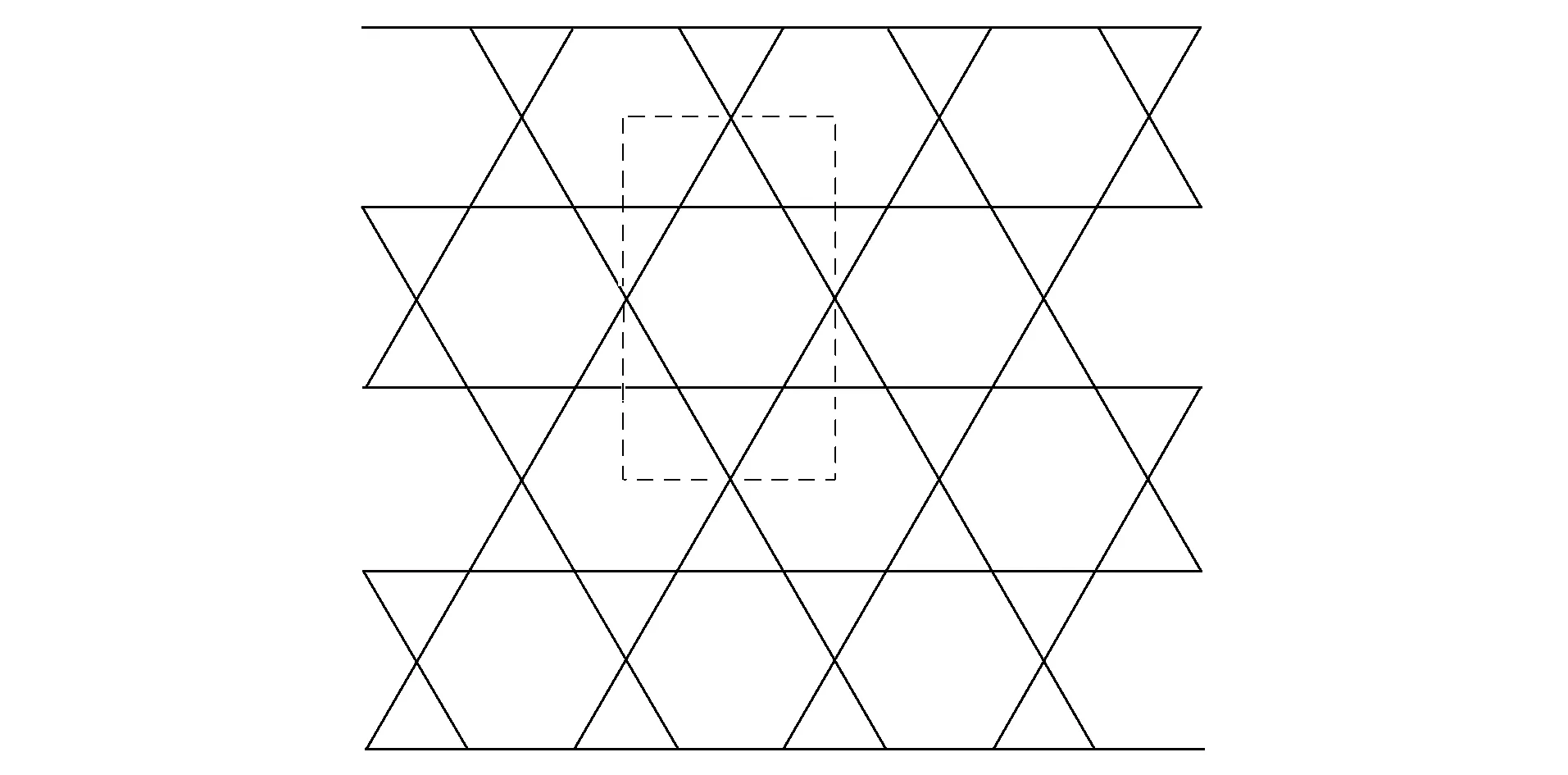
图1 Kagome蜂窝二维平面结构Fig.1 Two-dimensional plane structure of Kagome honeycomb
目前, Kagome蜂窝结构的制造方法主要有两种: 通过传统机械加工方法制造金属Kagome蜂窝结构以及使用3D打印技术[18]制造蜂窝结构.金属材质的蜂窝结构与3D打印制造的蜂窝结构相比, 其结构整体刚度和强度更高.由于材质不同, 二者的单胞在承力方面差异明显, 因此描述二者压溃过程存在差别.金属材质蜂窝的压溃过程[19-20]一般包括弹性变形阶段、屈曲变形阶段和密实阶段;3D打印制造蜂窝结构的压溃过程[21]一般包括弹性变形阶段和屈曲变形阶段.当金属材料发生屈曲变形时, 虽然被破坏的单胞发生塑性变形, 但仍具有承受载荷的能力, 而3D打印制造的蜂窝结构在屈曲阶段便失去了承受较大载荷的能力, 因此对3D打印制造的蜂窝结构在单胞发生屈曲变形时便可认为其结构失效.火箭箭体外壳通常是薄壁结构, 传统机械加工易使其屈曲变形, 且材料利用率低、3D打印技术可精确控制复杂结构的加工过程, 减少材料浪费, 并可有效避免蜂窝结构在加工过程中的屈曲变形.
火箭箭体内部蜂窝结构通常包括正置正交、等三角和斜置正交加筋.实验表明, 通过铣削技术得到的金属火箭箭体斜置正交加筋结构不易屈曲, 具有较好的抗压溃性能.在各种箭体加筋蜂窝结构中, 为研究斜置正交的3D打印火箭箭体加筋结构是否具有最优的力学性能, 本文通过推导Kagome蜂窝的力学参数表达式, 预测Kagome蜂窝加筋结构在各向同性时抗压溃性能最好, 并通过实验观察不同结构角度的Kagome蜂窝加筋结构在单轴测试时的压溃表现, 得到具有最大弹性模量以及最大剪切模量的最优结构角度, 对火箭箭体外壳设计有一定的参考价值.
1 力学分析
在研究蜂窝结构的压溃性能时, 单胞的结构强度决定整体结构强度, Kagome蜂窝加筋柱壳结构尺寸远大于Kagome蜂窝的单胞尺寸, 因此可简化为二维平面上单个单胞的力学性能分析.设Kagome蜂窝结单胞细胞壁的竖直方向为打印方向,细胞壁的厚度为t, 蜂窝结构的离侧面宽度为ω.
蜂窝结构中的各向异性率和相对密度可用于衡量结构性能.各向异性率是材料测试中的重要参数.各向异性率旨在表现材料在不同方向的物理和化学特性, 是衡量在不同方向力学性能的关键参数.Kagome蜂窝结构的各向异性率定义为
(1)
其中a1,a2,b1,b2表示Kagome蜂窝单胞的结构参数, 如图2所示.
相对密度是多孔材料的重要结构参数.蜂窝材料作为典型的多孔材料, 相对密度旨在表现蜂窝结构的结构特征, 是决定蜂窝结构力学性能的关键因素.Kagome蜂窝结构的相对密度定义为
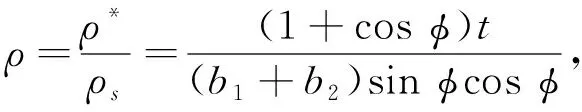
(2)
其中ρ*表示蜂窝的密度,ρs表示制造该蜂窝固体材质的密度.
根据以上网络预测值与实际值的对比,可以看出,所构建的GRNN网络的预测值和实际值比较接近,网络具有较好的预测能力,误差较小,可以用于瓦斯涌出量的预测。
正交各向异性Kagome蜂窝是Kagome蜂窝的一种特殊结构, 由一组弹性对称面组成.正交各项异性Kagome蜂窝的二维柔度矩阵C的表达式为

(3)
其中E1和E2分别表示x和y方向上的弹性模量,υ12和υ21分别表示x和y方向上的Poisson比,G12表示剪切模量.
选取单胞为研究对象, 分别施加不同方向的应力条件, 图3为Kagome蜂窝单胞结构压拉受力示意图.先计算单胞在不同方向的变形, 同时考虑单胞的变形协调条件, 再联立方程求解得到柔度矩阵表达式.柔度矩阵C的解析表达式为
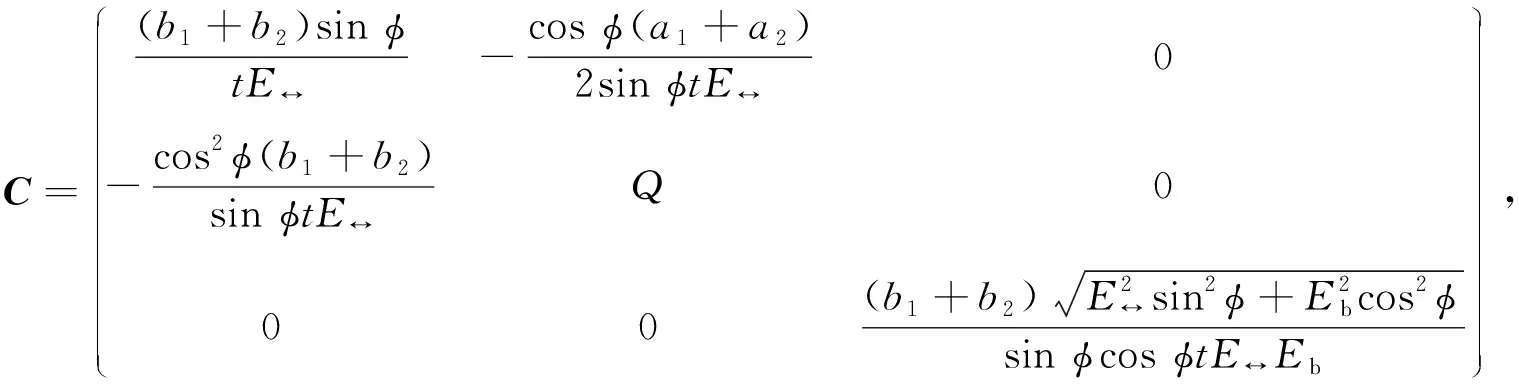
(4)

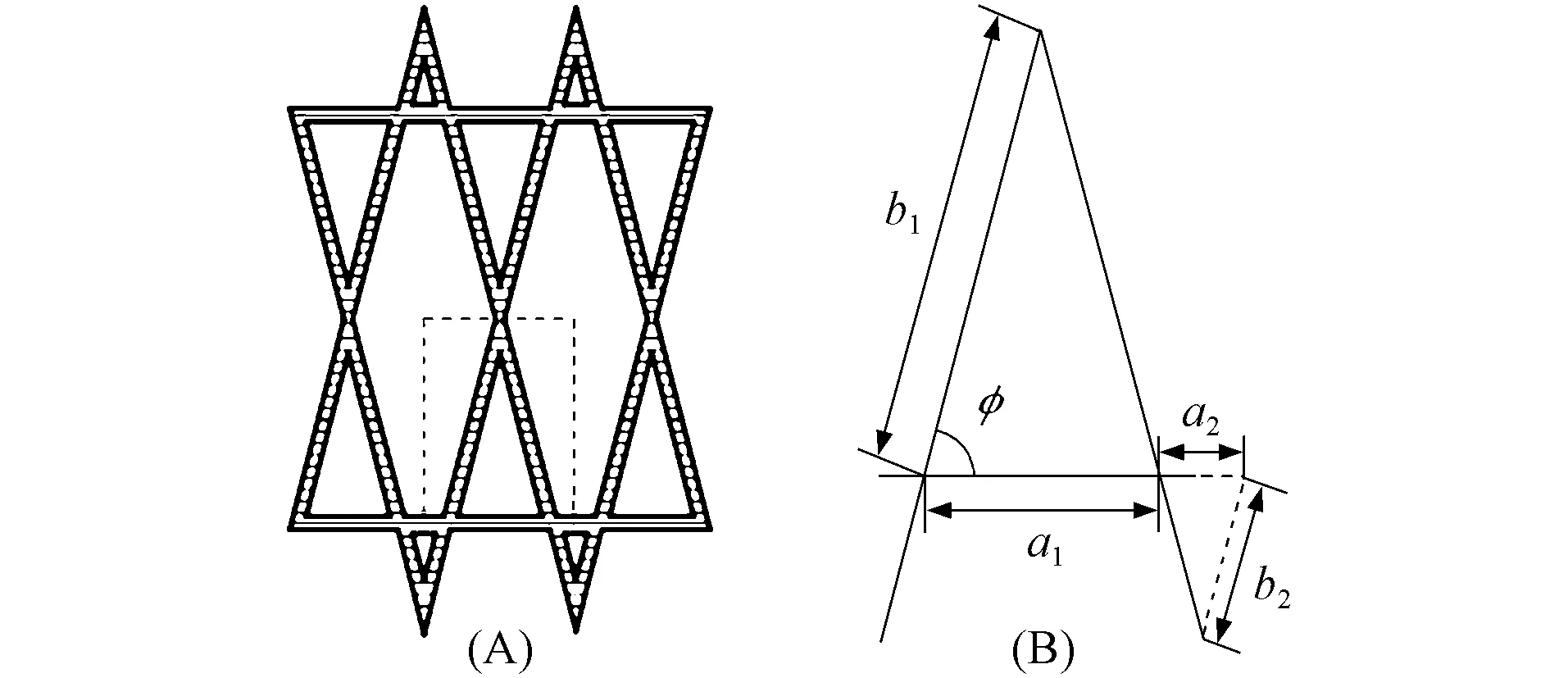
图2 Kagome蜂窝平面结构(A)及其参数的示意图(B)Fig.2 Kagome honeycomb plane structure (A) and schematic diagram of its parameters (B)
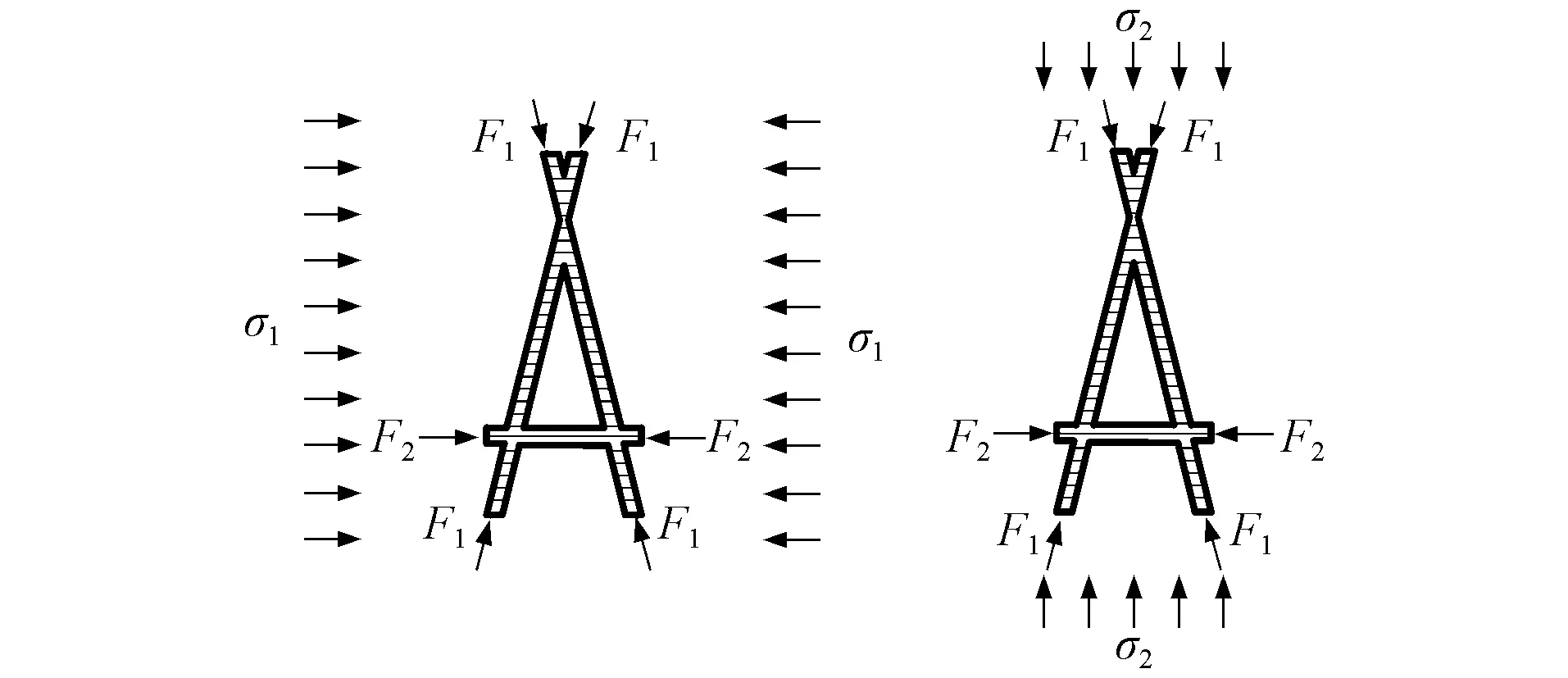
图3 Kagome蜂窝单胞结构压拉受力示意图Fig.3 Schematic diagram of compression and tension force of Kagome honeycomb cell structure
对柔度矩阵中剪切模量G12的表达式进行简化,使用相对密度和各向异性率表示剪切模量, 化简后可得
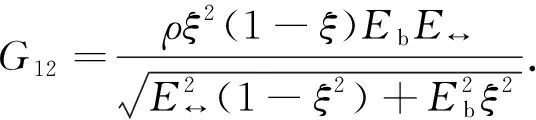
(5)
同理使用相对密度和各向异性率对E1和E2表达式进行化简, 化简后可得

(6)

(7)

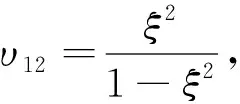
(8)
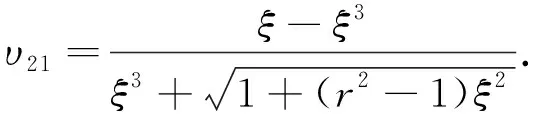
(9)
由式(6)~(9)可知, Kagome蜂窝结构在一般情况下υ12≠υ21且E1≠E2, 联立式(8)和式(9)可得
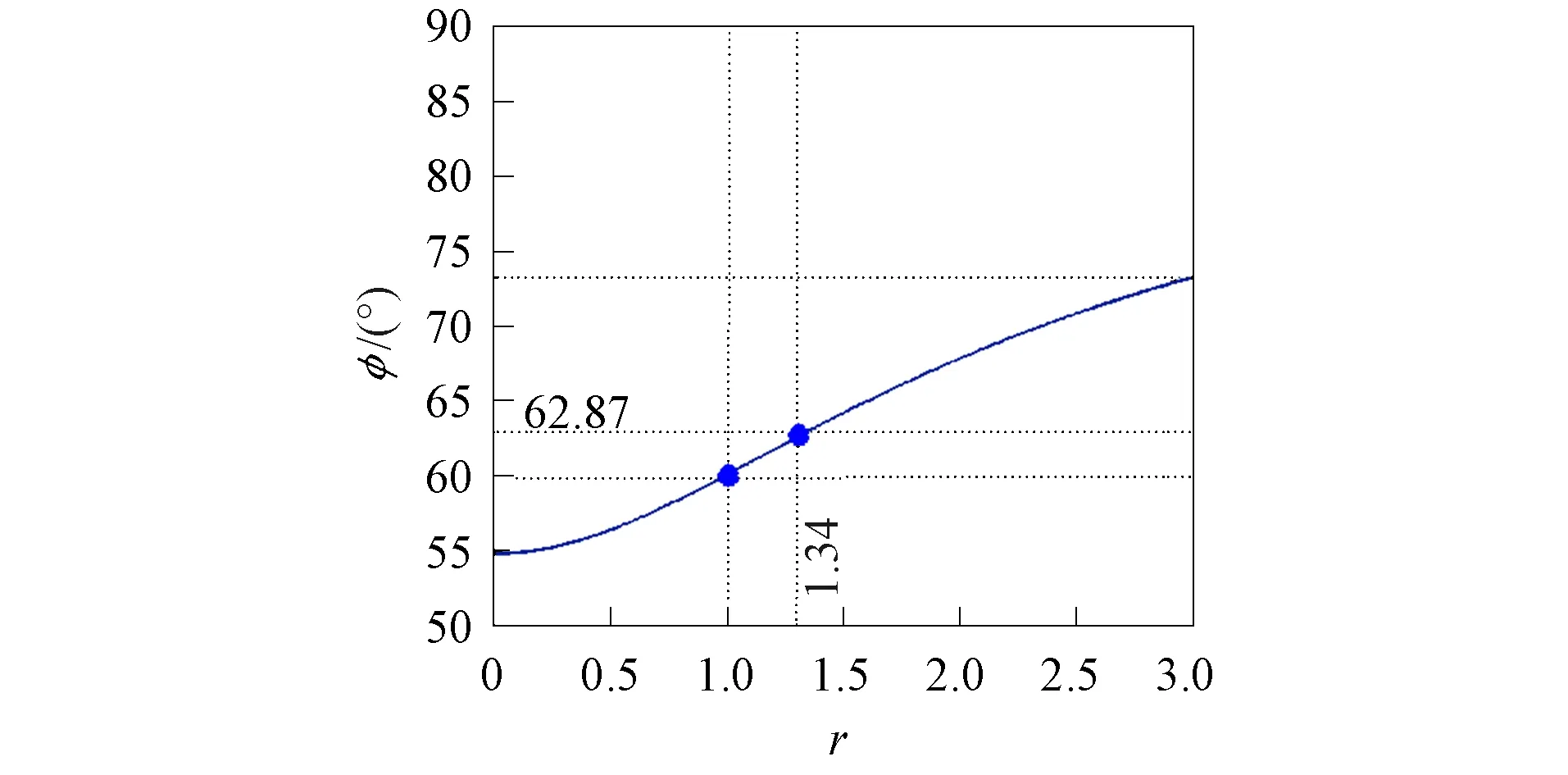
图4 φ和r的关系Fig.4 Relationship between φ and r
使得υ12=υ21且E1=E2.φ和r的关系如图4所示.
由图4可见, 当Kagome蜂窝结构的角度φ=62.87°时, 3D打印的Kagome蜂窝结构呈各向同性, 此时结构在各方向的力学性能相同.当使用不同材料时, 其y轴方向的等效弹性模量Eb和x轴方向的等效弹性模量E↔不同, 因此得到蜂窝结构各向同性的结构角度也不同.
2 实 验
2.1 实验样件设计
选取各向同性的Kagome蜂窝结构与常用各向异性的Kagome蜂窝结构进行抗压溃实验对比.实验分别选取φ=62.87°和φ=75°两种不同结构的Kagome蜂窝结构, 设计并制造这两种角度的Kagome蜂窝加筋结构, 实验样件模型如图5所示.
工程实践中为增强结构的抗压溃性能多使用加筋柱壳结构, 以增强结构整体的抗压溃性能.因此, 除设计上述两种不同结构角度的Kagome蜂窝加筋结构外, 还需设计Kagome蜂窝加筋柱壳结构.加筋柱壳结构的设计同样需考虑不同结构角度的Kagome蜂窝.Kagome蜂窝加筋柱壳结构设计模型如图6所示, 模型结构的参数列于表1, 其中a1,a2,b1,b2,φ表示Kagome蜂窝结构的基本参数,ρ表示相对密度,tr和t分别表示三维Kagome蜂窝加筋柱壳结构的筋条厚度和蒙皮厚度, 如图7所示.

图5 φ=62.87°(A)和φ=75°(B)的 Kagome蜂窝加筋结构Fig.5 Kagome honeycomb stiffened structure with φ=62.87° (A) and φ=75° (B)

图6 φ=62.87°(A)和φ=75°(B)的 Kagome蜂窝加筋柱壳结构Fig.6 Kagome honeycomb stiffened cylindrical shell structure with φ=62.87° (A) and φ=75° (B)

表1 Kagome蜂窝加筋柱壳结构的参数
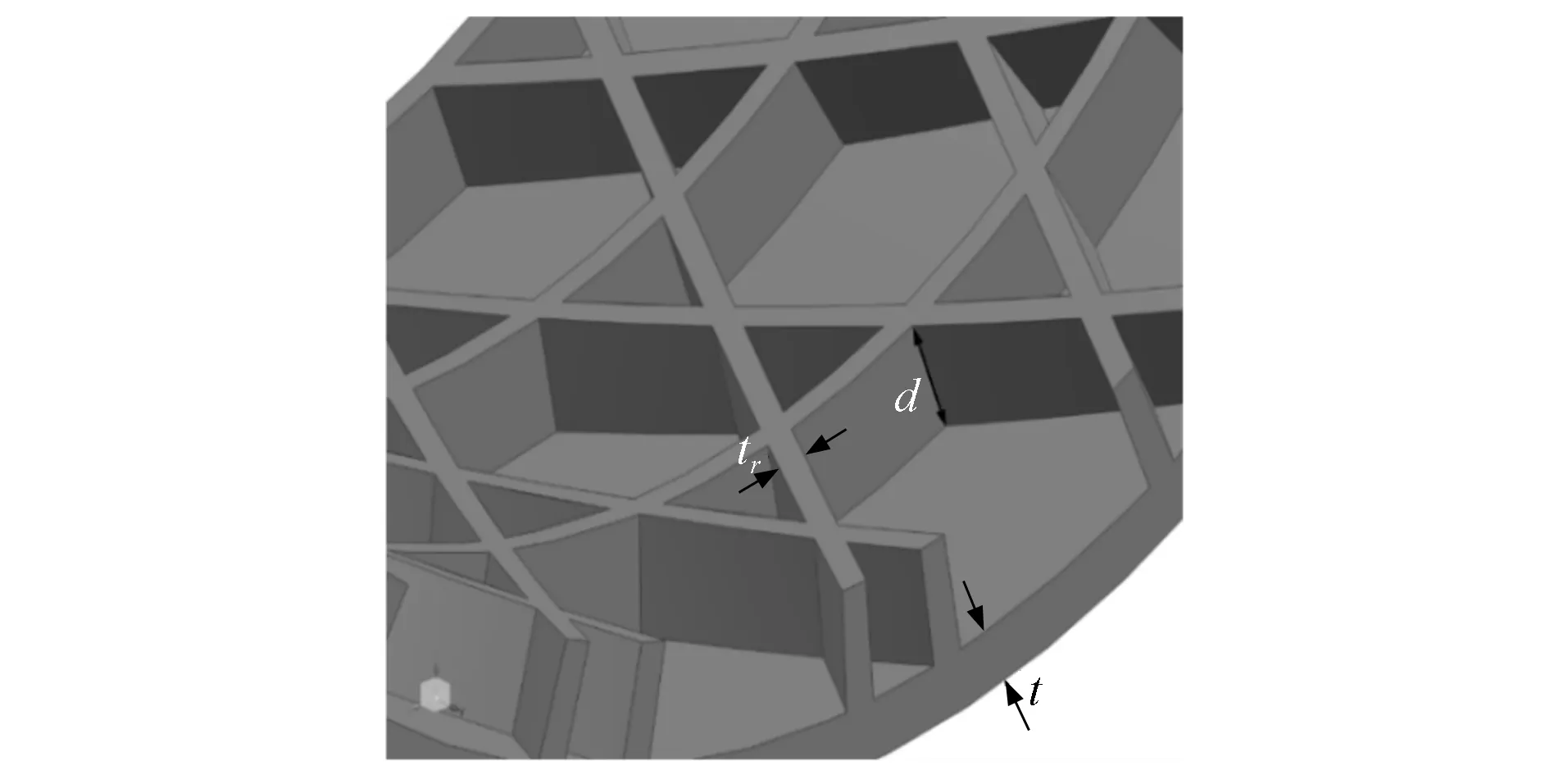
图7 Kagome蜂窝加筋柱壳三维结构尺寸示意图Fig.7 Schematic diagram of three-dimensional Kagome honeycomb stiffened cylindrical shell structure size
为保证实验的准确性, 需增加斜置正交蜂窝结构, 斜置正交蜂窝结构是工程中常见的一种蜂窝结构, 广泛应用于质量小, 但需承载较大轴向力的场合.斜置正交蜂窝结构三维模型及其二维平面尺寸如图8所示.
为保证对照实验的可靠性,tr1,d1,t1取与表1中对应参数相同的值, 平行筋条间距c=7.74 mm, 筋条与水平呈45°.
2.2 实验样件制作
实验样件选用波兰Zortrax公司生产的Zortrax-M200型3D打印机对样件进行打印, 打印材料选择丙烯腈-丁二烯-苯乙烯(ABS)塑料, 打印层厚度为0.19 mm.实验所需制作的样件如图9所示.
2.3 单轴压缩实验及结果
单轴拉伸实验设备选用长春科新试验仪器有限公司生产的WDW-100型微机控制式电子万能试验机, 实验中将试件置于试验机的两个压盘之间, 两个压盘厚度均为0.02 m, 其直径均为0.098 7 m.为方便观测压溃现象, 获取更精确的实验数值并确保实验的准确性, 在实验中需使压溃速度尽量小, 以保证整个压缩过程呈准静态, 下压速度选择0.016 7 mm/s.

图8 斜置正交加筋柱壳三维CAD模型(A)及其结构的二维尺寸(B)Fig.8 3D CAD model of oblique orthogonal stiffened cylindrical shell (A) and 2D dimensions of its structures (B)

图9 φ=62.87°(A)和φ=75°(B)的Kagome蜂窝加筋结构,φ=62.87°(C)和φ=75°(D)的Kagome蜂窝加筋柱壳结构及斜置正交加筋柱壳结构(E)Fig.9 Kagome honeycomb stiffened structure with φ=62.87° (A) and φ=75° (B),Kagome honeycomb stiffened cylindrical shell structure with φ=62.87° (C) and φ=75° (D) and oblique orthogonal stiffened cylindriacl shell structure (E)

图10 试件a实验前(A)和实验后(B)的示意图Fig.10 Schematic diagram of specimen a before (A) and after (B) experiment
试件a的抗压溃实验过程如图10所示.由图10(A)可见: 实验中试验机产生的实验力持续且缓慢上升, 当实验力为3 106.79 N时, 试件a发生明显变形;当试验机上侧圆盘的垂直位移为1.71 mm时, 实验力达到峰值3 195.24 N并迅速下降, 此时试件a被压断, 如图10(B)所示.
试件b的抗压溃实验过程如图11所示.由图11(A)可见, 实验中试验机产生的实验力持续且缓慢上升, 在试验机上侧的圆盘的垂直位移为1.13 mm时, 实验力达到峰值3 089.75 N并迅速下降, 此时试件b被压断, 如图11(B)所示.

图11 试件b实验前(A)和实验后(B)的示意图Fig.11 Schematic diagram of specimen b before (A) and after (B) experiment

图12 φ=62.87°的Kagome蜂窝薄壁 加筋柱壳结构破坏形式Fig.12 Failure form of Kagome honeycomb thin-walled stiffened cylindrical shell structure with φ=62.87°
试件c的抗压溃实验如图12所示.实验中实验力持续且缓慢上升, 当试验机上侧圆盘垂直位移为3.45 mm时, 实验力达到峰值22 985.18 N, 之后实验力缓慢下降, 当实验力为22 113.59 N时, 试件c的外蒙皮出现明显膨胀和凹陷, 此时结构发生失稳破坏.
试件d的抗压溃实验如图13所示.实验中实验力持续且缓慢上升, 当试验机上侧圆盘垂直位移为2.82 mm时, 外蒙皮出现明显内加筋的纹路, 当垂直位移为3.52 mm时, 实验力达到峰值16 180.65 N, 之后实验力缓慢下降, 当实验力为13 889.83 N时, 试件d的外蒙皮出现明显裂纹, 此时结构发生失稳破坏.
试件e的抗压溃实验如图14所示.实验中实验力持续且缓慢上升, 当试验机上侧圆盘的垂直位移为3.62 mm时, 实验力达到峰值22 653.55 N, 之后实验力缓慢下降, 当实验力为18 794.81 N时, 试件e的外蒙皮出现明显裂纹, 此时结构发生失稳破坏.

图13 斜置正交薄壁加筋柱壳结构破坏形式Fig.13 Failure form of oblique orthogonal thin-walled stiffened cylindrical shell structure

图14 φ=75°的Kagome蜂窝薄壁加筋柱壳结构破坏形式Fig.14 Failure form of Kagome honeycomb thin-walled stiffened cylindrical shell structure with φ=75°

图15 试件a和试件b的位移-力曲线Fig.15 Displacement and force curves of specimen a and specimen b
为衡量压溃性能, 实验中需记录位移和实验力两个物理量.试件a和试件b均为无柱壳加筋的Kagome蜂窝结构, 为对比各向同性的Kagome蜂窝结构与各向异性的Kagome蜂窝结构的抗压溃性能的差别, 将试件a和试件b的位移-力曲线放在同一坐标轴比对, 结果如图15所示.
在工程中常用薄壁加筋柱壳结构.因此, 为对比各向同性的Kagome蜂窝薄壁加筋柱壳结构与各向异性的Kagome蜂窝薄壁加筋柱壳结构的抗压溃性能的差别, 将试件c和试件d的位移-力曲线放在同一坐标轴比对, 结果如图16所示;为保证实验的完整性和准确性, 将各向同性的Kagome蜂窝薄壁加筋柱壳结构与斜置正交薄壁加筋柱壳结构比对, 将试件c和试件e的位移-力曲线放在同一坐标轴比对, 结果如图17所示.
第一组实验是无柱壳Kagome蜂窝加筋结构的实验对比.通过压缩实验对比φ=62.87°的试件a和φ=75°的试件b.由图15可见,φ=75°比φ=62.87°的Kagome蜂窝加筋结构的最大承载力小105.49 N, 即无柱壳各向同性的Kagome蜂窝结构优于无柱壳各向异性的Kagome蜂窝结构的抗压溃能力.
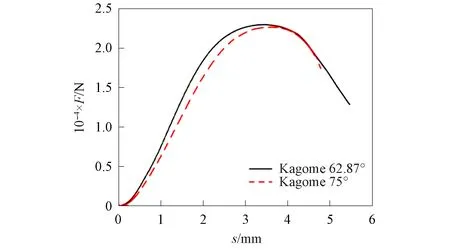
图16 试件c和试件d的位移-力曲线Fig.16 Displacement and force curves of specimen c and specimen d
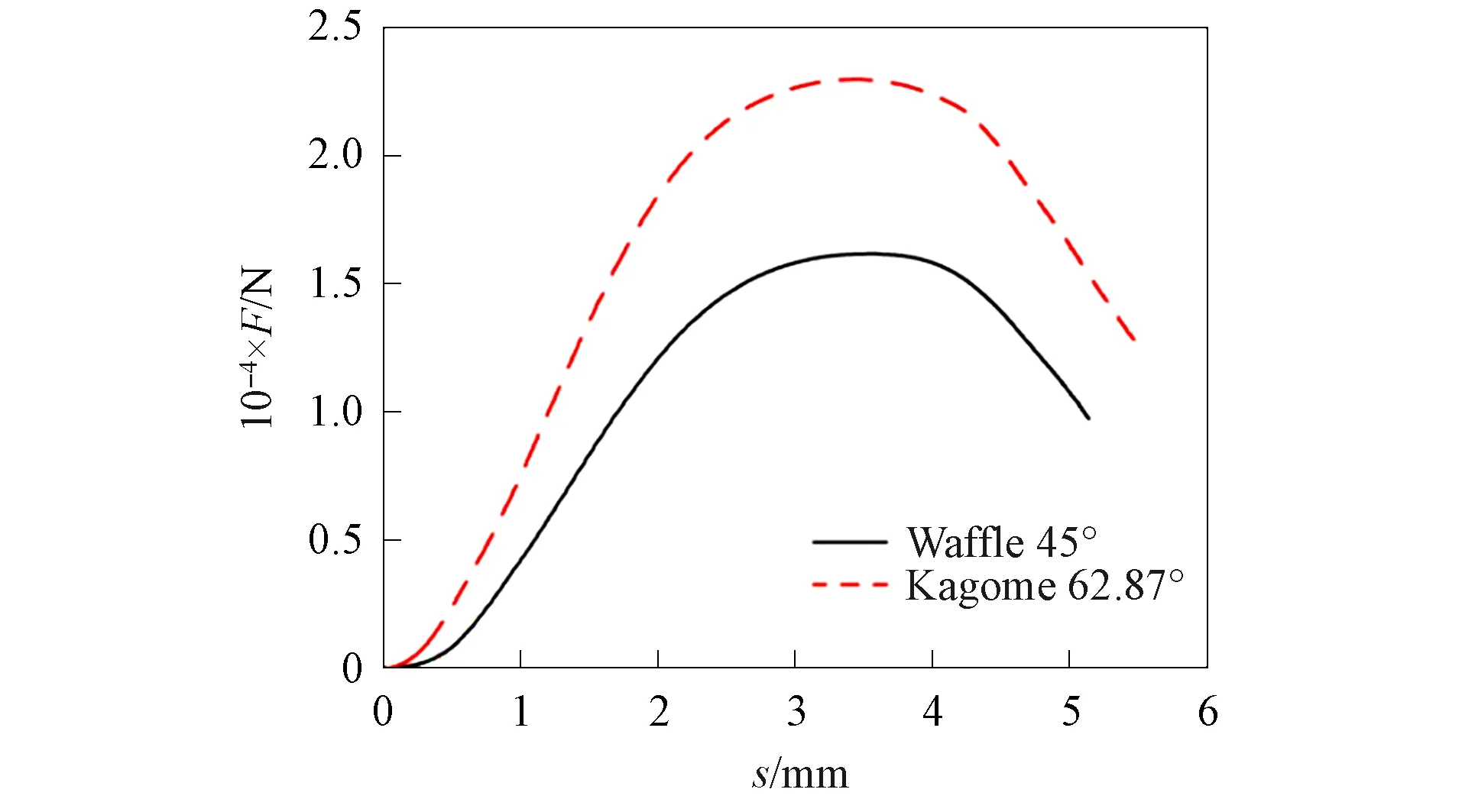
图17 试件c和试件e的位移-力曲线Fig.17 Displacement and force curves of specimen c and specimen e
第二组实验是加筋柱壳结构的实验对比, 对比实验分为两组: 一组是φ=62.87°和φ=75°的Kagome加筋柱壳结构;一组是φ=62.87°的薄壁Kagome加筋柱壳结构和斜置正交加筋柱壳结构.由图16可见,φ=75°比φ=62.87°的薄壁Kagome加筋柱壳结构的最大承载力小331.63 N.由图17可见,φ=62.87°的薄壁Kagome加筋柱壳结构的最大承载力远高于斜置正交加筋薄壁柱壳结构的承载力, 约高42.1%.因此, 各向同性的Kagome加筋柱壳结构在抗压溃性能方面表现更好.
综上, 本文研究了3D打印Kagome蜂窝加筋结构的压溃性能, 分析了蜂窝加筋结构的平面应力状态, 并推导了受力解析表达式, 得到了柔度矩阵等力学性能参数的表达式及Kagome蜂窝结构呈各向同性时的结构参数.通过3D打印机设计制造得到Kagome蜂窝加筋结构的实验样件以及Kagome加筋柱壳结构样件, 使用微机式电子万能试验机进行压溃性能对比实验.通过实验结果分析可知,φ=62.87°的Kagome蜂窝结构, 即Kagome蜂窝呈各向同性时的承载性能最佳, 表明各向同性的Kagome蜂窝结构具有更好的力学性能以及机械承载性能.
本文使用ABS塑料材质的试件, 其材料特性导致其承载能力相对较低, 无法满足在部分场景的应用, 但在推导最佳结构参数时使用的力学公式以及实验分析方法, 对不同3D打印材料制造的Kagome蜂窝结构具有一定的参考价值.近年来, 金属3D打印技术取得了重大进展, 但仍无法制造大尺寸的蜂窝结构, 其最大打印尺寸仅为400 mm×400 mm×400 mm[22], 本文为大尺寸金属3D打印Kagome蜂窝的压溃性能研究提供了参考.

