二维氯化铯与二维氯化钠之间结构关系的探讨

莫云飞, 周群益, 侯兆阳, 刘让苏，卢一兵

(1. 长沙学院电子信息与电气工程学院, 湖南 长沙 410022；2. 广东技术师范大学天河学院, 广东 广州 510540；3. 长安大学理学院应用物理系, 陕西 西安 710064；4.湖南大学物理与微电子科学学院, 湖南 长沙 410082)

1 研究背景

马德隆常数是表示离子晶体能量的一个无量纲常数.根据晶体结构，基本方法是累加法计算其近似值，但此方法收敛速度比较慢.而埃夫琴提出中性元胞法，大大提高了收敛速度[1].

氯化钠离子晶体有二维和三维之分，同理，氯化铯离子晶体也有二维和三维之分.唐为民分析的二维氯化钠晶体新结构[2]，实际上就是二维氯化铯结构，采用双埃夫琴单胞，推导了公式，设计C语言程序，计算了二维氯化钠结构的马德隆常数.许多学者都用采用各种计算机语言计算过二维氯化钠结构的马德隆常数[3-8].文章建立了二维氯化铯的嵌套结构，提出了马德隆常数的递推公式，采用迭代算法，设计MATLAB程序，高效率地计算了马德隆常数.

2 二维氯化铯晶体的单胞和嵌套结构

如图1所示，在原点取一个氯离子，顶点有4个铯离子，形成一个原胞，称为氯心单胞.顶点离子电荷有1/4在单胞里面，因此单胞的内部都是电中性的，称为埃夫琴单胞.如果将氯离子和铯离子互换，氯心单胞就变成铯心单胞，也是电中性的.设晶格常数为2a，两种单胞的面积都是S0= 4a2.

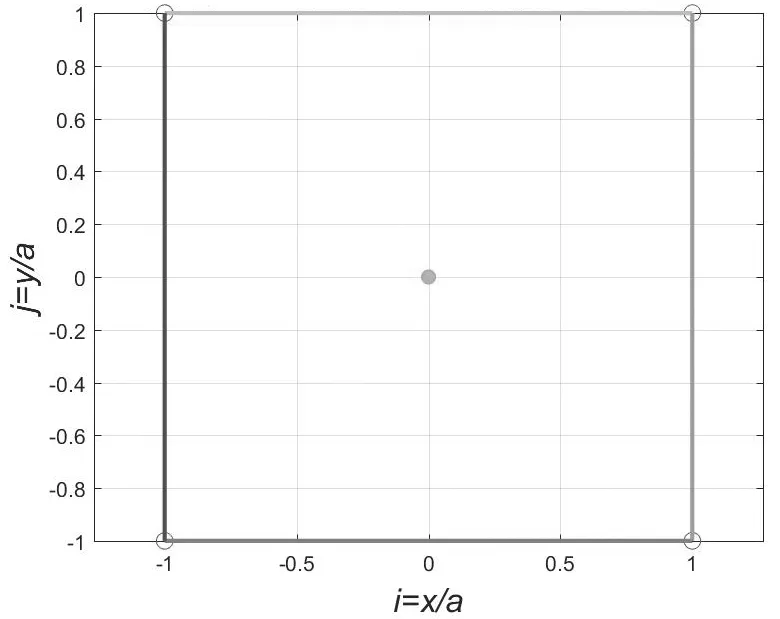
图1 二维氯化铯结构的氯心单胞(第1级氯心晶体)

使氯心单胞的一个顶点位于铯心单胞的中心，同时使铯心单胞的一个顶点位于氯心单胞的中心，氯心单胞和铯心单胞可以相互嵌入，重叠部分的面积是S0/4 =a2.这两种单胞称为互嵌单胞.

如果取氯离子为参考离子，就取氯心单胞为中心单胞，称为第1级氯心晶体.

由铯心单胞组成晶体称为铯心晶体.如图2所示，取22= 4个铯心单胞，组成第1级铯心晶体.第1级铯心晶体嵌套了第1级氯心晶体，其表面的氯离子包裹了第1级氯心晶体的全部离子.第1级铯心晶体也可以看作以第1级氯心晶体顶角的4个铯离子为中心，嵌入4个铯心单胞形成的.

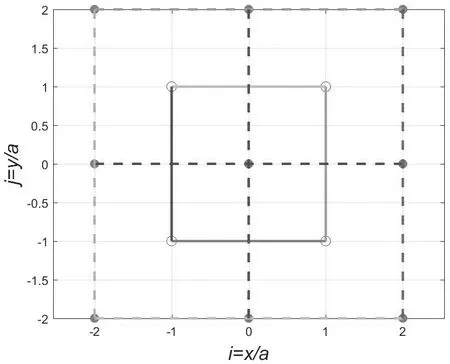
图2 二维氯化铯嵌套结构的第1级铯心晶体

图3 二维氯化铯嵌套结构的第2级氯心晶体

由氯心单胞组成晶体称为氯心晶体.如图3所示，取32= 9个氯心单胞，组成第2级氯心晶体.第2级氯心晶体嵌套了第1级铯心晶体，其表面的铯离子包裹了第1级铯心晶体的全部离子.第2级氯心晶体也可以看作以第1级铯心晶体表面的8个氯离子为中心，嵌入8个氯心单胞形成的.

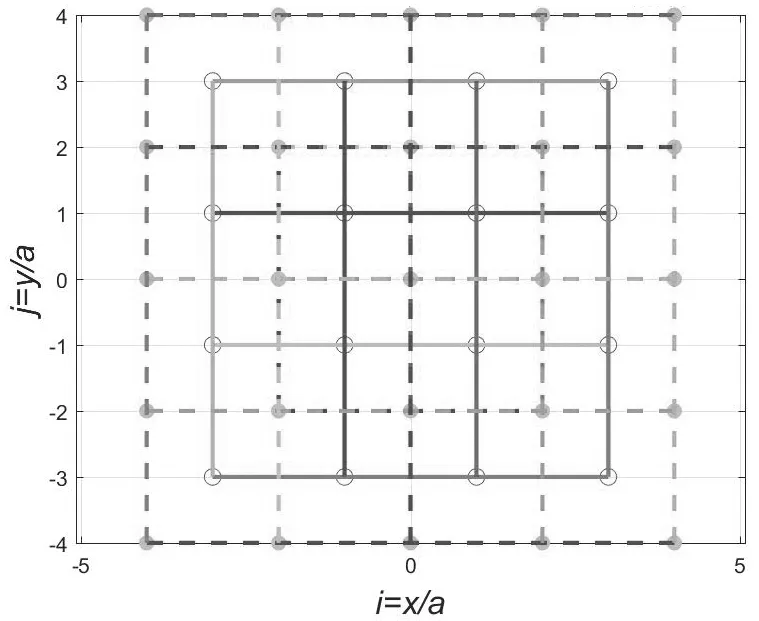
图4 二维氯化铯嵌套结构的第2级铯心晶体

如图4所示，取42= 16个铯心单胞，组成第2级铯心晶体.第2级铯心晶体嵌套了第2级氯心晶体，其表面的氯离子包裹了第2级氯心晶体的全部离子.第2级铯心晶体也可以看作以第2级氯心晶体表面12个铯离子为中心，嵌入12个铯心单胞形成的.

同理可得第3级氯心晶体和第3级铯心晶体，如图5和图6所示.

设n为正整数，第n级氯心晶体是由(2n- 1)2个氯心单胞组成的，第n级铯心晶体是由(2n)2个铯心单胞组成的.第n级铯心晶体嵌套了第n级氯心晶体，第n+ 1级氯心晶体嵌套了第n级铯心晶体.晶体的这种结构称为嵌套结构.在晶体外面嵌入单胞，形成新晶体的方法称为单胞嵌入法.

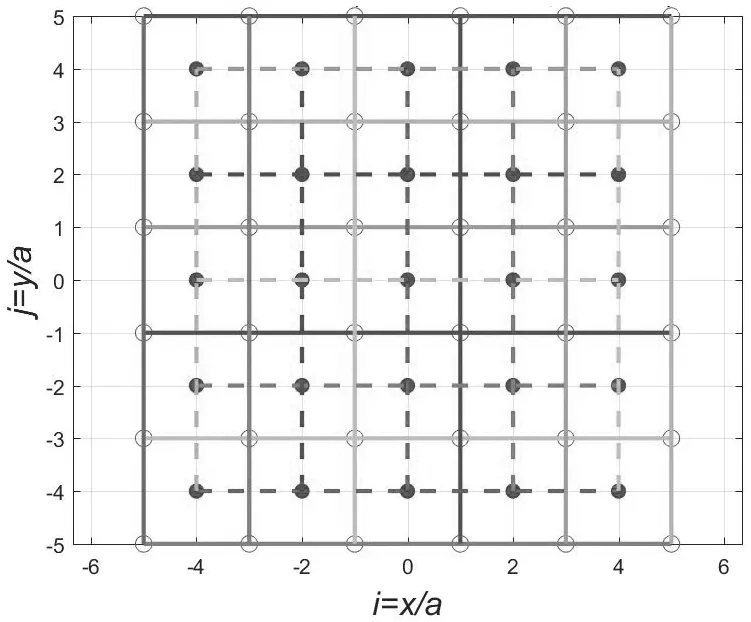
图5 二维氯化铯嵌套结构的第3级氯心晶体

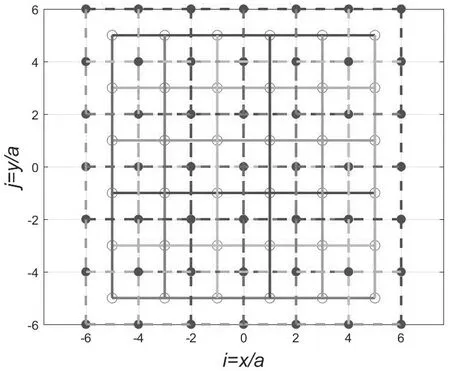
图6 二维氯化铯嵌套结构的第3级铯心晶体

注意：如果取铯离子为参考离子，就取铯心单胞为中心单胞，也能通过单胞嵌入法建立各级晶体.这并不影响最后的结果.

3 累加法的马德隆常数

对于二维氯化铯结构的晶体，正负离子之间的最近距离为

(1)

取a为坐标单位，离子的坐标就用整数表示.

对于第n级氯心晶体，晶格能为

其中，铯离子到参考离子之间的距离为

(2a)

氯离子到参考离子之间的距离为

(2b)

因此

(3)

全部离子对马德隆常数的贡献为

(n= 1,2,…)，

(4)

当n= 1时，上式第2个求和项为0.这是第一个累加法的公式.

对于第n级铯心晶体，在(2n)3个埃夫琴单胞中，全部离子对马德隆常数的贡献为

(n= 1,2,…)，

(5)

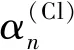
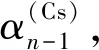
(6)

这是累加法的第一个递推公式.其中，4条边线铯离子的贡献为

(n= 1,2,…)，

(7a)

4个顶点铯离子的贡献为

(n= 1,2,…).

(7b)

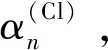
(n= 1,2,…)，

(8)

这是累加法的第二个递推公式.其中，4条边线氯离子的贡献为

(n= 1,2,…)，

(9a)

4个顶点氯离子的贡献为

(n= 1,2,…).

(9b)

一个晶体被一种单胞嵌入之后，就被新的表面离子所包裹，从而形成新的晶体；新的晶体被另一种单胞嵌入之后，又被更新的表面离子所包裹，从而形成更新的晶体；依此类推.递推公式所体现的方法称为包裹法，离子包裹的过程是通过单胞嵌入的过程形成的.只要知道边线离子的分布规律，就能用递推公式累加全部离子对马德隆常数的贡献.

图7 二维氯化铯结构的累加法的各级马德隆常数

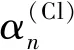
(10)

如图7所示，它们的平均值αn也是收敛的.当n= 100 000时，αn的值是1.615 542 626 695 041.王永杰等人计算[7]：当整数为10 000时，马德隆常数为

α10 000= 1.615 542 626 712 96.

邱为刚用解析解计算[9]，二维氯化钠结构马德隆常数为

α= 1.615 542 626 71.

我们的α100 000与王永杰等人的α10 000和邱为刚的α在小数点后面9位是相同的，可以猜想：二维氯化铯结构的晶体与二维氯化钠结构的晶体应该是同一晶体.

4 埃夫琴法的马德隆常数

每条边线离子有1/2在内部，每个顶点离子有1/4在内部.对于第n级氯心晶体，埃夫琴法的马德隆常数为

(11a)

这是第一个埃夫琴法的公式.由于只考虑晶体内部离子和边线离子的内部部分对马德隆常数的贡献，因此也称为内埃夫琴法公式.利用(6)式，上式可化为

(n= 1,2,…)，

(11b)

晶体边线离子的外部对马德隆常数是负面贡献，可当作一种表面效应，这是消除了表面效应的马德隆常数，是第一个外埃夫琴法的马德隆常数的公式.

对于第n级铯心晶体，埃夫琴法的马德隆常数为

(n= 1,2,…).

(12a)

这是第二个埃夫琴法的公式.利用(8)式，消除表面效应的马德隆常数为

(n= 1,2,…).

(12b)

(11)和(12)的两组公式又称为双埃夫琴法公式.

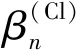
随着n的增加，埃夫琴法的马德隆常数的平均值βn逐渐增加.当n比较大时，βn的多位数字如表1所示.当n≥ 20 000时，βn与二维氯化钠结构的马德隆常数在小数点后面9位数字相同，更有理由认为：二维氯化铯结构的晶体与二维氯化钠结构的晶体应该是同一晶体.

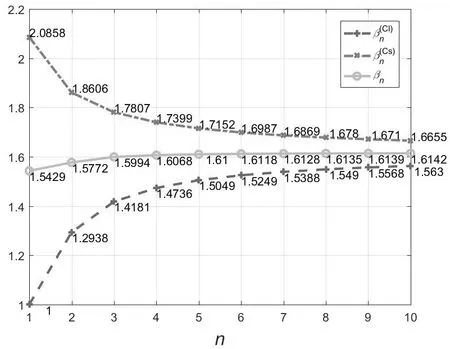
图8 二维氯化铯结构埃夫琴法的各级马德隆常数

在图2中，将四个点(2a,0)，(0,2a)，(-2a,0)和(0,-2a)连接成一个正四边形，就是一个斜的二维氯化钠结构的单胞.在图4中，将四个点(4a,0)，(0,4a)，(-4a,0)和(0,-4a)连接成一个正四边形，里面就包含了4个斜的二维氯化钠结构的单胞.同理，在图6中包含9个斜的二维氯化钠结构的单胞.

如图9所示，在二维氯化钠结构的氯心单胞中，将四个点(a,0)，(0,a)，(-a,0)和(0,-a)连接成一个正四边形，就形成一个斜的二维氯化铯结构的氯心单胞.如图10所示，二维氯化钠结构的第2级晶体由4个氯心单胞组成，里面包含了5个二维氯化铯结构的氯心单胞，也包含了4个二维氯化铯结构的铯心单胞.可见：二维氯化铯结构的晶体与二维氯化钠结构的晶体确实是同一晶体.尽管两种单胞的晶格常数不同，因而单胞的大小不同，它们的马德隆常数却是相同的.

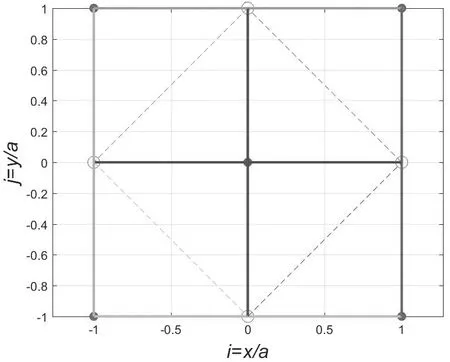
图9 二维氯化钠结构的单胞(第1级晶体)

唐为民将n取到1000，计算的常数为

α1 000= 1.615 542 126，

与邱为刚和我们的结果在小数点后面6位数字相同.可见：利用嵌套结构的马德隆公式和MATLAB计算效率更高，结果更精准.但是，与二维氯化钠基本结构的马德隆常数相比，二维氯化铯结构的马德隆常数的精度稍微差一点.这是因为：对于同一级整数n，二维氯化铯晶体中的离子数较少，所以马德隆常数的精确数字的位数较少.或者说，二维氯化铯结构的晶体需要取更大的整数，才能得到马德隆常数的更多精确数字.当然，电脑运行的时间更长.

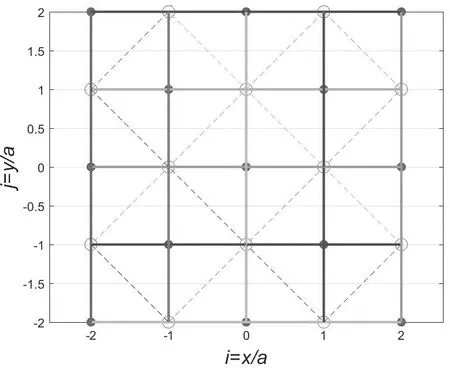
图10 二维氯化钠嵌套结构的第2级晶体

5 结论

文章通过马德隆常数和图形说明：二维氯化铯结构的晶体与二维氯化钠结构的晶体是同一晶体，具有相同的马德隆常数.也说明同一种晶体可以有不同的单胞构成方法.

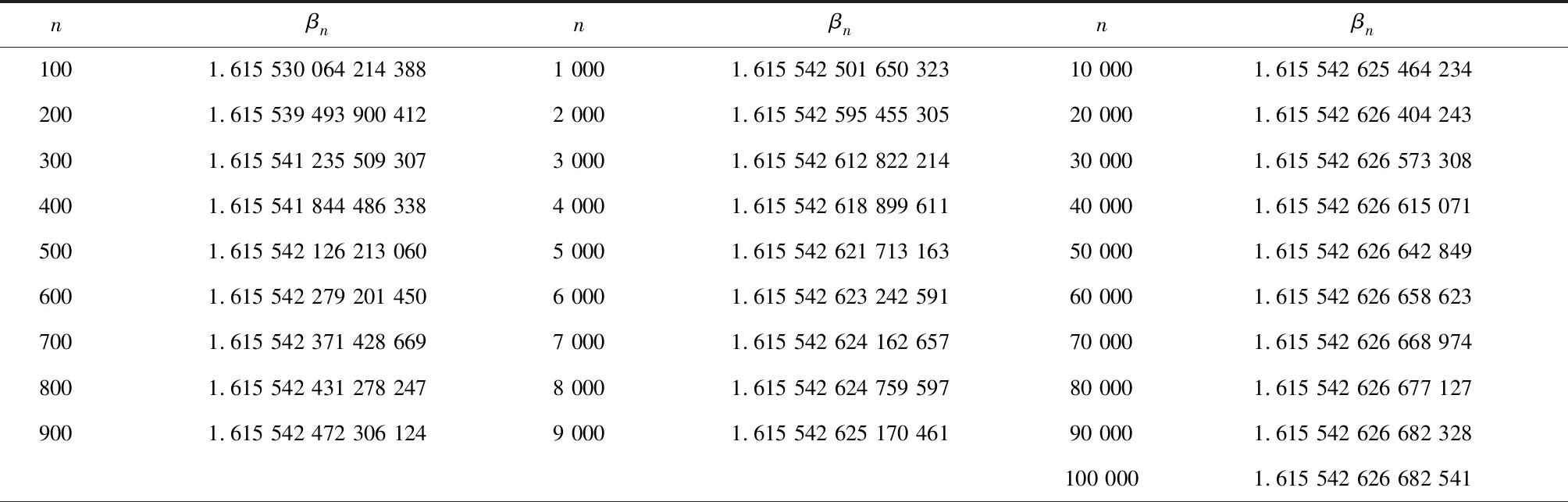
表1 二维氯化铯结构的埃夫琴法的马德隆常数