两类特殊亚循环群之间的同态数量
任小强, 高百俊
(伊犁师范大学 数学与统计学院, 应用数学研究所, 新疆 伊宁 835000)
0 引 言
目前,关于Sylow子群的研究已有很多结果,其中: 黄本文[1]利用可解群的性质, 通过群的扩张理论给出了Sylowp-子群皆循环的10pn阶群的构造; 吉晓娟等[2]结合图的性质对Sylowp-子群皆循环的10pn(p>5)阶群进行了分类, 更正了文献[1]结论的错误, 确定了这类群共有5种同构分类, 并进一步研究了该群的非交换图; 陈松良[3-4]先后给出了两类Sylow子群循环的有限群的同构分类.另一方面, 文献[5-7]通过计算有限群之间的同态数量研究了有限群的结构; Asai和Yoshida[8]发现前人的结论中少有关于两个有限群之间同态数量的猜想, 于是提出了一个有关群同态数量的猜想; 文献[9-11]验证了一些特殊的有限群满足Asai和Yoshida猜想; 张良等[12]提出了一类m阶循环群被4阶循环群扩张的亚循环群, 并计算了这类群之间的同态数量.本文在上述研究的基础上, 以文献[2]中第一种同构分类形式为研究对象, 讨论这类群的元素特征, 考察其与文献[12]中提出的这类m阶循环群被4阶循环群扩张的亚循环群之间的同态以及同态数量, 并验证这两类群也满足Asai和Yoshida猜想.
为方便叙述, 先给出这两类群的结构:

1 预备知识
引理1设H=〈a,b〉, 其中a10=1=bpn,a-1ba=br,r≢1(modpn),r5≡1(modpn),p≡1(mod 5), 这里p是大于5的素数, 则:
1) 〈a〉∩〈b〉=1;
2) 满足rk≡1(modpn)的最小正整数k=5;
3)bja=abjr,bjai=aibjri, 其中0≤i<10, 0≤j 证明: 1) 显然成立. 2) 设使得rk≡1(modpn)成立的正整数k的最小值为m, 已知r≢1(modpn),r5≡1(modpn),rm≡1(modpn), 由费马定理的性质可知m|5且m≠1.又因为5是素数, 所以m=5.故2)成立. 3) 由于a-1ba=br, 因此ba=abr, 即(a-1ba)j=a-1bja=(br)j, 进而得 bja=abjr,bjai=(bja)ai-1=(abjr)ai-1=a(bjra)ai-2=a2bjr2ai-2=…=aibjri. 故3)成立. 引理2H记号如上, 则: 1)o(a5)=2; 3)o(a5bj)=[2,o(bj)], 且a5是H的中心元, 其中1≤j 4)o(aibj)=5, 其中(pn,ri-1)=1, 且i=2,4,6,8, 0≤j 5)o(aibj)=10, 其中(pn,ri-1)=1, 且i=1,3,7,9, 0≤j 证明: 1),2)由有限群元素阶的性质易得结论. 3) 由H的定义得pn|j(r5-1), 于是bjr5=bj.由引理1中3)得bja5=a5bj.因此, 由元素阶的性质得o(a5bj)=[2,o(bj)].任取akbl∈H, 其中0≤k<10, 0≤l 4) 设o(aibj)=5, 其中0 r5i-1=(r4i+r3i+r2i+ri+1)(ri-1); 当(pn,ri-1)=1时, 有r4i+r3i+r2i+ri+1≡0(modpn), 进而当i=2,4,6,8时, (aibj)5=a5ibj(r4i+r3i+r2i+ri+1)=1; 当i=1,3,5,7,9时, (aibj)5=a5ibj(r4i+r3i+r2i+ri+1)=a5i=1, 无解, 故4)成立. 5) 设o(aibj)=10, 其中0 (aibj)10=a10ibj(r9i+r8i+…+ri+1)=bj(r9i+r8i+…+ri+1); 由引理1中2)及欧拉-费马定理可得r10i≡1(modpn), 即r10i-1≡0(modpn).又 r10i-1=(r9i+r8i+…+ri+1)(ri-1), 当(pn,ri-1)=1时, 由3)和4)可知,i只能取1,3,7,9, 故5)成立. 引理3H记号如上, 若(pn,r-1)=1, 则H′=〈b|bpn=1〉. 证明: 任取aibj,asbt∈H, 由引理1中3)得 又(pn,r-1)=1, 易得o(br-1)=pn, 所以br-1是群〈b〉的生成元, 即 H′=〈br-1|bpn=1〉=〈b|bpn=1〉. 证明: 根据群的构成, 结论显然成立. 2)o(xβy2)=[o(xβ),2], 其中0≤β 3)o(xβy)=o(xβy3)=4, 其中0≤β 定理1设m是大于2的奇数,p是大于5的素数, 则|Hom (Gm,H)|=2. 证明: 设θ∈Hom(Gm,H), 由于xm=1=y4, 则 (xm)θ=(xθ)m=1, (y4)θ=(yθ)4=1, 从而o(xθ)|(m,10pn),o(yθ)|2. 当p|m时, 有o(xθ)|5pα或o(xθ)|pα, 0<α≤n.于是由引理2可知, xθ∈{1}∪{aibj|i=2,4,6,8, 0≤j yθ∈{1}∪{a5}.当p⫮m时, 有o(xθ)|5或o(xθ)|1.于是由引理2可知 xθ∈{1}∪{aibj|i=2,4,6,8, 0≤j yθ∈{1}∪ {a5}.因此, 当p|m时, 先令xθ=1, 若yθ=1, 则θ显然为平凡同态.此时, 群同态θ只有1种选择;若yθ=a5, 则任取xsyt∈Gm, 规定(xsyt)θ=(a5)t, 其中0≤s (xs1yt1xs2yt2)θ=(xs1-s2yt1+t2)θ=(a5)t1+t2=(xs1yt1)θ(xs2yt2)θ 成立, 当t1为偶数时, 有 (xs1yt1xs2yt2)θ=(xs1+s2yt1+t2)θ=(a5)t1+t2=(xs1yt1)θ(xs2yt2)θ 成立, 于是(xs1yt1xs2yt2)θ=(xs1yt1)θ(xs2yt2)θ, 即θ为群同态.此时, 群同态θ只有1种选择. 再令xθ=bj,o(bj)|pα, 0 最后, 令xθ=aibj,i=2,4,6,8, 0≤j 当p⫮m时, 与前述同理可知, 当xθ=1时, 无论yθ=1还是yθ=a5, 都有θ是群同态且群同态θ都只有1种选择;当xθ=aibj,i=2,4,6,8, 0≤j 综上可得, |Hom(Gm,H)|=2. 定理2设m是不小于2的偶数,p是大于5的素数, 则|Hom(Gm,H)|=4. 证明: 设θ∈Hom(Gm,H), 由定理1可知o(xθ)|(m,10pn),o(yθ)|2. 当p|m时, 有o(xθ)|10pα或o(xθ)|2pα, 0<α≤n.由引理2可知, yθ∈{1}∪{a5}.当p⫮m时, 有o(xθ)|10或o(xθ)|2.由引理2可知, yθ∈{1}∪{a5}. 于是, 当p|m时, 首先令xθ=1, 若yθ=1, 则由定理1知θ是群同态, 且群同态θ有1种选择;若yθ=a5, 则由定理1知θ是群同态且群同态θ有1种选择. 其次, 令xθ=a5, 若yθ=1, 则任取xsyt∈Gm, 规定(xsyt)θ=(a5)s, 其中0≤s (xs1yt1xs2yt2)θ=(xs1-s2yt1+t2)θ=(a5)s1-s2, (xs1yt1)θ(xs2yt2)θ=(a5)s1+s2, (a5)2s2=1, 即 (xs1yt1xs2yt2)θ=(xs1yt1)θ(xs2yt2)θ. (1) 当t1为偶数时, 有 (xs1yt1xs2yt2)θ=(xs1+s2yt1+t2)θ=(a5)s1+s2=(xs1yt1)θ(xs2yt2)θ 成立, 于是式(1)成立, 即θ为群同态.此时, 群同态θ有1种选择.若yθ=a5, 则任取xsyt∈Gm, 规定(xsyt)θ=(a5)s+t, 其中0≤s (xs1yt1xs2yt2)θ=(xs1-s2yt1+t2)θ=(a5)s1-s2(a5)t1+t2, (xs1yt1)θ(xs2yt2)θ=(a5)s1+t1(a5)s2+t2, (a5)2s2=1, 即式(1)成立.当t1为偶数时, 有 (xs1yt1xs2yt2)θ=(xs1+s2yt1+t2)θ=(a5)s1+s2(a5)t1+t2=(xs1yt1)θ(xs2yt2)θ 成立, 于是式(1)成立.即θ为群同态.此时, 群同态θ只有1种选择. 再次, 令xθ=aibj,i=1,3,7,9, 0≤j 最后, 令xθ=a5bj,o(a5bj)|2pα, 0 当p⫮m时, 与前述同理, 首先令xθ=1或令xθ=a5时, 无论yθ=1还是yθ=a5, 都有θ是群同态且群同态θ都只有1种选择;其次, 令xθ=aibj,i=2,4,6,8, 0≤j 综上可得, |Hom(Gm,H)|=4. 定理3设m是大于2的奇数,p是大于5的素数, 则: 1) 当5|m时, |Hom(H,Gm)|=10ph, 这里ph=(pα,r-1)且0≤α≤n; 2) 当5⫮m时, |Hom(H,Gm)|=2ph, 这里ph=(pα,r-1)且0≤α≤n. 证明: 设θ∈Hom(H,Gm), 由于a10=1=bpn, 则 (a10)θ=(aθ)10=1, (bpn)θ=(bθ)pn=1, 从而o(aθ)|(10,4m),o(bθ)|(pn,m). 当5|m时, 有o(aθ)|10,o(bθ)|pα, 这里0≤α≤n.若aθ=xβ, 则 (aθ)m=(xβ)m=(xm)β=1, 于是o(aθ)|m, 从而o(aθ)|5;若aθ=xβy2, 则(aθ)2m=(xβy2)2m=1, 于是o(aθ)|2m, 从而o(aθ)|10.于是由引理5可知 当5⫮m时, 有o(aθ)|2,o(bθ)|pα, 这里0≤α≤n.由引理5可知 aθ∈{1}∪{y2},bθ∈{xβ|o(xβ)|pα, 0≤β 因此, 当5|m时, 首先令aθ=xi,o(xi)|5, 0≤i as1-s2=bt2-t1∈〈a〉∩〈b〉=1, 于是10|(s1-s2)且pn|(t2-t1), 由已知条件可知(xi)s1(xβ)t1=(xi)s2(xβ)t2, 即(as1bt1)θ=(as2bt2)θ, 因此θ为映射.又 由已知ph=(pα,r-1), 则ph|(r-1), 从而ph|t1(rs2-1), 而o(xβ)|ph, 所以o(xβ)|t1(rs2-1), 于是(xβ)t1(rs2-1)=1, 即(xβ)t1rs2+t2=(xβ)t1+t2, 从而 (xi)s1+s2(xβ)t1rs2+t2=(xi)s1+s2(xβ)t1+t2, 其次, 令aθ=xiy2,o(xiy2)|10, 0≤i as1-s2=bt2-t1∈〈a〉∩〈b〉=1, 于是10|(s1-s2)且pn|(t2-t1), 由已知条件可知(xiy2)s1(xβ)t1=(xiy2)s2(xβ)t2, 即(as1bt1)θ=(as2bt2)θ, 因此θ为映射.又 (as1bt1as2bt2)θ=(as1+s2bt1rs2+t2)θ=(xiy2)s1+s2(xβ)t1rs2+t2, (as1bt1)θ(as2bt2)θ=(xiy2)s1(xβ)t1(xiy2)s2(xβ)t2=(xiy2)s1+s2(xβ)t1+t2, 由已知ph=(pα,r-1), 则ph|(r-1), 从而ph|t1(rs2-1), 而o(xβ)|ph, 所以o(xβ)|t1(rs2-1), 于是(xβ)t1(rs2-1)=1, 即 (xiy2)s1+s2(xβ)t1rs2+t2=(xiy2)s1+s2(xβ)t1+t2, 因此, 当5|m时, |Hom(H,Gm)|=10ph. 当5⫮m时, 与前述类似可知, 无论令aθ=1还是令aθ=y2, 当bθ=xβ,o(xβ)|ph,ph=(pα,r-1), 0≤h≤α, 0≤β 定理4设m是不小于2的偶数,p是大于5的素数, 则: 1) 当5|m时, |Hom(H,Gm)|=20ph, 这里ph=(pα,r-1)且0≤α≤n; 2) 当5⫮m时, |Hom(H,Gm)|=4ph, 这里ph=(pα,r-1)且0≤α≤n. 证明: 设θ∈Hom(H,Gm), 由于a10=1=bpn, 则 (a10)θ=(aθ)10=1, (bpn)θ=(bθ)pn=1, 从而o(aθ)|(10,4m),o(bθ)|(pn,m). 当5|m时, 有o(aθ)|10,o(bθ)|pα, 这里0≤α≤n.若aθ=xβ, 则(aθ)m=(xβ)m=(xm)β=1, 于是o(aθ)|m, 从而o(aθ)|10;若aθ=xβy2, 则(aθ)2m=(xβy2)2m=1, 于是o(aθ)|2m, 从而o(aθ)|10.进而由引理5可知 当5⫮m时, 有o(aθ)|2,o(bθ)|pα, 这里0≤α≤n.由引理5可知 当5⫮m时, 与前述类似可知, 无论令aθ=xβ,o(xβ)|2, 0≤β Asai和Yoshida猜想[8]: 设A,G是两个有限群,A′是A的换位子群, 则 |Hom(A,G)|≡0(mod(|A/A′|,|G|)). 下证群Gm和群H之间的同态个数满足Asai和Yoshida猜想. 推论1设m≥2为正整数,p>5为素数, 则 推论2设m≥2为正整数,p>5为素数, 则 |Hom(H,Gm)|≡0(mod(|H/H′|,|Gm|)). 证明: 因为|H/H′|=10, 故|Gm|=4m.当5|m时, (|H/H′|,|Gm|)=10;当5⫮m时, (|H/H′|,|Gm|)=2.由定理3和定理4知结论成立, 即群H到群Gm的同态个数满足Asai和Yoshida猜想.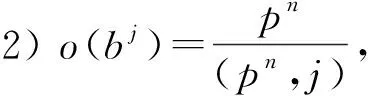


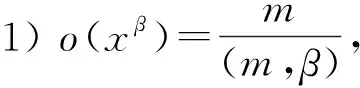


2 主要结果

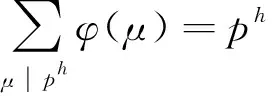
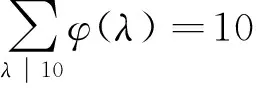
3 应 用

