利用压电阵列设计直升机桨叶的模态传感器*
王渊德, 毛崎波, 黄仕卓
(南昌航空大学 飞行器工程学院,江西 南昌 330063)
0 引 言
阵列式压电模态传感器设计的基本思想是在结构表面布置一组形状相同的压电传感元件,通过为每个压电元件设计不同的加权系数,使这组压电传感阵列加权后的输出等于目标阶的模态坐标。阵列式压电模态传感器的设计方法[10~12](如模态方法、伪逆方法以及曲率模态方法等)相继被提出和实验验证。其中,将曲率模态作为加权系数的设计方法的关键是获取结构的曲率模态。利用传统的加速度计进行实验模态分析可获得结构的模态振型;再利用线性插值、中心二次差分等数学方法来对模态振型进行处理以获得结构的曲率模态。但数值计算方法在二阶求导时,实验数据中的干扰误差会被放大,从而导致曲率模态失真。Wang B T[13]提出了利用压电阵列直接测量结构曲率模态的可行性,避免了在对结构模态进行二阶求导时的干扰放大问题。
为验证阵列式压电模态传感器在实际应用中的可靠性,以直升机桨叶为例,将锆钛酸铅压电陶瓷(Pb-based lanthanum-doped zirconate titanates piezoceramics,PZT)作为压电传感元件,利用将曲率模态作为加权系数的方法设计模态传感器。同时,利用激光多普勒测振仪测量结构的模态振型和数值研究的方法得到结构的曲率模态,进行对比研究。测试了利用压电阵列为桨叶设计模态传感器的可行性,为压电智能结构的减振在直升机桨叶上的应用提供了验证思路。
1 基本理论
直升机桨叶可简化为一悬臂梁。现设有一悬臂梁,在梁上均匀布置n片大小相等的圆形PZT。根据阵列式压电模态传感器的设计方法,为得到结构第m阶模态坐标Am,需要为每片PZT设计相应的加权系数,如图1所示。假设第k片PZT的输出频响函数为Hk(ω),则模态传感器的输出可表示为

图1 阵列式压电模态传感器原理
(1)
式中Wkm为目标阶模态坐标为Am时第k片PZT的加权系数。
由Wang B T[13]的研究可知,设在xf处施加一外力F,仅考虑前M阶模态,则第k片PZT输出电荷Qk(ω)与激励力F(ω)之间的频响输出可表示为

(2)
其中
2016年11月,全国妇联、教育部等九部委在《关于指导推进家庭教育的五年规划(2016—2020年)》明确提出了五年内在全国普及家长学校的工作目标——城市要达到90%,农村要达到80%,让有限优质教育资源服务更多学校和社区。
(3)
式中e31为压电常数;hp为圆形PZT的厚度;L,ρ,b和h分别为梁的长度、密度、截面宽度和厚度;bp(x)为PZT在梁上的有效宽度;Am为模态坐标,φm(x)为模态振型。
当使用大小相同的圆形PZT作为压电传感器时,式(2)可进一步简化为
(4)
式中bp(常数)为PZT的等效宽度,xk为第k片PZT的位置,r为圆形PZT的半径。
将式(4)代入式(1),并根据拉格朗日中值定理,则该压电传感器阵列的加权后的输出可表示为
(5)
式中xξ∈(xk-r,xk+r)。
Wang B T[14]进一步指出,对于具有经典边界(固支、简直、自由端等)的结构,其曲率模态具有正交性,离散化后的曲率模态仍具有正交性,即
(6)
由式(5)、式(6)可知,若将结构第m阶离散的曲率模态φ″m(xk)作为PZT阵列的加权系数,则加权后的输出可表示为
(7)
将式(3)代入式(2),第k片PZT的输出频响函数可重新表示为
(8)
由式(8)可知,当激励力的位置xf固定(即φm(xf)为常数)时,利用布置在梁上的PZT阵列输出的频响函数进行实验模态分析得到的模态振型,即为该结构离散的曲率模态。
2 实验研究
为研究将曲率模态作为加权系数为直升机桨叶设计阵列式压电模态传感器的方法在实际应用中的可靠性。对一长970 mm的复合材料直升机桨叶(如图2)进行实验研究。在桨叶下表面最大厚度处均匀布置10片PZT,每片PZT的间隔为100 mm,第1片PZT到固定端的距离为45 mm。

图2 实验用直升机桨叶
实验所用的PZT如图3所示。将一质量为56 g的小型惯性作动器固定在第2片PZT背面(xf为145 mm)处作为激励。
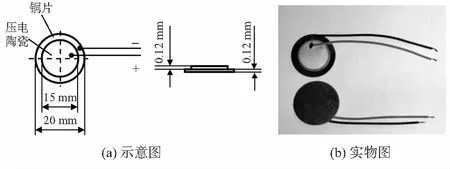
图3 实验用PZT示意图和实物图
实验中,采用具有24通道的COINV动态信号分析仪对输入到作动器的激励电压和PZT的输出电压进行采集,并分析得到系统输出与PZT输出间的频响函数H(ω)。再将测得的信号导入DASP—V10模态分析软件,以获取该桨叶离散的曲率模态。利用以上获得的频响函数和离散曲率模态,根据式(1)则可获得所需阶数的模态坐标。实验同时使用PSV—500多普勒激光测振仪对桨叶进行测量,并分析得到机翼的模态振型。实验装置如图4所示。

图4 实验设备与装置
表1为PZT和激光多普勒测振仪测得的桨叶前5阶固有频率。由表1可看出,PZT对直升机桨叶固有频率的测量结果和激光多普勒测振仪的测量结果基本一致。

表1 直升机桨叶前5阶固有频率
实验中,PZT对桨叶的第1阶振动感知不明显,但直升机桨叶在工作时振动频率都较高,故在本文实验中只为该直升机桨叶设计第2阶~第5阶的模态传感器。图5给出了10片PZT输出的频率响应函数。频率响应函数在共振点处的峰值清晰,说明PZT能很好地测量桨叶的模态信息。图6为实验模态分析的第2阶~第5阶模态置信矩阵。由图6可知,置信矩阵对角线的值为1,远大于非对角线的值,曲率模态具有很好的正交性,模态分析效果良好。

图5 激励力与10片PZT输出电压之间的频率响应函数曲线

图6 曲率模态置信矩阵直方图(MAC)
为研究通过数值方法求曲率模态设计模态传感器的实际应用。实验中,激光多普勒测振仪设置21个扫描点,沿PZT阵列的中轴线均匀分布在桨叶上。图7为激光测振仪测量得到的桨叶第2阶~第5阶的模态振型。将离散模态振型进行3次样条插值,并对插值后的模态振型求2阶导数,得到结构的曲率模态。在计算得到的曲率模态曲线上,取PZT中心所在位置的值,组成与PZT实测值相对应的离散曲率模态。图8给出了分别利用PZT和多普勒激光测振仪测量得到的离散曲率模态直方图。
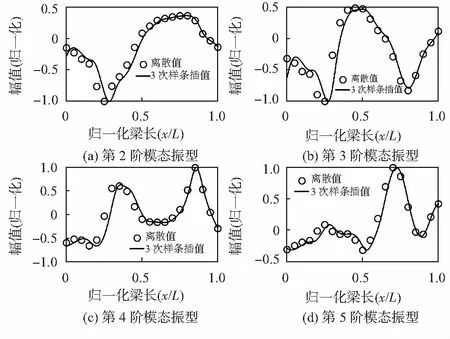
图7 激光测振仪测得的桨叶第2阶~第5阶模态振型

图8 桨叶曲率模态直方图
图9给出了分别利用激光测振仪和PZT测得的曲率模态作为加权系数时,第2阶~第5阶模态传感器的归一化输出,以及理论的模态坐标(式(3))。由图9可知,利用PZT阵列设计的模态传感器准确输出了对应阶的模态坐标。虽然非目标阶固有频率处仍存在一定的峰值,其产生的原因主要是实验中桨叶的边界条件与在进行实验模态分析时建立的结构的边界条件存在一定误差,这导致实验模态分析得到的曲率模态与理论曲率模态之间存在一定误差。另外,桨叶上的PZT并不是严格的均匀粘贴,存在一定的位置偏差。同时,环境噪声也会对其测量造成一定的干扰。但该模态传感器输出的非目标阶固有频率处峰值远小于目标阶固有频率处峰值,阵列式模态传感器的滤波效果良好。

图9 用于直升机桨叶模态传感器实验结果
在利用激光测振仪设计模态传感器时,由于桨叶并不是理想的固定状态,存在一个刚体自由度,从而影响了激光测振仪测量结构振型的幅值。同时,由于桨叶截面为非对称截面,惯性力很难通过截面形心并与主惯性轴重合,直升机桨叶存在扭转振动,当把桨叶简化为一维结构并通过激光多普勒测振仪获取其模态振型时,扭转振动所引起的位移对模态振型的提取有一定的干扰,如图7所示。当对上述获得的模态振型进行中心二次差分求曲率模态,在数值计算过程中,该误差被进一步放大,从而导致计算得到的曲率模态失真。显然,由图9可知,将失真的曲率模态作为加权系数设计的模态传感器并不能输出结构的模态坐标,或输出的非目标阶峰值很大(如图9第4阶模态滤波结果)。而利用PZT测量并通过实验模态分析设计阵列式模态传感器时,不需要考虑桨叶的具体振动形式,以及对边界条件和环境条件没有苛刻的要求。
3 结 论
利用PZT阵列设计直升机桨叶的模态传感器,并运用激光多普勒测振仪进行了对比研究。利用PZT阵列测量桨叶的振动并进行实验模态分析得到结构的曲率模态。同时,利用激光多普勒测振仪测得桨叶的模态振型并通过中心二次差分获得桨叶的曲率模态。分别将上述2种曲率模态作为加权系数设计模态传感器。实验结果表明:PZT可用于直升机桨叶的阵列式压电模态传感器设计。与利用激光测振仪相比,利用PZT阵列设计模态传感器的方法不需要复杂的数值计算,且抗干扰能力强,鲁棒性好。同时,由于PZT传感器具有质量轻、工程造价低、机电转换效率高等优点,将PZT应用于压电智能结构的设计具有很高可行性。

