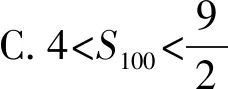让数列放缩落地生根
——对2022年浙江省数学高考第10题的研究
董昊雷
(镇海中学,浙江 宁波 315200)
深度学习是一种新的教学模式.与浅层次的学习相比,它更注重知识的本质,提倡创新的建构,更能培养高阶的思维、发展学生的数学核心素养.在数学解题教学中,不能只是低层次地重复训练,而是要达到“解一题,懂一法,会一类,通一片”的目标[1].下面,笔者以2022年浙江省数学高考第10题为例,谈谈如何在解题教学中实施深度学习.
1 高考题的引入:深度学习的准备
1.1 问题呈现
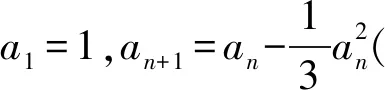
( )
(2022年浙江省数学高考试题第10题)

图1
1.2 解法呈现
根据以往经验,由递推关系确定通项,可以用蛛网图定性分析(如图1),得到an的范围:0 由上述分析可知0 (1) 累加得 即 亦即 100a100<3, 右侧不等式得证. 所以 即 故选B. 作为教师,一方面我们需要思考如何处理高考试题才能充分发挥其价值;另一方面我们还要思考如何让学生从被动学习到主动学习.如果单纯地将解题过程和结果灌输给学生,再通过大量的练习、变式等让学生进行机械地训练,这样的被动学习效果事倍功半.教师应让学生在解决问题的过程中把遇到的难点挖掘出来,并寻找难点背后的本质,这样的主动学习才能事半功倍.而问题链的引入可以较好地解决这个问题,正所谓“学习来源于思考而思考又由问题产生”.问题链不仅可以作为脚手架帮助学生突破难点,从而获得较高水平的数学知识,还能发散学生的思维,构建、完善认知体系.与此同时,学生通过问题链提炼本质的过程中还能获得数学方法、领悟数学思想、发展核心素养. 根据上述的指导思想,本文设计的问题来源于对高考试题的分析,而这些设计的问题既可以作为脚手架帮助学生逐个突破难点,又可以通过深入剖析挖掘此高考题的本质.具体来说本文设计的问题如下: 1)能否将此问题与教材中的等差、等比数列进行联系? 下面将对这3个问题逐个进行分析并给出解答. 问题1)的目的是寻找高考题的落脚点,挖掘高考题背后的主要知识体系.教师在解题教学中不应另起炉灶“发明”新的结论“创造”新的方法[2],接着通过大量的练习或变式强化这一方法,这样做与深度学习背道而驰.深度学习是让学生联系已有的知识,尤其是课本中的知识,利用已有的知识储备解决一些具有挑战性的问题,让学生明白高考题来源于课本又高于课本.而例1就可以利用课本中等差数列的定义与性质解决,具体思路如下. 当an+1-an=d(其中d为常数)时,数列{an}为等差数列,同时可以用累加法得到通项公式an=a1+(n-1)d.若d是一个变化的量dn,则{an}就不是等差数列了,姑且把它叫做“类等差数列”.直接对“类等差数列”累加求和是没有意义的,但如果限制dn的范围,再累加求和即可以得到an的范围,问题就会有所突破.例1将递推式取倒数变形得到 从而 设置问题2)不仅提出了解决例1的难点,更是通过深入剖析问题得到了解决一类题的方法模型,即该问题的范式,这就是所谓的“会一类,通一片”.在教学中,我们会发现这一步的代入限制范围并不容易.若将此步骤直接告诉学生,让学生模仿并记住,那就是所谓的浅层次学习.深度学习则是让学生在剖析“为什么”的过程中发现“利用an的范围限制dn的范围,从而累加进一步缩小an的范围,再限制dn的范围,缩小an的范围……”.这一过程,图示如下: 上述的方法模型可以让学生探索并自行归纳.此类范式不仅可以用于“类等差”数列,也可以用于“类等比”数列. 设置问题3)的目的是希望通过进一步的研究,对此问题有一个更深入的认识,同时也可以让学有余力的学生通过深入研究后得到更高阶的知识,从更高的视角审视问题的本质.在教学中,我们发现递推关系的变形有很多种,如何选择就显得至关重要.代数的变形并不是凭经验、凭记忆的,而是有它的理论依据.斯托尔茨定理就告诉我们“该选择哪一种变形方式,朝着哪个目标变形”,同时这样的变形也为后续的放缩做了铺垫,因此这是一个较高层次的整体把握. 斯托尔茨定理: ①{bn}严格单调递增; 其中L可为有限数,也可为+∞,-∞. ①{bn}严格单调递减且趋于0; 其中L可为有限数,也可为+∞,-∞. 此定理可以用于数列阶的估计.回到例1,由于{an}单调递减,且an→0,设an~αnβ,那么 从而 即 深度不应局限于单一的数学知识与技巧,应该让学生从“知道如何思考”到“学会思维”,也就是说要把握好深度学习的基本途径,让深度学习变成一种学习的能力.作为教师,我们不但要联想和本题相关联的模型,对比其相同点和不同点,还要思考能否应用或迁移所学的知识,将其用于其他的有挑战性的问题中.我们知道深度学习能做到“研一题,通一类”,也就是说本例的解决不仅有助于解决此类“类等差数列”或“类等比数列”的问题,还能作为一种活动经验的积累去研究其他有价值的问题. 有了研究例1的经验,可以较快地解决例2: ( ) 解由题意可得 因为 即 从而 于是 进而 故选A. 同时我们发现如果对例1有充分的研究,那么例2也就不难解决.因此,这两个例题都能作为较好的载体帮助学生体会其中的思想方法,同时在分析问题、研究问题、解决问题的过程中发展数学核心素养. 最后从教学评价来看,笔者通过深入讲解例2,学生在解决例1时就非常得心应手,据统计有一半以上的学生能较顺利地解决例1.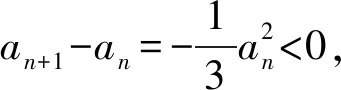
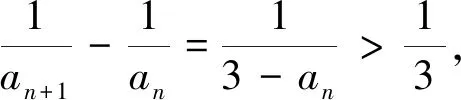




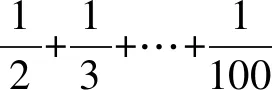

2 问题链的构建:深度学习的实践
2.1 回归思维起点

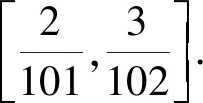

2.2 获得方法模型

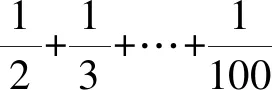
2.3 探寻问题本质








3 多维度的理解:深度学习的应用