重在纠错 引入变式 提升思维 促进反思——以高三数学试卷讲评课的教学实践为例

王 芬

(龙游县第二高级中学,浙江 龙游 324400)

进入高三备考阶段，面对着种目繁多的考试，试卷讲评课显得尤为重要.一堂高效优质的试卷讲评课不仅能帮助教师及时地做好查漏补缺工作，而且还能提高学生的成绩，进而提升学生的数学思维.但是，由于目前不少教师对试卷讲评的意义了解得不够，讲评时存在着毫无侧重点之分、逐题顺次讲解、重讲轻练等问题，导致课堂效率低下，学生成绩进步不明显.因此，如何提升高三数学试卷讲评课的有效性值得探讨.笔者结合自己的教学实践，谈谈个人的一点教学感悟.

1 善于暴露学生的典型错误

心理学家盖耶认为：“谁不思考尝试错误、不鼓励学生犯错误，就将错过最有效果的教学时间.”学生学习的过程本来就是一个不断尝试错误的过程，教师要让学生在解决问题的过程中暴露错误和思维过程，进而帮助学生审视错误、纠正错误，并有针对性地预防错误.因此，学生在考试中出现的错误是一种宝贵的教学资源，若能将这种教学资源运用到课堂中，则会给试卷讲评课带来新的活力.

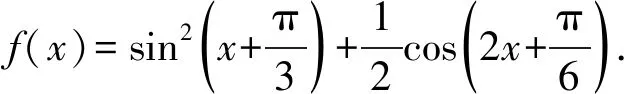
2)求函数y=f(x)的最小正周期及单调递增区间.

此试题的分值为14分，属基础试题，难度不大.不过根据考试成绩反馈的数据来看，平均分只有6分左右，正确率不高.于是笔者把一些典型的错误解答在试卷讲评课上进行讲解，揭示学生的错误思想，引导和帮助学生纠正错误，加深学生对错误的认识.对于第1)小题，有如下错解：

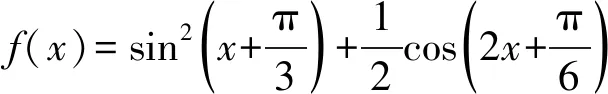
所以

错解3解答过程中的第3步出现了漏抄的错误(略).

因为

所以

综上可看出，该题的难点在于化简三角函数.其实正确的化简过程很简单:平方降幂之后灵活地运用诱导公式就可以化成同角三角函数，利用三角函数辅助角公式合为一个函数.具体化简过程如下：

解因为

所以

因此，教师在讲评中要重视学生考试过程中出现的错误，帮助学生深刻剖析错因，避免今后再发生类似的错误.这种试卷讲评模式是有一定价值的.

2 善于激发学生的灵动思维

面临高考的压力和高三紧张的学习任务，教师要想方设法地提高试卷讲评课的效率，通过选取典型试题加以精讲精练，探讨并发现基本规律，锻炼解题技巧，以开阔学生的视野，并获得举一反三的效果.因此，在试卷讲评课中，教师要引导学生仔细审题，认真思考，学会借“题”发挥，让讲评效果真正深入“生”心.

2.1 一题多解，培养灵动思维的同时注重通法

一题多解是对同一道题，从不同的角度去观察、分析，全方位地思考问题，运用不同的知识获得多种不同的解法，最终达到殊途同归的目的[1].

即

解得

从而

故

tanα=3.

cosα≠0,

两边平方,得 9sin2α+6sinαcosα+cos2α=10，

即

分子分母同除以cos2α，得

整理得

tan2α-6tanα+9=0，

即

(tanα-3)2=0，

故

tanα=3.

故

tanα=3.

解法4构造对偶式3sinα-cosα=m，联立

得

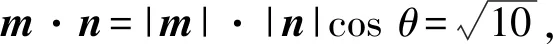
所以

cosθ=1，

即m与n共线.由向量共线的充要条件可得

3·cosα-1·sinα=0，

故

tanα=3.

sin(α+φ)=1,

即

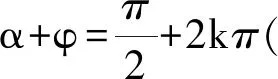
从而

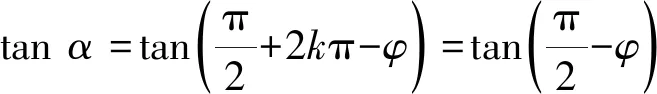
通过一题多解的教学，帮助学生寻找一种最适合自己的解法(即通法).比如例2虽有多种解法，但通法一般也就一两种.比如解法1和解法2就是通法，而解法3～6对特殊技巧的要求比较高，忽视了学生的认知水平.因此，笔者认为注重通性通法的教学很关键，有助于提高学生的解题能力.

2.2 一题多变，培养发散思维的同时抓住本质

一题多变是在原题的基础上改变条件或结论，形成新的题目，在不断变形的过程中，让学生关注前后联系，抓住问题的本质，努力实现“立足一道题，解决一类题”的目的.

图1

解决此类题的方法主要有以下3种：1)等和线；2)坐标法；3)数量积[2].选择坐标法来解决此类题过程复杂，耗时较长.由于此类题基本以小题的形式出现，因此可以考虑选择更简便的方法来解决.选择数量积来解决存在一定难度，而且综合性较强，学生不容易想到，因此对于例3来说等和线是最合适的方法.

图2 图3

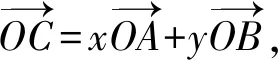
该定理是求系数和的范围：若直线l与点O在直线AB的异侧，则l离AB越远，系数和越大；若直线l与点O在直线AB的同侧，则l离AB越远，系数和越小.

例3的解法如下：

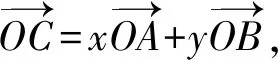
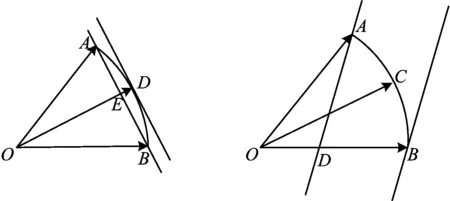
图4 图5

变式1解答如下：

变式2解答如下：

图6 图7

变式3解答如下：

通过一题多变的教学，可以给出一系列变式题，使学生的思维时刻处在一种活跃的状态中，比如变式1改变结论，变式2改变条件，变式3深化结论，但是不管怎样变化，解决此类题的关键是要抓住问题的本质，学会从变中总结解题技巧，从变中找到规律，从变中发现“不变”，从而提高学生解决问题的能力.

2.3 多题一解，增强归纳能力的同时提炼共性

多题一解是针对不同的问题，在解决的同一步骤中采用了相同的方法或相近的方式[3].通过归纳分析可以提炼共性，发现该类问题的本质，并以此培养学生的解题技巧，从而获得举一反三、触类旁通的效果.

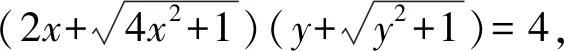
化简可得

因为mn=4,所以

例5已知x,y∈R且满足4x+y+2xy+1=0，则x2+y2+x+4y的最小值为______.

解由4x+y+2x+1=0,得

(2x+1)(y+2)=1，

因为mn=1,所以

例6已知实数x,y满足x2-2xy-3y2=1，则x2+y2的最小值为

( )

解由x2-2xy-3y2=1,得

(x-3y)(x+y)=1，

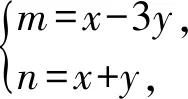
因为mn=1,所以

故选B.

通过多题一解的教学，可以达到解决一道题就能懂一类题的效果.比如例4借助二元方程考查二元最值的问题，利用换元法将其简化就能顺利解决，此方法在例5和例6中同样适用，从而培养学生思维的深刻性，提高学生的归纳能力.

3 善于发挥学生的主体地位

新课程理念倡导课堂教学以学生为主体、教师为主导，同时又强调学生个性发展.因此在试卷讲评课中，教师应尽量给学生创造条件，鼓励学生主动参与到课堂中来，从只有教师讲的课堂转变为师生共同讲的课堂，这样做既听取了学生的见解，又充分调动了学生的积极性，更重要的是教师既传授了知识，又了解到学生的思维倾向.

例7已知a,b∈R，若函数f(x)=aex-bx存在两个零点x1,x2，且x2>x1>0，则下列结论可能成立的是

( )

A.ae>b>0 B.0>ae>b

C.b>0>ae D.ae>0>b

解法1(常规方法：利用函数的单调性求解)由已知f(x)=aex-bx,得

f′(x)=aex-b.

1)当a<0,b>0时，f′(x)<0，则f(x)在(0,+∞)上单调递减，不满足题意，故舍去.

2)当a>0,b<0时，f′(x)>0，则f(x)在(0,+∞)上单调递增，不满足题意，故舍去.

在试卷讲评过程中，除了常规解法外，教师还可以适当留点时间让学生自主思考或小组讨论，听听他们不同的解题思路，相信会使学生们得到更大的收获.另有3种解法由生1～3提供：

生3(解法4)：此题是选择题，还可以取特殊值代入法求解，比如选项A可以取a=b=1，选项B可以取a=-1,b=-e2，选项C可以取a=-1,b=1，选项D可以取a=1,b=-1.由这个思路可以得出答案为B.

最终在学生积极发言的课堂模式下，师生共同合作，总结归纳出4种不同的解题方法，如此很好地扩大了学生的思维宽度，既充分调动了学生的学习兴趣，又培养了学生的逻辑思维和应试能力.

4 善于进行课后反思

荷兰的杰出数学教育家佛赖登塔尔认为：“反思是数学思想活动的核心和动力.”上完一堂试卷讲评课，教师要特别重视课后反思和总结，通过剖析课堂中的优缺点，并加以仔细研究，在不断提升自己教学水平的同时，又提高了学生的数学成绩.

如例7是含有双参数的函数零点问题，也是近年来浙江省高考中的热点考题，此类题型着重考查函数、导数、方程与不等式等基础知识，同时也考查分类讨论、转化与化归、数形结合等思想方法.此类题综合性强，区分度高，是值得师生研究的题型.例7经过师生共同努力，给出了4种不同的解法，课后深入反思研究，又发现了第5种解法，具体过程如下：

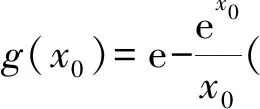
g(x0)max=g(1)=0，

即

g(x0)≤0.

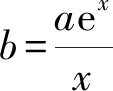
ae-b<0，

即

b>ae>0；

当a<0时，

ae-b>0，

即

0>ae>b.

故选项B正确.

解法5是将函数的零点或方程的根设为x0，将x0称为辅助元，再结合已知条件将其中一个参数用x0表示，也就是说用x0搭桥连接了条件与目标，使双参数函数问题转化为求单参数函数问题，难度系数明显降低.通过课后反思，教师不仅能得到宝贵的教学经验，还能将课堂实践提高到全新的高度，努力实现自我提升，从而提高试卷讲评课的效率.

总之，试卷讲评课是教学中的一个重要环节，想要提升高三数学试卷讲评课的有效性，教师必须在课前精心准备，在课堂中注重解题思维的渗透，课后及时反思总结，同时学生也要养成自我纠错、总结归纳、及时反思的好习惯，在师生共同努力之下，相信定会提高试卷讲评课的效率.