基于标准差偏离倍数的暂态事件检测算法

张广龙，任建文，周明

(华北电力大学，河北 保定 071003)

0 引 言

智能用电是智能电网发展的重要方向之一[1-2]，其中，负荷监测是实现智能电网的关键步骤之一[3-5]。目前的负荷监测系统可以分为两大类：侵入式负荷监测和非侵入式负荷监测。传统的侵入式负荷监测系统，会在每一个负载上都安装传感器，用以监测每个负载的运行情况。该方法硬件花费较高，系统的可靠性偏低，用户的覆盖范围也较小，因此侵入式负荷监测难以广泛应用[6]。非侵入式负荷监测(Non-Intrusive Load Monitoring, NILM)系统的特点是，只在电源的入口处安装了智能监测装置，这样就可以分析用户的整体内部用电负荷，并提供电气量信息诸如有功功率、无功功率、电能消耗、谐波等[7]。

非侵入式负荷监测可针对不同的行业，根据行业性质的不同可分为工、商、居民等几类，大部分研究集中在居民用户[8]。NILM通过入户端的智能测量装置，测量相关的电气量后，可以更方便地辨别处用户的负荷组成及状态等有用信息。

暂态事件检测是非侵入式负荷监测的重要研究部分，该过程将电力负荷的投切导致的采样序列某些统计特性上的一些突变信息提取出来并记录，为下一步的特征提取和负荷识别工作做预备工作。主流的暂态事件检测法分为似然比测试和序贯概率比检验。采用似然比测试方法的文献中，文献[9-11]提出通过滑动窗平均值来判断是否存在变点，提高了对噪声的抗干扰能力。采用序贯概率比检验法的文献中，文献[12]提出了基于滑动窗的双边累积和(Cumulative Sum, CUSUM)算法，这也是目前最常见的暂态事件检测法。文献[13]提出一种基于改进滑动窗的变点检测算法,能够准确判断负荷投切时间点，文献[14]通过变权重滑动窗来累积采样点与均值的偏差，文献[15]通过计算滑动窗内功率的标准差和电器投切前后稳态功率的差值,对投切事件进行检测。

已有的暂态事件检测算法需要已知投切负荷的有功功率跃变幅值，并依此设定功率跃变前后功率差的检测阈值，导致无法应用于多个有功功率跃变幅度不同的负荷同时投切的情况。为此，提出了一种基于标准差偏离倍数的暂态事件检测算法，该算法主要有两个创新性：

(1)相比起基于滑动窗的变点检测算法，不需要每检测一个负荷的投切变点就根据该负荷重新设置检测阈值，可以检测多个不同特性负荷投切的多个变点;

(2)相比起基于滑动窗的检测算法，检测速度和检测精度得到了大幅提升。

1 NILM系统的基本流程

NILM的硬件，是一个位置处于入户端的智能测量设备，测量节点的电气量信号。这些电气量信号包含不同的负荷信息，通过将这些电气量的特征提取出来，NILM系统中的负荷分解就可以被实现[6]。

NILM系统的基本流程中包括数据量测、数据处理、事件探测、特征提取、负荷识别。NILM的第1步是数据量测，可获得负荷的电气量信号。数据处理是NILM的第2步，包括噪声滤波、及电气量的处理等。对于处理过后的数据，进行事件探测，以得知用电设备的情况。对于探测到的事件，下一个步骤是特征提取，将事件前后的数据的特征提取出来，为负荷识别所用。负荷识别是NILM的最后一步，即将探测到的负荷与特征库中的负荷做比较，使用各种机器学习算法如k最近邻等进行分类，从而对负荷的种类进行识别。

针对事件探测部分进行研究工作,事件探测可归为变点检测问题，变点检测是指测算一个过程或序列所服从的统计模型改变时所对应的时间，该时刻前后将服从不同数学模型。本文选择采取变点检测作为事件探测的方法。

变点是指过程或序列的部分统计特性发生改变时所对应的时刻，在非侵入式负荷监测领域，指的是用电设备的运行状态变化或负荷投切过程中出现的暂态事件。

变点检测的数学描述如下：对一个给定的观测值数列y0,…,yn，判断假设H0与H1的真伪，其中，H0总是有：

y0,...,yn～Mθ0

(1)

H1:存在某时刻r，1≤r≤n，使得：

y0,...,yr-1～Mθ0

(2)

yr,...,yn～Mθ1

(3)

式中H0与H1表示假设0与假设1；M表示参数为向量θ的模型。式(1)表示该数列全部服从参数为向量θ0的模型，式(2)表示该数列在第r项之前服从参数为θ0的模型，式(3)表示在第r项之后服从参数为θ1的模型。若假设H1成立，还需估计出变点r以及模型参数θ0和θ1。

在事件探测中，主要估计的对象就是变点r的位置。在非侵入式负荷监测的变点检测中，估计的对象为有功功率数据的变点的位置。

2 标准差偏离倍数法的算法原理

负荷监测过程中采集到的有功功率数据P可以作如下分解：

P=μ+zσ

(4)

(5)

(6)

(7)

式(4)的实际意义为：任何一个测得的有功功率数据，都可以分解为该数据的平均值加上该数据的偏离倍数、标准差的乘积。

式(5)中n为从当前位置往前取的功率数据的个数;μ为前n个功率数据的平均值。式(6)中σ为前n个功率数据的标准差。式(7)中z为当前功率数据的标准差偏离倍数，i为功率数据的时间序号。

有功功率在各个不同偏离倍数下的分布规律如图1所示。

图1 有功功率在各个不同偏离倍数下的分布规律Fig.1 Distribution law of active power under different standard deviation multiple

图1中可知，偏离倍数的绝对值越大，其占据的比例就越低，出现的概率就越小。当有功功率在某位置的偏离倍数的绝对值过大，该情况在稳态情况下出现的概率过小，可由此判断该点已大概率处于变点状态，已不再处于稳态中。因此，偏离倍数是用于判断是否出现变点的重要依据。文中的偏离倍数法，就是以偏离倍数为判断变点的重要依据的。

3 标准差偏离倍数法的算法流程

提出的标准差偏离倍数法的流程图如图2所示。

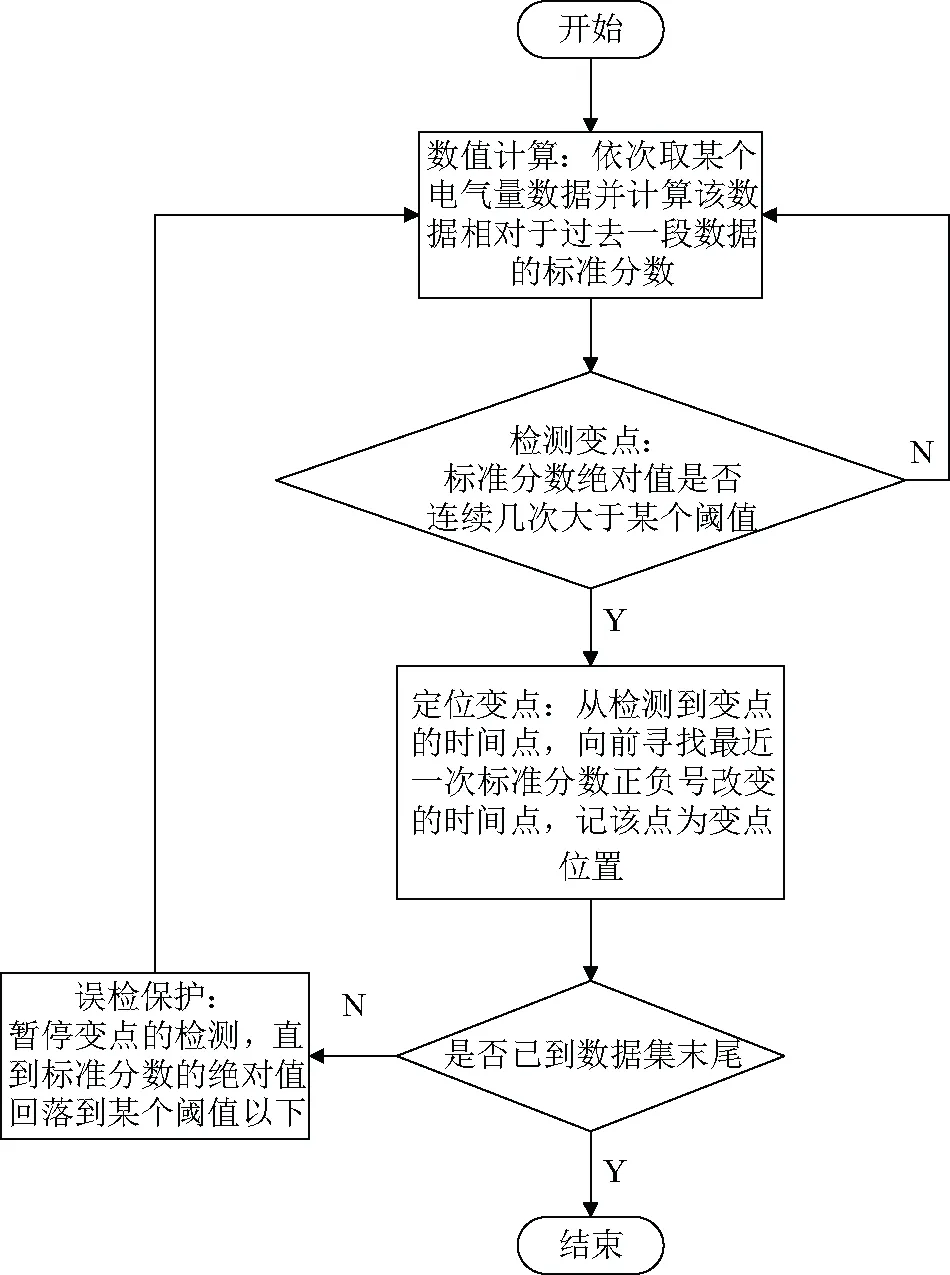
图2 标准差偏离倍数法流程图Fig.2 Flow chart of standard deviation multiple algorithm

3.1 数值计算

算法的第一步是数值计算。当我们正在对某个电气量数据进行实时检测，或者获取了一段电气量数据之后，这一段数据通常是总功率数据，当系统中有负荷投切时，电气量数据会产生变点，我们可以根据电气量数据的变点位置来确定负荷的投切时刻。该变点出现的真实时刻，文中定义为itrue。

按时间依次取每一个数据，并且根据所取的数据之前的一段数据，计算他相对于过去一段数据的偏离倍数。偏离倍数的定义如式(8)所示:

(8)

式中zscore(i,N)为第i个数据相对于过去N个数据的偏离倍数;Pi为第i个功率数据;PAVG(i,N)为第i个数据的前N个数据的平均功率;σ(i,N)为第i个数据的前N个数据的标准差。

3.2 检测变点

当偏离倍数的绝对值连续几次大于某个阈值时，便可确定变点已经出现了。当功率数据向上突变时，偏离倍数为一个较大的正数；当功率数据向下突变时，偏离倍数为一个较大的负数；当功率数据处于稳定状态时，偏离倍数大部分时间会在-2～2之间来回波动，反复穿越0点。之所以需要连续几次偏离倍数绝对值大于某个阈值，是因为功率数据处于稳定状态时可能会出现几个异常的噪点，该噪点可能会导致误检，而连续几次检测到特征再判断为变点已出现，可以提高检测算法的可靠性，减少误检情况。

若未能满足条件，则取下一个功率数据继续检测。将确定变点已经出现时的时刻，定义为ifound，那么从变点出现的真实时刻到确定变点已经出现时的时刻所经历的时间即为ifound-itrue，他代表在实时检测功率数据的变点时，从变点真实出现到检测到变点所消耗的反应时间。

3.3 定位变点

当检测到变点时，确定变点已经出现时数据所处的位置，和变点实际精确出现的位置有一段距离。由于功率数据在稳态状态时，偏离倍数在0附近波动且反复穿越0点，那么，当偏离倍数连续几次大于某个正数时，向前寻找最近一次偏离倍数由负数变为正数的位置，该位置即为最精确的出现向上突变的变点的位置；当偏离倍数连续几次小于某个负数时，向前寻找最近一次偏离倍数由正数变为负数的位置，该位置即为最精确的出现向下突变的变点的位置。

将精确定位变点位置的时刻，定义为istart，那么从变点出现的真实时刻到精确定位变点位置的时刻所经历的时间即为istart-itrue，其代表精确定位的变点时刻和变点出现的真实时刻之间的误差。

3.4 误检保护

在精确定位了变点的位置后，若此时已经接近数据集的末尾，则数据集已测试完毕，算法结束。若未接近末尾，则进行下一个变点的检测。

由于在变点过程中，偏离倍数容易在检测阈值附近出现波动，导致在同一个变点处出现多次误检，为了避免该情况，在检测到变点后，先暂停变点的检测，直到偏离倍数的绝对值回落到某个较小的阈值以下，再重新开始下一个变点的检测。

4 算例研究

本节通过算例的研究来验证所述偏离倍数变点检测算法的有效性，将分为3个算例。

算例1测量了大型电力工业用户的单个RL(Resistor Inductor)负荷正常启动情况下的检测用时和检测误差，并与当前最常用的变点检测算法—滑动窗双边CUSUM算法做对比。算例2验证了小型家庭用户的多个不同特性的负荷同时投切情况下的算法有效性。

4.1 算例1

本算例测量了大型电力工业用户单个RL负荷正常启动情况下的检测用时和检测误差，并与当前最常用的变点检测算法滑动窗双边CUSUM算法做对比。由于文献[12]是在使用IEEE 30节点仿真环境下进行的，在对比两种算法的检测用时和检测误差时，为了保证公平，本算例将在与文献[12]相同的测试环境下进行。IEEE 30节点系统如图3所示。

图3 IEEE30节点系统Fig.3 IEEE 30-bus test system

通过测量T1点的总功率来判断负荷的投切。测量额定电压为13.8 kV、额定功率为1 MV·A、功率因数为0.8的RL负荷启动过程中测量点的有功功率，采样频率为1 000 Hz。RL负荷启动前功率约为1 MW， RL负荷在i=420采样点处(0.42 s时)投入，测量点处的有功功率大约发生0.8MW的跃变。添加的白噪声标准差为2%。

在PSCAD/EMTDC中获得相关仿真数据，然后导入MATLAB中进行检验。仿真测试软件平台采用MATLAB R2017a，硬件平台使用CPU为AMD Ryzen 7 4800H with Radeon Graphics 2.90 GHz,内存为16 GB RAM的计算机。算例均采用该环境运行。

算法运行前需要进行一些运行参数的假设。参数有：计算偏离倍数时取的数据个数、偏离倍数绝对值的判断阈值及检测次数、重新开始变点检测的偏离倍数阈值。经过多次调整运行参数大小后可以得出：计算偏离倍数时所取的数据个数不宜过小，过小时计算出的功率均值受噪声影响较大，稳定性较弱；过大时计算出的功率均值变化反应过慢，不能准确地反应负荷投切改变后的稳态功率。结合采样频率和一般负荷的上升快慢，数据的个数取100以上为宜。偏离倍数绝对值的判断阈值一般采用“三倍标准差准则”，若过小(如小于2)会增加误检率，容易将小噪声误认为负荷投切；过大(如大于4)会增加漏检率，小功率负荷的投切过程中偏离倍数可能会无法达到阈值。检测次数若过小，则在稳态运行时容易将噪声误检为负荷投切，若过大则容易因满足条件的次数无法达到检测次数的要求而检测失败，因此一般取3次。重新开始变点检测的偏离倍数阈值只要远小于检测变点的偏离倍数判断阈值即可，一般小于2即可。

根据上述的对运行参数的分析，在该算例中，每个功率数据之前取100个数据进行偏离倍数的计算，偏离倍数的绝对值的判断阈值为3，检测次数为3次，检测到变点后先暂停检测，待偏离倍数的绝对值回落到1以下后再重新开始变点检测。

RL负荷启动过程中变点检测算法的参数变化如图4所示。

图4 RL负荷启动过程中变点检测算法的参数变化Fig.4 Parameter changes of change point detection algorithm during RL load starting

图4(a)的实线为有功功率的函数曲线；图4(b)的剧烈波动的实线为偏离倍数；只有高电平和低电平两个值的实线为alarm，为检测到变点的标志位。

在第420 ms，仿真系统的负荷投入，发生突变的确切时刻出现，记为itrue=420。在第426 ms时，检测到变点，alarm置为高电平，检测到变点的时刻记为ifound=426。此时往前推断距离本次alarm到高电平之前最近的一次偏离倍数改变正负号的时刻，为第420 ms，算法精确定位变点的时刻为istart=420，上述过程如图5所示。

图5 检测变点和精确定位变点的局部放大Fig.5 Local magnification for detecting change point and accurately locating change point

将检测用时定义为检测到变点的时刻与突变真实发生时刻的差值，本算例中检测用时为ifound-itrue=6 ms。将检测误差定义为精确定位变点的时刻与突变真实发生时刻的差值，本算例中检测误差=istart-itrue=0 ms。

将该仿真系统重复运行10 000次，测出10 000次的检测用时和检测误差的平均值，为5.673 2 ms和0.574 2 ms。在文献[11]中，当前最常用的变点检测算法滑动窗双边CUSUM检测法的检测用时和检测误差约为103 ms和5 ms。

考虑到算法的应用范围方面，偏离倍数法和滑动窗双边CUSUM法的综合对比如表1所示。

表1 两种非侵入式负荷监测算法的对比Tab.1 Comparison between two non-invasive load monitoring algorithms

从表1对比可知，偏离倍数法的各个方面都优于当前最常用的滑动窗双边CUSUM法，其优越的原因分析有以下几点：

(1)滑动窗双边CUSUM法是以不连续的、固定长度间隔取数据块的方式，而偏离倍数法是连续的计算每个数据的偏离倍数的方式，即时性更强，且偏离倍数相比起偏差累积和，对于偏差的敏感度更高，有突变就可以快速反应，这是偏离倍数法检测用时更少的原因;

(2)滑动窗双边CUSUM算法的精确定位变点位置的过程，是检测到变点后，将滑动窗退到检测到变点的位置后再次搜索定位，与检测变点的过程没有太大差别。而偏离倍数法在精确定位变点时，寻找距离检测到变点时最近的一次偏离倍数改变正负号的时刻，由于稳态状态下偏离倍数就在0附近上下波动，因此这种方法可以在精确定位变点时相对于检测变点有很高的提前量，误差极小;

(3)滑动窗双边CUSUM算法需要累积偏差和，必须提前已知投切前功率幅值和投切后的功率跃变幅值，并以此为基准设定检测的分辨率。偏离倍数法寻找偏离倍数绝对值过高的数据并将其检测为变点位置，投切后的功率跃变幅值仅会轻微影响算法性能指标(将在算例3着重分析)，无需提前已知投切前功率幅值和投切后功率跃变幅值;

(4)多个不同特性的负荷投切时，滑动窗双边CUSUM算法由于多个负荷的投切前功率幅值和投切后功率跃变幅值均不同，将无法使用。而偏离倍数法在多个不同特性的负荷同时投切时均可正常地检测出变点(将在算例2着重分析)。

4.2 算例2

本算例检验了小型家庭用户的多个不同特性的负荷同时投切下的算法有效性。实验数据来源于BLUED数据集[16]，该环境中家用电器负荷为单相负荷。 在该测试算例中，冰箱在第310 ms处启动，吹风机在第663 ms处启动，卧室灯在第929 ms处启动。将小型家庭用户的实测功率数据截取导入MATLAB中。该算例中的检测参数假设同算例1。测试结果如图6所示。

图6 多个不同特性的家用电器负荷启动过程中变点检测算法的参数变化Fig.6 Parameter changes of the change point detection algorithm during the start-up process of multiple household appliances with different characteristics

图6中的各曲线所代表的含义与算例1中相同。

在本算例中，冰箱启动这一暂态事件真实启动在第310 ms，在第324 ms被检测到，通过检查最近的一次偏离倍数改变正负号的位置，精确定位在第311 ms，因此检测用时为14 ms，检测误差为1 ms。吹风机启动这一暂态事件真实启动在第663 ms，在第678 ms处被检测到，精确定位在第664 ms，因此检测用时为15 ms，检测误差为1 ms。卧室灯启动这一暂态事件真实启动在第929 ms，在第942 ms处被检测到，精确定位在第930 ms，因此检测用时为13 ms，检测误差为1 ms。以上先检测到变点后精确定位的过程与算例1相同。

从BLUED数据集中提取到的家庭7种电器732组暂态功率负荷特征中随机选择500组进行偏离倍数法各项性能的测试，每一种电器都有500次测试结果，如表2所示。

表2 偏离倍数法检测不同家用电器时的检测用时、检测误差、误检率、漏检率Tab.2 Detection time, detection accuracy, false detection rate and missed detection rate of different household appliances detected by deviation multiple algorithm

由该算例可知，偏离倍数法在小型家庭用户的多个不同特性的负荷同时投切的情况下，具有很高的算法有效性，可见该算法并不局限于大型电力工业用户，可应对多种电气环境。

4.3 算例3

本算例测量了标准分数法在不同的噪声、有功功率阶跃幅度和RL负荷的时间常数下的检测用时、检测误差、误检率和漏检率，测试了算法面对恶劣干扰环境下的综合可靠性。为了便于控制各项变量的大小，本算例中的检测参数与仿真环境同算例1。

4.3.1 调整噪声大小

有功功率跃变幅度为0.8 MW，RL负荷的时间常数为20 ms，将白噪声的标准差逐渐增大，探究不同的噪声大小对检测用时、检测误差、误检率和漏检率的影响。测量结果如表3所示，每一次改变噪声大小检测10 000次，表3中的检测用时和检测误差均为平均值。

表3 不同的噪声大小对检测用时、检测误差、误检率、漏检率的影响Tab.3 Influence of different noise levels on detection time, detection accuracy, false detection rate and missed detection rate

由表3可知，随着噪声的增大，会对该算法的检测用时、检测误差和漏检率均带来不良影响，而对误检率毫无影响。

对于检测用时而言，由于噪声巨大，该算法测量得到的功率数据的标准差较大，有功功率的跃变带来的标准分数的爬升会更慢，因此噪声对检测用时的影响非常显著。

对于检测误差而言，由于精确定位变点的过程是发生在检测到变点的存在之后，寻找此前距离最近的一次标准分数改变正负号的位置，而在巨大噪声的影响下，有功功率的跃变使标准分数“改变正负号”的难度显然比“连续多次绝对值大于某个幅值”的难度小的多，因此噪声的增大对检测误差的影响要比对检测用时的影响小的多。

对于误检率而言，由于算法的误检仅出现在系统稳定运行时将噪声误认为是变点的情况中，而本算法是通过计算标准分数来判断变点的，在系统稳定运行时，标准分数的波动实际上与噪声的大小并无关联，因为噪声越大，当前功率数据与功率的均值的差值就越大，标准差也越大，而标准分数为当前功率数据与功率的均值的差值相对于标准差的倍数。因此，该算法在检测中并未出现误检，误检率基本不受噪声大小的影响。

对于漏检率而言，该算法的漏检主要出现在暂态事件状态下，标准分数没能达到“过去几次的平均数的绝对值大于某个幅值”的要求而检测失败。在噪声增大时，由于有功功率的跃变幅度不变，有功功率的跃变幅度相对于噪声会没有那么明显，会使得跃变时标准分数被显著削弱了绝对值，导致检测失败。而实际生产运行中并不会出现如此巨大的噪声，算法在系统正常运行的情况下是几乎不可能出现漏检的。

4.3.2 调整有功功率跃变幅度

白噪声的标准差为10%，RL负荷的时间常数为20 ms，将有功功率跃变的幅度逐渐增大，探究不同的有功功率跃变幅度对检测用时、检测误差、误检率和漏检率的影响。测量结果如表4所示，每一次改变有功功率跃变幅度检测10 000次，表中的检测用时和检测误差均为平均值。

表4 不同的有功功率跃变幅度对检测用时、检测误差、误检率、漏检率的影响Tab.4 Influence of different active power jump amplitude on detection time, detection accuracy, false detection rate and missing detection rate

由表4可知，随着跃变幅度的增大，会对该算法的检测用时、检测误差和漏检率均带来积极影响，而对误检率毫无影响。

事实上，有功功率的跃变相对于噪声越明显，也就是说有功功率的跃变幅度越大，噪声越小，标准分数在变点处的上升速度就越快，上升幅度也越大，算法的各项性能指标也就会越好。

仔细观察数据后可以发现，在RL负荷时间常数不变的情况下，检测用时、检测误差和漏检率指标与“有功功率跃变幅度/白噪声标准差”这一指标有显著的相关性，当“有功功率跃变幅度/白噪声标准差”越大时，有功功率的跃变相对于噪声就越显著，算法的各项性能指标也就越好。

4.3.3 调整RL负荷时间常数

白噪声标准差为2%，有功功率跃变幅度为0.8 MW，将RL负荷时间常数逐渐增大，探究不同的RL负荷时间常数大小对检测用时、检测误差、误检率和漏检率的影响。测量结果如表5所示，每一次改变时间常数大小检测10 000次，表中的检测用时和检测误差均为平均值。

表5 不同的时间常数对检测用时、检测误差、误检率、漏检率的影响Tab.5 Influence of different time constants on detection time, detection accuracy, false detection rate and missed detection rate

由表5可知，随着时间常数的增大，会对该算法的检测用时、检测误差均带来消极影响，而在测试中并未出现误检和漏检情况。

时间常数的增大与噪声的增大影响效果类似。时间常数增大后，功率数据的爬坡会更缓，会使得标准分数的上升速度显著放缓，因此对检测用时和检测误差影响较大。而由于“有功功率跃变幅度/白噪声标准差”这一指标并未改变，在变点处的标准分数上升幅度受影响较小，所以在测试中漏检率并未受到显著的影响。

4.3.4 算例结论

从算例3的整体测试结果来看，可以总结出以下结论：

(1)检测用时和检测误差主要和标准分数在变点处的上升速度有关，上升速度越慢，检测用时和误差性能越差。检测用时和检测误差的主要影响因素为RL负荷的时间常数，常数越大，功率曲线的上升速度越缓慢，标准分数的上升速度也越缓慢;

(2)误检主要出现在系统稳定运行时，本算例中暂未检测出有误检现象，噪声的增大并不会增加在稳定运行时的误检率;

(3)漏检主要出现在变点处未能满足变点检测的要求，标准分数绝对值未能连续一定的次数大于某个幅值，漏检率主要与标准分数在变点处上升能达到的最大幅度有关，因为标准分数能够在超过一定的幅值维持一定的次数才会判断为变点。漏检率的主要影响因素为“有功功率跃变幅度/白噪声标准差”，该因素会显著影响标准分数能上升到的最大幅度;

(4)总体而言，该算法能应对大部分的电气环境，有相当高的算法可靠性。

5 结束语

变点检测是NILM系统的重要组成部分，性能良好的变点检测算法可以为非侵入式负荷监测的特征提取和负荷识别环节打下良好的基础。

偏离倍数法是一种新型的暂态事件检测算法，不需要设定检测分辨率，可以应用于多种不同特性负荷同时投切的场景，抗噪能力强，检测速度快，精度更高，本文用实测数据验证了算法的有效性，为后续的特征提取、负荷辨识等工作打下了基础。