星型人字齿轮传动系统非线性分岔特性
白壮华, 林 何,2*
(1.西安工程大学 机电工程学院, 陕西 西安 710048;2.西安工程大学 西安市现代智能纺织装备重点实验室, 陕西 西安 710600)
齿轮装置广泛应用于大型重工机械和小型精密仪器等领域中,齿轮系统在各种非线性因素耦合干扰下,产生的振动和噪声极大地恶化了工作环境,因此为改善齿轮系统的工作稳定性及传动噪声,对齿轮系统动力学特性研究和优化是非常必要的[1-3]。星型人字齿轮传动系统因其功率密度高、传动比大和结构强度优等特点常应用于重载和可靠性要求高的设备中。为了解星型齿轮系统振动分岔行为,改善其响应性态,很多国内外学者对其动力学行为和振动特性进行了研究和优化[4-5]。Kahrarman[6]建立了单级行星齿轮传动系统的纯扭转动力学方程,通过数值求解得到了行星齿轮传动系统的模态和振型;邱星辉等[7]从研究现状、动力学优化设计和发展方向等方面对风力发电机行星齿轮传动系统动力学进行了综述;林何等[8]推导了行星人字齿轮啮合传动的时变啮合刚度动态梯形图,建立了人字齿行星齿轮传动的扭转非线性动力学模型,并对系统拟周期振动特性进行了分析;李同杰等[9]建立了直齿行星齿轮传动纯扭转动力学模型,分析了激励频率、齿侧间隙对该系统动力学特性的影响。Wei等[10]利用虚拟等效轴单元的动力学建模方法构建了人字齿行星齿轮系统的动力学模型;Mo等[11]基于集中参数理论和Lagrange方法建立了人字齿行星传动系统的动力学模型。
为研究啮合阻尼比对星型人字齿轮系统分岔特性的影响,课题组建立了星型人字齿轮系统纯扭转非线性动力学模型,利用Runge-Kutta法对动力学微分方程数值求解,通过不同转速下系统的相图、庞加莱(Poincaré)截面和分岔图对系统分岔演化过程进行研究,分析不同转速条件下啮合阻尼比对系统振动响应及分岔特性的影响。
1 系统非线性动力学模型
课题组采用集中质量法建立星型人字齿轮传动系统非线性动力学模型,系统端面动力学模型如图1所示。该系统功率主要由太阳轮输入并分流到行星轮,再由行星轮汇集到内齿圈进行输出。其中kspi,krpi(i=1,2,3)分别为太阳轮和行星轮、行星轮和内齿圈之间的啮合刚度,各弹性支承及啮合副均有阻尼和尺侧间隙。θs,θpi(i=1,2,3)和θr分别为太阳轮、第i个行星轮和内齿圈的旋转振动位移。

图1 星型人字齿轮系统传动系统端面模型Figure 1 End face model of star herringbone gear transmission system
为了更直观地表明各构件的运动情况,针对任一个行星轮i建立如图2所示的啮合型动力学模型。系统中所有齿轮均为人字齿轮,将每个人字齿轮视为由2个完全相同仅旋向相反的斜齿轮拼合而成,中间为欧拉梁单元连接,图中质量节点s1,s2分别代表太阳轮左、右2个斜齿轮;pi1,pi2分别代表行星轮i(i=1,2,3)左、右两侧斜齿轮;r1,r2代表内齿圈左、右2个斜齿轮;斜齿轮基圆螺旋角为β1,β2(左旋为正,右旋为负),故有β2=-β1;cspi,crpi(i=1,2,3)分别为太阳轮和行星轮、行星轮和内齿圈之间的啮合阻尼;espi,erpi(i=1,2,3)分别为太阳轮和行星轮、行星轮和内齿圈之间的综合传动误差;b为尺侧间隙;Ts,Tr分别为输入扭矩和输出扭矩。

图2 星形人字齿轮传动系统动力学模型Figure 2 Dynamic model of star herringbone gear transmission system
星型人字齿轮系统主要动力学参数如表1所示。行星轮个数为3,模数为4 mm,安装角αpi(i=1,2,3)分别为0,2π/3,4π/3,法面压力角αn为20°,基圆螺旋角β为22.5°,平均啮合刚度取2×109N·m-1,太阳轮输入功率为3 000 kW,刚度波动系数为0.1,输入、输出扭矩波动系数为0.5,尺侧间隙值为0.1 mm。
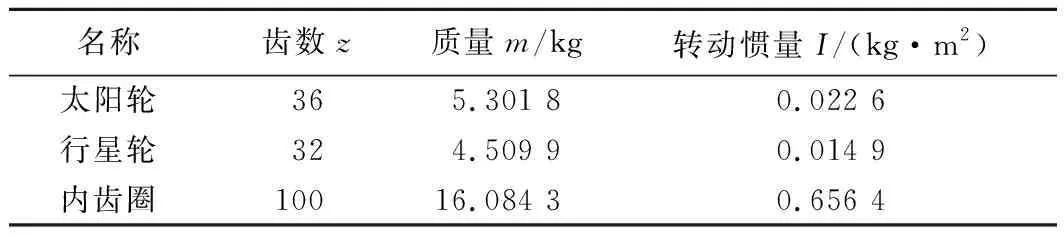
表1 星型人字齿轮系统部分动力学参数
根据牛顿第二运动定律构建系统动力学微分方程:
(1)
式中I为部件的转动惯量。
用傅里叶级数展开定义轮齿时变啮合刚度:
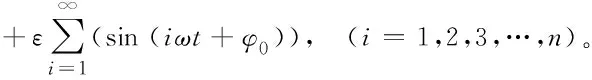
(2)
式中:К为时变啮合刚度均值,ω为啮合频率,ε为时变啮合刚度波动系数,φ0为啮合初始相位角。
定义初始相位角:
φspi=αt-αpi;φrpi=αt+αpi。
(3)
式中αt为齿轮端面压力角。
太阳轮和第i个行星轮左、右侧沿啮合线方向的相对位移Γspi1,Γspi2,内齿圈和第i个行星轮左、右侧沿啮合线方向的相对位移Γrpi1,Γrpi2,分别为:
(4)
式中:eij(t)=Esin (ωt+φ0),其中i=1,2,3,j=1,2,3,4;E为综合传动误差幅值。
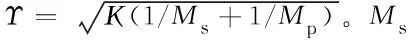
τ=Υt,Λ(τ)=Γ(t),δ=b/Δ。
系统消刚体位移和量纲为一的动力学微分方程:
(5)
(6)
(7)
(8)
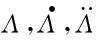
f(Λ)为量纲为一的含尺侧间隙碰撞位移分段函数,即:

(9)
2 系统分岔特性分析
阻尼比是齿轮系统中重要的动力学参数。为研究阻尼比对星型人字齿轮系统分岔特性的影响,取不同太阳轮转速下系统在阻尼比范围为0.05~0.20时振动位移Λsp11的分岔过程。
图3为太阳轮转速为7 000 r/min时系统的分岔过程。系统首先经历混沌状态,随着阻尼比的增大系统经历倒分岔从混沌进入倍周期,由倍周期进入二周期,最后进入稳定的单周期运动。图4和图5为系统在混沌状态和二周期状态下的相图和Poincaré截面图。
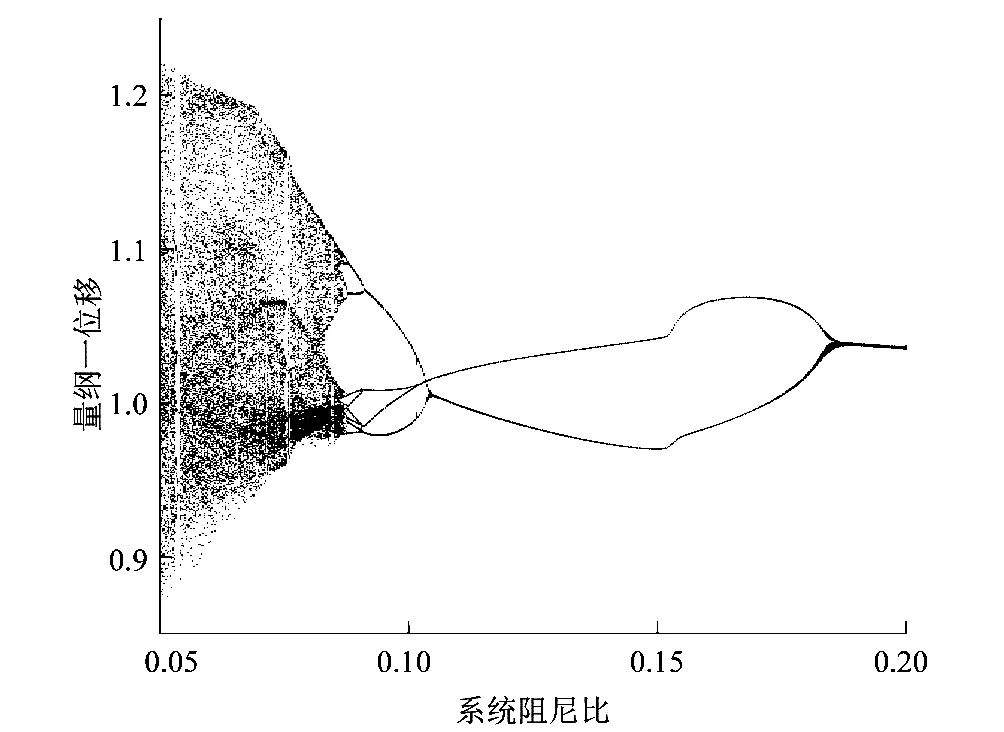
图3 转速为7 000 r/min时系统分岔过程Figure 3 Bifurcation process of system at 7 000 r/min
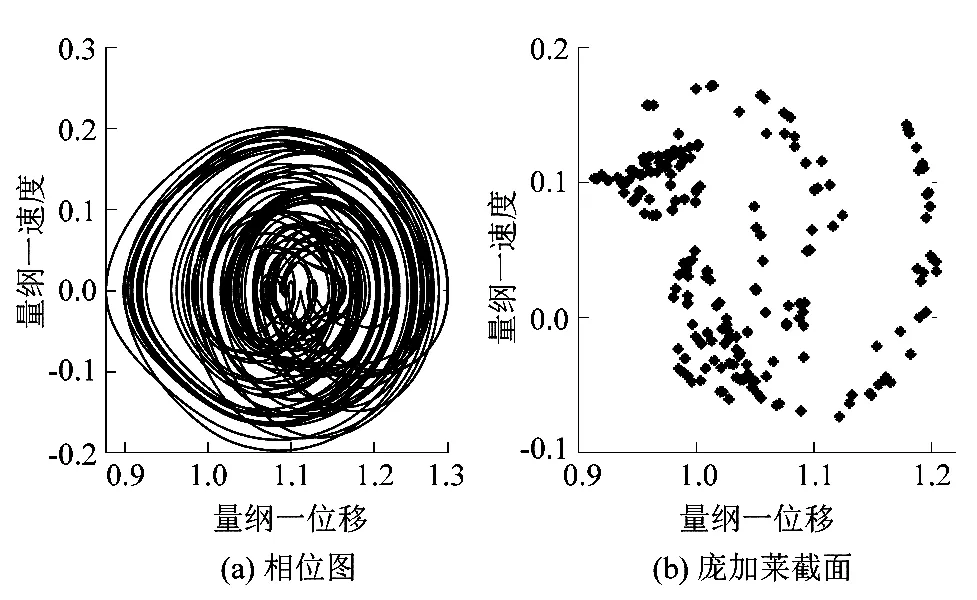
图4 阻尼比为0.06时系统混沌状态Figure 4 Chaotic state of system with damping ratio at 0.06
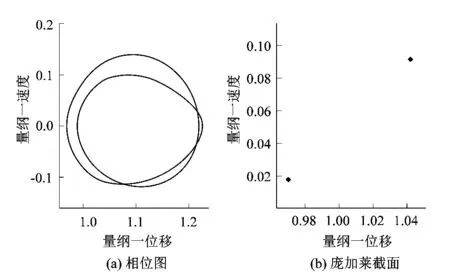
图5 阻尼比为0.15时系统二周期状态Figure 5 Two-cycle state of system with damping ratio at 0.15
图6为太阳轮转速为10 000 r/min时系统的分岔过程。系统首先经历混沌状态,随着阻尼比的增大系统直接跳跃激变为二周期运动,再由倒分岔进入单周期状态。图7和图8为系统在混沌状态和单周期状态下的相图和Poincaré截面图。

图6 转速为10 000 r/min时系统分岔过程Figure 6 Bifurcation process of system at 10 000 r/min
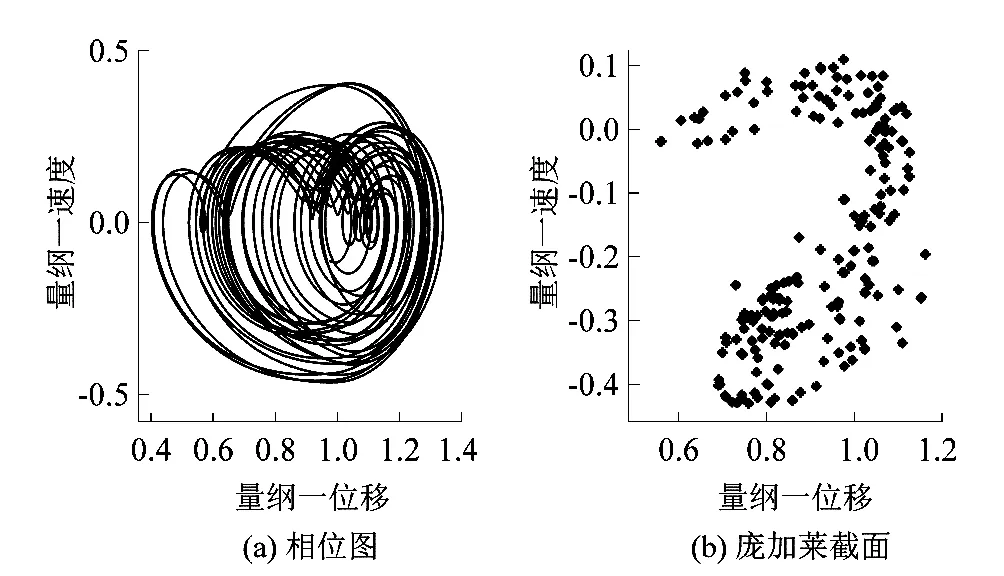
图7 阻尼比为0.06时系统混沌状态Figure 7 Chaotic state of system with damping ratio at 0.06

图8 阻尼比为0.18时系统单周期状态Figure 8 One-cycle state of system with damping ratio at 0.18
图9为太阳轮转速为13 000 r/min时系统的分岔过程。系统首先经历混沌状态,随着阻尼比的增大系统经历倒分岔从混沌进入四周期状态,再由四周期状态进入二周期状态,最后进入稳定的单周期运动状态。图10和图11为系统在混沌状态和四周期状态下的相图和Poincaré截面图。

图9 转速为13 000 r/min时系统分岔过程Figure 9 Bifurcation process of system at 13 000 r/min
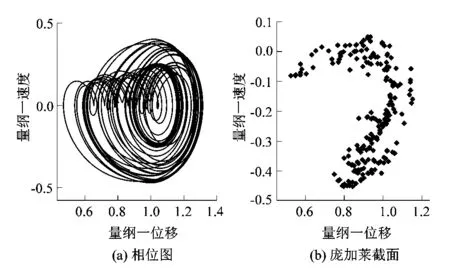
图10 阻尼比为0.06时系统混沌状态Figure 11 Chaotic state of system with damping ratio at 0.06
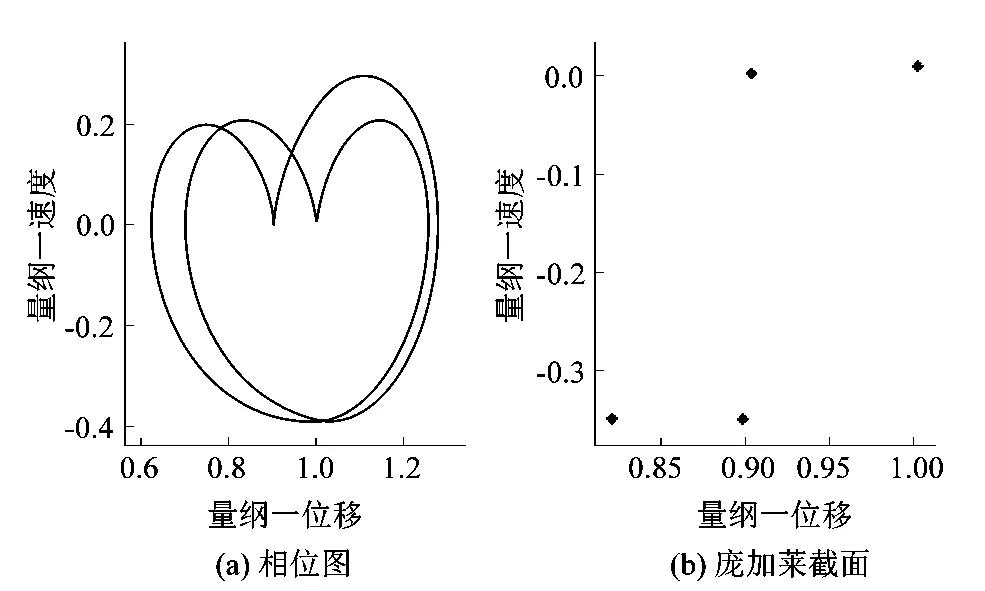
图11 阻尼比为0.10系统四周期状态Figure 11 Four-cycle state of system with damping ratio at 0.10
由不同转速条件下系统随啮合阻尼比的分岔过程及其在各种状态下的相位图和Poincaré截面图可以发现:在不同工况条件下系统随啮合阻尼比的增大,均由复杂的混沌状态逐渐演变为了稳定的单周期运动状态。因此星型人字齿轮系统在满足工况要求的前提下,适当增大齿轮系统啮合阻尼比可以有效避开混沌运动状态,减小振动响应,提高系统稳定性,起到减震降噪的功效。
3 结语
课题组构建了星型人字齿轮传动系统纯扭转动力学模型,对模型进行了消刚体位移和量纲一化,并利用Runge-Kutta法对其进行了求解;通过系统在不同转速条件下的分岔通道揭示了阻尼比对星型人字齿轮系统分岔特性的影响,并通过相位图和Poincaré截面图分析了系统在相空间状态下的动态轨迹行为。结果表明:在不同转速工况下星型人字齿轮系统动力学行为均随阻尼比的增大从最开始的混沌状态逐渐趋于稳定。因此适当增大系统啮合阻尼比可以有效规避混沌运动,起到减振降噪的作用。

