振动输送机橡胶弹簧优化设计
段 煜, 齐 瑞
(1.泛亚汽车技术中心有限公司, 上海 200100; 2.中铁十七局集团建筑工程有限公司, 山西 太原 030000)
当前,橡胶弹簧以多种形式应用于机械和电气/电子设备中,起隔离和减振的作用[1]。在实际使用过程中,橡胶弹簧存在参数稳定性差、疲劳寿命较短等问题,使得橡胶弹簧性能大打折扣,无法满足实际使用需求。因此,有必要通过优化设计去寻找最佳的橡胶弹簧结构参数。随着数值分析方法的普及,有限元法通常被用来预测橡胶弹簧的力学特性。Gong等[2]建立了包含温度谱和摩擦模型的橡胶非线性模型,并将其应用到高铁底盘悬挂的动力学分析中,研究了温度对于橡胶元件刚度的影响。Breg[3]提出了一种包含弹性力、黏性力和摩擦力的非线性橡胶弹簧动态模型,用于描述轨道车辆橡胶悬架部件力学行为,该模型用MATLAB和GENSYS实现,并将模拟结果与测量值进行了对比,结果显示有较好的一致性。孙蓓蓓等[4]基于悬架橡胶弹簧结构参数对轴向变形的灵敏度进行分析,以车辆的最佳非线性刚度曲线为优化目标,实现了对车辆悬架的橡胶弹簧结构参数的优化。杨善国等[5]提出了一种新型的振动筛橡胶弹簧数学模型,并用MATLAB对其进行了优化,优化后橡胶弹簧的体积有了明显减小。张亚新等[6]针对橡胶轴箱弹簧疲劳问题提出了一种基于等应力设计理念的优化方案,将该理念用于橡胶弹簧结构设计中,结果显示橡胶弹簧的疲劳寿命得到了增加。朱武等[7]基于有限元技术,将稳健性设计方法应用到橡胶弹簧静刚度曲线优化设计中,利用有限的实验次数,得到快速可靠的解决方案。荣继刚等[8]建立了橡胶弹簧参数化有限元模型,分析了结构参数对于橡胶弹簧横向偏移量的灵敏性,并对橡胶弹簧垂向刚度进行了优化。肖乾等[9]利用优化软件ISIGHT结合动力学软件UM对轨道列车的悬挂参数进行了优化,获得了最佳悬挂参数,优化之后的轨道车辆的平稳性得到了提高。传统的优化方法由工程师经验结合部分试验对橡胶弹簧进行改进,适用于结构较为简单的橡胶弹簧;随着对橡胶弹簧力学性能要求的提高,橡胶弹簧结构趋于复杂化,非线性有限元分析难度也在加大,传统方法就不再适用于橡胶弹簧的开发设计。因此,有必要对橡胶弹簧进行结构优化设计,以便能充分利用橡胶弹簧性能,满足各种设备的日常使用需求。
1 橡胶弹簧扭转刚度灵敏性分析
1.1 橡胶弹簧仿真模型
振动输送机主要是由振动槽体、机架、平衡体、驱动连杆、主振弹簧和支腿等部件组成。振动输送机的振动槽体和平衡体通过主振弹簧、驱动连杆铰支连接。电动机和驱动连杆安装在平衡体上,平衡体与支腿之间有隔振弹簧作用,隔离振槽和平衡体部分对地面的惯性力作用,确保振动输送机输送稳定性[10]64。振动输送机的结构如图1所示,驱动连杆作为振动输送机的关键部件,主要起着支撑、导向、主振弹簧的作用,对振动输送机的振动稳定性有重要影响,其结构形式如图2(a)所示。而橡胶弹簧作为驱动连杆的核心部件,其刚度特性是影响橡胶弹簧性能的重要因素,橡胶弹簧的结构组成如图2(b)所示。

1-振动槽体;2-驱动连杆;3-电机横梁;4-曲柄连杆机构;5-电机;6-支腿;7-机架;8-平衡体。图1 振动输送机结构示意图Figure 1 Structure schematic diagram of vibrating conveyor

图2 驱动连杆和橡胶弹簧的结构Figure 2 Structure of driven link and rubber spring
振动输送机作为一种低频大振幅的近共振机械,它是利用偏心轮的回转驱动平衡体,然后通过驱动连杆和橡胶弹簧激振振槽沿一定方向做线性往复运动,从而带动物料做定向抛掷运动,以达到输送物料的目的[10]64。振动槽体和平衡体通过驱动连杆铰接,运动方向相反,使振槽和平衡体朝相反方向振动。橡胶弹簧承受压缩、剪切载荷作用,在振动输送机的简谐运动中主要发挥着主振弹簧的作用。因此,橡胶弹簧刚度特性对于振动输送机的稳定运行有着重要意义。
利用非线性有限元分析软件ABAQUS建立橡胶弹簧动态有限元模型。由于在橡胶弹簧中4个橡胶棒作用形式相同,为了提升计算效率,笔者建立了1/4橡胶弹簧有限元模型如图3所示。构建了橡胶弹簧超弹性-黏弹性本构模型来表征橡胶弹簧黏弹特性,其超弹性材料参数取自其单轴压缩试验拟合的参数:C10=3.524 56,C01=1.523 46。其黏弹本构参数由三阶Prony级数来表示,具体参数取值如表1所示。由于橡胶棒变形远远大于外壳和内方管,所以将外壳和内方管设置为刚体,橡胶棒采用C3D8RH单元模拟,外壳和内方管采用R3D4单元模拟,橡胶弹簧整个有限元模型共有20 612个单元,22 455个节点。由于重点关注橡胶棒变形情况,所以橡胶棒有限元模型用较小的网格划分。橡胶棒与外壳和内方管之间设置面与面接触,切向接触采用库仑摩擦,参数设置为0.2,法向接触采用罚函数算法。为了分析方便,给外壳设置参考点Ⅰ,给内方管设置参考点Ⅱ,外壳与参考点Ⅰ,内方管与参考点Ⅱ之间设定刚体约束,外界激励载荷都是通过作用到参考点Ⅰ和Ⅱ来实现橡胶弹簧的扭转运动。根据橡胶弹簧动态试验工况设置相关边界条件,具体采用2个步骤:①静态分析,保持橡胶弹簧内部的方管不动,给外壳施加一定的径向位移,保持橡胶棒处于预紧和压缩状态;②稳态动力学分析,保证外壳不动,设置相应扫频范围对内方管施加振幅为1.5 mm的位移激励。

图3 1/4橡胶弹簧有限元模型Figure 3 1 / 4 finite element model of rubber spring

表1 三阶Prony级数
为了验证橡胶弹簧动态分析有限元模型的正确性,设计了橡胶弹簧动态扭转试验如图4所示。信号发生器可以控制输出的激励频率与振幅,功率放大器对信号发生器的信号进行增益,激振器通过与功率放大器连接输出不同的激励频率、振幅,由力传感器测得激振器激振力,通过LMS振动噪声测试设备进行数据采集,而激振器激振的橡胶弹簧的位移由单点激光测振仪进行测量。整个实验过程的测量的力-位移数据都被传输到LMS中,确保了数据采集的同时性。整个实验过程中保证了车间温度保持在常温,在采集数据之前首先进行了3次的预循环实验,以减小马林斯效应的影响。通过对橡胶弹簧加载不同激励频率,可以获得橡胶弹簧随激励频率变化的动态特性曲线。为了验证橡胶弹簧动态分析有限元模型的正确性,实验测试了橡胶弹簧在振幅为2.8和3.2 mm下动态特性,将实验采集的动态特性曲线与仿真曲线进行对比,结果如图5所示。从图中可以看出仿真结果与实验结果误差较小,验证了有限元模型的准确性,该模型可用于后续橡胶弹簧扭转刚度灵敏性研究。

图4 橡胶弹簧动态扭转实验Figure 4 Dynamic torsion test of rubber spring
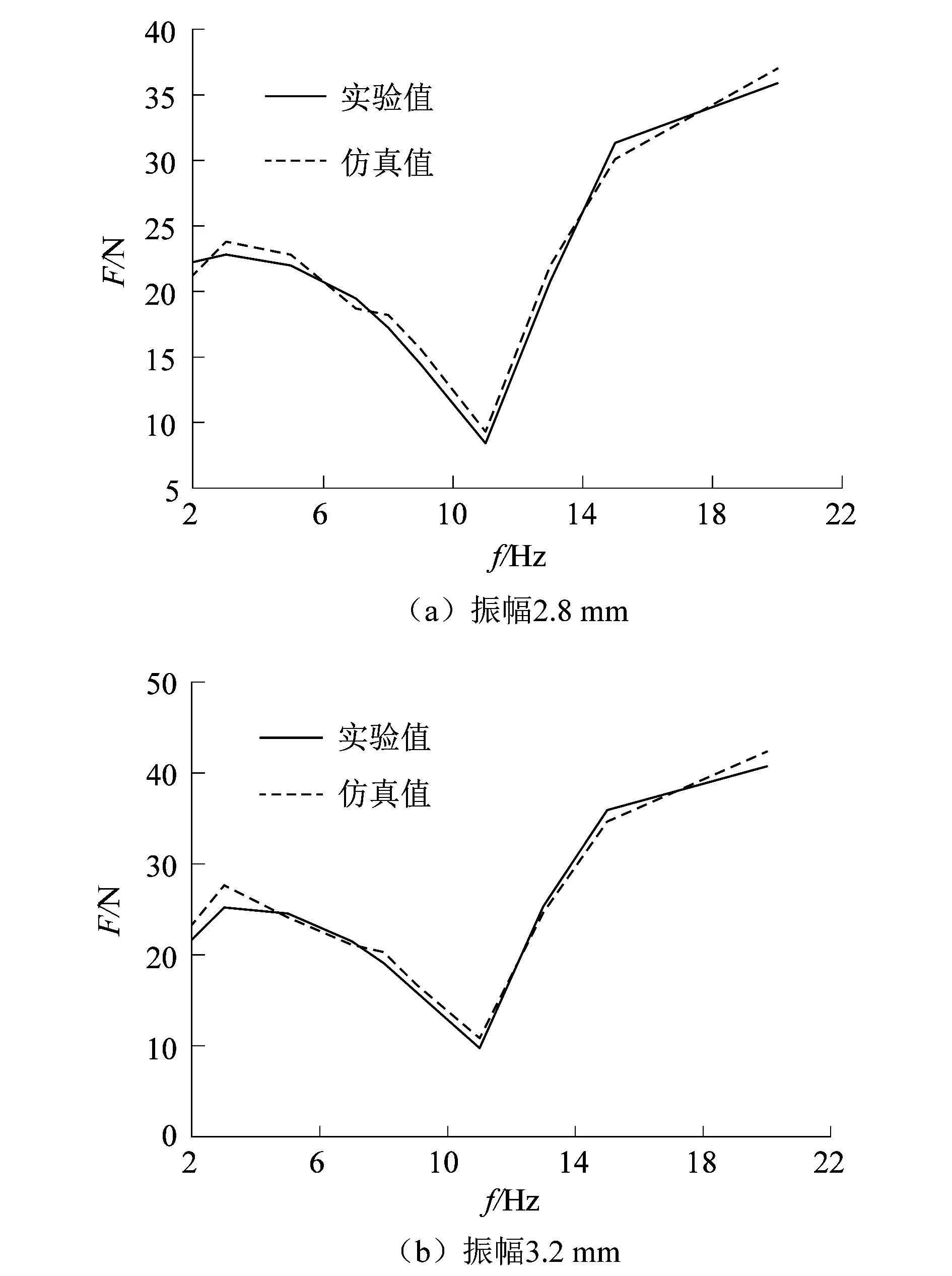
图5 不同振幅下橡胶弹簧扭转刚度的试验与仿真结果对比Figure 5 Comparison of test and simulation results of torsional stiffness of rubber spring under different amplitudes
1.2 灵敏性分析
橡胶弹簧作为振动输送机核心部件,其扭转刚度对振动输送机能耗有重要影响。而影响橡胶弹簧扭转刚度因素很多,如橡胶的结构参数(高度和直径)、材料参数(硬度)、预压量、激励频率、振幅和温度等,为了综合考虑多个因素对橡胶弹簧扭转刚度的影响,同时为了提高计算效率,基于橡胶弹簧动态分析有限元模型,探究了橡胶高度、直径、预压量、硬度、激励频率、扭转角度对橡胶弹簧扭转刚度的灵敏性。
响应面法是采用合理试验设计,获得一定的试验数据,通过多项式方程来拟合输入参数和响应值之间关系式,以此来代替物理模型完成相关的分析与优化工作。响应面法只需要通过拟合的多项式方程输入参数变量,就能得到输出的近似响应值,适用于解决非线性的多变量问题。
笔者选取响应面设计方法作为灵敏性分析的试验方法,选取了橡胶直径D、高度h、预压量P、激励频率f、硬度HD和扭转角度φ共6个因素,考虑到橡胶弹簧刚度、强度要求,笔者定义的各影响因素的取值范围如表2所示。

表2 影响因素的初始值和取值范围
考虑到选取的6个因素与响应值之间可能存在较强的非线性关系,笔者建立试验因素与响应值之间的二阶响应面模型,力求较为准确地描述试验因素与响应值之间的关系。利用拉丁超立方抽样得到200个样本点,构建这200个样本点与响应值扭转刚度之间的近似多项式模型。获得扭转刚度与橡胶弹簧各参数之间的关系如下:
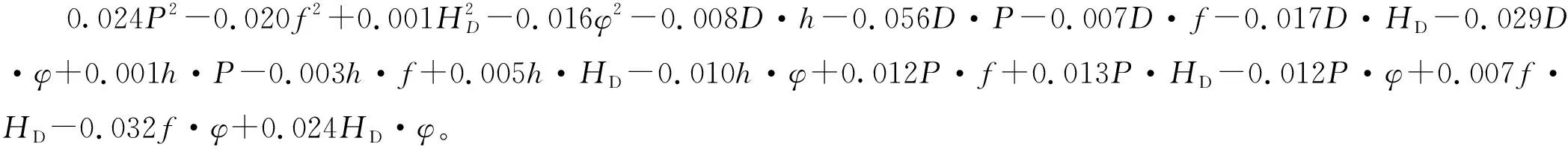
(1)
式中:X=[D,h,P,f,HD,φ],Kd(X1)为橡胶弹簧扭转刚度的估计值。
为了验证所生成的响应面模型的准确性,需要对其精度进行评估。笔者采用留一法来评估模型精度。对响应面模型的误差评估指标通常有相关系数R2和均方根误差RMSE。相关系数R2越接近于1,均方根误差RMSE越接近于0,表明所生成的响应面模型越准确。
(2)
(3)

响应面模型的相关系数R2=0.980 53,均方根误差RMSE=0.025 31,证明所建响应面模型精度较高,可以较为准确地描述试验因素与响应值之间的关系。
灵敏性分析是研究系统中参数变化对系统响应变化敏感程度的方法。一般是通过调节输入变量在范围内的值,观察输出响应值的变化情况,这样就可以得到各输入变量对于输出响应值的影响程度。通过灵敏性分析可以忽略对模型输出值影响较小的因素,确定对于模型输出响应有较大影响的因素,提高后续优化效率。在实际工程应用中,灵敏性分析中各优化变量为离散变量,单位不统一,为了能够量化各个因素对于输出响应值的影响程度,使得各个因素之间能够具有可比性,需要对灵敏性做一个统一化量纲处理[11]:
(4)
式中:Si(xi)为灵敏性,δKi为扭转刚度的相对误差,δxi为影响因素的相对误差,xi为影响因素,Δxi为影响因素在xi处的变化量,Ki为xi对应的扭转刚度,ΔKi为影响因素在xi处增量所引起的扭转刚度值。
在分析模型对于影响因素xi的灵敏性时,其余参数取标准值,保持不变,当Si(xi)的值越大,表明xi对于模型的影响程度越大。
依据上述灵敏性函数对于橡胶弹簧的6个影响因素进行灵敏性分析,影响因素的初始值可表示为如下矢量:
X=(x1,x2,x3,x4,x5,x6)=(19,60,15,7,70,7)。
(5)
在做灵敏性分析时,由于各影响因素单位各不相同且数量级相差较大,为了便于对各影响因素做对比分析,于是对于灵敏性曲线的横坐标进行如下定义:
(6)

将各参数代入式(4)进行计算,可以得到各影响因素对橡胶弹簧扭转刚度的灵敏性曲线如图6所示。

图6 影响因素灵敏性曲线Figure 6 Sensitivity curves of influencing factors
从图6中可以看出,橡胶弹簧的扭转刚度随着橡胶预压量的增加,灵敏性呈逐步上升趋势,但是上升趋势在逐渐变缓,最后趋于一定值;橡胶弹簧的扭转刚度随着橡胶硬度、扭转角度的增加,灵敏性呈逐步下降的趋势,表明橡胶硬度越大,扭转角度越大,其扭转刚度也就越小;橡胶弹簧扭转刚度对于激励频率的灵敏性呈现一种复杂的非线性关系,随着激励频率的增大,橡胶弹簧扭转刚度对其灵敏性先减小后增大,这与橡胶弹簧扭转刚度随激励频率变化规律是一致的,表明激励频率对其影响较大。而橡胶弹簧扭转刚度对橡胶硬度和直径的灵敏性几乎不变,表明橡胶直径和高度对橡胶弹簧扭转刚度的影响可以忽略不计。
为了更加直观地表示橡胶弹簧扭转刚度对各因素的灵敏性,引入影响百分比:
(7)
式中,λi表示了第i个因素对于模型响应值的影响百分比。
计算各因素对于橡胶弹簧扭转刚度的影响百分比,需取一基准值代入式(7),根据图6中拟合各因素Yi与灵敏度Si(xi)的多项式方程,将各因素的基准值代入式(7)计算;将各因素的基准值代入式(4)中可以得到橡胶弹簧扭转刚度对各因素的灵敏性Si(xi)。
在MATLAB中对图6中各个因素灵敏性曲线进行拟合,分别求得了S1(D),S2(h),S3(P),S4(f),S5(HD)和S6(φ)的函数关系式如下:
(8)
将各个因素的基准值代入式(8)中可得到基准值的Si(xi),然后将Si(xi)代入式(7)中,可以获得各个因素基准值对于橡胶弹簧扭转刚度的影响百分比,如表3所示。

表3 各影响因素对橡胶弹簧扭转刚度的影响百分比
由表3可以看出,橡胶弹簧扭转刚度对激励频率f(影响百分比为21.99%)、预压量P(影响百分比为16.78%)、硬度HD(影响百分比为35.35%)和扭转角度φ(影响百分比为20.94%)较为敏感,其中橡胶弹簧扭转刚度对橡胶硬度灵敏性最大;而对橡胶直径D(影响百分比为2.83%)和高度h(影响百分比为2.11%)灵敏性较差,表明这2个因素对橡胶弹簧扭转刚度的影响可以忽略不计,后续橡胶弹簧的优化设计将参考此次灵敏性分析结果。
2 橡胶弹簧优化设计数学模型
笔者对橡胶弹簧的结构、材料和预压量等参数进行优化,寻求影响振动输送机能耗的橡胶弹簧参数的最佳组合,以使橡胶弹簧在满足刚度和强度条件下振动输送机的能耗达到最低。基于上述各影响因素对于橡胶弹簧扭转刚度的灵敏性分析结果,忽略橡胶直径和高度对橡胶弹簧扭转刚度的影响,选取激励频率f、橡胶硬度HD、预压量P和扭转角度φ4个因素作为橡胶弹簧优化设计的设计变量。在振动输送机运行过程中,当橡胶弹簧扭转刚度处于最佳范围(亚共振)时,振动输送机能保持较好的性能和较低的能耗[12];同时考虑到橡胶弹簧在开发设计时各部件制造标准,对橡胶弹簧各部件的结构、材料等参数做一定约束。虽然目标函数为振动输送机的能耗,但是在优化分析时为了计算方便,以振动输送机的最小输出扭矩作为优化目标。
参考橡胶弹簧开发设计时各部件相关标准,结合橡胶弹簧实际工况,对橡胶弹簧4个优化变量的取值范围做了如表4所示的定义。

表4 优化变量初始值和取值范围
笔者所探究的是关于橡胶弹簧扭转刚度对于振动输送机能耗的影响,而目前的文献中没有找到关于橡胶弹簧扭转刚度对于振动输送机功率的计算公式。为了寻求橡胶弹簧扭转刚度与振动输送机功率之间的关系,笔者采用响应面方法拟合出2者之间的关系式。在拟合橡胶弹簧扭转刚度与振动输送机输出扭矩的多项式时,利用了图7所示振动输送机的ADAMS模型,该ADAMS模型已经通过加速度试验验证了模型的正确性。振动输送机输出扭矩M与橡胶弹簧扭转刚度Kd的关系如下:
(9)
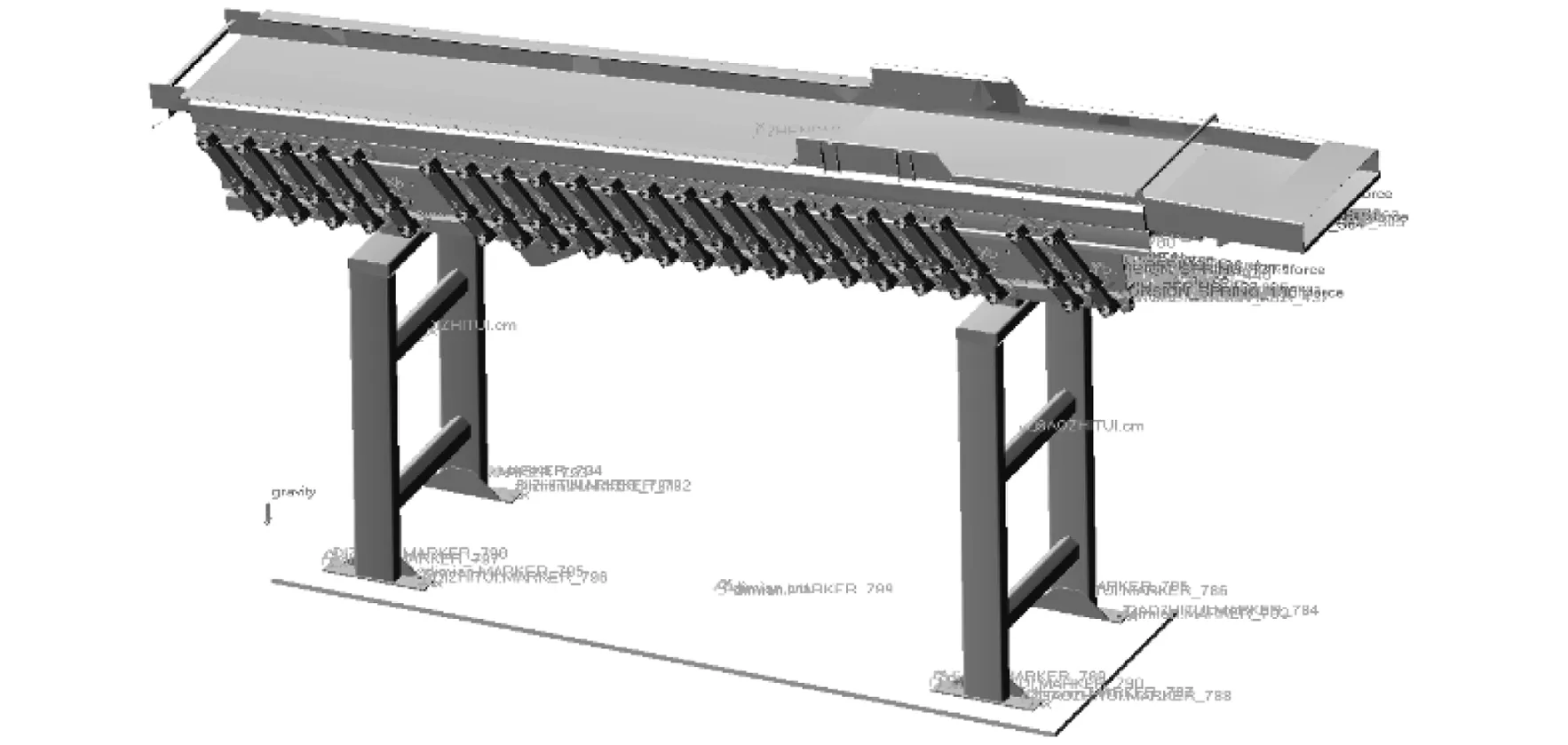
图7 振动输送机ADAMS模型Figure 7 ADAMS model of vibrating conveyor
以振动输送机橡胶弹簧的扭转刚度为约束条件,以振动输送机的输出扭矩作为优化目标,建立橡胶弹簧优化数学模型:

(10)
式中:M(Kd)为振动输送机输出扭矩的响应面函数,Kd(xi)为橡胶弹簧扭转刚度的响应面函数,xi=[f,φ,P,HD]。
式(10)是一个非线性优化问题,利用常规的数值方法求解较为困难,笔者采用遗传算法对橡胶弹簧的优化设计问题进行求解。
利用遗传算法对式(10)所建的数学模型进行优化计算,得到了橡胶弹簧在振动输送机最小输出扭矩下的最优参数。振动输送机最小输出扭矩优化迭代过程如图8所示。从图8中可以看出振动输送机的最小输出扭矩在迭代到20代之后收敛。优化之后的各参数结果如表5所示。从表中可以看出:优化后振动输送机的输出扭矩由110 456 N·mm减小到99 135 N·mm,振动输送机能耗减小了10.25%;且橡胶弹簧的激励频率更加靠近其固有频率(11.75 Hz),此时振动输送机只需输出一个较小的扭矩就可使橡胶弹簧产生较大位移,所以振动输送机的能耗得到了降低。
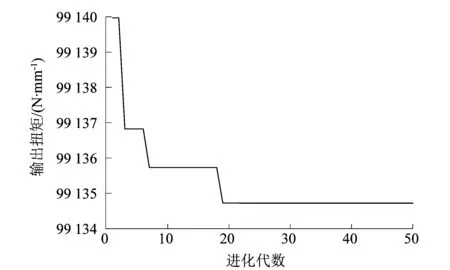
图8 振动输送机最小输出扭矩的迭代过程Figure 8 Iterative process of minimum output torque of vibrating conveyor

表5 优化后各参数结果
3 结论
笔者以振动输送机橡胶弹簧为研究对象,对橡胶弹簧的动态特性进行了实验与仿真分析,并基于分析结果对振动输送机的能耗进行了优化,获得了振动输送机最小能耗下橡胶弹簧各参数结果。得到的主要结论如下:
1) 在橡胶弹簧扭转刚度的灵敏性分析中,橡胶弹簧扭转刚度对激励频率f(影响百分比为35.35%)、预压量P(影响百分比为16.78%)、硬度HD(影响百分比为20.94%)、扭转角度φ(影响百分比为20.94%)较为敏感,而对橡胶直径D(影响百分比为2.83%)和高度h(影响百分比为2.11%)灵敏性差。
2) 在基于橡胶弹簧扭转刚度灵敏性分析结果对振动输送机能耗的优化中,采用遗传算法对振动输送机能耗进行优化,以振动输送机的输出扭矩来代表能耗高低,优化之前,振动输送机的输出扭矩为110 456 N·mm,优化后振动输送机输出转矩减小到了99 135 N·mm,能耗降低了10.25%。
笔者所采用的这一套振动输送机橡胶弹簧优化设计方法对实际工程中橡胶弹簧的开发设计具有一定参考意义,但是由于试验条件限制未对优化后振动输送机能耗进行验证,后续应对优化结果进行试验验证。

