基于语义生成与语义分割的机织物缺陷检测方法
马浩然, 张团善, 王 峰, 赵浩铭
(西安工程大学 机电工程学院, 陕西 西安 710048)
纺织业的重要性上至航空航天、生物医疗,下至服装家纺、包装材料。织物缺陷是影响织物可用性的关键因素,具有较多缺陷的织物将被判定为次品,影响销售甚至被销毁,同时织物缺陷率的上升也能反映出纺织机械故障的出现。所以织物缺陷检测是提升织物质量,监测纺机状态的重要步骤,快速、准确地检出缺陷对提升生产效率、提高产品质量都有重要意义[1]。
目前工厂中织物缺陷检测主要依靠人工进行,这不仅需要工人具有丰富的工作经验,且劳动强度大,对视力损伤严重。即使如此,人工也仅能达到70%的正确率,这意味着高质量的布匹不得不反复检测,这极大地提高了生产成本。
近年来,计算机技术快速发展,深度学习因其较高的检测正确率,已经逐渐成为织物缺陷检测的常用方法,使用较多的任务模式有分类、目标检测和语义分割[2-4]。分类任务仅能判别当前整张图像是否含有缺陷,并对缺陷分类,这种方式检测较为粗略,无法提供具体的缺陷位置;目标检测可以提取缺陷的中心位置和外接矩形的大小,能够更加精细地提供缺陷的信息,但无法提供缺陷的轮廓信息;语义分割可以提供织物缺陷的种类、位置、准确轮廓以及像素级精度的缺陷面积,对缺陷的描述较为全面[5]。因此语义分割任务在织物缺陷检测中的使用频率越来越高。
深度学习作为有监督学习,最为重要的是数据集的规模,数据集的规模越大、覆盖越广,越能反映出真实状态下的缺陷分布。一个全面的数据集对于获得一个泛用的、鲁棒的模型十分重要。在织物缺陷检测方面,现有的公共数据集数据量较少,且织物的种类也在日益增多,往往需要对拥有的有限的数据进行扩充[6]。传统的扩充方式采用翻转、旋转和缩放等方式,但这些方式只是对现有图像的处理,不能产生新的样本图像。
生成对抗网络(generative adversarial networks,GAN)[7]常常被用来扩充数据集,传统的GAN输入服从某种分布的噪声,输出生成的图像,这种方式可以产生新的图像,但这些图像仍需人手工标注,这增加了工作量。传统的GAN存在难以训练、模式崩溃等问题,作为数据扩充工具,传统 GAN在使用上存在困难。
近年来,语义生成作为GAN新的研究方向,广受关注,语义生成采用编码-解码器的方式,输入语义标签,输出与之对应的真实图像[8]。语义生成的提出使得语义分割的数据增强不再需要手工标注,仅需要随机产生语义标签,或对现有的语义标签进行数据增强,即可获得语义标签与对应的真实图像的一组数据,免去标注过程,可以在语义分割网络训练过程中实时增强。
传统GAN、深度卷积生成对抗网络(deep convolution generative adversarial networks,DCGAN)中[9],库尔贝特-莱布勒散度(Kullback-Leibler divergence),简称KL散度,和杰森-香农散度(Jensen-Shannon divergence),简称JS散度,在生成分布与真实分布不重叠时会造成梯度消失,导致网络无法收敛。瓦瑟斯坦生成对抗网络(Wasserstein generative adversarial networks,WGAN)[10]使用推土机距离(earth mover′s distance,EM距离)替代KL散度和JS散度,EM距离在2分布无重叠时也能良好地衡量真实分布与生成分布的距离。边界平衡生成对抗网络(boundary equilibrium generative adversarial networks,BEGAN)将判别器设置为编码-解码器的形式,通过重构误差的分布的逼近来代替真实分布的逼近,提升了训练速度,并且通过设置生成器与判别器损失的反馈机制来避免判别器过强导致的训练崩溃。
菲利普等[11]发现,在GAN的生成器训练中加入一些传统损失函数(L1损失函数)可以辅助训练,仅使用判别器的输出作为生成器的损失函数会导致生成的图像缺乏真实,仅使用L1损失函数会导致生成的图像十分模糊,2者融合可以更好地生成图像。
课题组采用BEGAN的网络结构[12],同时在生成器训练时添加加权的L1损失函数作为辅助,L1损失函数使用尺寸自适应加权函数进行加权,减少大尺寸缺陷模糊的问题。BEGAN同样采用EM距离评估生成分布和真实分布的差距,这可以避免KL散度和JS散度带来的梯度消失。课题组选用多样性比率γ(diversity ratio),用于控制生成网络在多样性和生成质量中的比例,同时比例控制原理(proportional control theory)的加入用于控制判别器对生成样本和真实样本重构误差期望维持在γ附近,从而避免判别器对生成样本过于严格而导致的训练崩溃。
1 语义生成
生成网络主要包括网络原理的构造和网络结构及参数的选择。生成对抗网络采用BEGAN的形式,生成器与判别器都采用编码-解码器的形式,判别器获取生成样本与真实样本的重构误差,损失函数采用EM距离,采用L1损失函数辅助生成器的训练。
1.1 原理及损失函数设计
传统GAN 的优化目标分为2部分:判别器D(xi)与生成器G(z)部分。
1) 判别器部分。
(1)
式中:xi为采样样本,Pr是真实图像分布,PG是生成器生成的图像分布。
对于判别器,在输入真实图像时,判别器D(xi)的期望输出越大越好,即Exi~PrlnD(xi)越大越好;在输入生成图像时,判别器D(xi)的期望输出越小越好,即Exi~PGln [1-D(xi)]越小越好。
2) 生成器部分。
Exi~PGln [1-D(xi)]。
(2)
对于生成器的优化目标,在对判别器输入为生成图像时,判别器的输出期望越大越好,即Exi~PGln [1-D(xi)]越小越好。
定义V(D,G)为优化目标,则有:

(3)
式中:PG=G(z),z~N(μ,σ2);V(D,G)为关于判别器与生成器的优化函数;∏(Pr,PG)是真实样Pr与生成样本PG的联合分布;z是符合某种分布的噪声,往往是正态分布。
在固定生成器G(z)时,最优的判别器
(4)
当判别器最优时,生成器的优化目标为:
(5)
引入KL散度和JS散度:
divKL(P1‖P2)=Exi~P1ln (P1/P2)。
(6)
(7)
式中P1与P2为不同的样本分布。
将生成器优化目标写成JS散度的形式:
2divJS(Pr‖PG)-2ln 2。
(8)
JS散度存在弊端,当真实样本分布Pr与生成样本分布PG分布完全不重叠时,JS散度恒为ln 2。即无论Pr与PG的分布多近或多远,JS散度为定值,这导致了梯度消失;而在实际情况中,Pr与PG的分布完全不重叠的情况十分常见,JS散度存在的弊端直接导致了原始的GAN难以训练。
EM距离W(Pr,PG)可以更好地衡量2个分布的差距。
(9)
对于联合分布样本σ,从中采样真实样本xr和生成样本xG,计算2者距离,取下界,定义为EM距离。
BEGAN将样本分布的优化转化为样本重构误差L的优化,即:
L(xi)=|xi-D(xi)|η。
(10)
式中η∈[1,2]。
除此之外,BEGAN还引入了多样性比例γ和比例控制原理,使得网络可以调节多样性和生成质量。
(11)

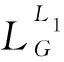
式中:Rd为标签中缺陷像素占比,yd为缺陷样本,yb为背景样本,μ为尺寸自适应权重,gd为生成缺陷样本,gb为生成背景样本,α为调节权重。
1.2 网络结构
生成器与判别器均采用编码-解码器的形式。编码器的网络结构如图1所示,输入经过纯卷积网络进行下采样,最终到15×15像素大小。传统的最大池化下采样不适用于语义生成任务,抑制低激活值不利于网络推导织物纹理。下采样部分采用卷积进行,卷积核4×4,步长为2。
解码器的作用主要是还原图像分辨率以及产生纹理。传统网络上采样为避免训练初期出现的周期性噪声而回避使用反卷积,转而采用双线性插值进行上采样。而在织物缺陷生成任务中,训练初期反卷积的周期性噪声的出现有利于织物底纹的推理,故采用反卷积进行上采样,同时串联一个3×3的卷积进一步产生纹理。解码器网络结构如图2所示。
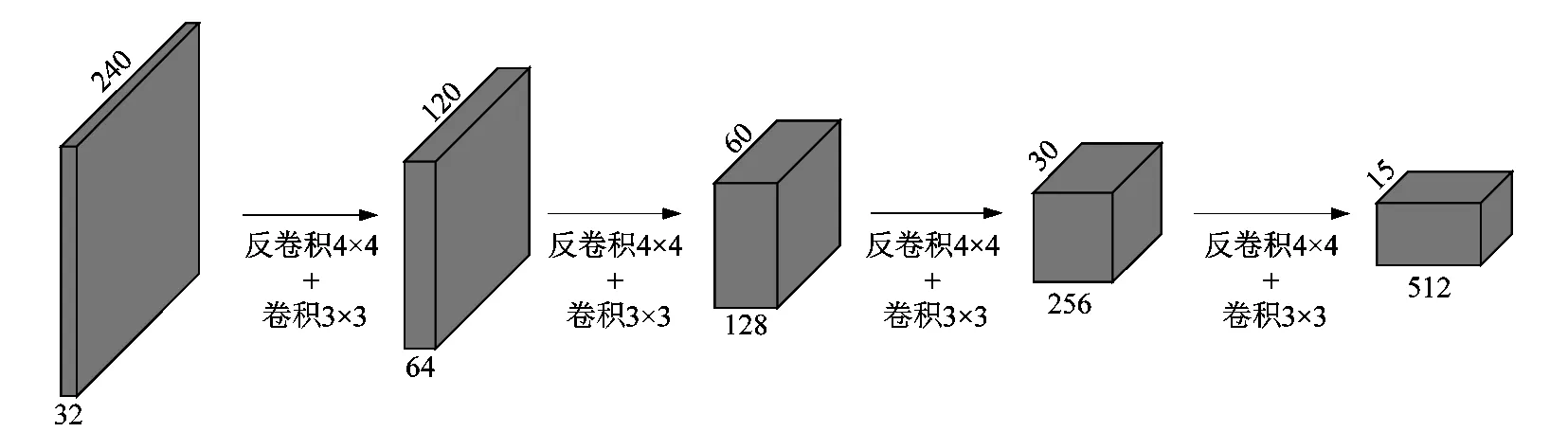
图1 编码器网络结构Figure 1 Encoder structure

图2 解码器网络结构Figure 2 Decoder structure
生成器与判别器采用相同的结构,唯一不同的是生成器的输入维度m=6,而判别器的输入维度m=3。模型添加了大跨度的特征融合,编码器的特征与其尺寸匹配的解码器特征相加。每个卷积层后添加BN层,使用ELU作为激活函数。整体采用大跨度的特征连接用于补充特征损失,辅助轮廓推导。图3所示为整体网络结构。
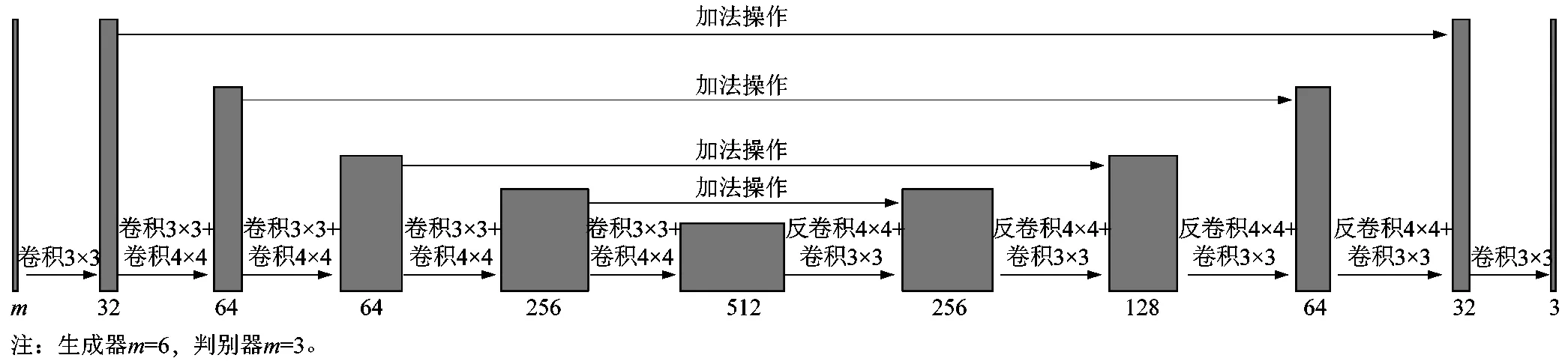
图3 生成器/判别器网络结构Figure 3 Generator/discriminator network structure
1.3 参数选择
在BEGAN的训练过程中,采用Adam优化器,β1=0.500,β2=0.999。为确保生成样本的多样性,在BEGAN的损失函数中,多样性比例γ=1,λk=0.001。在生成器训练过程中,图4中展示了不同α下的生成结果。在α=10.0时,生成图像清晰度低,真实性较差;在α=1.0时,清晰度提高;α=0.1时,生成图像清晰,真实性好。过高的L1损失函数权重α将导致生成网络多样性降低,且生成的图像较为模糊,故取α=0.1。

图4 不同α的生成结果Figure 4 Generation results for different α
2 语义分割
语义分割网络同样采用编码-解码器的形式,采用带空洞卷积的空间池化金字塔(atrous spatial pyramid pooling,ASPP)结构[13],最小下采样尺寸为30×30像素,这是保持织物缺陷不被缩放的最小下采样尺寸。设置尺寸自适应函数对Dice损失函数进行加权。
2.1 缺陷分析及损失函数设计
采样得到的织物图像分辨率为1 920×1 440像素,将整张图像作为网络输入将导致过高的显存占用,现有的深度学习框架在并行处理中能取得更高的处理效率,所以原图像被分割张数为4×3子图像,每张子图像经过双线性插值缩放到240×240像素。
织物疵点数据中,缺陷的分布并不均匀,有数量与大小的差距,语义分割中,每个像素点都被视为一个样本,那么织物缺陷的样本分布是十分不均匀的,呈现无缺陷样本与有缺陷样本的不均衡,缺陷的样本种类间不均衡。这种不均衡的现象导致像素数量占比较低的缺陷种类容易被忽略,这部分的损失容易被背景稀释,导致无法收敛或者滞后收敛。
Dice损失函数可以很好反映网络输出结果与目标的差距,这使得Dice损失函数在语义分割任务中被广泛地使用。原始Dice损失函数无法解决样本不均的问题,需要尺寸自适应函数解决样本不均衡的问题,将尺寸自适应函数改变相位如下:
式中:pd为网络预测输出,td为标签。
2.2 网络结构
语义分割网络同样采用编码-解码器的结构,如图5所示。残差块是编码器网络的基本组成,它可以更好地补充特征,同时还能防止网络退化。编码器将输入下采样至30×30像素的大小。240×240像素的图像中,缺陷的最小跨度为8个像素,故30×30像素的大小是保证缺陷不被缩放的最小下采样尺寸。在下采样后,采用了ASPP以不同空洞率Dr对解码器的底层特征进行采样,这是为了能够更好地提取到不同尺度的缺陷,同时也能扩大感受野,更好地检测尺度较大的缺陷。解码器中,使用了反卷积进行上采样,相较于双线性插值上采样,反卷积可以更好地推理轮廓,同时可以减少特征张量的维度,减少计算量。
2.3 参数选择
语义分割网络训练中,使用Adam优化器,Adam优化器参数β1=0.900,β2=0.999。训练采用使用余弦退火学习率,参数为T0=12,Tmult=2。
图5 语义分割网络结构Figure 5 Semantic segmentation network structure
3 实验结果
BEGAN在数据集上使用尺寸自适应L1损失函数与原始L1损失函数各训练了1 800次,使用测试集并进行数据扩充,增加缺陷多样性。语义分割网络在原始数据集上,使用原始Dice损失函数与尺寸自适应Dice损失函数各训练了1 000次。在使用BEGAN扩充的数据集上,使用尺寸自适应Dice损失函数训练1 000次。将结果进行对比分析。
3.1 BEGAN实验结果
图6所示为不同训练阶段下的缺陷图片生成图像,可以明显地观察到:使用尺寸自适应损失函数的生成结果优于原始L1损失,使用尺寸自适应L1损失函数的图像更加清晰,缺陷部分更加真实、清晰。

图6 原始L1损失函数与尺寸自适应L1损失函数生成图像对比Figure 6 Comparison of original L1 loss function and size-adaptive L1 loss function generated images
3.2 语义分割实验结果
图7所示为在原始Dice损失与尺寸自适应Dice损失下, 模型训练中验证集精度的对比。由图7可以看出在使用原始Dice损失时,模型的收敛出现了明显的滞后。这是因为在原始Dice损失下,小尺寸缺陷的损失被稀释,模型难以训练,负样本优先于正样本收敛,最终导致模型训练时间过长。尺寸自适应Dice损失函数能很好地解决这一问题,正、负样本损失分开计算可以减轻负样本对正样本的稀释。尺寸自适应函数对不同尺寸缺陷进行自适应权重分配,提高小尺寸缺陷的损失占比,由此解决正样本间不均衡问题。使用尺寸自适应Dice损失函数使得模型的检测精度提高了11.1%。

图7 Dice损失函数与尺寸自适应Dice损失函数模型准确率对比Figure 7 Accuracy comparison of Dice loss function and size-adaptive Dice loss function models
图8所示为使用BEGAN扩充数据集并且适应尺寸自适应Dice损失函数训练的模型的检测结果。模型可检测多种颜色及纹理的机织物,对缺陷的分割以及分类效果较好,能划分复杂形状缺陷轮廓,对于孔洞、断纱等小尺寸缺陷的检测效果优异。

图8 语义分割网络检测结果Figure 8 Semantic segmentation network detection results
图9所示为使用原始数据集训练出的语义分割网络与使用BEGAN扩充过的数据集训练的语义分割网络的性能对比。使用传统数据增强相较于使用原始数据集的提升较小,因为传统的数据增强只是对现有图片进行旋转、缩放、翻转等操作,本质上并未产生新的样本。使用BEGAN扩充的数据集更接近缺陷的真实分布,并且生成样本经过判别器筛选,扩充的缺陷图像皆是从随机语义标签重新生成的,缺陷图像更加多样,使得训练出的模型鲁棒性更好。
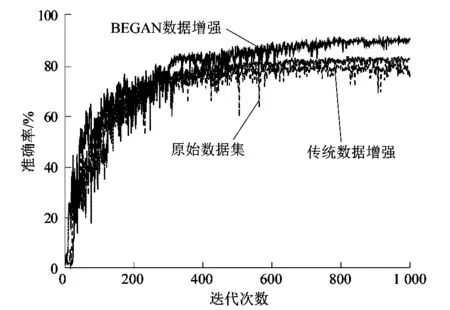
图9 不同数据增强方法对比Figure 9 Comparison of different data enhancement methods
均交并比(mean intersection over union,MIoU)为语义分割的标准度量,计算所有类别交集和并集之比的平均值:
式中:n为预测类别数量;TP表示模型预测为正例,实际也为正例,预测正确;FN表示模型预测为反例,实际为正例,预测错误;FP表示模型预测为正例,实际为反例,预测错误。
表1所示为不同数据增强方法下,模型的检测精度。使用BEGAN的语义生成方法获得了最好的效果,在测试集上获得90.8%的MIoU均值。

表1 数据增强方法对比
4 结语
课题组针对织物缺陷检测中的数据集缺失设计了语义生成网络,使用BEGAN平衡生成器与判别器,加入尺寸自适应的L1损失函数辅助训练,提升缺陷图像生成质量。语义生成的图像经过判别器筛选后进入扩充数据集,使得缺陷图像真实性更好。相较于传统数据增强方法,语义生成的图像更加真实,且能产出全新样本;相较于传统GAN进行的数据扩充,语义生成可以指定位置、形状和类别进行针对性生成,免去标注过程。
在语义分割方面,提出了尺寸自适应Dice损失函数,该损失函数能够解决样本不均衡问题,使得网络对小缺陷更加敏感, 提高检出率。尺寸自适应Dice损失函数相较于原始的Dice损失函数收敛更快,且最终得到的模型检测精度提高了11.1%。
使用BEGAN的免标注的数据集扩充,与传统数据增强方法进行对比,使用尺寸自适应Dice损失函数对模型进行训练,避免模型收敛滞后。最终在测试集上得到均交并比为90.8%,在GTX 1080Ti的运行速度可达到99帧/s。

