重载工况下行星齿轮传动啮合偏载分析

谭建军 李浩 杨书益 朱才朝 宋朝省 孙章栋

摘要：

為了深入研究重载行星齿轮传动多柔体变形下齿面载荷分布规律，提出一种计入结构柔性与齿轮副动态接触的行星齿轮传动耦合动力学建模方法。以某型兆瓦级风电齿轮箱行星轮系为研究对象，根据内齿圈、行星架结构及其边界特征，采用有限元缩聚理论建立内齿圈轮齿、行星架耦合点与弹性支撑之间的关联关系，利用齿轮副动态承载接触作为界面协调条件将各构件进行耦合，建立行星齿轮传动耦合动力学模型，分析了啮合偏载现象以及结构参数对啮合特性的影响。研究结果表明，作用在行星轮上的合弯矩以及行星架销轴非对称结构变形是造成啮合偏载的主要原因，系统共振会加剧啮合偏载程度；在共振区附近，齿轮动态啮合刚度与静态啮合刚度存在较大差异；增加销轴刚性、增大螺旋角可以改善啮合偏载程度，减小共振区系统振动，但在低转速区不利于系统减振，而增大行星架连接板刚性可以保持低转速区系统振动状态，同时减小共振区系统振动。

关键词：风电齿轮箱；行星轮系；结构柔性；内齿圈；动力学

中图分类号：TM614

DOI：10.3969/j.issn.1004-132X.2023.13.001

Study on Unbalanced Meshing Loads of Planetary Gear Transmission under Heavy-load Conditions

TAN Jianjun1 LI Hao1 YANG Shuyi1 ZHU Caichao1 SONG Chaosheng1 SUN Zhangdong2

1.State Key Laboratory of Mechanical Transmission，Chongqing University，Chongqing，400044

2.School of Mechanical Engineering，Hubei University of Automotive Technology，Shiyan，Hubei，442002

Abstract： To study the gear tooth load distribution affected by the multi-flexible body deformations of planetary gear transmission under heavy-load conditions， a coupled dynamics modeling method of planetary gear transmission that taken into account the structural flexibility and dynamic contact of gear pair was proposed. Taking a certain type of megawatt-class wind turbine gearbox planetary gear train as the research object， according to the ring gear， carrier， and their boundary characteristics， the finite element reduction theory was used to establish the correlations between the ring gear teeth， carriers coupling points and the corresponding elastic supports， and the dynamic load-contact of the gear pair was used as the interface coordination condition to couple these components， to establish the planetary gear transmission coupling dynamics model. The phenomenon of unbalanced meshing loads and the effects of structural parameters on the meshing characteristics were analyzed. The results show that the comprehensive bending moment acting on the planet gear and the asymmetric structural deformations of the carrier pin are the main causes of the unbalanced meshing loads， and the resonance of the system will aggravate this phenomenon. In the resonance region， the dynamic meshing stiffness differs greatly from the static meshing stiffness. Increasing the carrier pin stiffness and the helix angle may improve the meshing condition and reduce the system vibration in the resonance region. But in low-speed region， that is not good for system vibration absorption. Increase of the rigidity of the carriers connecting plate may keep the systems vibration state in the low-speed region， and reduce the system vibration in the resonance region.

Key words： wind turbine gearbox；planetary gear train；structural flexibility；ring gear；dynamics

收稿日期：2023-03-10

基金项目：

国家重点研发计划（2020YFB1506600）；国家自然科学基金（52105050）；广东省重点研发计划（2021B0101230002）；山西省重点研发计划（202102060301017）

0 引言

行星轮系具有结构紧凑、功率密度高以及传递扭矩大等优点，被广泛应用于风电齿轮箱中传递兆瓦级功率。风电齿轮箱是典型的重载（额定输入扭矩105～107 N·m）传动装置，近年来为了降低度电成本，风电机组逐渐朝10 MW+超大功率发展，这对风电齿轮箱承载能力、功率密度要求越来越高。为了满足更大功率传递需求，风电齿轮箱行星轮系各构件尺寸被设计得更大，在重载工况下容易产生过大的系统变形，造成齿轮啮合偏载，导致过大的系统振动、噪声以及动载荷，增大疲劳失效风险。因此，开展重载行星齿轮传动啮合偏载分析对指导风电齿轮箱优化设计具有重要意义。

行星轮系齿轮啮合过程本质上是一个复杂的多点啮合、多柔叠加的三维动态接触问题。其中，多点啮合主要体现在多个行星轮分别与太阳轮、内齿圈同时啮合，形成多对齿轮副同时啮合，并且在同一对齿轮副中，轮齿会周期性地啮入和啮出，形成多轮齿交替啮合状态。多柔叠加主要体现在太阳轮轴、行星架、内齿圈弹性变形、轴承支撑变形等多源变形量的非线性叠加，会改变齿轮接触状态。动态接触主要体现在各构件变形会改变啮合刚度、传递误差等内部激励，进一步反馈影响各构件变形，造成齿轮接触与系统振动之间存在显著的耦合作用。

国内外学者围绕行星轮系动力学开展了大量研究。ABOUSLEIMAN等［1］、ZHANG等［2］、许华超等［3］、张俊等［4］、刘向阳等［5］采用离散梁单元对内齿圈进行建模，分析了内齿圈模态和行星轮系动态响应。但此类建模方法无法考虑构件复杂结构特征，并且通常先计算得到齿轮啮合刚度，然后将其预置到行星轮系动力学模型中，并未考虑啮合刚度与构件动态位移的作用关系，齿面载荷计算精度有限，仍需进一步研究。

大量学者围绕齿轮副三维接触问题开展了深入研究。SAADA等［6］基于齿轮切片理论和集中参数法，建立了计入齿轮副准静态接触的行星轮系动力学模型，分析了系统刚度参数对齿轮共振频率的影响；随后，VELEX等［7-8］建立了计入齿轮副准静态接触的定轴轮系动力学模型，分析了齿轮错位量对齿面载荷分布的影响。

进一步细化模拟齿轮接触和考虑更全面的系统构件弹性变形与误差激励等，是提高仿真模型预测精度的关键。LIU等［9］基于齿轮切片理论与单位长度接触线啮合刚度均值，考虑齿面摩擦与齿廓误差激励，建立了人字齿定轴轮系动力学模型，分析了摩擦因数与齿廓误差对系统振动响应的影响。YOUNES等［10］考虑轴系柔性、齿廓误差，建立了计入齿轮准静态接触的定轴轮系动力学模型，开展了以降低传递误差与功率损失为目标的修形参数优化研究。ABOUSLEIMAN等［1］将内齿圈等效离散为若干梁单元，并结合切片理论和集中参数法，建立了计入齿轮准静态接触的行星轮系动力学模型，发现构件变形容易造成齿面偏载，而采用齿面修形可以有效降低系统振动［11］。AJMI等［12］通过引入Pasternak弹性基础假设，建立了切片齿轮弹性变形之间的关联关系，提高了定轴轮系斜齿轮准静态接触仿真精度，并发现了斜齿轮偏载现象。GUILBERT等［13］根据薄腹板齿轮结构特征，采用有限元子结构法与齿轮切片理论，建立了切片齿轮弹性变形之间的关联关系，构建了齿轮准静态接触模型，分析了薄腹板齿轮节径模态与系统动态响应。白恩军等［14］采用有限元法研究了轴系变形下齿面三维接触特性。袁冰等［15］建立了耦合转子系统多点啮合准静态接触分析模型，分析了轴系支撑布局形式对齿面载荷分布和系统动态响应的影响。

上述研究虽然为齿轮啮合三维接触分析提供了重要指导，但本质上属于准静态啮合过程，无法反映齿轮啮合过程中的动态接触现象。王涛等［16］、CAI等［17］、MATSUMURA等［18］以及CAO等［19］圍绕定轴轮系建立了计入动态位移影响的动态啮合刚度、齿面动态接触应力等计算模型，通过对比发现构件动态位移会影响齿面动态接触状态。为了建立构件动态位移与齿轮接触状态的耦合关系，PARKER等［20］采用有限元方法模拟了齿轮啮合动态接触过程。为了提高计算效率，ZHANG等［21］、赵百顺等［22］以及常乐浩等［23］将承载接触分析（loaded tooth contact analysis，LTCA）方法与有限元法或齿轮切片理论结合起来，通过预先提取影响齿面宏观变形的弯矩-剪切柔度系数矩阵，并结合赫兹接触方程动态计算齿面局部接触变形，建立了一种实用高效的LTCA数值计算方法。

目前，齿轮副准静态接触分析已被广泛应用于行星轮系动力学建模，而计入齿轮副三维动态接触和系统综合变形（如内齿圈、行星架等变形）的行星轮系动力学建模相关文献仍较少。实际上，由于风速的随机性，风电齿轮箱输入载荷波动频繁且数量级跨度大，容易造成复杂的构件变形，影响齿轮副啮合，改变内部激励，进一步反馈影响系统振动，因此对齿轮副啮合性能的要求较高。本文全面计入行星轮系各构件柔性，同时考虑行星轮系多对齿轮副在动态啮合过程中啮合激励与响应之间的关联关系，提出了行星轮系齿轮副动态承载接触分析（dynamic loaded tooth contact analysis，DLTCA）模型，并将齿轮副动态接触分析与行星轮系动力学求解相结合，建立了闭环的“啮合激励-系统振动-反馈影响”行星轮系动力学分析方法，分析了啮合偏载现象以及结构参数对啮合特性的影响。

1 NGW行星轮系构型

图1所示为被广泛应用于兆瓦级风电齿轮箱中的NGW行星轮系，主要包括行星架（c）、内齿圈（r）、太阳轮（s）和行星轮（p）。其中，行星架为双壁整体式结构，主要由连接板、侧板以及销轴等结构组成。输入扭矩（Tin）驱动行星架旋转，然后通过销轴带动行星轮转动（内齿圈固定），进而驱动太阳轮（负载Tout），最后通过太阳轮轴花键带动下一级构件转动。表1、表2分别为国内某型5 MW级海上风电齿轮箱行星轮系齿轮参数、轴承支撑刚度参数。其中，轴承支撑刚度参数通过Romax软件在额定工况下进行提取。内、外啮合副准静态啮合刚度见文献［24］。

2 行星轮系动力学建模

2.1 有限元缩聚模型

为了考虑具有非规则结构的行星架与内齿圈

几何特征，本文采用有限元子结构缩聚单元建立行星架与内齿圈模型。首先建立行星架与内齿圈有限元模型，然后根据行星架和内齿圈自身的边界约束条件设置主节点，并通过柔性多点约束［25］将主节点与对应的界面节点进行连接，最后采用固定界面模态综合法对行星架和内齿圈进行子结构缩聚，可得缩聚后行星架和内齿圈自由振动方程为

Mcq¨c+Ccq·c+Kcqc=0

Mrq¨r+Crq·r+Krqr=0（1）

式中，Mc、Mr分别为行星架与内齿圈质量矩阵；Kc、Kr分别为行星架与内齿圈刚度矩阵；Cc、Cr分别为行星架与内齿圈阻尼矩阵，采用Rayleigh阻尼计算［26］；qc、qr分别为行星架与内齿圈位移向量，包括主节点广义位移向量和内部保留阶数节点自由度。

图2和图3所示分别为内齿圈和行星架有限元缩聚模型。根据行星架与内齿圈结构特征，在其连接位置、轴承支撑和内齿圈轮齿处设置缩聚点，包括内齿圈轮齿和螺栓孔（图2）、行星架输入扭矩作用点、行星架轴承支撑点和销轴上-下风向行星轮轴承支撑点（图3）。

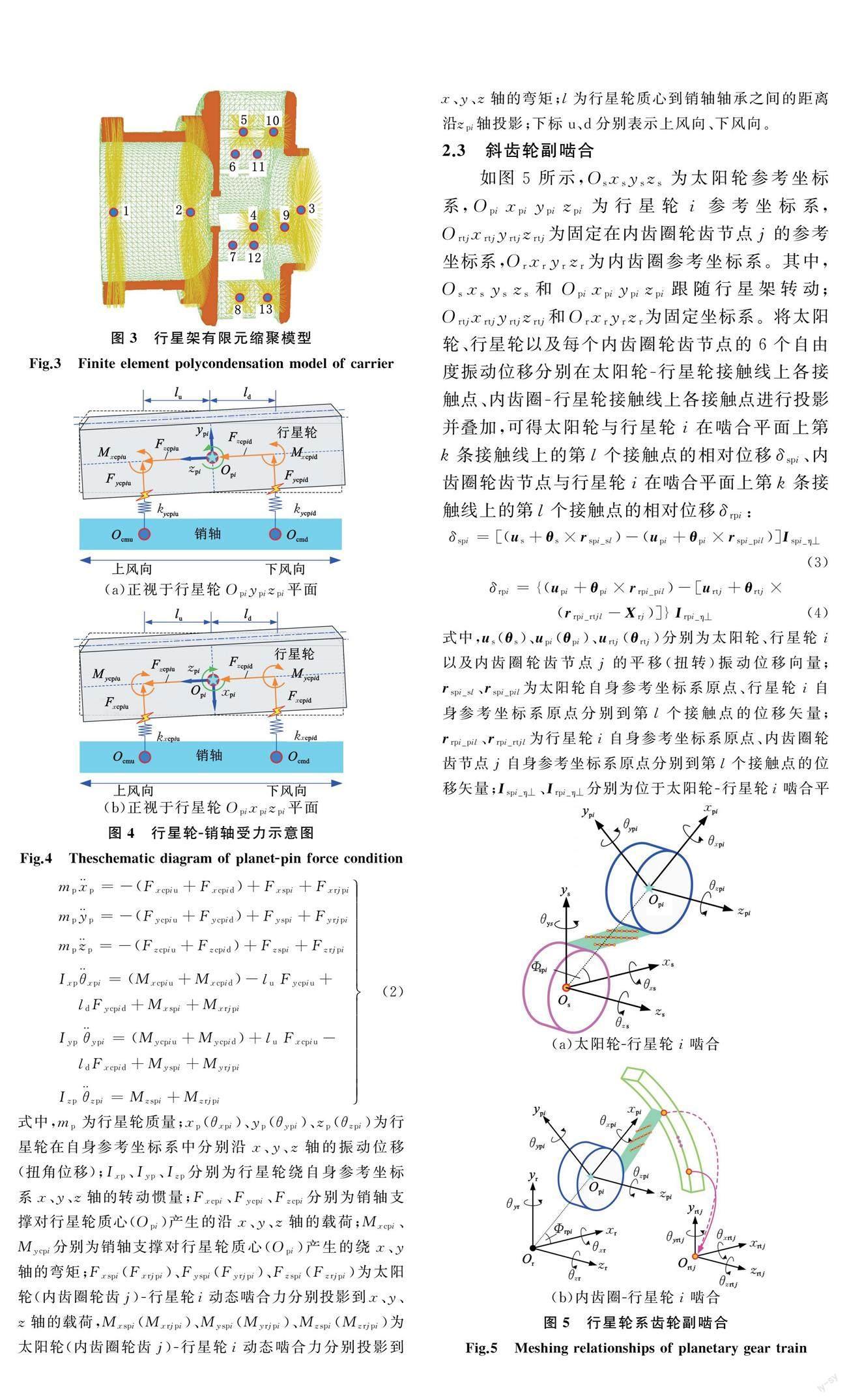
2.2 行星轮-销轴受力分析

为了保证行星轮轴承强度，常在行星架销轴的上、下风向位置处各安装一个同类型轴承，共同支撑行星轮，因此根据图4（图中Ocmu和Ocmd分别为销轴上、下风向轴承支撑节点位置）所示的行星轮受力情况，可建立行星轮受力平衡方程：

mpx¨p=-（Fxcpiu+Fxcpid）+Fxspi+Fxrjpi

mpy¨p=-（Fycpiu+Fycpid）+Fyspi+Fyrjpi

mpz¨p=-（Fzcpiu+Fzcpid）+Fzspi+FzrjpiIxpθ¨xpi=（Mxcpiu+Mxcpid）-luFycpiu+

ldFycpid+Mxspi+Mxrjpi

Iypθ¨ypi=（Mycpiu+Mycpid）+luFxcpiu-

ldFxcpid+Myspi+Myrjpi

Izpθ¨zpi=Mzspi+Mzrjpi（2）

式中，mp为行星轮质量；xp（θxpi）、yp（θypi）、zp（θzpi）为行星轮在自身参考坐标系中分别沿x、y、z轴的振动位移（扭角位移）；Ixp、Iyp、Izp分别为行星轮绕自身参考坐标系x、y、z轴的转动惯量；Fxcpi、Fycpi、Fzcpi分别为销轴支撑对行星轮质心（Opi）产生的沿x、y、z轴的载荷；Mxcpi、Mycpi分别为销轴支撑对行星轮质心（Opi）产生的绕x、y轴的弯矩；Fxspi（Fxrjpi）、Fyspi（Fyrjpi）、Fzspi（Fzrjpi）为太阳轮（内齿圈轮齿j）-行星轮i动态啮合力分别投影到x、y、z轴的载荷，Mxspi（Mxrjpi）、Myspi（Myrjpi）、Mzspi（Mzrjpi）为太阳轮（内齿圈轮齿j）-行星轮i动态啮合力分别投影到x、y、z轴的弯矩；l为行星轮质心到销轴轴承之间的距离沿zpi轴投影；下标u、d分别表示上风向、下风向。

2.3 斜齿轮副啮合

如图5所示，Osxsyszs为太阳轮参考坐标系，Opixpiypizpi为行星轮i参考坐标系，Ortjxrtjyrtjzrtj为固定在内齿圈轮齿节点j的参考坐标系，Orxryrzr为内齿圈参考坐标系。其中，Osxsyszs和Opixpiypizpi跟隨行星架转动；Ortjxrtjyrtjzrtj和Orxryrzr为固定坐标系。将太阳轮、行星轮以及每个内齿圈轮齿节点的6个自由度振动位移分别在太阳轮-行星轮接触线上各接触点、内齿圈-行星轮接

触线上各接触点进行投影并叠加，可得太阳轮与行星轮i在啮合平面上第k条接触线上的第l个接触点的相对位移δspi、内齿圈轮齿节点与行星轮i在啮合平面上第k条接触线上的第l个接触点的相对位移δrpi：

δspi=［（us+θs×rspi_sl）-（upi+θpi×rspi_pil）］Ispi_η⊥（3）

δrpi={（upi+θpi×rrpi_pil）-［urtj+θrtj×

（rrpi_rtjl-Xrj）］}Irpi_η⊥（4）

式中，us（θs）、upi（θpi）、urtj（θrtj）分别为太阳轮、行星轮i以及内齿圈轮齿节点j的平移（扭转）振动位移向量；rspi_sl、rspi_pil为太阳轮自身参考坐标系原点、行星轮i自身参考坐标系原点分别到第l个接触点的位移矢量；rrpi_pil、rrpi_rtjl为行星轮i自身参考坐标系原点、内齿圈轮齿节点j自身参考坐标系原点分别到第l个接触点的位移矢量；Ispi_η⊥、Irpi_η⊥分别为位于太阳轮-行星轮i啮合平面上且垂直于接触线方向的方向矢量、

位于内齿圈-行星轮i啮合平面且垂直于接触线方向的方向矢量；Xrj为内齿圈轮齿节点j在全局坐标系中的位置坐标。

将式（3）和式（4）反向投影至自身参考坐标系中，可得δspi、δrpi对应的啮合向量［1］：

V（l）spi=Vs|6×1

Vpi|6×1（5）

V（j）rpi=Vpi|6×1

V（j）r|6×1（6）

式中，Vs、Vpi、V（j）r分别为太阳轮、行星轮i、内齿圈轮齿节点j在自身参考坐标系的广义位移向量。

2.4 行星轮系动力学模型

根据太阳轮轴、内齿圈、行星架和行星轮节点自由度及其耦合关系，定义系统节点在自身参考坐标下的广义位移向量为

Xsys=（XTc，XTr，XTp1，…，XTpNp，XTs，qcq，qrq）T（7）

式中，Xc、Xr、Xs、Xp分别为行星架、内齿圈、太阳轮轴以及行星轮的广义位移向量；Np为行星轮数量；qcq、qrq分别为行星架和内齿圈保留的内部节点模态坐标。

其中，太阳轮轴采用Euler-Bernoulli梁单元建

模［27］。内齿圈螺栓孔等效支撑刚度本文取值1×

109 N/m（N·m/rad），太阳轮轴等效支撑刚度本文取值1×108 N/m（N·m/rad）。

如图6所示，根据式（7）中各节点编号，将各构件质量矩阵、刚度矩阵以及阻尼矩阵进行组装，可建立行星轮系动力学模型：

MsysX¨sys+CsysX·sys+KsysXsys=Fsys（8）

式中，Msys、Ksys和Csys分别为系统质量矩阵、刚度矩阵与阻尼矩阵；Fsys为系统激振力矩阵，包括输入扭矩与负载。

3 斜齿轮副动态承载接触模型

基于传统静态承载接触模型建立斜齿轮副动态承载接触模型，如图7所示。当已知齿轮副动态传递误差与静态传递误差且忽略齿面摩擦时，可得第k对啮合齿面上各接触点变形协调条件为

C（k）bfFk+uck-Yk=δk-εk（9）

式中，C（k）bf为各接触点的柔度系数矩阵，主要由齿轮弯曲-剪切变形和轮体变形组成；Fk为作用在各接触点上的载荷；uck为各接触点的接触变形列向量；Yk为各接触点接触后的剩余间隙列向量；δk为各接触点对应的动态传递误差；εk为各接触点的初始间隙列向量，包含齿轮制造误差、修形以及齿侧间隙等。

本文选用切片法理论计算C（k）bf［28］和uck［29］，其表达式分别为

C（k）bf=λkp11+λkg11…λkp1l+λkg1l…λkp1n+λkg1nλkpl1+λkgl1…λkpll+λkgll…λkpln+λkglnλkpn1+λkgn1…λkpnl+λkgnl…λkpnn+λkgnn（10）

uck=［u（k）c1，…，u（k）cl，…，u（k）cn］T

u（k）cl=FlπbE*（ln（πb3E*（ρp+ρg）2Flρpρg）+1）（11）

式中，λkpln、λkgln分别为主、从动轮对应的接触点l对接触点n的弯曲-剪切柔度；u（k）cl为接触点l对应的接触变形；Fl为作用在接触点l的载荷；E*为等效弹性模量；ρ为接触点l对应的等效曲率半径；b为接触点i对应的齿宽。

第k对啮合齿面上各接触点需要满足如下载荷判断条件：

Yl=0，δl>εl，if Fl>0Yl>0，δl≤εl，if Fl=0（12）

式中，Yl为接触点l在接触后的剩余间隙；δl为接触点l的动态传递误差；εl为接触点l的初始间隙。

當求解接触方程得到Fk后，根据式（9）定义，可以根据啮合线各接触点弹性变形计算得到单对轮齿动态啮合刚度km：

km=∑nl=1kl=∑nl=1Flδl-εl（13）

式中，kl为接触点l的动态刚度，kl=k（l）bf+kcl，k（l）bf、kcl分别为接触点l的弯曲-剪切刚度、赫兹接触刚度，可以分别通过式（10）、式（11）得到的柔度系数矩阵和接触变形进行计算。本文暂不考虑齿轮修形与齿形误差，令εl=0。

4 齿轮副动态接触与系统动力学耦合方法

齿轮副动态啮合过程是一个“啮合激励-系统振动-反馈影响”的闭环耦合过程。通过求解预先给定位移与速度初值的系统动力学方程，根据齿轮副动态承载接触方程（式（9）～式（12））可得影响系统振动的啮合激励（接触点动态载荷）；将啮合激励重新代入系统动力学方程（式（8））并求解，可得系统振动响应；再通过式（3）～式（6）得到齿轮副动态承载接触方程（式（9）～式（12））的反馈影响，最终建立上述闭环耦合分析流程。

本文提出了基于精细积分法（PIM）［30］的齿轮副动态接触与系统耦合振动求解方法，具体流程如图8所示。V、X分别为不同时间步下啮合向量（式（5）和式（6））和对应的构件振动位移向量（式（7））。其基本思路是当给定载荷参数、几何参数与仿真参数后，首先基于预先给定的位移和速度向量初值，可得各构件振动位移作用在各接触点上形成的相对位移δdt+Δt（k），同时根据行星轮转角θzpi，dt+Δt（k）可得齿轮副弯曲-剪切柔度系数矩阵（C（k）bf）dt+Δt（k）；然后求解式（8），可迭代得到作用在各接触点上的载荷F（f）dt+Δt（k），生成受振动位移影响的齿轮副动态啮合激励（“系统振动-啮合激励”）；最后根据更新后的各接触点载荷与当前时刻各构件振动位移和速度，利用PIM求解下一时刻系统响应，实现将齿轮副动态啮合激励再反馈作用于各构件振动位移（“反馈影响”），并不断地重复上述迭代过程。在计算时，PIM仿真步长取5×10-5 s，各接触点载荷收敛容差ζ=1×10-3。

5 结果讨论与分析

5.1 有限元验证

由于整体的行星轮系有限元模型计算规模大、效率低且收敛困难，因此为了验证本文模型，建立了局部的太阳轮-行星轮-内齿圈啮合有限元模型，如图9所示。在此模型中，将驱动转角（θzc=0.2 rad）施加在仅传递旋转运动的刚性行星架上，负载（Tout=2.048×105 N·m）施加在太阳轮上，同时在齿圈螺栓孔处设置线性弹簧-阻尼边界约束，本文取k=1×109 N/m（N·m/rad）。其中，将行星架视作刚体主要是由于行星架变形主要影响齿面载荷分布，但对齿面载荷的合力影响较小，同时兼顾计算效率与收敛性。将有限元模型得到的轮齿接触力与本文模型进行对比，如图10所示。

相比于局部的太阳轮-行星轮-内齿圈啮合有限元模型，本文模型全面考虑了行星架、内齿圈与太阳轮轴柔性，因此两者计算得到的轮齿接触力略有差异，但本文模型得到的轮齿接触力整体变化趋势和峰值位置与有限元模型结果一致，验证了本文模型的正确性。此外，本文模型计算效率明显高于有限元模型，当刚体行星架旋转0.2 rad时，有限元模型计算时间超过8 h，而本文模型仅需要约20 min（计算机配置为CPU AMD 3700X，RAM 32.0 GB）。

5.2 斜齿轮啮合偏载分析

图11所示为不同工况下太阳轮-行星轮、内齿圈-行星轮啮合齿面载荷分布情况。从图中可知，随着输入扭矩增加，齿面载荷等比例增大；太阳轮-行星轮、内齿圈-行星轮啮合齿面均出现了偏载现象，即齿面载荷主要集中在齿轮上风向端面。

齿面载荷分布与啮合齿轮振动位移密切相关。基于推导的式（3）和式（4）可知，太阳轮、行星轮与内齿圈轮齿节点的平移振动会均匀投影至各自对应的啮合线接触点上，而各构件扭转振动会明显改变啮合线接触点的相对位移，容易造成齿面偏载。因此，在不同工况下对比了太阳轮、行星轮和内齿圈轮齿节点的扭转振动位移，如图12所示。

从图12中可知，随着输入扭矩增大，各构件径向扭转振动位移幅值显著增大，并且在时变啮合刚度激励下，各构件径向扭转振动位移出现了周期性波动。内齿圈轮齿节点1径向扭转振动位移出现了低频波动与高频振动，前者主要是由于5个行星轮依次与内齿圈轮齿节点进行啮合，产生了挤压变形。当输入扭矩达到额定值时，行星轮绕θxp1轴和θyp1轴产生了明显的径向扭转变形，均值分别约为-115.62 rad、-41.13 rad，表明行星轮发生了明显的摆动现象。其主要原因是齿轮存在变位系数，使得太阳轮-行星轮、内齿圈-行星轮之间的啮合角并不相等，同时斜齿轮存在螺旋角且两者啮合存在相位差，综合造成太阳轮-行星轮、内齿圈-行星轮动态啮合力的轴向分力分别在θxp1轴和θyp1轴上所形成的合弯矩并非为零。

由于行星轮与销轴之间通过线性弹簧-阻尼单元连接，且在建模时考虑了行星轮几何结构尺寸与销轴之间的作用力关系（图4），使得行星轮径向扭转振动位移与销轴径向变形密切相关，因此提取了不同工况下销轴上、下风向节点的径向振动位移，如图13所示，行星轮系变形如图14所示（Tin=4×106N·m，θ·zc=2 rad/s）。

从图13和图14中可知，相比于销轴x向（径向），销轴y向（切向）变形更加明显，其主要原因是y向主要承担输入扭矩分解后的切向力（图14a）；销轴下风向节点的x、y向振动位移明显大于上风向节点，且随着输入扭矩的增大，差异愈加明显。其主要原因是销轴下风向节点类似于“悬臂梁”结构的自由端，即使销轴上、下风向节点在相同的载荷条件下，下风向节点也会产生更大的结构变形（图14b）。

分析结果表明，造成斜齿轮啮合偏载的主要原因包括太阳轮-行星轮、内齿圈-行星轮斜齿轮啮合产生的轴向分力所形成的合弯矩；行星架销轴上、下风向节点承载时产生了非对称结构变形。

5.3 动态位移对啮合特性影响

动态啮合力可以直接反映系统振动情况。图15所示为转速对行星轮系动态啮合力（有效值且去除均值）影响（Tin=4×106 N·m）。从图中可知，随着输入转速（θ·zc）增大，行星轮系动态啮合力幅值逐渐增大；输入转速约为60 rad/s时产生了共振，动态啮合力幅值达到最大，意味着啮合齿轮振动位移显著增大；随着输入转速的继续增大，动态啮合力幅值开始降低。为了探究啮合齿轮动态位移对齿轮啮合特性影响，对比了不同输入转速下齿轮时变啮合刚度与齿面载荷分布情况，分别如图16和图17所示（Tin=4×106 N·m）。

从图16中可知，当θ·zc为60 rad/s、80 rad/s时，太阳轮-行星轮啮合刚度出现了明显的非规则性波动，尤其是在共振转速附近时，其波动更加明显；内齿圈-行星轮啮合刚度对输入转速变化不敏感，其主要原因是柔性内齿圈的吸振作用。从图17中可知，输入转速变化会改变齿面载荷分布，当系统产生共振时，太阳轮-行星轮、内齿圈-行星轮齿面载荷最大值分别达9615 N、7418 N（图17a），相比于θ·zc=80 rad/s时齿面载荷最大值，分别增大了13.70%、10.75%。

分析结果表明，齿轮啮合刚度并非独立于系统响应，输入转速变化会通过影响各构件振动位移，改变轮齿动态接触状态，影响齿轮啮合刚度（式（13）），并反馈影响各构件动态响应；系统共振会加剧啮合偏载程度。

5.4 行星架柔性对啮合特性影响

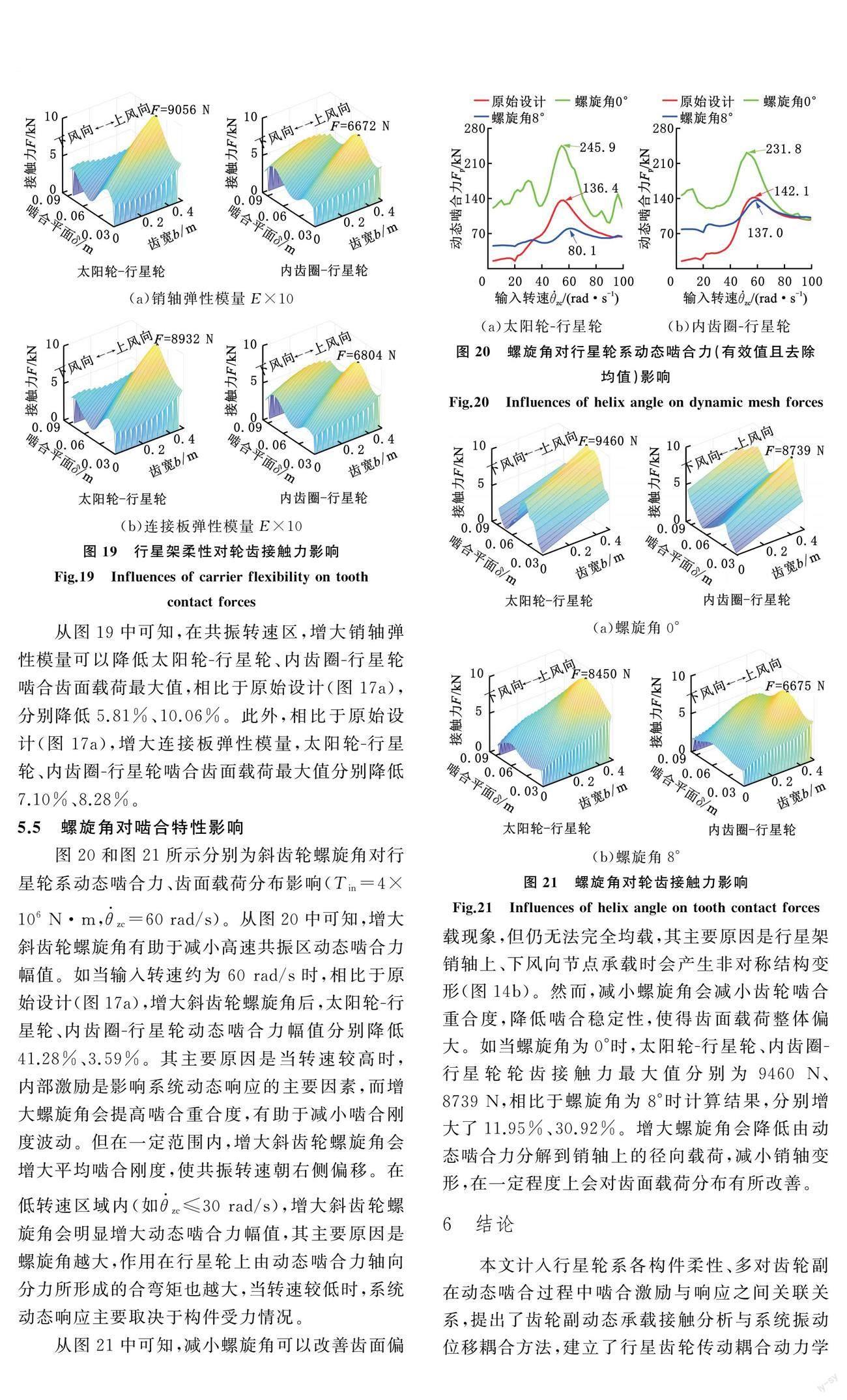
图18和图19所示分别为行星架连接板与销轴弹性模量对行星轮系动态啮合力、齿面载荷分布的影响。其中，连接板与销轴弹性模量设计值均为E=1.06×1011Pa，Tin=4×106 N·m，θ·zc=60 rad/s。

从图18中可知，在共振转速区，增大连接板与销轴弹性模量均可以降低动态啮合力峰值。然而，在低转速区（θ·zc≤30 rad/s），增大销轴弹性模量反而会增大行星轮系动态啮合力波动。

从图19中可知，在共振转速区，增大销轴弹性模量可以降低太阳轮-行星轮、内齿圈-行星轮啮合齿面载荷最大值，相比于原始设计（图17a），分别降低5.81%、10.06%。此外，相比于原始设计（图17a），增大连接板弹性模量，太阳轮-行星轮、内齿圈-行星轮啮合齿面载荷最大值分别降低7.10%、8.28%。

5.5 螺旋角对啮合特性影响

图20和图21所示分别为斜齿轮螺旋角对行星轮系动态啮合力、齿面载荷分布影响（Tin=4×106 N·m，θ·zc=60 rad/s）。从图20中可知，增大斜齿轮螺旋角有助于减小高速共振区动态啮合力幅值。如当输入转速约为60 rad/s时，相比于原始设计（图17a），增大斜齿轮螺旋角后，太阳輪-行星轮、内齿圈-行星轮动态啮合力幅值分别降低41.28%、3.59%。其主要原因是当转速较高时，内部激励是影响系统动态响应的主要因素，而增大螺旋角会提高啮合重合度，有助于减小啮合刚度波动。但在一定范围内，增大斜齿轮螺旋角会增大平均啮合刚度，使共振转速朝右侧偏移。在低转速区域内（如θ·zc≤30 rad/s），增大斜齿轮螺旋角会明显增大动态啮合力幅值，其主要原因是螺旋角越大，作用在行星轮上由动态啮合力轴向分力所形成的合弯矩也越大，当转速较低时，系统动态响应主要取决于构件受力情况。

從图21中可知，减小螺旋角可以改善齿面偏载现象，但仍无法完全均载，其主要原因是行星架销轴上、下风向节点承载时会产生非对称结构变形（图14b）。然而，减小螺旋角会减小齿轮啮合重合度，降低啮合稳定性，使得齿面载荷整体偏大。如当螺旋角为0°时，太阳轮-行星轮、内齿圈-行星轮轮齿接触力最大值分别为9460 N、8739 N，相比于螺旋角为8°时计算结果，分别增大了11.95%、30.92%。增大螺旋角会降低由动态啮合力分解到销轴上的径向载荷，减小销轴变形，在一定程度上会对齿面载荷分布有所改善。

6 结论

本文计入行星轮系各构件柔性、多对齿轮副在动态啮合过程中啮合激励与响应之间关联关系，提出了齿轮副动态承载接触分析与系统振动位移耦合方法，建立了行星齿轮传动耦合动力学模型，形成了“啮合激励-系统振动-反馈影响”相闭环的行星轮系动力学分析流程，分析了啮合偏载现象以及结构参数对啮合特性影响，主要结论如下：

（1）行星轮系斜齿轮啮合会出现齿面偏载现象；动态啮合力在行星轮上产生的轴向分力所形成的合弯矩，以及行星架销轴承载时产生的非对称结构变形是造成齿面偏载的主要原因；系统共振会加剧齿面偏载程度。

（2）齿面瞬时接触特性与系统振动响应之间存在相互影响，系统振动位移会反馈影响齿轮动态啮合刚度；在共振区附近时，齿轮动态啮合刚度与静态啮合刚度会存在较大差异。

（3）增加销轴刚性、增大螺旋角均可以改善齿面偏载状态，降低共振区系统振动，但在低转速区不利于系统减振；增加行星架连接板刚性可以保持低转速区系统振动状态，同时降低共振区系统振动。

参考文献：

［1］ ABOUSLEIMAN V， VELEX P. A Hybrid 3D Finite Element/Lumped Parameter Model for Quasi-Static and Dynamic Analyses of Planetary/Epicyclic Gear Sets［J］. Mechanism and Machine Theory， 2006， 41（6）：725-748.

［2］ ZHANG C， WEI J， WANG F， et al. Dynamic Model and Load Sharing Performance of Planetary Gear System with Journal Bearing［J］. Mechanism and Machine Theory， 2020， 151：103898.

［3］ 许华超， 秦大同. 内激励下弹性边界柔性直齿内齿圈振动响应研究［J］. 机械工程学报， 2018， 54（9）：161-167.

XU Huachao， QIN Datong. Vibration Response of Flexible Spur Ring Gear with Elastic Foundation under Internal Excitation［J］. Journal of Mechanical Engineering， 2018， 54（9）：161-167.

［4］ 张俊， 宋轶民， 王建军. 计入齿圈柔性的直齿行星传动动力学建模［J］. 机械工程学报， 2009， 45（12）：29-36.

ZHANG Jun， SONG Yimin， WANG Jianjun. Dynamic Modeling for Spur Planetary Gear Transmission with Flexible Ring Gear［J］. Journal of Mechanical Engineering， 2009， 45（12）：29-36.

［5］ 刘向阳， 周建星， 章翔峰， 等. 考虑齿圈柔性的风电机组行星传动均载特性与灵敏度分析［J］. 太阳能学报， 2021， 42（7）：340-349.

LIU Xiangyang， ZHOU Jianxing， ZHANG Xiangfeng， et al. Analysis of Load Sharing Characteristics and Sensitivity of Planetary Transmission of Wind Turbine Considering Flexibility of Gear Ring［J］. Acta Enerciae Solaris Sinica， 2021， 42（7）：340-349.

［6］ SAADA A， VELEX P. An Extended Model for the Analysis of the Dynamic Behavior of Planetary Trains［J］. Journal of Mechanical Design， 1995， 117（2A）：241-247.

［7］ VELEX P， MAATAR M. A Mathematical Model for Analyzing the Influence of Shape Deviations and Mounting Errors on Gear Dynamic Behaviour［J］. Journal of Sound and Vibration， 1996， 191（5）：629-660.

［8］ RACLOT J P， VELEX P. Simulation of the Dynamic Behaviour of Single and Multi-stage Geared Systems with Shape Deviations and Mounting Errors by Using a Spectral Method［J］. Journal of Sound and Vibration， 1999， 220（5）：861-903.

［9］ LIU C， QIN D， LIAO Y. Dynamic Model of Variable Speed Process for Herringbone Gears Including Friction Calculated by Variable Friction Coefficient［J］. Journal of Mechanical Design， 2014， 136（4）：041006.

［10］ YOUNES E B， CHANGENET C， BRUYERE J， et al. Multi-objective Optimization of Gear Unit Design to Improve Efficiency and Transmission Error［J］. Mechanism and Machine Theory， 2022， 167：104499.

［11］ CHAPRON M， VELEX P， BRUYRE J， et al. Optimization of Profile Modifications with Regard to Dynamic Tooth Loads in Single and Double-helical Planetary Gears with Flexible Ring-gears［J］. Journal of Mechanical Design， 2016， 138（2）：023301.

［12］ AJMI M， VELEX P. A Model for Simulating the Quasi-static and Dynamic Behaviour of Solid Wide-faced Spur and Helical Gears［J］. Mechanism and Machine Theory， 2005， 40（2）：173-190.

［13］ GUILBERT B， VELEX P， DUREISSEIX D， et al. Modular Hybrid Models to Simulate the Static and Dynamic Behaviour of High-speed Thin-rimmed Gears［J］. Journal of Sound and Vibration， 2019， 438：353-380.

［14］ 白恩軍， 谢里阳， 佟安时， 等. 考虑齿轮轴变形的斜齿轮接触分析［J］. 兵工学报， 2015， 36（10）：1975-1981.

BAI Enjun， XIE Liyang， TONG Anshi， et al. The Contact Analysis of Helical Gear in Considering Gear Shaft Deformation［J］. Acta Armamentarii， 2015， 36（10）：1975-1981.

［15］ 袁冰， 常山， 刘更， 等. 大齿宽齿轮耦合转子系统准静态接触分析及动态特性［J］. 机械工程学报， 2020， 56（3）：96-105.

YUAN Bing， CHANG Shan， LIU Geng， et al. Quasi-static Contact and Dynamic Behaviors Analysis of Wide-faced Gear Coupled with Rotor System［J］. Journal of Mechanical Engineering， 2020， 56（3）：96-105.

［16］ 王涛， 唐增宝. 齿轮传动的动态啮合刚度［J］. 华中理工大学学报， 1992， 20（3）：39-44.

WANG Tao， TANG Zengbao. The Dynamic Meshing Stiffness of Gear Transmission［J］. Journal of Huazhong University of Science and Technology， 1992， 20（3）：39-44.

［17］ CAI Y， HAYASHI T. The Linear Approximated Equation of Vibration of a Pair of Spur Gears Theory and Experiment［J］. Journal of Mechnical Design， 1994， 20（3）：558-564.

［18］ MATSUMURA S， UMEZAWA K， HOUJOH H. Rotational Vibration of a Helical Gear Pair Having Tooth Surface Deviation during Transmission of Light Load［J］. JSME International Journal. Ser. C， Dynamics， Control， Robotics， Design and Manufacturing， 1996， 39（3）：614-620.

［19］ CAO Z， CHEN Z， JIANG H. Nonlinear Dynamics of a Spur Gear Pair with Force-dependent Mesh Stiffness［J］. Nonlinear Dynamics， 2020， 99：1227-1241.

［20］ PARKER R G， VIJAYAKAR S M， IMAJO T. Non-linear Dynamic Response of a Spur Gear Pair：Modelling and Experimental Comparisons［J］. Journal of Sound and Vibration， 2000， 237（3）：435-455.

［21］ ZHANG C， DONG H， WANG D， et al. A New Effective Mesh Stiffness Calculation Method with Accurate Contact Deformation Model for Spur and Helical Gear Pairs［J］. Mechanism and Machine Theory， 2022， 171：104762.

［22］ 赵百顺， 李娜， 马辉， 等. 混合修形斜齒轮转子系统振动特性分析［J］. 振动工程学报， 2021， 34（4）：704-711.

ZHAO Baishun， LI Na， MA Hui， et al. Vibration Characteristics of the Helical Gear Rotor System Considering Mixed Modification［J］. Journal of Vibration Engineering， 2021， 34（4）：704-711.

［23］ 常乐浩， 田宏炜， 贺朝霞， 等. 结合有限元法和接触理论的内齿轮副啮合刚度计算方法［J］. 机械传动， 2018， 42（8）：61-64.

CHANG Lehao， TIAN Hongwei， HE Zhaoxia， et al. A Method for Determining the Mesh Stiffness of Internal Gearby Combining Finite Element Method and Contact Theory［J］. Mechanical Transmission， 2018， 42（8）：61-64.

［24］ TAN Jianjun， LI Hao， TANG Hao， et al. Dynamic Modeling and Analysis of Planetary Gear Train System Considering Structural Flexibility and Dynamic Multi-teeth Mesh Process［J］. Mechanism and Machine Theory， 2023， 186：105348.

［25］ HELSEN J， VANHOLLEBEKE F， MARRANT B， et al. Multibody Modelling of Varying Complexity for Modal Behaviour Analysis of Wind Turbine Gearboxes［J］. Renewable Energy， 2011， 36（11）：3098-3113.

［26］ WANG J. Rayleigh Coefficients for Series Infrastructure Systems with Multiple Damping Properties［J］. Journal of Vibration and Control， 2015， 21（6）：1234-1248.

［27］ TAN J， ZHU C， SONG C， et al. Dynamic Modeling and Analysis of Wind Turbine Drivetrain Considering Platform Motion［J］. Mechanism and Machine Theory， 2019， 140：781-808.

［28］ CHEN K， MA H， CHE L， et al. Comparison of Meshing Characteristics of Helical Gears with Spalling Fault Using Analytical and Finite-element Methods［J］. Mechanical Systems and Signal Processing， 2019， 121：279-298.

［29］ NATALI C， BATTARRA M， DALPIAZ G， et al. A Critical Review on FE-based Methods for Mesh Stiffness Estimation in Spur Gears［J］. Mechanism and Machine Theory， 2021， 161：104319.

［30］ WAN X， ZHI Q. Precise Integration Method for LQG Optimal Measurement Feedback Control Problem［J］. Applied Mathematics and Mechanics， 2000， 21：1417-1422.

（编辑 王旻玥）

作者简介：

谭建军，男，1991年生，副研究员。研究方向为齿轮传动系统动力学、减振优化。E-mail：jianjuntan@cqu.edu.cn。