变速箱中间轴焊接结构多轴疲劳寿命分析方法

曹蕾蕾 康凡军 郭城臣 宋绪丁 吕文彻

摘要：

重載车辆传动系统具有大速比、大扭矩的特点，其变速箱中间轴焊接结构承受复杂工作载荷，焊缝处易发生多轴疲劳破坏。为了更准确有效地对中间轴焊接结构的疲劳寿命进行评估，基于多轴结构应力法提出一种重载车辆变速箱中间轴焊接结构疲劳寿命分析方法，即建立含有焊缝细节的中间轴焊接结构有限元模型，求解得到焊缝危险点处的结构应力分量时间历程，并在结构应力平面上合成载荷路径，求得非比例加载路径的等效应力范围，最后结合主S-N曲线确定焊接结构的疲劳寿命。采用该方法分别对中间轴焊接结构的焊根、焊趾部位进行疲劳寿命分析并与疲劳台架试验结果进行对比，结果表明：分析得到的疲劳破坏位置和寿命值与疲劳台架试验结果均有良好的一致性，且焊根与焊趾寿命分析结果间的差异与已有文献多轴疲劳试验数据相一致，说明采用多轴结构应力法对变速箱中间轴焊接结构的疲劳寿命评估是可靠的。

关键词：变速箱中间轴；焊接结构；多轴疲劳；多轴结构应力法；非比例载荷路径

中图分类号：TG405

DOI：10.3969/j.issn.1004-132X.2023.13.010

Multi-axis Fatigue Life Analysis Method for Welded Structures of Transmission Intermediate Shafts

CAO Leilei1，2 KANG Fanjun1 GUO Chengchen1 SONG Xuding1 LYU Wenche2

1.Key Laboratory of Road Construction Technology and Equipment of the Ministry of Education，Changan University，Xian，710064

2.Shaanxi Provincial Key Laboratory of Gear Transmission，Shaanxi Fast Gear Co.，Ltd.，Xian，710119

Abstract： The transmission system of heavy-duty vehicles had the characteristics of large speed ratio and large torque. The welded structures of transmission intermediate shafts carried complex working loads， and multiaxial fatigue failure was easy to occur at the weld seams. In order to evaluate the fatigue life more accurately and effectively， a fatigue life analysis method for the welded structures of transmission intermediate shafts of heavy-duty vehicles was proposed based on the multi-axial structural stress method. First， the finite element model with weld details for the welded structures of transmission intermediate shafts was built. Then， the time history of the structural stress components at the fatigue hazard points of the welds was solved， the load path was synthesized on the structural stress planes to obtain the equivalent stress range of the non-proportional loading path. Finally， the fatigue life was determined by combining the main S-N curve. This method was used to evaluate the fatigue life of the weld roots and weld toes of the welded structures of transmission intermediate shafts， and the results were compared with those of the fatigue bench tests. Results show that the predicted damage location and fatigue life are both in good agreement with the experiments， and the differences between the fatigue life of the weld roots and toes are consistent with the multi-axial fatigue test results in the existing literature， which indicating that the proposed multi-axial structural stress method is reliable for the fatigue life assessment of the welded structures of transmission intermediate shafts.

Key words： transmission intermediate shaft； welded structure； multi-axial fatigue； multi-axial structural stress method； non-proportional load path

收稿日期：2022-11-07

基金项目：

中央高校基本科研业务费专项资金（300102252101）；广西制造系统与先进制造技术重点实验室开放基金（22354S010）；陕西省自然科学基金（2021JM166）

0 引言

重载车辆在基础建设、物流运输等领域发挥着关键作用，因其行驶环境十分恶劣，变速箱需满足大速比、大扭矩的要求。变速箱负载峰值高、波动大，其中间轴结构承受复杂多轴疲劳载荷，其疲劳损伤行为影响着变速箱性能和重载汽车的服役安全。

目前，单轴疲劳研究已形成较为成熟的疲劳损伤评估和寿命预测方法，但多轴疲劳问题，尤其是多轴非比例加载疲劳问题的研究尚未形成体系［1］。目前多轴疲劳失效评估的常用做法是将复杂多轴应力状态等效为一个标量值，再基于单轴疲劳评估进行疲勞寿命预测。已建立的多轴高周疲劳评估准则有应力不变准则、临界面准则和等效应力准则［2］。其中，应力不变准则使用简单，适用于比例加载情况，可预测裂纹是否萌生，但无法预测疲劳开裂的位置，具有局限性。临界面准则能够较好地反映裂纹形核平面，得到了广泛应用［3］，然而，其疲劳评估结果因临界面与应力类型的选取不同会存在较大差异。近年来，DONG等［4-7］将等效结构应力法拓展到多轴疲劳领域，提出多轴结构应力法［8-9］。该方法在结构应力的基础上，考虑多轴疲劳损伤中材料与载荷路径对结构疲劳损伤的影响，采用一条主S-N曲线将各种接头类型、板厚、加载模式纳入到统一标准中进行评估，可同时适用于比例和非比例加载，并具有网格不敏感性，引起了国内外学者的关注［9］。目前，多轴结构应力法已经应用在轨道车辆转向架焊接结构［10］、造船龙门起重机焊接结构［11］的疲劳寿命评估中，取得了较好的研究成果，但以上研究尚未与疲劳台架试验结果进行对比验证。

本文针对变速箱中间轴结构在复杂工况下的焊缝疲劳破坏问题，基于变速箱加速疲劳试验的强化载荷谱，对中间轴焊接结构的疲劳寿命进行研究，即基于多轴结构应力法提出一种重载车辆变速箱中间轴焊接结构疲劳寿命评估方法，建立中间轴焊接结构多轴疲劳寿命评估模型，并对其焊根、焊趾部位分别进行评估，将评估结果与台架疲劳试验结果进行对比分析。

1 多轴结构应力法

在多轴载荷作用下，焊接结构焊缝区域贯穿板厚方向的切面上存在着多个应力分量的共同作用，如图1所示。

各结构应力分量分别如下［12］：

σs=σm+σb=fy′d－6mx′d2

τs=τm+τb=fx′d－6my′d2

τs′=fz′d（1）

式中，σs为法向正结构应力分量；τs为面内剪切结构应力分量；τs′为面外剪切结构应力分量；（σm；τm）为膜应力；σb为弯曲应力；τb为剪切应力；（fx′，fy′，fz′）为线力；（mx′，my′）为线力矩；d为母材板厚。

大量多轴疲劳试验结果表明，多轴疲劳损伤主要由法向正结构应力分量σs与面内剪切结构应力分量τs造成，因此，为计算方便，面外剪切结构应力分量τs′可以忽略不计［13］。

1.1 多轴加载条件下的等效应力计算

对于多轴比例加载情况，各应力分量同相位、成比例，故多轴有效应力范围Δσe可通过法向结构应力范围Δσs与面内剪切结构应力范围Δτs线性叠加进行计算，并以此作为等效应力范围，如下所示：

Δσe=（Δσs）2+β（Δτs）2（2）

式中，β为材料参数，表征材料疲劳试验中法向应力与剪切应力的疲劳强度之比，钢材的β值取3。

多轴非比例加载情况下，各应力分量随时间独立变化，故需要考虑载荷路径对结构疲劳损伤的影响。采用路径依赖最大范围法（path-dependent maximum range，PDMR）［8］对各多轴应力分量进行周期循环计数，对载荷路径上每个半周期内的最大有效应力范围Δσ（i）e和实际累积载荷路径应力范围ΔS（i）e进行统计，再利用载荷路径力矩法（moment of load path，MLP）［9］对载荷路径的非比例程度进行量化，即定义非比例度gNP：

gNP=DNPDmax=∫AB～r′sinθds′∫AB～Rsinθds′=∫AB～r′sinθds′2R2（3）

式中，载荷路径位于极坐标系（r′，θ）中，极点为比例加载路径中点，极轴为比例加载路径所在直线；ds′表示对弧长积分；DNP为非比例加载路径偏离比例加载路径引起的疲劳损伤；Dmax表示应力分量相位差为90°的最大疲劳损伤；R为Dmax对应的最大极径；gNP的取值范围为0～1，当沿比例加载路径加载时，gNP=0；沿非比例半圆形加载路径加载时，gNP=1。

在得到非比例度的基础上可得到非比例加载路径下的等效应力范围ΔσNP：

ΔσNP=Δσe（1+αgNP）（4）

式中，α为材料敏感度系数，其值可以通过材料疲劳试验进行测定，结构钢α为1［9］。

由式（4）可以看出，等效应力范围ΔσNP同时考虑了载荷路径和材料对多轴疲劳损伤的影响。

1.2 多轴等效结构应力与主S-N曲线

根据计算出的多轴等效应力范围ΔσNP（比例加载退化为Δσe），结合板厚d、弯曲比r等相关参数即可求解多轴应力状态下的等效结构应力范围ΔSNP［12］：

ΔSNP=ΔσNPd（2－k）/（2k）I（r）1/k（5）

式中，ΔSNP为多轴等效结构应力范围；I（r）为载荷弯曲比r的量纲一常数；k为长裂纹扩展指数。

再结合主S-N曲线对焊接结构的疲劳寿命进行评估：

N=（ΔSNP/Cd）－1h（6）

式中，Cd为与材料、应力比等有关的参数；h为常数；N为循环次数。

Cd和h的选取见文献［14］。

2 中间轴焊接结构多轴疲劳寿命评估

2.1 中间轴结构有限元模型建立及分析

为满足重载车辆大速比、大扭矩等复杂工况的要求且同时保证传动精度，本文研究的某型重载车辆变速箱中间轴与齿轮过盈配合，在轴肩二者结合部位焊接加固。在实际工作过程中发现其焊缝区域易发生疲劳破坏。根据中间轴实际结构建立考虑焊缝细节的有限元模型。采用Solid185单元在Hypermesh中进行网格划分，其中，结构区域采用网格尺寸为3 mm的四面体单元，焊缝区域采用网格尺寸为1 mm的六面体单元进行局部网格加密。模型共1 535 040个单元，1 150 274个节点。中间轴结构为20CrNiMo合金结构钢，屈服强度为785 MPa，弹性模量为208 kN/mm2，泊松比为0.31。

边界条件的施加应能够模拟中间轴实际工作时所受的约束和载荷特点。中间轴结构有限元模型的边界条件包括约束边界条件、接触边界条件和载荷边界条件。在实际装配中，采用轴承支撑将中间轴固定在变速箱体中，约束中间轴与轴承装配面的径向自由度，防止中间轴结构的径向跳动，并保留其轴向的转动自由度以模拟中间轴在轴承中的转动；限制中间轴端面的轴向平动自由度，防止中间轴的轴向窜动。在齿轮安装孔内表面与中间轴外表面设置摩擦接触对，并根据实际装配公差范围设置接触对间的过盈量为0.047 mm以模拟过盈配合。轴肩配合处采用节点耦合模拟焊接连接，即中间轴与焊缝共节点、焊缝与齿轮共节点，而齿轮与中间轴之间无节点耦合。焊接区域接触条件施加位置见图2a所示的沿轴线半剖视图。本研究基于重载车辆变速箱加速疲劳试验进行，所采用的强化试验载荷谱如表1所示。在进行各挡位有限元分析时，将载荷谱扭矩转化为径向力、轴向力和圆周力，将相应载荷分别施加在驱动齿轮和减速齿轮上，载荷施加沿着齿面与分度圆重合处的齿宽线均匀加载。最终建立的中间轴结构有限元模型如图2b所示。

在ANSYS软件中对有限元模型进行求解，可得各挡位工况下中间轴结构的von Mises应力云图，此处以3挡载荷工况为例，如图3所示。

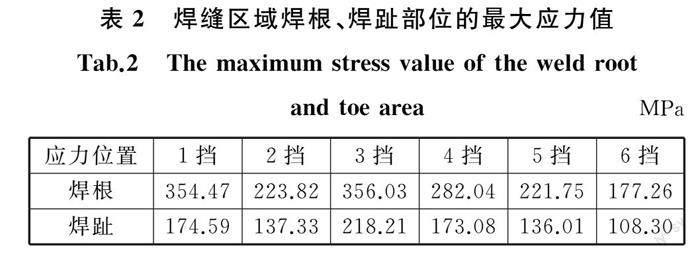
由图3a可知，轮齿载荷施加部位以及焊缝部位的应力值较大，经校核轮齿强度满足设计要求。焊缝剖面应力云图见图3b，可以看出焊根应力远大于焊趾应力。各挡位载荷作用下，焊缝区域焊根、焊趾部位的最大应力值汇总于表2中。结果表明，在循环载荷作用下，中间轴结构焊根部位首先发生疲劳破坏。

2.2 基于多轴结构应力法的疲劳寿命评估

基于以上有限元求解结果，以3挡为例，对中间轴结构进行疲劳评估。提取焊根区域的节点力，计算焊根危险点处的结构应力分量［12］，它随时间变化的情况如图4所示。

由图4可以看出，变速箱中间轴结构疲劳破坏点承受结构正应力与结构剪切应力，为图1所示的多轴应力状态，且其结构正应力分量和结构剪切应力分量随时间各自独立变化，为非比例加载。在結构应力平面（σs，3τs）上对结构应力分量-时间历程进行载荷路径合成，结果如5a所示。

图5中A、B两点的直线距离即为载荷路径的最大结构应力变化范围Δσe。基于PDMR法对载荷路径进行周期计数，从A点出发沿载荷路径瞬时净距离逐渐增大，到达B点后减小，则令第一个半周期的载荷路径为曲线AB～，如图5b所示。第一次计数完成以后，删除已统计过的路径，继续对剩余路径进行循环计数，第二个半周期的载荷路径为曲线BA～，如图5c所示。所有载荷路径统计完成，计数结果统计于表3。

在PDMR法计数的基础上，进行载荷路径非比例度的计算。图6为第一个半周期载荷路径的非比例度求解示意图。

在图6中，以直线AB——比例加载的中点为原点，以AB——所在直线为x′轴，建立局部坐标系x′-y′，由图6可得，r′sinθ=y′，ds′=（dx′）2+（dy′）2，根据式（3），有

gNP=∫AB～r′sinθds′2R2=∫AB～y′（dx′）2+（dy′）22R2（7）

在非比例度计算的基础上，可得到一个周期的等效应力范围ΔσNP：

ΔσNP=Δσe［1+α（gNP1+gNP2）］（8）

式中，gNP1、gNP2分别为第一、二个半周期载荷路径的非比例度。

根据计算出的各挡位载荷作用下的等效应力范围ΔσNP，结合板厚、弯曲比等相关参数求解中间轴结构各挡位载荷作用下多轴等效结构应力范围ΔSNP，并根据焊根处主S-N曲线计算得出中间轴结构的疲劳循环次数，进而结合变速箱台架疲劳试验谱得出各挡位循环载荷作用下的疲劳损伤比，结果汇总于表4。由表4可以看出，不同挡位的载荷具有相同的非比例度，其原因在于不同挡位虽扭矩不同，而有限元应力结果与扭矩成比例关系，故其量纲一非比例度为定值。

由表4结果结合Miner线性累积损伤准则［15-16］计算累积疲劳损伤值：

L=∑ki=1niNi（9）

式中，ni、Ni为第i级载荷对应的试验循环次数和疲劳失效循环次数；L为累计疲劳损伤值。

根据式（9）计算得到中间轴焊接结构焊根部位的累计损失值为0.030 134 258，表1疲劳试验中一个载荷谱块的等效时间为94.8722 min，故焊根部位的疲劳寿命为52.47 h。采用相同方法并结合焊趾处的主S-N曲线，可对焊趾部位进行多轴疲劳寿命评估。表5为焊缝各部位疲劳寿命评估结果汇总。

從表5中可以看出，焊根处的预测寿命为52.5 h，焊趾处为110.5 h。焊根处的疲劳寿命远远低于焊趾处，二者数值相差大约50%，与目前公开发表的焊根、焊趾处多轴疲劳试验数据的差值范围一致［17］。

3 试验验证与讨论

为了验证该疲劳评估结果的有效性，采用表1所示强化载荷谱对变速箱进行加速台架疲劳试验，疲劳试验装置如图7所示。疲劳试验加载30个谱块即47.44 h后，中间轴结构焊缝处发生断轴现象，如图8a所示，焊缝局部放大图见图8b。由图可以看出，焊缝中部区域首先发生疲劳破坏，而焊趾处并未发现宏观裂纹。焊缝区域的X光透射照片见图8c，可以发现疲劳破坏首先发生在焊根部位，并沿焊喉方向在焊缝中部开裂，因此焊根部位疲劳破坏是造成中间轴结构疲劳失效的主要因素，该结论与有限元仿真结果吻合。

多轴疲劳寿命评估结果与台架疲劳试验结果对比情况如表6所示。由表6可以得出，焊根处的疲劳寿命评估结果与台架疲劳试验结果相吻合，验证了疲劳评估结果的准确性，表明采用多轴结构应力法的相关准则对重载车辆变速箱中间轴焊接结构进行多轴疲劳寿命评估是有效可靠的。

4 结论

（1）本文根据中间轴结构实际工况和受载情况建立了带有焊缝细节的有限元模型，通过有限元分析得到焊根部位是中间轴结构在各挡位循环载荷作用下的疲劳薄弱点，该位置与台架疲劳试验破坏位置一致。

（2）采用多轴结构应力法建立了中间轴焊接结构疲劳寿命评估模型，并结合台架疲劳试验谱对中间轴结构焊根、焊趾部位分别进行了疲劳寿命评估。其中，焊根部位疲劳评估寿命为52.5 h，焊趾部位疲劳评估寿命为110.5 h，二者疲劳寿命的差值接近50%，与公开发表的焊根、焊趾处多轴疲劳试验数据的差值范围一致；

（3）基于多轴结构应力法的疲劳寿命评估方法综合考虑了多轴疲劳破坏中载荷路径及材料对结构疲劳损伤的影响，可应用于非比例加载情况，评估结果有效可靠。该方法可为其他焊接结构的多轴疲劳寿命评估提供新的思路。

参考文献：

［1］ 赵而年， 瞿伟廉， 周强. 基于临界面损伤参量的金属材料多轴疲劳寿命预测［J］. 华南理工大学学报（自然科学版）， 2017， 45（2）：130-136.

ZHAO Ernian， QU Weilian， ZHOU Qiang. Multiaxial Fatigue Life Prediction of Metallic Materials Based on Critical Plane Damage Parameter［J］. Journal of South China University of Technology（Natural Science）， 2017， 45（2）：130-136.

［2］ PAPUGA J. A Survey on Evaluating the Fatigue Limit under Multiaxial Loading［J］. International Journal of Fatigue， 2011， 33（2）：153-165.

［3］ 孙国芹， 尚德广， 王杨. 金属多轴疲劳行为与寿命预测研究进展［J］. 机械工程学报， 2021， 57（16）：153-172.

SUN Guoqin， SHANG Deguang， WANG Yang. Research Progress on Fatigue Behavior and Life Prediction under Multiaxial Loading for Metals［J］. Journal of Mechanical Engineering， 2021， 57（16）：153-172.

［4］ DONG P. A Structural Stress Definition and Numerical Implementation for Fatigue Analysis of Welded Joints［J］. International Journal of Fatigue， 2001， 23：865-876.

［5］ DONG P. A Robust Structural Stress Method for Fatigue Analysis of Offshore/Marine Structures［J］. Journal of Offshore Mechanics and Arctic Engineering， 2005， 127（1）：68-74.

［6］ DONG P， HONG J K. The Master S-N Curve Approach to Fatigue Evaluation of Offshore and Marine Structures［C］∥ ASME 2004 23rd International Conference on Offshore Mechanics and Arctic Engineering. Vancouver， 2004：847-855.

［7］ DONG P， HONG J K. Analysis of Recent Fatigue Data Using the Structural Stress Procedure in ASME Div 2 Rewrite［J］. Journal of Pressure Vessel Technology， 2007， 129（3）：355-362.

［8］ DONG P， WEI Z， HONG J K. A Path-dependent Cycle Counting Method for Variable-amplitude Multi-axial Loading［J］. International Journal of Fatigue， 2010， 32（4）：720-734.

［9］  MEI J， DONG P. A New Path-dependent Fatigue Damage Model for Non-proportional Multi-axial Loading［J］. International Journal of Fatigue， 2016， 90：210-221.

［10］ 周民浩. 轨道车辆转向架构架的静强度仿真及多轴疲劳分析［D］. 大连：大连交通大学， 2020.

ZHOU Minhao. Static Analysis and Multiaxial Fatigue Analysis of Railway Vehicles Bogie Frame［D］. Dalian：Dalian Jiaotong University， 2020.

［11］ 岳增可. 造船龙门起重机焊接结构多轴疲劳寿命研究［D］. 大连：大连理工大学， 2021.

YUE Zengke. Research on Multi-axial Fatigue Life of Welded Structure of Shipbuilding Gantry Crane［D］. Dalian：Dalian University of Technology， 2021.

［12］ 曹蕾蕾， 王留涛， 王严， 等. 基于等效结构应力法的挖掘机工作装置疲劳寿命评估［J］. 华南理工大学学报（自然科学版）， 2022， 50（8）：62-70.

CAO Leilei， WANG Liutao， WANG Yan， et al. Fatigue Life Evaluation of Excavator Working Device Based on Equivalent Structural Stress Method［J］. Journal of South China University of Technology（Natural Science）， 2022， 50（8）：62-70.

［13］ 尚德广， 王大康， 孙国芹， 等. 多轴疲劳裂纹扩展行为研究［J］. 机械强度， 2004（4）：423-427.

SHANG Deguang， WANG Dakang， SUN Guoqin， et al. Behavior of Multiaxial Fatigue Crack Propagation［J］. Journal of Mechanical Strength， 2004（4）：423-427.

［14］ 兆文忠， 李向伟， 董平沙. 焊接结构抗疲劳设计理论与方法［M］. 北京：机械工业出版社， 2017.

ZHAO Wenzhong， LI Xiangwei， DONG Pingsha. Theory and Method of Fatigue Resistance Design for Welded Structures［M］. Beijing：China Machine Press， 2017.

［15］ MINER M A. Cumulative Damage in Fatigue［J］. 1945， 12（3）：A159-A164.

［16］ 曹蕾蕾， 郭城臣， 王严， 等. 基于实测数据的挖掘机工作装置疲劳寿命评估［J］. 华南理工大学学报（自然科学版）， 2021， 49（8）：122-128.

CAO Leilei， GUO Chengchen， WANG Yan， et al. Fatigue Analysis of Hydraulic Excavator Working Device Based on Experiment Data［J］. Journal of South China University of Technology（Natural Science）， 2021， 49（8）：122-128.

［17］ HONG J K. Evaluation of Weld Root Failure Using Battelle Structural Stress Method［J］. Journal of Offshore Mechanics and Arctic Engineering， 2013， 135（2）：021404.

（編辑 王旻玥）

作者简介：

曹蕾蕾，女，1983年生，博士，副教授。研究方向为工程机械动态仿真与抗疲劳设计。E-mail：caoleilei@chd.edu.cn。